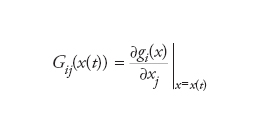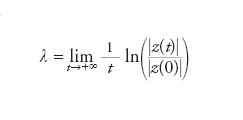esponenti di Lyapunov

esponenti di Lyapunov

Concetto chiave nella generalizzazione dell’analisi di stabilità dei punti fissi e delle orbite periodiche di un sistema dinamico. Gli esponenti di Lyapunov permettono una caratterizzazione quantitativa della dipendenza sensibile dalle condizioni iniziali. Per semplicità di notazione discutiamo il caso di un sistema a tempo discreto x(t+1)=g(x(t)) dove x∈ℝ^ν e g:ℝ^ν→ℝ^ν. Siano x¹(t) e x²(t) due traiettorie (supposte arbitra-riamente vicine): il vettore z(t)=x¹(t)−x²(t), evolve secondo la legge

z(t +1) = G(x(t))z(t), z(t) = A^τz(0)

dove A^τ=G(x(t)G(x(t−1))...G(x(2)G(x(1)) e gli elementi della matrice G sono

Il più grande degli esponenti di Lyapunov è allora definito dalla formula

Il significato intuitivo degli esponenti di Lyapunov è il seguente: λ₁ è il tasso di crescita tipico di una variazione infinitesimale generica, ossia ∣z(t)∣∼expλ₁t, (λ₁+λ₂) è il tasso di crescita tipico dell’area del parallelogrammo individuato da due variazioni infinitesimale generiche, ossia A(t)∼exp(λ₁+λ₂)t. Analoga­mente, λ₁+...+λ_ϰ è il tasso di crescita tipico del volume del parallelogrammo di dimensioni k individuato da k perturbazioni infinitesimali generiche, ossia V_ϰ(t)∼exp(λ₁+...+λ_ϰ)t. Un importante risultato, dovuto a V.I. Oseledec e che rientra nella famiglia dei teoremi ergodici, esplicita il legame tra gli esponenti di Lyapunov e la matrice A^τ. Si considerino infatti la matrice

B^τ = [A^τ (A^τ)^†]^1/2τ

(dove † indica il trasposto coniugato) e i suoi autovalori (in ordine decrescente)

e ^α1, e ^α2, ..., e ^αΝ .

Nel limite t→+∞, α₁, α₂ ... α_Ν sono indipendenti da x(0) e coincidono con gli esponenti di Lyapunov λ₁, ..., λ_Ν. Gli esponenti di Lyapunov, oltre a caratterizzare un sistema dinamico da un punto di vista qualitativo, sono connessi con l’entropia di Kolmogorov-Sinai.

→ Caos deterministico