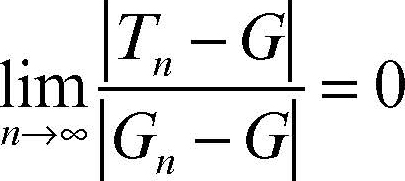estrapolazione al limite
estrapolazione al limite
estrapolazione al limite nel calcolo numerico e in matematica applicata, metodo numerico per la determinazione del valore di una grandezza G a partire da un procedimento, dipendente da un parametro h, che fornisce un’approssimazione G(h) tale che
Per esempio, nell’integrazione numerica, il procedimento iterativo dipende dal parametro h che dà l’ampiezza dei sottointervalli in cui è suddiviso l’intervallo [a, b] su cui si integra. A sua volta, il parametro h, nei successivi passi dell’iterazione, è una successione hn per cui G(h) dipende di fatto da n e si può scrivere Gn = G(hn). Spesso, in pratica, la convergenza di Gn è lenta e occorre accelerarla. A tale scopo la successione Gn viene trasformata, attraverso una trasformazione di successioni T, in una nuova successione Tn che converga allo stesso limite di Gn ma sia più “veloce”, sia tale cioè che:
Per effettuare tale trasformazione nel caso che G sia una grandezza scalare, si assume che Gn si comporti come una funzione R di n dipendente da k + 1 parametri α1, …, αk, g che sono determinati imponendo le condizioni:
in cui g è presa come un’approssimazione del limite G della successione Gn. I parametri α1, …, αk, g, ottenuti come soluzione del sistema (1), dipendono da n. Per tale motivo, g sarà denotato con Tn, che definisce la trasformazione di successioni T: Gn → Tn. Se la successione Sn soddisfa (1) per ogni n, dove g e αi sono costanti indipendenti da n, allora, per costruzione, Tn = g per ogni n. Spesso la condizione è anche necessaria. L’insieme delle successioni che soddisfano questa condizione è anche chiamata nucleo della trasformazione T.