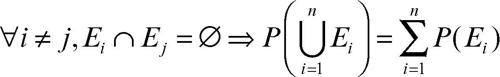evento

evento

evento in probabilità, uno dei possibili risultati di una prova. Una prova definisce un insieme Ω di possibili esiti o casi, mutuamente incompatibili, detti eventi elementari. L’insieme Ω è detto spazio degli eventi o insieme universo o, ancora, spazio campionario, e può essere finito o infinito. Per esempio, nel lancio di un dado lo spazio degli eventi, finito, è {1, 2, 3, 4, 5, 6}; nel lancio di una boccia in un campo da bocce, lo spazio degli eventi, infinito e continuo, è costituito da tutti i punti del rettangolo di gioco (se si esclude che le bocce fuoriescano dal campo). Un evento è un sottoinsieme E dello spazio degli eventi; tra essi sono compresi l’insieme vuoto, indicato con Ø (detto evento impossibile) e lo stesso insieme Ω (detto evento certo). Va sottolineato che in certe particolari condizioni, se Ω è infinito e non numerabile, non tutti i suoi sottoinsiemi sono ammissibili come eventi e si costruisce pertanto la classe degli eventi ammissibili (→ probabilità, assiomi della).

A ciascun evento E ⊆ Ω è assegnata una misura di probabilità indicata con P(E) che, da un punto di vista matematico, è una funzione definita sull’insieme delle parti di Ω, che assume valori reali da 0 a 1, estremi compresi. Si ha:

• P(Ø) = 0 (l’evento impossibile ha probabilità 0);

• P(Ω) = 1 (l’evento certo ha probabilità 1).

Poiché gli eventi sono sottoinsiemi e sono descrivibili attraverso proposizioni, per descrivere le relazioni tra due o più eventi è possibile utilizzare sia i connettivi logici sia le operazioni tra insiemi, sicché, per esempio, dati due eventi A e B si può indicare la loro unione con A ∪ B oppure attraverso la disgiunzione A o B, indicata anche con A ∨ B (una notazione più tradizionale utilizza in questo caso il simbolo dell’addizione: A + B); si può invece indicare la loro intersezione con A ∩ B oppure attraverso la congiunzione A e B, indicata con A ∧ B (una notazione più tradizionale utilizza in questo caso il segno della moltiplicazione A · B oppure A × B o la semplice giustapposizione AB).

In particolare, se il verificarsi di un evento A esclude che possa verificarsi l’evento B, i due eventi sono detti incompatibili o disgiunti e si ha quindi A ∩ B = Ø e P(A ∩ B) = 0. Tale, per esempio nel lancio di un dado, è il caso degli eventi A = {numero minore di 3} e B = {numero maggiore di 4}. Per definizione, gli eventi elementari, poiché sono elementi dell’insieme universo Ω, sono tra loro incompatibili. Se due eventi A e B sono incompatibili allora P(A ∪ B) = P(A) + P(B). In generale, la probabilità di n eventi E1, …, E_n a due a due incompatibili è data dalla somma delle loro probabilità:

Due eventi si dicono invece compatibili o congiunti se possono verificarsi contemporaneamente. Tali sono per esempio, nel lancio di un dado gli eventi A = {numero pari} e B = {numero maggiore di 4} che si verificano entrambi se il risultato del lancio è 6. Quando i due eventi sono compatibili si ha

Dato un evento E ⊆ Ω si dice evento complementare di E, e si indica generalmente con Ē, l’insieme complementare di E rispetto a Ω, definito anche dalla proposizione non E (indicata anche con ¬E). Si ha che:

Gli eventi certo e impossibile sono l’uno il complementare dell’altro. In generale, considerando n eventi E1, E2, …, E_n, a due a due incompatibili, la cui unione costituisce lo spazio campionario (e che dunque costituiscono una partizione di Ω), vale la proprietà

Tale famiglia prende il nome di sistema completo di alternative.