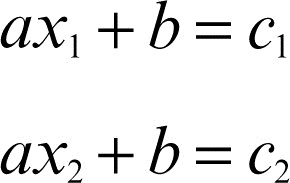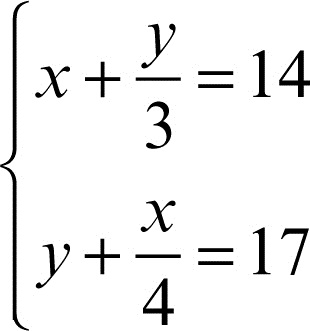falsa posizione, metodo di
falsa posizione, metodo di
falsa posizione, metodo di antico metodo iterativo per risolvere equazioni di primo grado in una incognita, sistemi di equazioni lineari e per la ricerca di soluzioni approssimate di equazioni di secondo grado. Il procedimento consiste nell’assegnare un valore arbitrario all’incognita (la falsa posizione) e nel costruire conseguentemente una proporzione da cui ricavare il valore vero dell’incognita.
La prima apparizione del metodo di falsa posizione si trova nel papiro di Ahmes, il cui nome deriva da quello dello scriba che lo trascrisse in ieratico attorno alla metà del 1600 a.C. riprendendolo verosimilmente da un papiro di circa due secoli più antico. Il papiro, detto anche «papiro Rhind», dal nome dell’antiquario scozzese Henry Rhind che lo acquistò in Egitto verso la metà del xix secolo e lo rese accessibile allo studio, è conservato quasi integralmente presso il British Museum di Londra e nei suoi tre metri di lunghezza contiene tabelle di frazioni e 84 problemi di geometria, di aritmetica e di quella che molti secoli dopo sarà denominata algebra. L’autore del papiro di Ahmes applica il metodo di falsa posizione per risolvere problemi formalizzabili con equazioni del tipo x + (1/n)x = b, con n e b interi positivi e x ∈ E, essendo E l’insieme numerico utilizzato dagli egizi, composto dai numeri interi positivi, dalla frazione 2/3 e da tutti i reciproci 1/n degli interi positivi n. Il problema concretamente proposto consiste nel trovare una quantità che aumentata della sua settima parte sia uguale a 19; la sua traduzione secondo le notazioni moderne è l’equazione in una incognita x:
L’autore del papiro adotta la semplice falsa posizione x = 7 e, sviluppando i calcoli a sinistra del segno di uguaglianza, trova il valore 8 anziché 19. Dividendo 19 per 8 e moltiplicandolo per 7, ossia stabilendo la proporzione x : 7 = 19 : 8, ottiene il risultato x = 133/8 = 16 + 1/2 + 1/8. La proporzione si basa implicitamente sulla congettura che il rapporto tra 19 e il valore trovato 8 è uguale al rapporto tra il valore vero di x e quello supposto. In sostanza, data una equazione del tipo ax = b, il metodo si basa sul supporre x = x1 ed effettuare il calcolo ax1 = b1. Ma allora dalla proporzione x : x1 = b : b1 si ricava x. Un metodo quale il precedente è detto di semplice falsa posizione poiché si è assegnato un solo valore particolare e, a partire da esso, si sono sviluppati i calcoli. Altri problemi richiedono invece una procedura che consiste nell’assegnare due valori particolari all’incognita (da qui il nome di doppia falsa posizione per tali metodi); si eseguono i calcoli per trovare gli errori commessi utilizzando tali valori, applicando alla fine una formula di interpolazione lineare. Si supponga, per esempio, di voler conoscere le lunghezze dei lati di un triangolo sapendo che il suo perimetro è uguale a 51 cm e che le lunghezze dei lati sono tre numeri consecutivi. Con il simbolismo moderno il problema si risolve semplicemente scrivendo l’equazione di primo grado x + (x + 1) + (x + 2) = 51, da cui si ricava x = 16. Con il metodo della doppia falsa posizione si può supporre che il primo lato sia lungo 10 cm, e allora il perimetro sarebbe 33 cm (prima falsa posizione), oppure sia di 11 cm, e allora il perimetro sarebbe 36 cm (seconda falsa posizione). Ciò implica che l’aumento di 1 cm nel lato causa un aumento di 3 cm nel perimetro. Rispetto alla prima falsa posizione si ricava che l’aumento del perimetro è 51 − 33 = 18 cm; usando la seconda falsa posizione si ricava che occorre aumentare proporzionalmente il lato della quantità 18 : 3 = 6 cm. La soluzione è appunto 10 + 6 = 16 cm. In generale, il metodo di semplice falsa posizione risolve equazioni del tipo ax = c, mentre la doppia falsa posizione risolve equazioni del tipo ax + b = c. In quest’ultimo caso, dalle due false posizioni si ha
Sottraendo membro a membro queste due equazioni si ottiene: a(x2 − x1) = (c2 − c1), che è del tipo aX = C e alla quale è quindi possibile applicare il metodo di semplice falsa posizione.
Il metodo si applica anche a problemi in più incognite e, quindi, a sistemi lineari. Il metodo di falsa posizione fu ripreso nel xiii secolo da L. Fibonacci nel suo Liber abaci, di cui si riporta qui un esempio: «Due uomini avevano dei denari. Il primo disse al secondo: se tu mi dessi la terza parte dei tuoi denari, ne avrei 14. E il secondo rispose: e se tu mi dessi la quarta parte dei tuoi, ne avrei 17».
Il problema consiste nel trovare quanti denari ha ciascuno e può essere modellizzato con un sistema di due equazioni lineari in due incognite:
Con il metodo della falsa posizione, si può porre, per esempio, x = 4; dalla prima equazione si ricava y = 30. Sostituendo questi valori di x e y nel primo membro della seconda equazione si ottiene il risultato 31, che ha un errore di 14 rispetto al valore dato 17. Se invece si pone x = 8, si ha y = 18; in questo caso il risultato ottenuto nella seconda equazione è 20, con un errore di 3 (rispetto a 17). La domanda usuale assume questa volta la forma: se con un incremento di 4 del valore di x si è diminuito l’errore di 11, di quanto si dovrà ancora aumentare il valore di x per diminuire ancora di 3 l’errore (e giungere così al valore 17)? Formulata conseguentemente la proporzione, la risposta è che si dovrà aumentare il valore di x di
Quindi, x = 8 + 1 + 1/11 = 9 + 1/11, da cui y = 14 + 8/11.