coniche, fascio di
coniche, fascio di
coniche, fascio di insieme di coniche analiticamente ottenuto dalla combinazione lineare delle equazioni di due coniche, dette coniche base, delle quali almeno una non sia degenere. Se le coniche base hanno equazioni ƒ(x, y) = 0 e g(x, y) = 0, l’equazione del fascio è λ ·ƒ(x, y) + μ · g(x, y) = 0, con λ, μ ∈ R, non entrambi nulli. Ogni conica del fascio si ottiene al variare dei parametri omogenei λ, μ o più semplicemente, con qualche limitazione, di un solo parametro non omogeneo dato dal loro rapporto. Sono detti punti base i punti, se ve ne sono, per i quali passano tutte le curve del fascio. Nel piano euclideo le coniche base possono essere circonferenze, ellissi, parabole e iperboli, conseguentemente si considerano i tipi di fasci di seguito elencati:
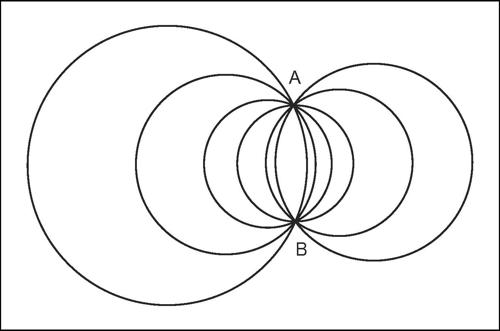
• fascio di circonferenze: è generato dalla combinazione lineare di due circonferenze. Può avere due, uno o nessun punto base a seconda della posizione reciproca delle circonferenze base;
• fascio di ellissi: è generato dalla combinazione lineare di due ellissi, purché siano verificate particolari condizioni. Infatti, mentre una qualsiasi combinazione lineare di due circonferenze genera una circonferenza, una combinazione lineare di due ellissi può generare sia un’ellisse sia un’iperbole. Per esempio, considerate le ellissi di equazioni x 2 + 2y 2 + −2 = 0 e 2x 2 + y 2 − 2 = 0, l’equazione (1 + 2k)x 2 + (2 + k)y 2 − 2(1 + k) = 0, ottenuta come loro combinazione lineare, rappresenta un’ellisse se e solo se i coefficienti (1 + 2k), (2 + k), (1 + k) sono di segno concorde, cosa che non accade, per esempio, ponendo k = −3/2, valore per il quale si ottiene l’equazione 2x 2 − y 2/2 − 1 = 0, che rappresenta un’iperbole. Un fascio di ellissi può avere da zero a quattro punti base, in relazione al numero minimo e massimo di intersezioni di due ellissi nel piano;
• fascio di parabole: combinando linearmente due parabole con asse parallelo a uno stesso asse coordinato, si ottiene ancora una parabola con la stessa proprietà. Per esempio da a1x 2 + b1x + c1 − y = 0 e a2x 2 + b2x + c2 – y = 0, si ottiene l’equazione
che rappresenta ancora una parabola dello stesso tipo. Può avere due, uno o nessun punto base a seconda della posizione reciproca delle parabole base;
• fascio di iperboli: è generato dalla combinazione lineare di due iperboli, purché siano verificate particolari condizioni, poiché la combinazione lineare di due iperboli può generare sia un’ellisse sia un’iperbole. Un fascio di iperboli può avere da zero a quattro punti base.
Nel piano proiettivo, dove non c’è distinzione tra circonferenze, parabole, ellissi e iperboli, una conica è rappresentata da un’equazione di secondo grado contenente sei parametri omogenei. Ne segue che un fascio di coniche è costituto da tutte le coniche che passano per quattro punti. Un fascio di coniche, nel piano proiettivo, costituisce una forma di prima specie.