Gibbs, fenomeno di
Gibbs, fenomeno di
Gibbs, fenomeno di in analisi, fenomeno che si riscontra nel caso di serie di → Fourier associate a funzioni che ammettono discontinuità di salto. In tal caso non solo la serie non può convergere uniformemente, ma si ha un errore supplementare, di segno opposto a quello del salto. Questo errore è in valore assoluto pari all’incirca a una percentuale fissa del 9% del salto, da entrambi i lati del punto di salto. Tale fenomeno scompare se al posto delle somme parziali si utilizzano le somme secondo Cesàro (integrale di → Fejér).
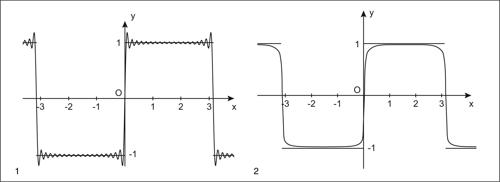
Le due figure riferite a questo lemma rappresentano rispettivamente la somma parziale per n = 19 (con 20 addendi non nulli)
della serie di Fourier di
e la corrispondente somma di Cesàro
Si noti che, se nell’eseguire la somma di Cesàro si tenessero in conto anche gli addendi nulli, si otterrebbe un risultato differente, anche se qualitativamente simile (si veda anche → sommazione, metodi di).