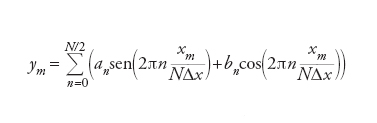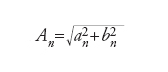FFT (Fast Fourier transform)
FFT (Fast Fourier transform)
Tecnica che consiste nel trovare i coefficienti per l’espressione di campioni in termini di una serie di Fourier di sinusoidi e cosinusoidi, di frequenze (temporali o spaziali, a seconda della natura del dominio) armoniche, troncata a Nyquist. Per segnali reali si tratta di risolvere il sistema lineare di N equazioni indipendenti in N incognite a{[ e b{[ per gli N campioni x{[=nΔx, dove Δx è il passo di campionamento:
con m=0,...,N. La sequenza
fornisce lo spettro numerico della sequenza x0,...,xn−1. La soluzione del sistema di equazioni richiede l’inversione di una matrice, che implica in generale un numero di operazioni proporzionale al quadrato del numero di equazioni (del numero di punti), il quale definisce a sua volta la risoluzione in frequenza 1/Δx della trasformata. Una complessità O(N2) rende rapidamente il calcolo proibitivo anche per risoluzioni relativamente basse. Da qui la necessità di algoritmi veloci (fast) che, sfruttando determinate proprietà della trasformata, riducano la complessità del calcolo. Tra questi, il più celebre è dovuto a James William Cooley e John Wilder Tukey (entrambi alla IBM) nel 1965, e del quale esistono diverse varianti, anche se in realtà si tratta di una indipendente riscoperta di un algoritmo già individuato nel 1805 da Carl Friedrich Gauss. Esso si basa sulla scomposizione ricorsiva della trasformata in due trasformate di dimensione dimezzata, fino alla dimensione due (trasformata di due punti). Questo approccio presuppone che la dimensione iniziale sia una potenza di due e conduce a una complessità O(N∙log2(N)), che cresce molto meno rapidamente del quadrato. Altri algoritmi FFT si basano sulla fattorizzazione di N in numeri primi (PFA) tra loro, o presuppongono N primo, o si basano su ancora altre fattorizzazioni. La FFT, di importanza capitale in molte applicazioni, è inoltre strettamente correlata con altre trasformate, quale la DCT (Discrete cosine transform). Questa è alla base di molte delle tecniche di compressione con perdita dei segnali audio (AAC, Vorbis, WMA, Mp3), delle immagini (jpeg) e dei video (MPEG, DV).
→ Musica elettronica ed elettronica musicale