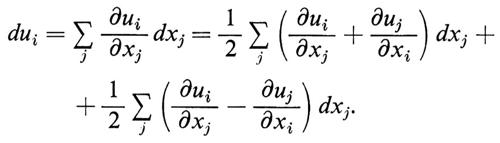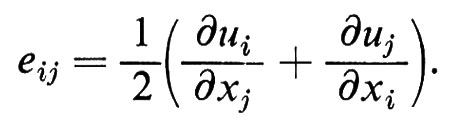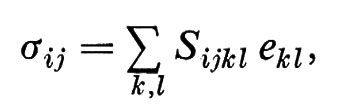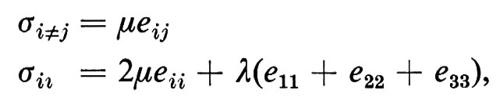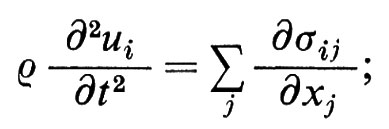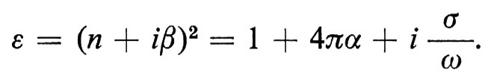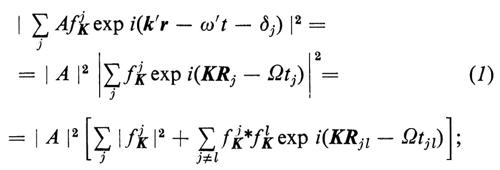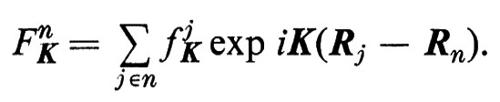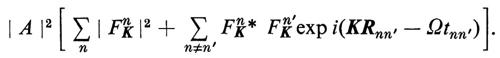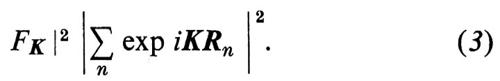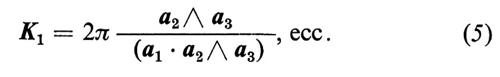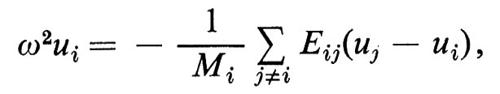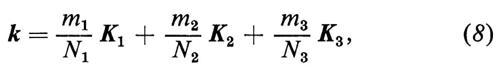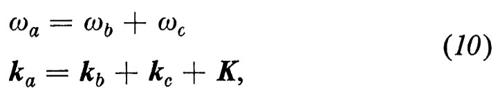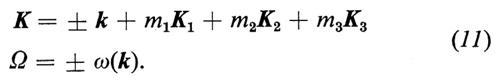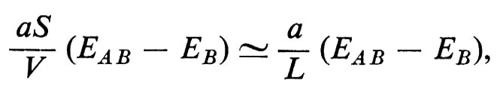Solidi, fisica dei

Solidi, fisica dei

di Jacques Friedel

SOMMARIO: 1. Introduzione. □ 2. Principali proprietà macroscopiche delle fasi condensate: a) struttura macroscopica; b) onde macroscopiche. □ 3. Struttura atomica: a) fasi amorfe e cristalli perfetti; b) cristalli reali. Agitazione termica. □ 4. Difetti statici in un cristallo reale. □ 5. La struttura elettronica: a) origine dell'ordine. Intensità fisico-chimica del legame; b) strutture a bande elettroniche nelle fasi condensate; c) critiche alle principali approssimazioni introdotte nello studio delle strutture elettroniche. □ 6. Struttura elettronica dei difetti. □ 7. Conclusione. □ Bibliografia.

1. Introduzione.

Gli stati condensati della materia, cioè i solidi e i liquidi, costituiscono, insieme ai gas e ai plasmi, il ‛mondo naturale' che l'esperienza su scala macroscopica della vita di ogni giorno ci presenta. Sin dai tempi più antichi gli uomini hanno imparato a riconoscere le principali caratteristiche dei solidi e dei liquidi e ne hanno fatto uso; in un certo senso la meccanica, la metallurgia, la cristallografia, l'ottica, l'elettricità, il magnetismo, la termodinamica si sono sviluppate come studi di aspetti distinti delle proprietà macroscopiche degli stati condensati della materia. Data però solo dai primi anni di questo secolo, con la scoperta dei raggi X, l'inizio dello studio su scala microscopica degli stati condensati della materia. Mediante esperimenti di diffusione di raggi X, von Laue, Bragg e altri confermarono l'ipotesi, precedentemente formulata da chimici e cristallografi - e in verità anche da Lucrezio -, secondo cui i liquidi e i solidi macroscopici sono tutti costituiti da un numero enorme di atomi. Essi mostrarono altresì come questi atomi siano in stretto contatto gli uni con gli altri e come quindi interagiscano fortemente. Queste interazioni portano a un ordine non casuale degli atomi: nei liquidi e nei solidi c'è per lo meno un certo grado di ordine su ‛brevi distanze' per ciò che riguarda il tipo dei legami atomici, la loro lunghezza e gli angoli che formano; in molti solidi questo ordine si estende su distanze macroscopiche e conduce a strutture cristalline, cioè a strutture ordinate su ‛lunghe distanze', triplicemente periodiche. Questa fu l'idea base che permise di fondare la fisica degli stati condensati della materia. Ben presto i lavori di Einstein e di Debye sull'agitazione termica nei cristalli e quelli di Fermi sugli elettroni in interazione posero le fondamenta della fisica dello stato solido, evidenziando la natura quantistica delle eccitazioni e le differenze tra le loro statistiche: la statistica di Bose-Einstein, per i quanti delle vibrazioni atomiche che possono coesistere in numero arbitrario, e quella di Fermi, per gli elettroni che non possono stare nello stesso stato con lo spin orientato nella medesima direzione. Da allora questo campo della fisica si è rapidamente sviluppato e si può affermare che, in seguito al lavoro di molti ricercatori, all'inizio dell'ultima guerra si è giunti a una buona conoscenza e a una chiara comprensione dei fenomeni fondamentali. Nacque allora il termine di ‛fisica dello stato solido', coniato da Seitz (v., 1940) per il suo libro, che rimane il testo basilare sull'argomento insieme con il precedente libro sui metalli di Mott e Jones (v., 1936) e i successivi lavori di Kittel (v., 1971⁴) e Ziman (v., 1960).

In questo campo di evidente complessità è utile e usuale distinguere tre livelli: le proprietà statiche e dinamiche su scala macroscopica; la struttura atomica, risultante dal tipo e dalla posizione dei nuclei tenuti insieme dai legami chimici; la struttura elettronica, che descrive sia questi legami coesivi sia le altre proprietà fisiche, ad esempio le risposte alle eccitazioni esterne di varia natura.

2. Principali proprietà macroscopiche delle fasi condensate.

a) Struttura macroscopica.

I liquidi e i solidi sono tutti caratterizzati dall'aver volumi molari simili. Questo significa che, da un punto di vista microscopico, si possono considerare gli elementi e i composti come densi ammassi di atomi o di ioni di dimensioni fisse, dell'ordine di pochi ångström. Queste dimensioni variano con regolarità lungo la tavola periodica, con uno o due minimi vicino al centro di ogni periodo e con un aumento regolare di periodo in periodo. I minimi della dimensione corrispondono a massimi della stabilità, che viene misurata dall'energia di coesione, cioè dall'energia richiesta per trasformare la fase condensata in un gas di atomi. Il valore tipico di questi massimi è di pochi eV per atomo, cioè di 50 ± 100 kcal/mole.

A seconda delle condizioni di temperatura e di pressione, una fase condensata di una data composizione chimica possiede almeno due possibili strutture in equilibrio termodinamico, separate da una transizione del primo ordine: una fase liquida (alta temperatura e bassa pressione), con caratteristiche isotrope e alta fluidità, capace cioè di cambiare forma molto rapidamente, e una o più fasi solide cristalline a temperatura più bassa e pressione più alta. Queste ultime sono caratterizzate da una grande viscosità, cioè dalla tendenza a mantenere inalterata la propria forma, e presentano anisotropie nelle proprietà fisiche, per lo meno sulla scala del singolo cristallo costitutivo. Va però notato che, a causa degli effetti quantistici che divengono rilevanti, l'⁴He non presenta fasi cristalline stabili a basse temperature. D'altra parte alcuni liquidi organici, durante il raffreddamento, mostrano fasi intermedie con scarsa viscosità ma con caratteristiche anisotrope: queste fasi di ‛cristallo liquido' o di ‛cristallo plastico' saranno discusse in seguito. Inoltre, dal momento che molte transizioni di fase, se non tutte, sono del primo ordine, appaiono fenomeni di isteresi allorquando le variazioni di pressione e di temperatura sono rapide. In particolare, è facile ottenere liquidi sovraffusi raffreddandoli repentinamente al di sotto del punto di fusione; questi solidi amorfi (isotropi) ottenuti con continuità dalla fase liquida non possono essere in equilibrio termico, tanto è vero che un raffreddamento più lento oppure un riscaldamento al di sotto del punto di fusione possono portare a una ricristallizzazione parziale o totale.

La stabilità (o metastabilità) delle fasi cristalline e amorfe può essere misurata a partire dalle proprietà elastiche, cioè attraverso le piccole deformazioni conseguenti all'applicazione di forze esterne. Nel caso di solidi isotropi, ad esempio una fase amorfa, si può definire, per un dato sistema di forze esterne, una pressione idrostatica p, che agisce perpendicolarmente a ogni superficie del solido, e uno sforzo di taglio s, che agisce tangenzialmente e in direzioni opposte su due facce opposte del solido. La pressione idrostatica produce una variazione δV del volume V senza modifica della forma, causa cioè una ‛dilatazione' (v. fig. lA), lo sforzo di taglio produce una variazione δϑ della forma senza variazione del volume (v. fig. 1 B): p, s, δV/ V e δϑ non dipendono ovviamente dalla forma esterna del solido. Se gli sforzi sono sufficientemente piccoli, le ‛distorsioni' δV/V o sono proporzionali ad essi:

p = K δV/V,

s = μ δϑ.

Questa è l'approssimazione che caratterizza l'elasticità lineare. Eventuali termini correttivi diventano rilevanti solo per grandi distorsioni, dell'ordine dell'unità: K è il modulo di rigidità, μ quello di scorrimento. Si usa definire anche la compressibilità χ = K^-1. Si possono definire altre coppie di costanti elastiche per i materiali isotropi: in una prova di trazione, ad esempio (v. fig. 1C), la relazione tra la forza traente applicata e l'elongazione δl/l è espressa dal modulo di Young E, mentre quella tra la contrazione trasversale e l'elongazione longitudinale è espressa dal rapporto di Poisson ν; E e ν sono collegati a K e a μ da semplici equazioni. Più in generale, in un mezzo anisotropo (cristallino), l'effetto degli sforzi può dipendere dalla loro orientazione. In condizioni di equilibrio gli sforzi applicati possono venir caratterizzati mediante le componenti perpendicolari e tangenziali delle forze agenti sulle facce di un cubo di materia avente una data orientazione, cioè mediante un tensore σ_ij in cui i si riferisce alla direzione della faccia e j a quella della componente della forza. In maniera analoga le distorsioni possono venir caratterizzate mediante la deformazione elastica u_i prodotta in ogni punto M della materia. Lo spostamento relativo di due punti vicini M(x_i) e M′(x_i + dx_i) è quindi:

Il secondo termine è semplicemente una rotazione; il primo termine descrive quindi la distorsione mediante un tensore e_ij i cui assi possono esser presi coincidenti con quelli del tensore degli sforzi:

È facile vedere che gli e_ii corrispondono alle elongazioni, la Σe_ii alla dilatazione δV/V e gli e_ij(j ≠ i) alle deformazioni di taglio δϑ. Nell'ambito di validità dell'approssimazione lineare dell'elasticità, la legge di Hooke dice che

dove il numero delle costanti elastiche Sijkl differenti è determinato dalla anisotropia del mezzo. Per mezzi isotropi si ha, per esempio,

dove λ e μ sono i ‛coefficienti di Lamé' (λ = K −μ/3).

Un solido può cambiar forma in maniera permanente se gli sforzi di taglio o di trazione diventano sufficientemente intensi da vincere la ‛resistenza solida' a bassa temperatura, oppure se sono applicati per un tempo sufficientemente lungo in contrasto con la ‛resistenza viscosa' ad alta temperatura. Nei materiali fragili, e specialmente a bassa temperatura, ciò può avvenire a causa del propagarsi di crepe e fratture; nei materiali plastici, invece, a bassa temperatura il cambiamento permanente di forma è dovuto allo scorrimento di alcune parti rispetto ad altre, mentre a temperature più elevate sono coinvolti anche fenomeni di trasporto di materia per diffusione. Nelle prove di trazione a bassa temperatura, generalmente, si misura il cambiamento dello sforzo applicato σ con l'elongazione e, mantenendo fissa la velocità di deformazione dε/dt; nelle prove di scorrimento si misura ε(t), mantenendo costante σ; in quelle di rilassamento invece si misura σ(t) per una deformazione ε costante.

b) Onde macroscopiche.

Nella materia allo stato condensato si possono propagare vari tipi di onde macroscopiche.

Onde elastiche. - Consistono di piccoli movimenti di una parte della materia rispetto alle altre. Se si applica a un cubetto di materia la legge fondamentale della meccanica, si ha (ρ è la massa specifica):

facendo poi uso della legge di Hooke, si ottiene un sistema di equazioni differenziali per lo spostamento u_i. In un corpo di dimensioni finite l'esatta forma delle onde dipende dalla forma del corpo: alcune onde, cosa ben nota ai sismologi, possono propagarsi lungo la superficie. In un solido isotropo, abbastanza esteso da potere trascurare le condizioni al contorno, si possono propagare, secondo ogni direzione, tre onde elastiche, una longitudinale e due trasversali di egual vettore d'onda ∣ k ∣ = 2π/λ. Per il corrispondente spostamento si può scrivere, nel caso di un'onda stazionaria, u(r, t) = A cos kr e^-iωt e, nel caso di un'onda progressiva, u(r, t) = A exp i(kr − ωt). Il fatto che sia cos x = (e^ix + e^-ix)/2 ed e^ix = cos x + i sen x autorizza a pensare che un'onda stazionaria risulti dalla sovrapposizione di due onde della stessa lunghezza d'onda che viaggino in direzione opposta, e che un'onda progressiva risulti dalla sovrapposizione di due onde stazionarie in quadratura. È facile vedere che la velocità di propagazione ω/k di queste onde, detta anche ‛velocità del suono', è data da (c/ρ)^1/2, dove c è una costante elastica che per le onde trasversali (o di taglio: A ⊥ k, c = μ) è Più piccola che per quelle longitudinali (o di compressione: A // k, c = λ + 2μ). Gli stessi risultati valgono sostanzialmente nel caso di cristalli anisotropi: ma, eccettuato il caso di direzioni con elevata simmetria, le tre onde elastiche di dato k hanno velocità differenti e caratteristiche miste. Nei liquidi isotropi le onde elastiche trasversali si smorzano rapidamente e solo quelle longitudinali riescono a propagarsi; questo è il motivo fondamentale che ci spinge a ipotizzare che alcune zone nell'interno della Terra siano allo stato liquido. Per i cristalli liquidi i risultati che si ottengono sono più complessi, a causa dell'anisotropia della struttura. Infine, nell'elio liquido, possono formarsi, per effetti quantistici, i ‛rotoni', cioè particolari onde con grandi vettori d'onda ma con frequenze basse.

Onde d'urto. - Sono onde di compressione di grande ampiezza che fanno aumentare repentinamente e in maniera considerevole la massa specifica e sia nei liquidi, sia nei solidi plastici in cui il limite elastico è molto al di sotto dell'aumento di pressione dovuto all'onda d'urto, è possibile trascurare tutti gli sforzi di taglio. Applicando le leggi di conservazione della quantità di moto e dell'energia durante il passaggio dell'onda d'urto, è possibile collegarne la velocità con l'aumento di pressione e con la variazione dell'energia di coesione in funzione del volume. Lo studio delle onde d'urto intense fornisce quindi indicazioni sulle forze interatomiche a brevissima distanza. Nel caso invece di onde d'urto deboli in un solido sorgono complicazioni dovute all'imperfetto smorzamento plastico degli sforzi di taglio durante la propagazione; le leggi che governano le deformazioni plastiche ad alta velocità non sono, infatti, ancora oggi ben conosciute.

Onde elettromagnetiche. - Sono quelle che forniscono le informazioni più dirette sulla struttura elettronica della materia. Da un punto di vista macroscopico possono venir esaminate facendo uso delle equazioni di Maxwell; la materia allo stato condensato risulta così caratterizzata da tre tipi di costanti.

1. I materiali che non possiedono permanentemente un momento magnetico (paramagnetici) o una polarizzazione elettrica (paraelettrici) possono venir caratterizzati dalla suscettività magnetica χ = M/H, dalla polarizzabilità elettrica α = P/E e dalla conducibilità elettrica σ = I/E, le quali collegano il momento magnetico indotto M, la polarizzazione indotta P e la corrente elettrica I al campo elettromagnetico (E, H). Queste grandezze variano con il vettore d'onda k e con la frequenza ω del campo elettromagnetico, ma, nel limite macroscopico infrarosso (ω e k → 0), si possono considerare costanti: in questa regione si può quindi distinguere tra conduttori (σ ≠ 0) e isolanti (σ = 0). A causa di questi effetti, le onde elettromagnetiche trasversali, dalla corrente alternata alle onde della luce, viaggiano nella materia allo stato condensato con velocità v differenti e si smorzano a una distanza 2π/k (profondità dell'effetto pelle) dalla superficie. Le costanti ottiche n = c/v e β sono legate ad α e σ e alla costante dielettrica complessa ε = ε₁ + iε₂ dalle eguaglianze

Esistono anche ‛onde di plasma' o onde elettromagnetiche longitudinali. A parte le onde di superficie di questo tipo, in campioni abbastanza grandi è possibile osservare onde di volume aventi una frequenza ω_p = (4πNe²/ε₁)^1/2: N_e è la densità dei portatori di carica elettronica ai quali è dovuta la conducibilità σ; la frequenza ω_p cade nell'ultravioletto per gran parte dei metalli e nell'infrarosso per i semiconduttori drogati.

2. Nei materiali ferroelettrici la polarizzazione permanente P provoca effetti di isteresi nel vettore spostamento elettrico D = E + 4πP. La medesima cosa avviene nei materiali ferromagnetici per il momento magnetico M e l'induzione B = H + 4πM. In questi casi, analogamente a quanto avviene nei materiali paraelettrici o paramagnetici quando viene applicato un forte campo elettromagnetico, la natura e il tipo di propagazione delle onde elettromagnetiche sono notevolmente più complicati, ma sono più ricchi di informazioni sulla struttura elettronica.

3. Struttura atomica.

a) Fasi amorfe e cristalli perfetti.

Se un fascio monocromatico di particelle incide su una porzione di materia allo stato condensato, il modo in cui esso viene diffuso è collegato alla struttura atomica (ed elettronica) della materia. Le particelle possono essere di diverso tipo: fotoni, atomi, elettroni, neutroni ecc. Questa proprietà è alla base di tutta una serie di tecniche che all'inizio comprendeva solo il metodo fondato sulla diffusione della luce e la cristallografia a raggi X e poi si è considerevolmente ampliata con l'introduzione della luce laser, della microscopia elettronica, dei reattori nucleari, della diffrazione di elettroni di bassa energia e di ioni. I recenti miglioramenti sia nelle sorgenti, sia nelle tecniche di rivelazione, hanno anche completamente rinnovato le tecniche classiche nell'ultravioletto e nei raggi X. Conviene quindi descrivere da questo punto di vista la struttura atomica della materia, quale oggi la conosciamo, ricorrendo anche a un certo formalismo matematico. Il fascio incidente può essere descritto come un'onda che si propaghi con ampiezza A exp i(kr − ωt). Il processo di diffusione spesso può venir trattato nell'approssimazione di Born, in cui ogni atomo j, indipendentemente, provoca una diffusione del fascio incidente in un fascio Af j_K exp i(k′r − ω′t − δ_j). f j_K è il ‛fattore di forma' dell'atomo relativo a un vettore di diffusione K = k′ − k, e lo sfasamento δ_j deve essere tale che i due fasci siano nella medesima relazione di fase durante la diffusione da parte dell'atomo j, in posizione R_j, al tempo t_j. L'intensità complessiva della parte diffusa diviene quindi

Ω = ω′ − ω e la variazione di frequenza durante la diffusione; inoltre si ha R_jl = R_l − R_j e t_jl = t_l − t_j; δ_j è stato scelto in modo tale che risulti (k′R_j − ω′t_j − δ_j) − (kR_j − ωt_j) = costante, per tutti i centri di diffusione j.

1. In una struttura atomica completamente casuale, come ad esempio in un gas monoatomico rarefatto, la media del secondo termine della (1) si annulla quando si esegue la somma su tutte le coppie di atomi j, l; l'intensità di diffusione è quindi direttamente legata a una media delle intensità di diffusione sui singoli atomi ∣ f j_K ∣²; essa varia con continuità con il vettore di diffusione e dipende dalla struttura degli atomi.

2. In una struttura con notevole ordine a corta distanza, come in un gas ad alta pressione, un liquido o un vetro, il secondo termine della (1) dà una correzione non nulla, la quale dipende direttamente dalla funzione di correlazione tra due punti S(R_jl, t_jl), che dà la probabilità di trovare un secondo atomo l a distanza R_jl da un primo atomo j, dopo un intervallo di tempo t_jl.

Nel caso di raggi X o di elettroni, Ω/ω generalmente è molto piccolo e si misura solamente la diffusione totale integrata su Ω, da cui si ricava la media temporale dell'ordine a breve distanza. In questo modo si vede che la maggior parte dei liquidi e delle fasi amorfe presenta strutture compatte: ogni atomo è circondato da un gran numero di atomi vicini, a distanze analoghe a quelle che si incontrano nei cristalli. Questo ordine è forte solo relativamente agli atomi piu vicini e, nei liquidi, diminuisce con l'aumentare della temperatura.

Nel caso di neutroni termici, d'altra parte, Ω/ω può diventare grande a causa del moto degli atomi; la luce laser ha una definizione in ω migliore di Ω. In entrambi i casi si può osservare la diffusione anelastica (Ω ≠ 0) che fornisce uno strumento per misurare la cinetica dell'ordine a breve distanza, rispettivamente su scala atomica o su una scala più macroscopica. Generalmente, per descrivere i moti macroscopici, si può far uso dell'idrodinamica classica e dell'equazione di diffusione con coefficienti di viscosità macroscopici. I moti su scala atomica sono molto più complicati e si comincia appena a comprenderli, nei liquidi elementari, facendo uso di procedimenti numerici su modelli; questi indicano una forte dipendenza dalla rigidità della repulsione interatomica a breve distanza.

L'⁴He è chiaramente un caso a parte. La sua superfluidità a bassa temperatura è dovuta a un fenomeno di condensazione causato dalla natura bosonica dei nuclei e dall'intensità delle interazioni internucleari, resa possibile dalla piccola dimensione dei raggi atomici e dalla leggerezza dei nuclei (v. criofisica). Le proprietà macroscopiche del trasporto e la quantizzazione delle linee di vortice possono venir descritte più o meno come verrà fatto in seguito per i superconduttori, ma la descrizione su scala atomica dello stato condensato è ancora ben lontana dall'essere completa. Lo stesso si può dire per l'³He liquido, i cui nuclei obbediscono alla statistica di Fermi, e per le soluzioni miste di ⁴He e ³He.

3. In un gas molecolare, in un liquido o in un vetro è utile separare in due parti la somma che compare nella (1), introducendo i fattori di diffusione molecolare

Trascurando i moti tra le molecole, la (1) diviene allora:

La diffusione su gas poliatomici rarefatti fornisce la struttura atomica delle molecole; per descrivere invece la diffusione su materia maggiormente condensata bisogna apportare le correzioni dovute all'ordine a breve distanza tra le molecole. I mutamenti dell'ordine a corto raggio sono più complicati da analizzare nei liquidi molecolari che in quelli monoatomici. Infine, negli aggregati di macromolecole, bisogna in generale tener conto dei moti intramolecolari; infatti, la viscosità dei polimeri a catena lunga dipende dalla rottura della catena molecolare indotta termicamente.

4. In un cristallo perfetto gli atomi sono posti in una struttura periodica su tre dimensioni, cosicché ogni dettaglio della configurazione viene riprodotto da una traslazione T_A di un periodo A del reticolo di Bravais che caratterizza la periodicità del cristallo:

A = n₁a₁ + n₂a₂ + n₈a₃. (2)

Gli n_i sono numeri interi e gli a_i sono tre ‛periodi elementari' e non complanari che formano la ‛cella unitaria' del cristallo (v. fig. 2A) La ‛base' dal cristallo, cioè gli atomi contenuti in una cella con origine R_n, può esser pensata come una molecola e l'intero cristallo come una struttura ordinata di queste molecole, tutte aventi lo stesso fattore di diffusione Fn_K = F_K. L'intensità totale di diffusione diviene dunque:

Di solito queste molecole sono così fortemente legate tra loro da perdere ogni individualità fisica; pur tuttavia l'analisi geometrica con cui si è ottenuta la (3) rimane valida.

Nel fattore di struttura ∣ Σ_n exp iKR_n ∣², la media sugli n periodi del cristallo dà, per la maggior parte dei valori di K, un valore che è al massimo dell'ordine dell'unità: il cristallo diffonde quindi all'incirca come uno dei suoi periodi. Tuttavia, quando K ha un valore vicino a quello per cui KR_n è un multiplo intero di 2π per tutti i valori di n, allora i termini di interferenza nella (3) si sommano. Questa condizione è evidentemente soddisfatta se K è un periodo del ‛reticolo reciproco'

K = m₁K₁ + m₂K₂ + m₃K₃, (4)

con m_i interi e

Quindi un fascio di raggi X di data lunghezza d'onda viene riflesso selettivamente a un certo angolo da ogni piano del reticolo di Bravais: per esempio K₁ perpendicolare a (a₂, a₃). Secondo queste formule, l'intensità totale diffusa dovrebbe essere N² volte maggiore di quella di una singola cella, se ci sono N celle nel cristallo, e dovrebbe diminuire quando K si allontana dalla ‛condizione di Bragg' (4) per più di 2π/L, dove L è la dimensione del cristallo. La diffusione dei raggi X è quindi particolarmente selettiva. Questa è la base di tutti i metodi per determinare la struttura dei cristalli.

I cristallografi hanno esaminato sistematicamente un numero enorme di fasi cristalline e le hanno classificate riunendole in sette tipi di reticoli cristallini, a seconda delle simmetrie del reticolo di Bravais, e in 32 classi di gruppi di trasformazioni di punti a seconda della massima simmetria della base. Per mostrare meglio queste simmetrie, la cella unitaria non viene definita come un parallelepipedo (a₁, a₂ , a₃), ma come una ‛cella equivalente di Wigner-Seitz': essa è il minimo volume contenuto all'interno dei piani mediani di ciascun periodo A del reticolo di Bravais; l'origine dalla quale tutti questi periodi vengono presi è un punto di massima simmetria per il cristallo (v. fig. 2B). Combinando insieme questi due tipi di simmetrie si ottengono 7 × 32 + 6 = 230 gruppi spaziali; i sei gruppi supplementari comprendono simmetrie miste caratteristiche dei cristalli: invarianza per spostamenti elicoidali, cioè traslazioni accoppiate a rotazioni.

Le alte intensità di diffusione ottenute hanno spinto a far cristallizzare anche molecole grosse, come quelle biologiche, per poterne studiare la struttura atomica. Oltre alle correzioni dovute a effetti secondari, quali l'assorbimento e la diffusione Compton, nell'analisi dell'intensità di diffusione da quantitativi macroscopici di materia sorgono difficoltà a causa degli effetti di diffusione multipla. In un policristallo, cioè in un aggregato di cristalli con varie orientazioni, un fascio diffuso da un cristallo può trovarsi in condizioni adatte per essere diffratto da un altro. In un cristallo singolo, ma sufficientemente grande, il fascio di raggi X diffuso da un piano di Bravais del cristallo viene parzialmente ridiffuso indietro da un piano parallelo e così via. Il fascio diffuso non può più venir trattato come una piccola correzione del fascio incidente, come invece è implicito nella teoria cinematica delle equazioni (1), (3). La teoria dinamica pone sullo stesso piano questi due (o più) fasci e considera appunto due onde che si propagano nel cristallo lungo i piani di diffusione exp ikr ± exp ik′r ∝ exp 1/2 i(k + k′)r × (cos Kr/2 o sen Kr/2); entrambe oscillano lungo K con una lunghezza d'onda eguale alla distanza tra due piani di diffusione. Questa analisi indica come la larghezza della condizione di diffrazione (4) non scenda mai al di sotto di un valore Δ piccolo ma finito e, corrispondentemente, come l'intensità diffratta da un cristallo perfetto non possa mai superare quella diffratta da un cristallo di dimensione 2π/Δ. Infine, se la diffusione avviene per trasmissione lungo il cristallo, una delle due onde dinamiche è assorbita meno dell'altra, dato che l'ampiezza delle sue oscillazioni lungo K diminuisce nelle regioni di minor densità elettronica; in condizioni favorevoli, tutti i nuclei degli atomi nel cristallo si trovano nei nodi, di modo che l'onda viene assorbita molto poco e può attraversare cristalli anche notevolmente spessi (‛effetto Borrmann').

b) Cristalli reali. Agitazione termica.

In un cristallo reale non si osserva mai la perfetta, triplice periodicità che si è ipotizzata nel caso di un cristallo perfetto. In primo luogo gli atomi si muovono di continuo intorno alla loro posizione di equilibrio, a causa di eccitazioni esterne (onde elastiche), a causa della temperatura non nulla (agitazione termica) o semplicemente a causa della relazione di indeterminazione (vibrazioni di punto di zero). Queste posizioni di equilibrio non si trovano poi mai ordinate in un reticolo perfettamente periodico, la loro disposizione può presentare imperfezioni che si possono considerare statiche rispetto alle frequenze caratteristiche dell'agitazione termica (≃ 10¹³ s^-1), anche se in parte mutano col tempo. Prenderemo dapprima in considerazione solamente l'agitazione termica di un cristallo altrimenti perfetto.

Il moto degli atomi intorno alle loro posizioni medie introduce un disordine che generalmente viene analizzato in termini di ‛onde elastiche'. Queste possono venir considerate come indipendenti nel limite in cui siano piccoli gli spostamenti atomici u_j, cioè per temperature non troppo elevate. In questo limite, ogni atomo oscilla sotto l'influenza dei vicini, sottoposto a forze proporzionali allo spostamento relativo. La meccanica elementare fornisce la soluzione di un sistema di equazioni dinamiche che collegano linearmente l'accelerazione del singolo atomo d²u_j/dt² allo spostamento rispetto ai vicini u_l − u_j. Le onde progressive {u_j} ∝ exp iωt soddisfano un sistema di equazioni lineari che formalmente si può scrivere nella forma

D{u_j} = ω²{u_j}, (6)

dove ω è la frequenza, {u_j} è la matrice a una colonna degli spostamenti degli atomi e D è un opportuno ‛operatore dinamico' lineare. Nel caso di una catena lineare di atomi, ad esempio, un'onda longitudinale è descritta dall'espressione seguente:

dove le E_ij sono costanti relative alle forze elastiche tra gli atomi i e j. D quindi è una matrice tale che D_i±j = − E_ij/M_i e D_ii = (Σ_j±iE_ij)/M_i.

Generalmente D dipende dalla struttura del cristallo e ovviamente commuta con l'operatore di traslazione T_A definito dal reticolo di Bravais (2). Per un ben noto teorema, si può allora scegliere come {u_j} un autovettore di T_A; con una scelta opportuna di un vettore costante k, l'autovalore di T_A può essere scritto nella forma exp ikA:

T_A{u_j} = exp ikA{u_j}.

Dal momento che T_A non è un operatore hermitiano, a priori k può essere complesso. Se allora si scrive {u_j} nella forma

{u_j}= {uj⁰ exp ikA_n}, (7)

dove A_n è il periodo n-esimo cui appartiene l'atomo j, la condizione precedente richiede che uj⁰ abbia la periodicità del reticolo, cioè che assuma gli stessi valori su atomi j equivalenti appartenenti a celle unitarie differenti. Si può supporre che le onde di Bloch (7), quando si propagano in cristalli infiniti, soddisfino la condizione periodica di Bloch-von Karman u_j+Ni ≡ u_j, dove l'atomo j + N_i differisce dall'atomo j per una grande traslazione N_ia_i(i = 1, 2, 3). Allora il k che compare nella (7) deve essere reale e soddisfare la relazione

dove i K_i sono i periodi del reticolo reciproco (5). Se N_i tende all'infinito, i valori quantizzati di K finiscono per variare quasi con continuità nello spazio reciproco, mantenendo però costante la densità.

Tutte le funzioni periodiche nello spazio reale possono essere analizzate in serie di Fourier con vettori d'onda eguali ai periodi del corrispondente reticolo reciproco. Ogni onda di Bloch (7) può quindi essere riscritta come una nuova onda di Bloch con un k che differisce da quello vecchio per un periodo nello spazio reciproco. Nello ‛schema a zona ridotta' si considerano solo quelle onde i cui vettori d'onda cadono in una singola cella unitaria del reticolo reciproco; esse sono le uniche fisicamente distinte. Una maniera conveniente di prendere questa cella unitaria consiste nello scegliere il minimo volume contenuto all'interno di tutti i piani bisecanti i periodi del reticolo reciproco. Questa è la ‛prima zona di Brillouin', che ha la proprietà di simmetria delle onde ω(k) ≡ ω(− k), come si dimostra cambiando il segno del tempo nell'equazione dinamica (6); essa è l'equivalente nello spazio reciproco dei vettori k della cella di Wigner-Seitz precedentemente definita nello spazio reale dei vettori r. Per ogni k esistono diverse soluzioni in ω(k), che variano con continuità nello spazio reciproco. Ognuno di questi rami ha N₁N₂N₃ soluzioni in k, pari cioè al numero di celle unitarie del cristallo. Il numero dei rami ω(k) deve essere quindi eguale al numero di gradi di libertà per cella unitaria, cioè eguale a tre volte il numero q di atomi per cella. Tre di questi rami vanno a zero per k = 0: sono i rami acustici, in cui il moto relativo degli atomi si annulla quando la lunghezza d'onda tende all'infinito; la loro pendenza iniziale (dω/dk) = (ω/k)₀ dà la velocità delle onde acustiche macroscopiche (trasversali, longitudinali e miste) nel cristallo (v. fig. 3). Se c'è più di un atomo per cella nel cristallo, gli altri rami hanno frequenza finita ω₀ per k = 0 e corrispondono a moti relativi degli atomi che non si annullano al crescere verso l'infinito della lunghezza d'onda. Se gli atomi sono carichi (ioni) e per opportune simmetrie, queste onde producono una polarizzazione locale che può interagire con le onde luminose e portare a un assorbimento ottico: da qui il loro nome di rami ‛ottici'. A causa di questo accoppiamento, i rami orizzontali di fononi ottici trasversali si mescolano fortemente con il ramo quasi verticale di fotoni ω = kc/n (c/n è la velocità della luce nel solido) nella regione in cui si intersecano (v. fig. 4). Le eccitazioni che si propagano nel cristallo hanno quindi un carattere misto tra elastico ed elettromagnetico. Per k minore del valore di intersezione, la luce si propaga a una velocità inferiore con un indice di rifrazione n determinato dalla polarizzazione statica, alla quale contribuisce il termine dovuto allo spostamento degli ioni nel campo elettrico; per k più grandi del valore di intersezione la velocità della luce dipende solo dalla polarizzazione elettronica degli ioni.

La natura discontinua della struttura atomica del cristallo determina un taglio nelle frequenze delle onde elastiche. Se ne può stimare approssimativamente la posizione facendo uso del ‛modello di Einstein', in cui ogni atomo oscilla con frequenza ω_E nella gabbia formata dagli atomi vicini che si suppone siano a riposo; un'altra stima, ω_D, dovuta a Debye, assume invece che le N_q onde elastiche abbiano tutte la stessa velocità, eguale a quella delle onde sonore. Entrambe le valutazioni portano al medesimo ordine di grandezza ω_E ≃ ω_D ≃ √-2-C-/-ρ = 10¹³ s^-1, dove C è una costante elastica e ρ è la massa specifica.

In questa analisi, in cui si fa uso della meccanica classica, l'ampiezza delle onde elastiche è piccola, ma arbitraria. In effetti, l'equazione (6) è l'estensione a più corpi della teoria dell'oscillatore lineare. L'equazione di Schrödinger corretta che sostituisce la (6) porta alla quantizzazione delle ampiezze, e quindi dell'energia E, nella forma, usuale in questi casi,

E = (n + 1/2)ℏω, (9)

in cui n è un intero. Un quanto di vibrazione (δn = 1) con energia ℏω si chiama ‛fonone'. Anche nello stato più basso (quando è n = 0, cioè non c'è nessun fonone) ogni onda elastica ha un'energia non nulla, che si associa al contributo da essa apportato al moto di ‛punto zero'. L'ampiezza della vibrazione di una data onda ω(k), e quindi la sua energia media, aumenta ovviamente con la temperatura. Il contributo dell'agitazione termica al calore specifico C_v risente, come è naturale, alle basse temperature, della quantizzazione (9) e dipende dalla velocità del suono; è facile mostrare che, per T ≪ T_D, è C_v = AT³, dove A dipende dalle costanti elastiche. A temperature più elevate (T ≫ T_D) il calore specifico, evidentemente, raggiunge un valore di saturazione pari a k_B per ogni grado di libertà del cristallo, e quindi segue la legge di Dulong e Petit. La temperatura limite di Debye è quella per cui T_D = ℏω_D/k_B ≃ 100 °K. In effetti, con l'aumentare della temperatura, molti solidi passano attraverso una successione di fasi cristalline di equilibrio, ciascuna delle quali ha un'energia interna più piccola, ma una entropia maggiore, della precedente. Ad esempio, si può mettere in rapporto la struttura cubica a corpo centrato, che si osserva in molti metalli a temperature elevate, con la costante di taglio, il cui valore, in questa struttura, è singolarmente piccolo.

È chiaro, proprio per come sono stati definiti, che i fononi sono dei bosoni: seguono cioè la statistica di Bose-Einstein, per cui in ogni onda elastica ω(k) ne può essere creato un numero arbitrario. Tuttavia, quando il numero dei fononi diventa grande, cioè quando l'ampiezza dell'onda diviene grande, un'analisi più accurata deve tener conto dei termini non armonici dovuti al fatto che le forze interatomiche non sono più proporzionali agli spostamenti, quando questi diventano ampi. Si possono misurare questi effetti anarmonici quando sono provocati da sforzi uniformi e intensi (forti pressioni idrostatiche, incurvamento di piccoli cristalli perfetti, onde d'urto), ma per piccole lunghezze d'onda o nei rami ottici essi sono ancora oggi conosciuti molto male. Come è naturale, essi corrispondono quasi generalmente a una diminuzione del valore delle costanti elastiche effettive sotto l'effetto di una dilatazione e a un aumento sotto l'effetto di una compressione. Si può dar conto dell'espansione del reticolo che ne segue e della diminuzione delle costanti elastiche all'aumentare dell'ampiezza dell'onda e quindi della temperatura, per lo meno in un modello termodinamico approssimato che trascuri la vita media finita dei fononi (modello di Mie-Gruneisen). In realtà, le deviazioni anarmoniche portano a un accoppiamento tra i fononi che ne limita la vita media con reazioni del tipo k_a → k_b + k_c, k_a + k_b → k_c, k_a + k_b → k_c + k_d ecc. A queste reazioni, fintantoché sono rare, cioè per temperature non troppo elevate, si possono applicare le leggi di conservazione. La prima reazione, quindi, con ovvia notazione, dà

in cui K è un periodo del reticolo reciproco (4), che compare a causa della indeterminazione nei k delle onde di Bloch.

Questi urti fonone-fonone limitano la conducibilità termica degli isolanti a temperature elevate. Con argomentazioni un po' alla buona si può mostrare che la conducibilità termica deve variare come T^-1 se in questa regione continuano a prevalere le reazioni a tre fononi. A temperature più basse, per T ≪ T_D, solo le reazioni (10) con K ≠ 0 nello schema a zona ridotta contribuiscono alla resistività termica, dal momento che esse sono le uniche che possono alterare il momento medio delle onde acustiche: sono i cosiddetti processi umk lapp; la probabilità di queste reazioni tuttavia tende a zero al diminuire di T e, in tale caso, la conducibilità termica risulta invece limitata dalla diffusione dei fononi da parte di difetti statici del reticolo. Ogni tipo di difetto diffonde di preferenza i fononi che hanno lunghezze d'onda con esso comparabili; così le impurità e le dislocazioni, come verrà precisato in seguito, predominano nei processi di diffusione a temperature più elevate di quelle alle quali sono invece più importanti i bordi dei grani o le superfici del cristallo. A queste basse temperature i fononi si comportano come portatori liberi con un cammino libero medio pari a λ; applicando quindi le equazioni classiche dei gas perfetti, la conducibilità termica diviene C_vλ/3, dove C_v è il calore specifico del reticolo. Per T → 0, si ha C_v ∝ T³, secondo la legge di Debye, e λ = cost. La conducibilità termica risulta quindi proporzionale a T³ attraverso una costante proporzionale alle dimensioni del cristallo ('legge di Casimir').

Si può studiare l'agitazione termica degli atomi nei cristalli con esperimenti di diffusione dinamica di neutroni o di luce e, in misura minore, mediante diffusione integrata di raggi X o di elettroni. Questo movimento, che rompe parzialmente la periodicità del cristallo, abbassa l'intensità dei picchi di diffrazione elastica (3), dal momento che questa misura la probabilità che ha il cristallo di trovarsi nello stato più stabile, e introduce una distribuzione di diffrazione anelastica continua (con un'alterazione della frequenza dell'ordine della frequenza di oscillazione degli atomi nei solidi, cioè ≃ 10¹³ s^-1) nello spazio reciproco.

Per temperature non troppo elevate, fintanto che si possono analizzare i movimenti degli atomi mediante onde elastiche indipendenti ω(k), applicando le leggi generali di conservazione al processo di diffusione, si ha:

In queste equazioni, che rimpiazzano la condizione (4) per la diffusione elastica da parte di un cristallo perfetto, il segno (+ o −) dipende dal diminuire o dall'aumentare dell'ampiezza dell'onda elastica durante il processo di diffusione, dal fatto cioè che vi sia assorbimento o emissione di un fonone. A causa delle imperfezioni del reticolo e dell'accoppiamento tra le onde elastiche, queste condizioni non sono assolute. In effetti le curve di dispersione ω(k) delle onde elastiche sono ora note con molta accuratezza per numerosi cristalli di semplice struttura, ma la larghezza in ω e le sue variazioni con la temperatura sono conosciute ancora molto male, in parte a causa della scadente definizione in energia dei neutroni a disposizione in tutti i reattori, tranne in quelli a flusso elevato.

La larghezza in ω delle onde elastiche aumenta con la temperatura, ma perfino al punto di fusione, in generale, è una frazione sufficientemente piccola di ω perché le onde elastiche mantengano la loro individualità fisica. Per alcune onde elastiche si verificano notevoli aumenti della larghezza nell'intorno di un passaggio tra due fasi solide che avvenga in maniera continua, senza calore latente (nelle transizioni del ‛secondo ordine'), o quasi continua, con poco calore latente (in alcune transizioni del ‛primo ordine'): ad esempio, nelle transizioni delle leghe tra una fase di ordine e una di disordine o nei passaggi da una fase ferroelettrica a una paraelettrica, ecc. Si osservano allora, vicino ai punti di transizione, forti fluttuazioni del parametro di ordine che descrive la transizione, le quali corrispondono a grandi ampiezze delle corrispondenti onde elastiche cui fanno seguito forti accoppiamenti anelastici. Se, come nel caso delle transizioni ferro-paraelettriche, intervengono onde ottiche di grande lunghezza d'onda, la larghezza in ω diviene più grande della frequenza media, che tende a zero con k; probabilmente quindi anche il concetto stesso di onde elastiche indipendenti perde di significato.

Sorgono complicazioni anche nel corso e in prossimità di quelle fasi intermedie che si possono osservare tra le fasi di cristallo e di liquido in alcuni cristalli, per lo più molecolari. Per esempio: a) cristalli con molecole quasi sferiche, come l'UF₆ o il benzene, presentano transizioni verso una fase ‛plastica' in cui i baricentri delle molecole si ordinano secondo una struttura, mentre l'orientazione delle molecole perde il suo ordine su lunga distanza. Questo fenomeno porta a una figura di diffrazione a raggi X maggiormente simmetrica, ma con un fondo di diffrazione continuo nello spazio reciproco. Questo effetto è molto simile alle trasformazioni da una fase di ordine a una di disordine che si osservano nelle leghe; b) cristalli con molecole allungate presentano una o più transizioni a fasi ‛mesomorfiche' nelle quali viene mantenuta l'orientazione delle molecole, mentre i baricentri perdono l'ordinamento su distanze lunghe; di solito queste fasi presentano caratteristiche di fluidità proprie di un liquido. Nelle fasi ‛nematica' e ‛smettica', le molecole sono tutte disposte parallelamente, ma la posizione dei baricentri, rispettivamente nell'intero volume o sui piani paralleli, è casuale; nelle fasi ‛colesteriche' i baricentri si trovano in posizioni casuali e l'orientazione varia nello spazio come i raggi di una curva elicoidale. Queste fasi, cui si dà anche il nome di cristalli liquidi, presentano ovviamente particolari figure di diffrazione; infatti, il passo dell'elica nelle fasi colesteriche, o la lunghezza propria delle perturbazioni introdotte, per esempio, da correnti elettriche in una fase nematica, permette un forte accoppiamento con le onde luminose. Queste fasi sono poco stabili, usando come criterio di misura il calore necessario per cambiare fase; sono perciò molto sensibili anche a piccole perturbazioni esterne (temperatura, campi elettrici o magnetici). Attualmente esse vengono quindi studiate in previsione di una loro possibile applicazione ottica nel campo dell'informazione, ma, a causa della loro notevole viscosità, non possono essere usate in apparecchiature veloci. È opportuno inoltre osservare che un certo numero di materiali biologici, dalle cellule della pelle alle molecole delle membrane e alle molecole di DNA dei cromosomi, presentano ordinamenti molto simili a quelli delle fasi mesomorfiche.

Un caso a parte, infine, è costituito dall'³He solido, in cui le intense vibrazioni degli atomi fanno sì che forti interazioni di scambio tra i nuclei giochino un ruolo significativo nella coesione.

4. Difetti statici in un cristallo reale.

In un cristallo sono sempre presenti dei difetti; questo, in parte, è dovuto al fatto che i cristalli, rispetto ai liquidi e ai gas, hanno una forte viscosità e quindi solo di rado sono completamente in equilibrio termodinamico. I difetti hanno anche un ruolo essenziale in molte delle proprietà fisiche del cristallo: il loro studio sistematico ha rappresentato uno degli aspetti caratteristici della fisica dello stato solido negli ultimi venti anni.

A seconda delle loro dimensioni, i difetti possono essere classificati in difetti puntiformi, dislocazioni e superfici. Le superfici, limitando le dimensioni del cristallo, allargano le righe degli spettri X. Le irregolarità puntiformi e lineari producono un fondo elastico continuo; in effetti, in circostanze favorevoli si possono osservare localmente diverse condizioni di diffusione prodotte da questi difetti mediante la riflessione di fasci paralleli da parte del cristallo (tecnica a raggi X di Berg-Barret) o la trasmissione attraverso un singolo cristallo sottile (microscopia elettronica; tecnica a raggi X di Lang). Si può così studiare la geometria dei difetti nel volume del cristallo mediante l'effetto dinamico di Borrmann di cui si è parlato precedentemente. D'altra parte si è fatto anche uso della diffusione anelastica di neutroni o di luce per studiare le modificazioni dell'agitazione termica dovute a imperfezioni: eventuali onde elastiche locali, o cambiamenti nella densità degli stati o nell'ampiezza locale delle onde elastiche nel cristallo.

Difetti puntiformi. - I materiali cristallini non sono mai perfettamente puri o stechiometrici: hanno sempre delle imperfezioni che, se sufficientemente rare, si trovano disperse su scala atomica in modo da render massima la loro grande entropia di configurazione. Questi ‛difetti puntiformi estrinseci' possono per la maggior parte essere misurati e in certi casi il loro numero può essere ridotto, con adatti trattamenti termici e chimici, fino a valori corrispondenti a concentrazioni atomiche inferiori a 10^-6. In casi speciali, come ad esempio nei semiconduttori elementari, la concentrazione atomica delle impurità elettricamente attive può scendere anche a valori dell'ordine di 10^-10. All'estremo opposto, molti elementi si mescolano a livello atomico in concentrazioni molto elevate dando luogo a ‛soluzioni solide'; in generale, la loro distribuzione è essenzialmente casuale per l'azione dell'entropia di configurazione. Ma anche se perfettamente puro e stechiometrico, un cristallo può presentare un numero apprezzabile di difetti puntiformi intrinseci introdotti con trattamenti opportuni: trattamenti termici, irraggiamento, deformazioni plastiche.

Si è quindi portati a definire i difetti puntiformi indicati nel seguito. Le impurità dovute ad atomi ‛sostitutivi' prendono il posto di altri atomi del cristallo perfetto (fig. 5A). A causa delle loro dimensioni atomiche differenti, in generale questi atomi sostitutivi producono distorsioni nel cristallo e quindi non se ne può dissolvere una grande quantità né si può giungere a grandi soluzioni solide in equilibrio termodinamico se le dimensioni differiscono per molto più del 15%. In generale, queste distorsioni presentano la simmetria imposta dal reticolo che le circonda, a parte casi particolari in cui si incontra una simmetria inferiore: per esempio, quando si hanno molecole sostituenti (ad esempio OH^- oppure O2^- al posto di Cl^- nei cloruri alcalini); ioni sostitutivi di piccole dimensioni, come ad esempio Li⁺ al posto di K⁺ in KCl; impurità con il guscio parzialmente riempito, che presentano una degenerazione orbitale aumentata da una distorsione del reticolo (‛effetto Jahn-Teller').

Le ‛lacune' si possono considerare alla stregua di uno speciale tipo di impurità di sostituzione. Nei cristalli elementari si tratta di atomi mancanti, nei solidi ionici di ioni mancanti e nei cristalli molecolari di molecole mancanti (fig. 5B, C, D, E). Ovviamente l'energia di formazione U delle lacune è proporzionale all'energia di coesione, sicché la loro concentrazione all'equilibrio termodinamico, dell'ordine di exp (− U/k_BT), raggiunge valori dell'ordine di 10^-4 ÷ 10^-3 al punto di fusione.

Queste concentrazioni piccole, ma non nulle, sono responsabili di quasi tutti i fenomeni di diffusione ad alta temperatura nei cristalli: autodiffusione e diffusione delle impurità, cambiamenti di fase per formazione di centri e loro successivo accrescimento, reazioni chimiche, elettrolisi, scorrimenti, processi di sinterizzazione. Sfruttando l'agitazione termica, un atomo adiacente, come ad esempio l'atomo a della fig. 5B, può saltare nella lacuna posta in b trasferendola così da b ad a. In questo modo, a un flusso di lacune da destra verso sinistra corrisponde un flusso di materia da sinistra a destra; questo processo viene attivato termicamente con un'energia di attivazione che è data dalla somma delle energie di formazione e di spostamento della lacuna. In generale le due forme di energia sono del medesimo ordine di grandezza e quindi la somma risulta proporzionale all'energia di coesione per atomo e del suo stesso ordine di grandezza. Nei solidi ionici entrambi i tipi di lacune (positive e negative) devono spostarsi per produrre un trasporto globale di materia con conseguente cambiamento di forma, come nel caso di uno scorrimento o di una sinterizzazione; nell'elettrolisi e in molte reazioni chimiche basta che si muova un solo tipo di lacuna; nei composti è il difetto meno mobile quello che limita la velocità di trasporto della materia, quello più mobile invece limita la velocità di reazione. Se si raffredda rapidamente un campione a partire da temperature elevate, si possono mantenere le lacune anche a temperature basse in condizioni di sovrassaturazione; a temperature medie, esse possono ancora diffondere, fermarsi su linee o superfici di dislocazione e quivi scomparire; se la sovrassaturazione è sufficientemente intensa possono anche formare agglomerati. In questo modo le lacune doppie, che spesso si formano temprando un metallo e che sono più mobili delle lacune singole, rendono più complessa l'analisi del riassestamento dopo il raffreddamento. Gli ammassi più grandi sono meno mobili; quando non sono composti solo da poche lacune, generalmente producono piccoli anelli di dislocazioni le cui dimensioni, come vedremo in seguito, aumentano progressivamente; si possono anche formare piccole bolle, specie se rese maggiormente stabili dalla presenza di impurità gassose che si concentrano al loro interno. In una lega, le lacune da raffreddamento possono anche venire catturate dagli atomi disciolti, che diventano quindi maggiormente mobili a temperature medie: è questa la maniera in cui si formano aggregati di atomi di Cu a bassa temperatura nelle zone di Guinier-Preston dei durallumini AlCu.

Gli atomi di ‛impurità interstiziali' sono quelli che occupano gli interstizi di un reticolo perfetto (v. fig. 6A); solo atomi piccoli (ad esempio H, He, B, C, N ecc.) o atomi o ioni molto polarizzabili (come Cu, Ag, Au) possono dissolversi con questo meccanismo in quantità apprezzabili senza avere energie di distorsione eccessivamente elevate.

Quindi gli atomi ‛autointerstiziali', cioè gli atomi dello stesso elemento di quelli che costituiscono il reticolo perfetto, che vanno a porsi negli interstizi (v. fig. 6B), sono sempre estremamente scarsi all'equilibrio termodinamico, se si eccettua il caso dei composti di quegli elementi piccoli o molto polarizzabili di cui si è detto sopra. Queste impurità possono essere prodotte, insieme a un egual numero di lacune, con trattamenti violenti, ad esempio mediante grandi deformazioni plastiche, il cui meccanismo non è stato ancora ben compreso, oppure in seguito a danni da irraggiamento; in questo caso un atomo del reticolo, urtato con forza sufficiente da una particella incidente o da un atomo primario del reticolo precedentemente spostato, può allontanarsi dal suo posto nel reticolo, prender posto in un interstizio lasciandosi dietro una lacuna e disporsi così in una posizione ‛autointerstiziale', detta anche di ‛doppio interstiziale' (split interstitial), allontanando con maggior forza dalla sua posizione uno degli atomi circostanti in modo da scaricare in parte la distorsione del reticolo (v. fig. 6C). L'atomo rimosso, per esser ben separato dalla sua lacuna, deve ricevere un'energia maggiore dell'‛energia di Wigner': questa è maggiore per circa un fattore 4 dell'energia di coesione per atomo e dipende fortemente dalla direzione, dato che gli interstiziali si creano molto più facilmente a distanza, se l'atomo, durante il suo moto, urta i vicini nella direzione di una fila compatta di atomi (effetto di focheggiamento).

Il danneggiamento ottenuto a bassa temperatura per irraggiamento con elettroni o ioni veloci è conosciuto piuttosto bene. Nel caso degli ioni bisogna tener conto del fatto che gli atomi del reticolo si schermano molto efficacemente l'uno con l'altro dall'azione degli ioni incidenti, nel caso in cui questi viaggino nel reticolo parallelamente a file atomiche compatte: questo processo di incanalamento permette agli ioni di piantarsi in profondità nel cristallo senza che questo venga eccessivamente danneggiato; questa possibilità viene tecnologicamente sfruttata per drogare localmente i semiconduttori.

Se gli atomi autointerstiziali sono difficili da produrre, essi sono tuttavia molto mobili, come la maggior parte degli interstiziali. Con energie di attivazione di solo una frazione di eV generalmente diffondono anche a temperatura inferiore a quella ambiente e, invero, la maggior parte degli autointerstiziali prodotti per irraggiamento si ricombina con le corrispondenti lacune. Se si aumentano sufficientemente le dosi di irraggiamento, si può tuttavia osservare la formazione di anelli di dislocazioni, dovuti all'agglomerarsi di difetti interstiziali, e di anelli di dislocazioni o di bolle, creati dall'agglomerarsi di lacune. Nei materiali anisotropi, come per esempio nell'uranio, le lacune e le impurità interstiziali si accumulano lungo differenti piani cristallografici; questo effetto provoca un allungamento del cristallo proporzionale alla radiazione, purché questa sia inviata in dosi massicce.

I problemi posti dalle tecnologie spaziali e nucleari (reattori nucleari), relativi al danneggiamento causato dalle tracce di fissione e dai neutroni veloci, sono compresi molto meno bene. Da molto tempo è noto che i solidi radioattivi si disintegrano quando, geologicamente parlando, sono sufficientemente vecchi. La loro età può appunto essere determinata misurando la densità delle tracce di fissione. Alcuni degli effetti che si producono in un reattore possono risultare utili: ad esempio sono state prodotte in questa maniera alcune leghe di NiFe in uno stato ordinato di alta durezza magnetica e, come si dirà in seguito, sono stati introdotti centri di colore nel diamante, che ha assunto una rara colorazione gialla. Ma i difetti puntiformi vengono prodotti localmente in grandi quantità e a distanza troppo ravvicinata per poter essere trattati separatamente. Le strutture disordinate che si ottengono in questa maniera lungo le tracce di fissione o al termine delle traiettorie dei neutroni veloci (cascate di collisioni) sono tuttora piuttosto mal conosciute. Le cascate di collisioni probabilmente fungono da centri di formazione di quelle bolle di gas di fissione che si osservano nei reattori veloci e che producono quei rigonfiamenti che attualmente costituiscono uno dei fattori limitativi degli stessi reattori.

Infine va anche messo in evidenza che, per quanto plausibile, l'analisi consueta dei movimenti degli atomi basata sulla teoria classica della velocità di reazione è approssimata: in essa si assume che alcuni effetti quantistici possano essere trascurati, ipotesi questa che sembra effettivamente vera, a parte casi eccezionali (moto degli atomi di idrogeno in alcuni metalli, precessione dinamica di Jahn-Teller delle impurità); generalmente si suppone anche che il reticolo assuma una pòsizione di equilibrio intorno all'atomo saltato via, e questa è una approssimazione molto più incerta, la cui validità è stata analizzata solo di recente con modelli simulati al calcolatore; inoltre i moti dovuti all'azione di un gradiente termico (‛effetto Soret') pongono numerosi e delicati problemi sia sperimentali che teorici tuttora non completamente chiariti.

Dislocazioni. - Le ‛linee di dislocazione' sono state i primi difetti lineari cui si sia pensato per spiegare le proprietà plastiche di un cristallo. A temperature basse o moderate, il fenomeno dello scorrimento viscoso dovuto alla diffusione delle lacune è trascurabile: il cristallo si deforma solo sotto uno sforzo finito, che superi il valore del limite elastico σ_c, variabile entro intervalli molto ampi, a seconda del tipo di cristallo, dei suoi difetti e della temperatura. In questo ambito le deformazioni avvengono per slittamento di parti del cristallo rispetto ad altre, lungo direzioni di scorrimento ben definite e cristallograficamente semplici, e spesso anche lungo piani ben definiti. Tutto questo suggerisce, e una dettagliata analisi lo conferma, che le due parti del cristallo tra le quali è avvenuto lo scorrimento, una volta che questo sia cessato, si trovino nuovamente con gli atomi in posizioni coerenti. Tuttavia, per poter produrre simultaneamente uno scorrimento su un'area finita si dovrebbero produrre deformazioni lungo il piano di scorrimento maggiori del 20%, cioè sforzi di taglio più grandi di 0,2 μ se μ è il modulo di taglio. Questo ‛sforzo di Frenkel' supera il valore di 10³ kg/mm², supera, cioè, di molto i limiti elastici osservati nella maggior parte dei cristalli, in particolare metallici, ionici e molecolari. Di qui l'idea che lo scorrimento non avvenga simultaneamente su un'area finita, ma piuttosto che si propaghi lungo i piani di scorrimento. Il difetto lineare che separa la parte del piano che ha già subito lo scorrimento da quella che non lo ha ancora subito viene chiamata ‛linea di dislocazione' (v. fig. 7A). Per spiegare i bassi valori dei limiti elastici osservati bisogna pensare che queste linee si muovano molto facilmente lungo i loro piani di scorrimento PP′. Questo sforzo di attrito solido, detto ‛sforzo di Peierls', non è stato calcolato con assoluta certezza per nessuna struttura cristallina; tuttavia, in tutte le strutture compatte in cui le forze sono sostanzialmente forze centrali, come ad esempio nei metalli, nei solidi ionici e nei gas rari, probabilmente è troppo piccolo per poter essere osservato. Nelle strutture covalenti, aventi legami fortemente direzionali, invece, lo scorrimento, per prodursi, deve prima rompere e poi ripristinare questi legami e quindi lo sforzo di Peierls risulta molto maggiore e attivabile termicamente.

Le linee di dislocazione possono venir definite, in tutta generalità, come linee di singolarità nel campo delle deformazioni interne di un cristallo deformato. È chiaro che linee di questo tipo possono venir collegate con uno spostamento relativo qualsiasi di due parti del cristallo, che appartenga alle sue trasformazioni di simmetria: cioè non solo una traslazione di b, ‛vettore di Burgers' (v. fig. 7A), ma anche una rotazione di ϑ (v. fig. 7C),o una combinazione di una rotazione e di una traslazione. L'energia necessaria per creare una simile linea di dislocazione è dovuta principalmente alle deformazioni a lungo raggio nel reticolo ed è quindi più o meno proporzionale al quadrato di b o di ϑ. Nel primo caso, la ‛tensione lineare', cioè l'energia per unità di linea, è circa dell'ordine di μb²: è quindi molto grande, se si pensa che anche per il valore di b più piccolo possibile, cioè per b eguale alla distanza interatomica lungo la linea, si ha μb³ ???54??? 5 eV. Le dislocazioni con rotazione (dette anche ‛disclinazioni') hanno tensioni lineari ancor più elevate, dato che le deformazioni a lungo raggio che esse provocano nel cristallo decrescono ancora più lentamente.

Pertanto si può dire che: 1) nei cristalli sono presenti solo dislocazioni di traslazione; dislocazioni rotazionali si sono osservate solo nei cristalli liquidi, nei quali gli sforzi possono parzialmente attenuarsi a causa della posizione disordinata delle molecole; 2) solo le dislocazioni con b dell'ordine delle dimensioni atomiche sono (meta)stabili, le altre si decompongono rapidamente in queste in modo da ridurre l'energia elastica accumulata; 3) in molte strutture, e in particolare in tutte quelle strutture semplici che caratterizzano i solidi ‛forti', ma anche in numerose altre più complesse, dislocazioni L perfette aventi b eguale a un periodo elementare del reticolo di Bravais si dividono in una coppia di dislocazioni imperfette L′ e L′′ aventi vettori di Burgers b′ e b′′ più piccoli e tali che b′ + b′′ = b. Lo scorrimento che li produce crea in mezzo ad essi un nastro di difetti, detto di ‛ammassamento' (v. S in fig. 7B). Questo è il motivo per cui le direzioni di h coincidono sempre con direzioni molto compatte del reticolo di Bravais e per cui spesso anche i piani di scorrimento sono piani compatti disposti lungo le direzioni dei possibili difetti da ammassamento; 4) la tensione lineare è talmente intensa che le dislocazioni non possono essere in alcun caso in equilibrio termico con il reticolo, anche se la loro presenza aumenta di una certa quantità l'entropia del cristallo abbassando localmente le frequenze delle vibrazioni atomiche. In effetti, questa tensione lineare è talmente elevata che per creare un anello di dislocazioni in un cristallo perfetto è necessario applicare uno sforzo enorme, paragonabile a quello di Frenkel. Quindi le dislocazioni in un cristallo si possono formare in seguito alla concentrazione di sforzi all'interno (gradini superficiali, precipitati con bordi netti) o, più spesso, durante la crescita dello stesso cristallo; è molto difficile infatti riuscire a produrre cristalli con meno di 10⁵ dislocazioni per cm², dato che la loro presenza può servire ad attenuare gli sforzi elastici a lunga distanza prodotti nei cristalli da gradienti di temperatura o di purezza.

Le deformazioni plastiche a bassa temperatura tendono ad aumentare la densità ρ delle dislocazioni, attraverso un processo che non è del tutto chiaro. Lo scorrimento delle dislocazioni viene così ostacolato e il cristallo viene indurito di un termine dell'ordine di 0,2μbρ^-1/2. Non esiste tuttavia un modello convincente che spieghi perché le dislocazioni aumentino all'aumentare delle deformazioni, nè il fatto che questo aumento è più rilevante nel caso della maggior parte delle strutture cubiche, in cui dislocazioni con differenti vettori di Burgers e differenti piani di scorrimento possono combinarsi per formare le ‛barriere di Cottrell', che sono immobili perché si suddividono su due piani di scorrimento differenti contemporaneamente. Inoltre l'indurimento è sempre maggiore nella direzione in cui sono stati applicati gli sforzi durante il procedimento che nelle altre: questo effetto, detto ‛effetto Bauschinger', indica che il reticolo delle dislocazioni non può venir descritto facendo uso solamente della densità media ρ. Finora non è stato possibile estrarre dalla descrizione microscopica dello scorrimento per dislocazioni tutti i parametri necessari per analizzare il meccanismo delle complesse deformazioni che avvengono su scala macroscopica.

Una linea di dislocazione L può ‛arrampicarsi' fuori del suo piano di scorrimento PP′ (v. fig. 7A) soltanto mutando il numero degli atomi sul semipiano atomico aggiuntivo LQ. Questo generalmente avviene per autodiffusione, quando cioè, a elevate temperature, le dislocazioni fungono da sorgenti o da punti di assorbimento efficienti per le lacune. Le lacune o gli autointerstiziali, se sono prodotti in condizioni di grande sovrassaturazione, possono anche precipitare all'interno del cristallo lungo piani compatti di atomi; una sezione di un disco di atomi mancanti prodotto da lacune precipitate appare come Q′L nella fig. 7; una sezione di un disco di atomi aggiuntivi prodottosi per precipitazione di autointerstiziali appare come QL: in entrambi i casi il bordo del disco forma un anello L di dislocazioni.

In generale i trattamenti termici riducono la durezza dei materiali precedentemente sottoposti a indurimento. Questo può avvenire per ‛riassestamento', cioè per mutuo annullamento e riordinamento delle dislocazioni che si muovono, oppure per ‛ricristallizzazione', cioè attraverso la crescita di cristalli più perfetti in cui i bordi dei grani spazzano via le dislocazioni. In alcune leghe, tuttavia, un trattamento termico di questo tipo produce un fenomeno di precipitazione fine che fissa le dislocazioni e quindi aumenta la durezza (ad es. carburi e nitruri negli acciai, zone di Guinier-Preston formate da atomi disciolti in duralluminio). Infine, negli scorrimenti a temperatura elevata si formano delle deformazioni sotto l'azione di sforzi costanti: questo fenomeno diventa importante quando la velocità di riassestamento e quella di indurimento per lavorazione diventano comparabili.

Superfici. - I materiali cristallini, in quanto limitati, possiedono sempre una ‛superficie esterna'. Se si tratta di un policristallo, cioè di una struttura composta da più di un cristallo, i grani cristallini costitutivi, aventi orientazioni differenti ed eventualmente natura differente, aderiscono reciprocamente lungo i bordi dei grani. Per certe coppie di cristalli si può definire un reticolo comune, o quasi comune, bidimensionale oppure tridimensionale, che consente a parte degli atomi sui due lati di trovarsi in posizioni tra loro coerenti; se i periodi del reticolo comune sono di dimensione atomica, questi bordi coerenti hanno un'energia particolarmente bassa: si ha un bordo ‛gemello' se i due cristalli hanno la stessa struttura, uno ‛epitassiale' in caso contrario (v. fig. 8). Sia la teoria che gli esperimenti di microscopia a emissione ionica mostrano in maniera convincente come la struttura atomica di ogni cristallo venga perturbata in effetti molto lievemente dalla presenza di queste superfici. Questo fenomeno è dovuto alla distanza estremamente corta che caratterizza l'ordine delle interazioni tra gli atomi.

Tutte queste superfici presentano una ‛tensione superficiale' definibile come il lavoro necessario per creare una superficie di area unitaria all'interno di un materiale cristallino perfetto e infinito. Nel caso di superfici libere, se ne può fare una stima contando il numero di legami interatomici interrotti, e risulta quindi dell'ordine dell'energia di coesione per area atomica. Naturalmente la tensione superficiale dipende dalla levigatezza della superficie e, nel caso di superfici che siano lisce su scala atomica, dalla loro orientazione rispetto al reticolo cristallino. Dopo trattamenti a temperatura elevata in vuoto ultraspinto, le superfici dei cristalli liberi tendono a divenire piane e a disporsi lungo piani compatti di atomi, con qualche gradino e qualche atomo o lacuna aggiuntivi (v. fig. 8A). Questi due ultimi difetti sono molto mobili e sono responsabili di gran parte dei fenomeni di trasporto veloce di materia, per diffusione, lungo le superfici. In realtà le superfici che si incontrano più comunemente sono in pratica sempre coperte di impurità adsorbite, oppure di uno strato di prodotti di reazione dovuto all'azione dell'atmosfera (per es. uno strato di ossido nei metalli).

L'agitazione termica degli atomi sulle superfici libere, che hanno una temperatura di Einstein più bassa, è più elevata di quella degli atomi che si trovano all'interno del cristallo ed è ancora maggiore per gli atomi aggiuntivi o siti lungo i gradini superficiali che per quelli siti su una superficie liscia. Le oscillazioni più intense possono essere osservate mediante diffusione di elettroni, i quali, quando hanno un'energia inferiore a 100 eV, analizzano solamente i primissimi strati di atomi. In particolari circostanze, la diminuzione di velocità delle onde elastiche, dovuta alle superfici libere, può portare alla formazione di modi di Rayleigh localizzati vicino alla superficie. Si fa comunemente uso di modi ultrasonori di questo tipo per analizzare il grado di levigatezza macroscopica della superficie; se ne studiano anche le applicazioni in teoria delle comunicazioni. Questi modi superficiali ovviamente sono molto sensibili alle variazioni subite dalle condizioni al contorno su dimensioni confrontabili con la lunghezza d'onda o la profondità di penetrazione. La presenza di uno strato superficiale meno rigido può dar luogo alla propagazione di ‛onde di Love' localizzate entro lo strato.

Nei solidi amorfi e nei liquidi possono, infine, formarsi superfici libere o di contatto aventi proprietà molto simili a quelle dei cristalli. In complesso però il loro studio è stato approfondito di meno, se si eccettua ciò che riguarda la misura delle tensioni superficiali. Un particolare problema caratteristico dei liquidi molecolari e dei cristalli liquidi è quello dell'effetto prodotto dalle condizioni al contorno sull'orientazione delle molecole: si tratta di un problema ancora non studiato in maniera sistematica.

5. La struttura elettronica.

a) Origine dell'ordine. Intensità fisico-chimica del legame.

Per studiare più in profondità la natura della materia bisogna giungere al livello elettronico. Si possono fare alcune osservazioni generali sui tipi di legame prima ancora di entrare in più precisi dettagli su alcune vaste classi di problemi che nascono dallo studio della materia allo stato condensato.

Nei solidi elementari e in alcuni composti semplici si possono individuare i principali tipi di legame.

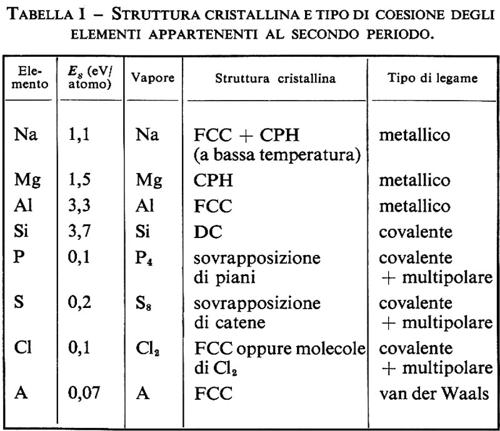
1. Seguendo una riga della tavola periodica degli elementi si possono osservare tutti i possibili tipi di legame dei solidi ‛elementari'. Per es., nella tab. I vengono richiamate le proprietà caratteristiche degli elementi della seconda riga. I primi quattro sono caratterizzati da elevate energie di sublimazione E_s (l'energia di sublimazione è l'energia necessaria per passare da cristallo a vapore) e da vapori allo stato atomico. Ogni atomo quindi è legato fortemente a quelli circostanti di modo che il cristallo nel suo insieme può venir considerato come una singola macromolecola. Negli ultimi quattro le molecole del vapore sembrano mantenere parte della loro individualità, dato che l'energia E_s necessaria per separarle è dell'ordine di 0,1 eV/atomo, molto minore dell'energia di legarne all'interno delle singole molecole, che è invece dell'ordine di 1 eV/atomo. Si può dare una spiegazione quantitativa di queste differenze facendo uso di concetti chimici approssimati.

Nell'argon, che è un ‛gas raro', gli atomi hanno simmetria sferica e livelli di valenza s²p⁶ pieni. A distanze d grandi sono quindi perfettamente neutri, interagiscono solamente mediante deboli ‛forze attrattive di van der Waals' a lungo raggio (che dipendono da d^-6), dovute a mutua polarizzazione (cioè a una correlazione tra gli elettroni di valenza), e, a breve distanza, mediante una intensa ‛forza di scambio' repulsiva, che impedisce il verificarsi di estese sovrapposizioni dei livelli pieni, in conformità col principio di esclusione di Pauli. I gas rari hanno quindi strutture non molto stabili, ma compatte: cubiche a facce centrate (FCC, da face centered cubic) nel caso dell'argon, in cui gli atomi si trovano sui vertici e al centro delle facce di un cubo (v. fig. 9A), e esagonali compatte (CPH, da dose packed hexagonal) negli altri, aventi strutture compatte con simmetria esagonale (v. fig. 9B).

Il cloro, lo zolfo e il fosforo formano tre tipi di ‛cristalli molecolari' che presentano legami ‛covalenti' all'interno di ciascuna molecola e solo deboli attrazioni elettriche di multipolo (e forze di scambio repulsive a corto raggio) fra molecola e molecola. Come al solito, i legami covalenti si costruiscono mediante una forte sovrapposizione di orbitali molecolari ottenuta tramite una combinazione lineare di orbitali atomici: un orbitale p per il cloro (che dà un legame per atomo e quindi crea molecole di Cl₂ che formano pile compatte in un reticolo FCC, come nella fig. 10A), due orbitali sp² ‛ibridizzati' nel caso dello zolfo (che danno due legami per atomo disposti a circa 120° e formano quindi catene che si chiudono in anelli di S₈ nel caso del vapore o si incolonnano in lunghe catene parallele elicoidali nei cristalli, come nella fig. 10B), tre orbitali sp² nel fosforo (che portano a tre legami per atomo complanari e quindi producono nel vapore molecole di P₄ che si legano nel cristallo per formare piani esagonali paralleli, come nella fig. 10C).

Il silicio forma cristalli ‛covalenti', in cui ogni atomo crea quattro legami mediante quattro orbitali sp² ibridizzati. Questi legami sono orientati secondo le direzioni dei vertici di un tetraedro e rendono quindi possibili strutture covalenti tridimensionali; la più simmetrica di queste strutture è quella cubica propria del diamante (DC, da diamond cubic), che può essere pensata come un reticolo FCC di molecole C₂ covalenti (v. fig. 10D); la si osserva in tutti i solidi tetravalenti (C, Si, Ge e Sn grigio).

Ci si potrebbe aspettare che Al, Mg e Na presentino strutture cristalline molecolari analoghe a quelle del P, dell'S e del Cl rispettivamente, ma i corrispondenti legami covalenti sono più deboli, per via del maggiore raggio degli orbitali, in conseguenza del fatto che la carica dei nuclei è più piccola. Si presenta quindi un'altra configurazione: ogni atomo è circondato da un grande numero di atomi vicini posti a una distanza sufficientemente piccola perché vi sia un'intensa sovrapposizione di orbitali atomici. Ogni elettrone di valenza può quindi rapidamente saltare da un legame di valenza a un altro attraverso l'intero cristallo. I 'legami metallici' sono appunto caratterizzati da questo fenomeno di delocalizzazione. Nei metalli qui considerati gli elettroni sp si comportano all'incirca come elettroni liberi; la coesione è dovuta essenzialmente all'attrazione coulombiana tra questo gas di elettroni liberi e gli ioni positivi all'interno del reticolo, tanto è vero che, per lo meno a basse temperature, si presentano semplici strutture compatte (FCC, CPH). Strutture simili, anche se lievemente meno compatte, come, ad esempio (v. fig. 9C), quella cubica a facce centrate (BCC, da body centered cubic), si osservano nei metalli di transizione dei periodi più elevati, dove gli stati d, solo parzialmente pieni, creano una delocalizzazione più debole e un legame covalente più intenso. Nei metalli delle terre rare, gli orbitali f che sono solo in parte riempiti, praticamente non si sovrappongono e danno quindi uno scarso contributo alla coesione.

2. Nei composti semplici, oltre alle precedenti strutture metalliche covalenti e molecolari, si trovano due ulteriori tipi di legami.

La struttura a ‛legame ionico', con ioni di segno opposto alternati e appartenenti a colonne molto distanti della tavola periodica (come nel caso del sale da cucina: Na⁺Cl^-), è caratterizzata da forti interazioni elettrostatiche che portano a grandi energie di coesione, maggiori di un eV per atomo (v. fig. 11A).

Nelle strutture a ‛legame idrogeno' un protone risuona tra due atomi o tra due radicali identici ai quali può cedere il suo elettrone (v. fig. 11B). L'incremento di energia, come in un legame elettronico, è dell'ordine di ℏω/2, dove ω è la frequenza del protone risonante. La particolare efficienza dell'idrogeno in questo tipo di legame deriva dal fatto che le frequenze di vibrazione diminuiscono all'aumentare della massa atomica risonante. Ma, anche per il protone, è ω ???60??? 10¹⁴ s^-1 e quindi l'energia di legame al massimo è di qualche decimo di eV. È questa la causa delle temperature piuttosto basse di fusione e di ebollizione dell'acqua.

Questa sia pur sommaria descrizione della struttura elettronica degli atomi può dar ragione delle caratteristiche principali che si osservano nelle varie strutture atomiche e dell'ordine di grandezza delle forze di coesione nei principali tipi di cristalli. Tre principali tipi di legami, e le loro mescolanze, portano a grandi energie di coesione: il legame metallico, quello covalente e quello ionico. Le proprietà di questi solidi ‛forti' sono state studiate con maggior dettaglio rispetto a quelle dei solidi più ‛deboli', con legami multipolari, di van der Waals o a idrogeno. Questi ultimi tuttavia costituiscono un fertile campo di ricerca di crescente interesse.

In ultima analisi, fatta eccezione per i legami covalenti, la coesione dipende in massima parte dalla vicinanza degli atomi (o degli ioni) tra di loro, più che dai dettagli della loro relativa disposizione, tanto è vero che è facile osservare cambiamenti di fase con calori latenti piccoli: lo stesso calore necessario per la semplice fusione è molto minore dell'energia di sublimazione. Così, nei metalli, nei composti ionici e negli aggregati molecolari, ci si devono aspettare strutture elettroniche all'incirca simili in tutte le fasi cristalline, amorfe e liquide. In generale, la fusione distrugge i legami puramente covalenti favorendo invece legami metallici, anche se sono geometricamente possibili e riscontrabili nello stato solido strutture amorfe di atomi legati in maniera quasi perfetta da legami tetragonali.

b) Strutture a bande elettroniche nelle fasi condensate.

1. Per analizzare le onde di eccitazione degli elettroni nei solidi si possono usare più o meno gli stessi metodi descritti nel caso delle onde elastiche; ciò almeno è corretto per il caso di quei solidi che prima abbiamo chiamato forti, nei quali gli atomi sono legati gli uni agli altri così intensamente da formare un'unica macromolecola attraverso la quale gli elettroni di valenza si spostano molto rapidamente, più o meno come gli elettroni di un plasma gassoso. Così, nella prima ‛approssimazione di Hartree-Fock', si può supporre - come si fa nel caso dei plasmi - che ogni singolo elettrone si trovi nel potenziale elettrico dovuto a tutti gli altri, mediato nel tempo. Si può inoltre trascurare il moto dei nuclei, in quanto molto più pesanti (approssimazione ‛adiabatica'). Tutti gli elettroni si muovono quindi nel medesimo potenziale medio reticolare Ã, che in generale si può scomporre nei singoli contributi atomici V_j:

Così, in uno stato stazionario, le loro funzioni d'onda ψ di energia E sono autofunzioni della medesima hamiltoniana per un elettrone H = (ℏ²/2m)∆ + Ã:

Hψ = Eψ. (13)

Portando avanti i calcoli si trova che gli stati atomici di bassa energia, corrispondenti agli orbitali atomici più interni, si aprono a formare strette ‛bande' di stati energetici permessi, ben separate tra di loro da salti di energia (gaps); gli stati atomici eccitati danno invece luogo a una banda di energia che varia con continuità da un limite inferiore fino all'infinito. La distribuzione di questi stati può essere specificata assegnando la densità n(E) per unità di energia e di volume. Secondo la statistica di Fermi, gli elettroni più interni occupano le bande più interne, due per stato con spins opposti, mentre gli elettroni di valenza vengono a trovarsi in una condizione intermedia: nella maggior parte dei legami, cioè in quelli covalente, ionico, molecolare e di van der Waals, gli elettroni di valenza riempiono una ‛banda di valenza', che è separata dalle bande vuote superiori da un salto finito di energia; nei metalli essi riempiono invece la parte più bassa di una banda superiore che è continua. Si possono comprendere questi risultati semplicemente estendendo il concetto degli orbitali molecolari, di uso comune nel caso delle molecole più piccole. Si consideri ad esempio una fase condensata costituita dal medesimo tipo di atomi, tutti circondati più o meno alla medesima distanza dagli atomi più vicini. I livelli atomici più interni con orbitali ψ_i, i cui raggi non siano troppo grandi rispetto alle distanze interatomiche, danno luogo a bande di energia le cui funzioni d'onda possono essere approssimativamente scritte come una combinazione lineare delle ψ_j:

Esistono tante combinazioni lineari indipendenti quanti sono gli orbitali ψ_j nel campione. In quella più stabile, le a_j sono tali che le ψ_j della maggior parte, se non di tutte, le coppie jl di due atomi contigui sommano le loro ampiezze in ψ; l'energia dello stato ψ sarà quindi, per ogni legame jl, l'energia E_B dello stato legato per la molecola biatomica (ψ_j, ψ_l). Nello stato più instabile, invece, le a_j sono fatte in modo che le ampiezze della maggior parte delle coppie interatomiche di atomi contigui si sottraggano: l'energia di ψ per ogni legame jl sarà quindi l'energia E_AB dello stato antilegato della molecola biatomica. Tra questi limiti estremi si possono ricavare, uno dopo l'altro, tutti gli stati, ciascuno dei quali si ottiene da uno di energia più bassa, rispetto al quale è ortogonale, cambiando i segni dei coefficienti a_j relativi a una parte del volume totale V ≃ L³, limitato da una superficie S ≃ L²: i due stati successivi hanno in media una energia per legame che differisce al più di

se a³ è il volume medio per legame. Nel caso quindi di campioni macroscopici (L ≫ a), gli stati permessi formano una banda di energia quasi continua, di larghezza ℏω = E_AB − E_B comparabile con l'energia di legame delle molecole biatomiche che si possono costruire con due orbitali atomici; analogamente alle molecole più semplici, ω dà la frequenza media con cui oscillano tra i vari atomi gli elettroni della banda. La larghezza della banda, inoltre, come nel caso delle molecole, è dell'ordine degli integrali di sovrapposizione 〈ψ_j ∣ V_l ∣ ψ_l> e varia quindi esponenzialmente con il raggio a degli orbitali atomici e con la distanza interatomica l.

Nei solidi ionici e nei gas rari il rapporto a/l è sufficientemente piccolo, fino agli stati di valenza, perché questa LCAO (da Linear Combination of Atomic Orbitals, o combinazione lineare di orbitali atomici) o ‛approssimazione di legame stretto' valga per tutti gli elettroni della materia allo stato condensato nel loro stato stabile; gli orbitali atomici pieni danno origine a bande piene con un egual numero di stati. Lo stesso accade nei metalli di transizione fino agli elettroni d di valenza che sono caratteristici di questi metalli; ma, dal momento che gli orbitali d sono solo parzialmente riempiti, anche la banda d non è riempita del tutto; inoltre l'approssimazione non può essere applicata agli elettroni di valenza sp. Nelle strutture covalenti si deve tener conto, analogamente a quanto si fa nel caso delle molecole più semplici, della forte ibridizzazione sp che mescola le bande s e p ma separa la parte di legame da quella di antilegame; si può quindi pensare che la banda di valenza leghi stati sp di molecole biatomiche, che, allargati dalle loro combinazioni lineari, permettono agli elettroni di saltare da un legame all'altro nel cristallo; la banda di valenza contiene perciò tanti stati quanti sono i legami sp che la formano ed è quindi piena nelle strutture covalenti.

Questo tipo di analisi richiede solo che ci sia un ordine a breve raggio e si può quindi applicare tanto ai cristalli quanto ai liquidi, ai solidi amorfi e alle leghe. Non è invece valido per stati energetici troppo elevati, ad esempio per gli stati eccitati degli isolanti o per gli elettroni di valenza sp nei metalli: questi stati possono essere generalmente considerati come pressoché liberi, soggetti solo debolmente a processi di diffusione causati dal potenziale degli atomi.

2. In un ‛cristallo perfetto', Ã e quindi H sono periodici; come per le onde elastiche si può dunque prendere per ψ una funzione di Bloch

ψ = U_k (r) exp(ik • r), (15)

in cui U_k (r) ha il medesimo periodo del reticolo di Bravai 5 e il vettore d'onda k può variare in maniera quasi continua all'interno della prima zona di Brilbuin. I vari rami E(k) si susseguono in corrispondenza di stati atomici di energia crescente o di loro ibridi; ogni ramo crea una banda di stati di energia permessa in numero pari a quello delle celle elementari del cristallo.

Nello stato stabile a zero gradi assoluti, gli elettroni occupano tutti gli stati fino a quello corrispondente a una certa energia massima E_F. La funzione f(E) della ‛distribuzione di Fermi', che dà la probabilità che ha uno stato di energia E di essere occupato, diviene quindi una funzione gradino (di Heaviside), con un taglio netto (v. fig. 12, curva A). L'eccitazione di un singolo elettrone corrisponde quindi al suo trasferimento da uno di questi stati di energia E a uno di energia maggiore E + ΔΕ e alla formazione di una coppia elettrone eccitato n e lacuna positiva p. L'equilibrio chimico a una temperatura T diversa da zero,

0 ⇄ n + p + ΔΕ, (16)

dà, per la legge delle azioni di massa, valida in questo caso, dal momento che due elettroni non possono occupare il medesimo stato,

Si è tenuto qui conto del fatto che il fattore della distribuzione di Fermi per una lacuna positiva è 1 − f. Per ogni E e ΔE la soluzione di questa equazione è

dove il ‛livello di Fermi' E_F(T) è scelto in maniera tale che il numero totale degli elettroni sia indipendente da T. All'aumentare della temperatura, il gradino nella f(E) si allarga con una larghezza media kT e due code esponenziali (v. fig. 12).

Ci si aspetta una sensibile differenza nelle proprietà elettriche a seconda che E_F si trovi (v. fig. 13) o no (v. fig. 14) in una banda di energia permessa.

Nel primo caso si possono avere stati elettronici eccitati di energia molto bassa e velocità non nulle: il cristallo è un ‛conduttore metallico', la sua conduttività elettrica a 0 °K ha un valore non nullo e varia solo lentamente con la temperatura. La diffusione coerente degli elettroni di valenza da parte degli atomi del reticolo produce le onde di Bloch e dà ragione di come le curve di dispersione E(k) differiscano da quelle degli elettroni liberi; si comprende così il motivo della relativa stabilità delle varie fasi cristalline e delle loro costanti elastiche. La conducibilità elettrica σ, e quella termica K sono entrambe dovute allo spostamento dei portatori elettronici, il cui numero varia debolmente con la temperatura, dal momento che la distanza di E_F dal fondo E₀ della banda di valenza è generalmente grande rispetto a kT (v. fig. 13).

La conducibilità, quindi, è limitata solamente dalla diffusione incoerente delle onde di Bloch contro le impurità statiche e dinamiche, ad esempio le impurità atomiche oppure i fononi. La resistività elettrica ρ = σ^-1 risulta essere all'incirca data dalla somma di una parte dovuta alle impurità esterne, indipendente dalla temperatura, e di una parte intrinseca dovuta ai fononi, la quale, al di sopra della temperatura di Debye, aumenta linearmente con T. La maggior parte delle altre proprietà di trasporto e anche le principali proprietà magnetiche possono essere ricondotte alla struttura elettronica E(k) vicino alla superficie di Fermi a 0 °K: E(k) = E_F. Questa struttura è stata analizzata piuttosto compiutamente seguendo vari procedimenti basati in generale sulla rotazione degli elettroni intorno a un campo magnetico fisso, con un'accelerazione usualmente fornita da un campo elettromagnetico di frequenza compresa nello spettro radio o infrarosso, o da un'onda acustica. Queste misure hanno mostrato come sia grande la varietà e la complessità delle forme possibili assunte dalle superfici di Fermi nello spazio reciproco e inoltre hanno confermato le regolarità previste dai semplici modelli a legame forte o a elettroni quasi liberi.

Nel secondo caso (v. fig. 14) l'energia minima di eccitazione degli elettroni è pari alla larghezza l dell'intervallo proibito. Il cristallo si comporta a basse temperature come un isolante con un campo critico di rigidità elettrica, che corrisponde a un effetto tunnel attraverso l'intervallo proibito tra le bande e che quindi deve essere elevato e deve aumentare con l. In alcuni cristalli, come ad esempio il Si o il Ge, l non è molto grande in rapporto all'energia termica a temperatura ambiente e di conseguenza ci si aspetta che la conducibilità elettrica aumenti esponenzialmente con la temperatura nello stesso modo del numero dei portatori n nella banda di conduzione c quasi vuota o del numero dei portatori p, che sono sempre quelli più mobili, nella banda di valenza quasi vuota.

L'equilibrio chimico

0 ⇄ n + p + l (eV)

dà

In altre parole, il livello di Fermi E_F cade nel mezzo dell'intervallo tra le bande.

Il corrispondente fenomeno, per il quale si ha un forte aumento di σ con la temperatura T, è caratteristico di un ‛semiconduttore' (intrinseco). La struttura elettronica (intervallo l tra le bande, forma di E(k) vicino all'estremo superiore della banda di valenza e a quello inferiore della banda di conduzione) propria di vari semiconduttori e isolanti tipici è stata analizzata sia con metodi ottici, sia facendo uso di tecniche di risonanza, uguali a quelle usate per i metalli. In maniera simile si sono osservate variazioni regolari con la valenza e il periodo.

3. Come già si è messo in evidenza, la distinzione tra isolanti e conduttori è essenzialmente dovuta all'ordine su brevi distanze, caratteristico della fase condensata. Così, gli isolanti mantengono nelle fasi amorfe solide o liquide una banda di valenza ben separata in energia da una banda di conduzione se, come succede usualmente, l'energia necessaria per rompere i legami covalenti o per ionizzare gli ioni negativi (oppure gli atomi neutri dei gas rari) è grande in confronto con il calore di fusione. Fanno eccezione, com'è noto, il Si e il Ge, che danno luogo a liquidi metallici con struttura compatta, anche se nella fase solida amorfa covalente sono semiconduttori; altre strutture covalenti, quali ad esempio quelle del Se o del Te, mantengono le loro catene covalenti semiconduttrici nei solidi amorfi a bassa temperatura o nei liquidi sottoraffreddati, ma a temperature più elevate i loro legami diventano metallici. In tutte queste strutture isolanti, la banda di valenza in generale può venir descritta con la stessa approssimazione di legame forte che si usa per la fase cristallina; ma le proprietà precise di mobilità dei portatori presso i bordi delle bande di valenza e di conduzione, e quindi le corrispondenti proprietà di trasporto, sono ancora oggetto di discussione. D'altra parte, la banda di conduzione tanto nelle fasi isolanti quanto nei normali metalli può essere ancora descritta con buona approssimazione facendo uso di un modello a elettroni quasi liberi, debolmente diffusi da atomi disposti in maniera quasi casuale.

c) Critiche alle principali approssimazioni introdotte nello studio delle strutture elettroniche.

Mentre si procedeva all'analisi sistematica delle proprietà generali di un cristallo perfetto, secondo lo schema precedentemente delineato, si è sviluppato un notevole interesse per una revisione critica delle principali assunzioni di base. Oltre a promuovere lo studio delle imperfezioni, che descriveremo in seguito, questa revisione ha portato a un'analisi dei possibili tipi di accoppiamento tra le diverse eccitazioni atomiche ed elettroniche. La complessità caratteristica delle tecniche che si usano in questi problemi a ‛molti corpi' è dovuta appunto al gran numero di queste eccitazioni.

Accoppiamenti tra elettroni e fononi. Superconduttività. - Gli accoppiamenti tra elettroni e fononi sono ovviamente più intensi nei solidi ionici, in cui la carica degli elettroni interagisce con quella degli ioni. Gli accoppiamenti di ‛polarone' che ne derivano modificano in maniera rilevante la mobilità degli elettroni e delle lacune positive. Un portatore elettronico in moto quindi è circondato da una nube di polarizzazione ionica che può venir analizzata in termini di fononi ottici; in altre parole, il suo potenziale coulombiano Σ_i Z_ie²/(ε ∣ r − R_i ∣) di interazione con gli ioni del reticolo risulta schermato da una costante dielettrica ε che, per frequenze minori di ω₀ (v. fig. 3), contiene un contributo quasi statico dovuto allo spostamento degli ioni. Come nel caso descritto nella fig. 4, si presentano effetti di risonanza nel caso in cui sia i vettori d'onda dei portatori elettronici, sia le loro energie cinetiche siano vicini a quelli dei fononi ottici: questo è il così detto regime a ‛polaroni forti'. Nel caso di portatori più veloci, la polarizzazione degli ioni produce solamente un leggero aumento della loro massa effettiva, aumento che può venir trattato con metodi perturbativi (regime a ‛polaroni deboli'). In certi casi può accadere che portatori più lenti causino delle distorsioni del reticolo sufficientemente grandi da non poter più essere trattate con i metodi dell'approssimazione elastica. A questo punto i portatori possono restare ‛autointrappolati': la distorsione locale è talmente marcata da renderne molto improbabile una modificazione attraverso il movimento di punto zero degli ioni; il moto dei portatori è allora più che altro dovuto a salti termici, durante i quali essi assorbono energia da un fonone locale e la trasferiscono per ‛effetto tunnel' da un sito polarizzato (uno ione oppure una molecola) a uno vicino non polarizzato. Si possono osservare lacune positive autointrappolate in coppie di ioni di alogeni in tutti gli alogenuri alcalini: la conduzione a basse temperature in composti isolanti di transizione, come ad esempio il Fe₂O₃, è dovuta ai salti degli elettroni d tra due ioni di transizione vicini.

Gli accoppiamenti tra elettroni e fononi non possono essere trascurati nei semiconduttori e nemmeno nei conduttori metallici, in quanto lo schermaggio da parte del gas elettrico non è un fenomeno locale, ma si estende su una distanza dell'ordine della lunghezza d'onda λ_F corrispondente al livello di Fermi. In altre parole, la costante dielettrica di un conduttore dipende dal numero d'onda k = 2π/λ della perturbazione e diviene piccola quando è k > k_F. Ne segue che le componenti di Fourier Ze²/ε(k)k² dell'accoppiamento tra elettroni e ioni divengono importanti per k > k_F. Esse limitano la mobilità dei portatori elettronici ad alta temperatura, fanno sì che gli elettroni portino con sé i fononi e viceversa, dando luogo a forti anomalie nel potere termoelettrico, e regolano il trasferimento di energia tra gli elettroni e il reticolo quando gli elettroni sono eccitati da un forte campo elettrico (problemi di conduzione di elettroni ‛caldi'), dall'irraggiamento con particelle cariche, da fenomeni di risonanza elettronica, ecc.

Certamente l'aspetto più spettacolare di questi accoppiamenti è però offerto dalla ‛superconduttività', che si manifesta in molti metalli e leghe a bassissime temperature e per la quale praticamente sparisce ogni resistenza (v. criofisica). Attualmente si sa che questo fenomeno è in generale un effetto dell'accoppiamento tra elettroni e fononi: elettroni di Fermi che si spostano velocemente, con spins opposti e funzioni d'onda spaziali simmetriche per inversione temporale, tendono ad associarsi e a formare le cosiddette ‛coppie di Cooper', in modo da trarre il massimo beneficio dal loro accoppiamento con fononi lenti. L'energia 2Δ necessaria per separare una coppia di Cooper è una funzione crescente dell'accoppiamento elettrone-fonone; essa è però sempre piccola, sicché le temperature critiche T_c ≃ Δ/k, al di sopra delle quali l'effetto di superconduttività scompare, sono dell'ordine di 20 °K. L'estensione spaziale di una coppia, la cosiddetta ‛lunghezza di coerenza' ξ₀, è la lunghezza percorsa in un tempo ℏ/πΔ da un elettrone di Fermi con velocità v_F:

ξ₀ = ℏv_F/πΔ; (17)

essa varia in un ampio intervallo compreso tra 10 e 10⁴ Å.

Questo accoppiamento impedisce la diffusione incoerente dei singoli elettroni, che è responsabile della resistenza elettrica, e permette che la coppia si muova come un tutto unico, formando una corrente elettrica. Più precisamente, sia ϕ (... r_p ...) la funzione d'onda totale di un campione superconduttore nel suo stato stabile, in assenza di correnti j o di campi magnetici applicati h. Gli stati superconduttori ψ che permettono la formazione di correnti macroscopiche o la penetrazione da parte di un campo magnetico lentamente variabile possono essere costruiti nella forma

dove S(r) è una funzione delle coordinate spaziali che varia lentamente. La corrente elettrica macroscopica diviene allora

dove A è il potenziale vettore magnetico associato ad h e n(r) è la densità elettronica. Trascurando le oscillazioni di n(r) su distanze atomiche si ottiene l'equazione di London per le correnti macroscopiche:

Applicando questa equazione e quella di Maxwell, rot h = 4πj_S/c, alla superficie di un superconduttore, si vede che h deve essere tangente alla superficie e che può penetrare nel superconduttore solamente fino a una profondità

che è generalmente minore di 10³ Å. Campioni superconduttori macroscopici escludono dal loro interno campi magnetici di piccola intensità attraverso la creazione di una corrente di superficie ('effetto Meissner'; v. criofisica, cap. 4, È b). Tuttavia, per un certo intervallo di valori dei campi applicati, si possono avere stati misti in cui coesistono regioni superconduttrici e altre normali. Se una regione superconduttrice, con spessore maggiore di 2λ, circonda una regione normale di forma cilindrica dove è già penetrato il flusso magnetico, si può applicare l'equazione (19) a un circuito C tracciato internamente alla regione superconduttrice, tutt'intorno a quella normale; se il superconduttore è nel suo stato più stabile, in assenza di correnti di volume, lo sfasamento S(r) vale ΔS = eA/ℏc. L'integrale § di ∇S lungo C deve allora essere un multiplo di π:

dal momento che ψ deve essere una funzione a un solo valore e che Φ è costituita dalle funzioni delle coppie di elettroni che sono anch'esse a un sol valore, ma che possono avere un cambiamento di segno dovuto allo scambio degli elettroni di una coppia. Il flusso magnetico totale nella regione normale risulta così quantizzato e ogni quanto vale Φ₀ = hc/2e. Nei superconduttori di ‛seconda specie' la lunghezza di coerenza ξ₀ è piccola in paragone allo spessore di penetrazione λ; la maggior parte dell'energia di una linea di flusso è quindi racchiusa nello spessore di penetrazione ed è proporzionale a Φ² Per rendere minimo questo valore, ogni linea di flusso si divide spontaneamente in linee di flusso elementare (cioè di valore minimo Φ₀); queste linee di flusso (o linee di vortice della corrente superconduttrice j_S) tendono a disporsi insieme secondo lo schema di un reticolo triangolare regolare, ma vengono ostacolate nel loro moto da difetti di volume o di superficie; molte delle loro proprietà sono in effetti simili a quelle delle linee di dislocazione. Questi stati misti possono aversi per un ampio intervallo di variabilità dei campi applicati; alcuni di questi superconduttori, inoltre, hanno temperature critiche elevate e possono quindi essere utilizzati nella costruzione di magneti di grandi dimensioni o aventi elevati flussi. In effetti tutto il programma di ampliamento del CERN II è legato ai miglioramenti che si riuscirà ad apportare alle proprietà di isteresi di questi magneti.

Il flusso magnetico contenuto all'interno di un anello superconduttore C è quantizzato secondo la (22). Interrompendo l'anello con un sottile strato isolante e applicando opportune differenze di potenziale, si possono cambiare l'uno rispetto all'altro gli sfasamenti S₊ e S_- da entrambi i lati dello strato: questo corrisponde al passaggio attraverso la barriera, per effetto tunnel, di una corrente superfluida di coppie di Cooper. Si può dimostrare che questa corrente oscilla sinusoidalmente con S₊ − S_- e ogni oscillazione corrisponde al passaggio attraverso lo strato verso l'interno o verso l'esterno di un quanto di flusso. Questo effetto, detto ‛effetto Josephson', mostra in maniera diretta la coerenza macroscopica di un sistema quantistico puro e può essere usato per misurare differenze di potenziale estremamente basse o campi magnetici particolarmente deboli.

È ragionevole aspettarsi che in un futuro abbastanza vicino i superconduttori trovino altre applicazioni in elettrotecnica (motori, trasformatori e forse trasporto dell'elettricità); il loro impiego è limitato dalla necessità di usare basse temperature e dalle perdite per isteresi; inoltre i superconduttori perdono le loro proprietà caratteristiche alle alte frequenze, quando ℏω è più grande di Δ.

Accoppiamento elettrone-elettrone. Magnetismo. - Le forze tra elettroni all'interno degli atomi ostacolano il trasferimento degli elettroni da un atomo a un altro quando la distanza tra atomi o molecole equivalenti è grande rispetto alle dimensioni delle orbite elettroniche. Si spiegano in questa maniera le particolari proprietà degli orbitali f dei metalli delle terre rare e le caratteristiche isolanti dei composti ionici con ioni di transizione, i quali, secondo l'approssimazione a bande, dovrebbero essere conduttori (ad es. l'NiO). Particolarmente interessanti sotto questo riguardo sono anche gli ossidi degli elementi di transizione alla sinistra della tavola periodica, come ad esempio gli ossidi del vanadio, e altri composti, i quali sembrano capaci di passare, per effetto di piccole variazioni di temperatura, pressione e composizione, da uno stato di isolante strettamente correlato a uno più normale di conduttore ('transizioni di Mott'). Anche alcuni composti organici potrebbero presentare problemi simili.

Più in generale, bisogna tener conto degli accoppiamenti tra elettroni per analizzare correttamente la stabilità delle fasi condensate, specialmente nei metalli normali. Questi accoppiamenti danno anche luogo, analogamente a quanto avviene nei plasmi gassosi, a oscillazioni longitudinali del gas elettronico ('onde di plasma' e, in presenza di campi magnetici, ‛onde a elica' o ‛onde di Alfvén', a seconda del numero e del tipo dei portatori coinvolti). Queste eccitazioni sono quantizzate e possono dar luogo a interessanti fenomeni di risonanza e di assorbimento. Infine l'accoppiamento elettrone-elettrone giuoca un ruolo importante nelle proprietà ottiche dei solidi: negli isolanti, infatti, elettroni eccitati dalla banda di valenza (oppure da bande anche più interne) rimangono legati al campo coulombiano della lacuna positiva che si è formata; questo sistema, detto ‛eccitone', provoca un assorbimento a frequenze più basse di quella corrispondente alla differenza di energia tra le bande e può avere anche una certa influenza sul processo di ricombinazione tra elettroni e lacune. Inoltre, elettroni o lacune elettroniche creati con un'energia cinetica superiore all'intervallo tra le bande possono aver la vita media abbreviata da un ‛effetto Auger' per cui essi si diseccitano eccitando a loro volta altri portatori oltre l'intervallo proibito tra le bande. Questo processo è particolarmente efficiente nel caso di lacune profonde. Nei metalli non esistono eccitoni legati, ma, nelle transizioni da una banda a un'altra, l'interazione elettrostatica tra la lacuna e tutti gli elettroni di conduzione porta a correzioni negli spettri di emissione e di assorbimento che sono rilevanti solamente per le zone vicine agli estremi dell'assorbimento o dell'emissione e solamente nel caso che le lacune siano molto meno mobili degli elettroni. Può verificarsi un effetto Auger tra gli elettroni di valenza per tutte le eccitazioni con intervallo energetico δE = ∣ E − E_F ∣ degli elettroni e delle lacune; questo effetto causa una diminuzione della vita media τ, legata all'aumento del numero dei portatori di più basse energie di eccitazione, prodotto dalle eccitazioni stesse a causa del principio di esclusione: τ^-1 ∝ (δE)² per δE → 0 (numero dei portatori proporzionale a δE; probabilità di eccitazione al di sopra di E_F proporzionale a δE).

Probabilmente però gli effetti più spettacolari dell'accoppiamento tra elettroni sono quelli magnetici. È noto che le interazioni di scambio tra gli elettroni, dovute alle proprietà di antisimmetria delle loro funzioni d'onda, possono in certe condizioni portare alla formazione di momenti magnetici permanenti su vari atomi del solido accoppiati tra di loro in varie maniere. L'importanza pratica di questo argomento è stato il primo stimolo per la sua elaborazione.

A temperature elevate, generalmente, l'agitazione termica perturba l'ordine dei momenti magnetici, senza però distruggerli effettivamente (v. fig. 15A). Se si applica un campo magnetico h, questo produce un momento magnetico m, la cui intensità è proporzionale all'intensità di h, che aumenta al diminuire della temperatura T secondo la legge di Curie-Weiss

χ = m/h ≃ C/(T − T_p).

La costante di Curie C è proporzionale al momento degli atomi; la temperatura paramagnetica di Curie T_p fornisce una misura media dell'intensità dell'accoppiamento tra momenti magnetici vicini.

A basse temperature questi accoppiamenti inducono un allineamento spontaneo dei vari momenti. Si ha allora il ‛ferromagnetismo', quando all'interno di un dominio macroscopico tutti i momenti sono allineati (v. fig. 15B), oppure varie forme di ‛antiferromagnetismo' (v. fig. 15C) e di ‛ferrimagnetismo' (v. fig. 15D), quando i momenti atomici puntano in varie direzioni, in modo tale che il loro valor medio rispettivamente si annulli oppure sia diverso da zero.

In questo campo numerose applicazioni tecniche hanno fatto seguito a una ricerca di base particolarmente attiva, fondata inizialmente sulla misura di quantità macroscopiche e ora anche su tecniche di diffusione neutronica, sulla risonanza magnetica nucleare e sull'effetto Mössbauer. I fattori principali sono il valore dei momenti magnetici, il segno e l'intensità dei loro accoppiamenti, l'energia magnetocristallina (che spinge i vari momenti ad allinearsi parallelamente ad alcune direzioni cristallografiche) e il fattore demagnetizzante dovuto all'interruzione dell'induzione magnetica causata dalla superficie esterna. Tra le applicazioni sono da ricordare i magneti duri che sfruttano forti anisotropie magnetocristalline presenti in una struttura a simmetria uniassica, oppure piccoli fattori di demagnetizzazione in presenza di grani allungati; le ferriti cubiche e i granati usati come magneti a induzione (piccola anisotropia magnetocristallina); le sottili pellicole magnetiche impiegate come elementi di memoria.

Le principali caratteristiche del ciclo di isteresi dei materiali ferro- e ferrimagnetici possono essere bene comprese pensando alla creazione, sotto l'azione del campo applicato, di alcuni domini di ordine magnetico, che coesistono anche in mancanza di un campo esterno, i quali si dispongono in modo tale da minimizzare gli effetti superficiali di demagnetizzazione. Questi domini sono separati da ‛pareti di Bloch' oltre le quali la magnetizzazione cambia da una direzione cristallografica di facile magnetizzazione a un'altra (v. fig. 16). Gli effetti di isteresi sono dovuti alla difficoltà di formazione di queste pareti o, più comunemente, agli ostacoli frapposti dai difetti del cristallo al loro spostamento.

Anche se la termodinamica che descrive l'ordine magnetico nel suo complesso è ben compresa, tuttavia è molto difficile predire i parametri di questa descrizione (valore dei momenti magnetici, accoppiamento tra di loro o con il reticolo): la struttura elettronica che sta alla base di questi fenomeni comincia appena ora ad essere compresa. Sono ancora mal compresi anche i dettagli delle fluttuazioni magnetiche, sia alle basse temperature, alle quali le onde di spin vengono quantizzate in ‛magnoni', sia vicino alla temperatura critica di ordine: la ‛temperatura di Curie' per i materiali ferro- e ferrimagnetici e la ‛temperatura di Néel' per quelli antiferromagnetici. Tuttavia, per quel che riguarda le fluttuazioni lente e a lungo raggio, che si hanno in prossimità della temperatura di Curie, sta emergendo un quadro abbastanza soddisfacente, specialmente quando gli accoppiamenti magnetocristallini sono sufficientemente deboli da far sì che le trasformazioni ferro-o ferrimagnetiche siano del secondo ordine.

6. Struttura elettronica dei difetti.

I difetti statici descritti in precedenza (v. cap. 4) hanno naturalmente speciali strutture elettroniche che sono responsabili delle loro proprietà.

1. Si è arrivati ora a comprendere le principali caratteristiche delle ‛superfici' o delle ‛interfacce' lisce, sia per i metalli sia per gli isolanti, e si è anche compreso, più o meno, l'ordine di grandezza delle proprietà fisiche che ne derivano: ad esempio, della tensione superficiale, della resistività o conduttività di superficie, dell'emissione termoionica e fotoionica dei contatti di raddrizzamento, ecc. Per avere dati attendibili si è dovuto aspettare il recente sviluppo delle tecniche di vuoto spinto, e soltanto ora si sta sviluppando un'analisi teorica particolareggiata. Problemi più complessi, invece, come quelli delle interfacce tra due fasi condensate, dell'adsorbimento di atomi o molecole, della catalisi, della corrosione, dell'emissione secondaria e dell'attrito, sono ancora in uno stadio preliminare.

2. Le grandi distorsioni atomiche al centro delle dislocazioni possono corrispondere alla rottura di legami nelle strutture covalenti oppure alla presenza di cariche non bilanciate nei solidi ionici; questi difetti rivestono sicuramente una certa importanza nei problemi inerenti ai fenomeni di trasporto nei semiconduttori o alla formazione di immagini latenti nelle reazioni fotografiche degli alogenuri di argento. Le distorsioni a lungo raggio sono responsabili dell'isteresi che si può indurre nei materiali magnetici con i procedimenti di indurimento: le dislocazioni ostacolano gli spostamenti delle pareti di Bloch tra i domini magnetici; effetti simili ostacolano anche il moto delle linee di vortice dei superconduttori. In ogni modo questi problemi di isteresi non possono essere risolti completamente se prima non si raggiunge una buona descrizione dei processi di indurimento.

3. Lo sforzo principale, in questo campo, si è concentrato, dalla guerra in poi, sullo studio dei difetti puntiformi.

La possibilità di unire insieme metalli per formare leghe non è una scoperta recente; tuttavia, nonostante che già sin da prima dell'ultima guerra mondiale si fosse ben compresa la legge che regola i diagrammi di fase delle leghe binarie, la natura esatta dell'interazione chimica tra gli atomi in soluzione è divenuta chiara solo di recente: essa spiega gli effetti di ordine e segregazione rispettivamente responsabili, ad esempio, della durezza del bronzo e del duralluminio.

La variazione della carica nucleare dovuta al difetto puntiforme produce un campo coulombiano che classicamente deve venir schermato dagli elettroni della matrice metallica. Lo schermaggio non è tuttavia perfetto: il principio di indeterminazione impedisce alla carica schermante di concentrarsi sul nucleo; l'ordine di grandezza della sua dispersione spaziale è dato dalla lunghezza d'onda λ_F degli elettroni di Fermi, cioè, normalmente, dalla distanza interatomica. I difetti puntiformi diffondono quindi gli elettroni di Fermi con una sezione d'urto effettiva dell'ordine delle dimensioni atomiche. Dal momento che la densità degli elettroni nella banda di conduzione si annulla quasi improvvisamente al di sopra del livello di Fermi E_F (v. fig. 7), l'effetto schermante e il potenziale di perturbazione dovuti al difetto puntiforme decrescono piuttosto lentamente all'aumentare della distanza e con oscillazioni di lunghezza d'onda dell'ordine di λ_F; da ciò sorgono piccole ma caratteristiche interazioni a breve raggio, attrattive o repulsive, tra i difetti puntiformi e l'ambiente circostante: spostamento di nuclei vicini della matrice che produce un effetto dimensionale, attrazione o repulsione di altri difetti puntiformi vicini.

Solo di recente inoltre si sono capite le peculiari proprietà elettriche e magnetiche di leghe come la costantana CuMn, le leghe di Heusley (ad es. Cu₂AlMn), le leghe invar (Ni CoFe) ecc. La loro comprensione è collegata con la descrizione degli orbitali d degli atomi di transizione, sia isolati in una normale matrice metallica, sia circondati da altri atomi di transizione con i quali possono formare bande d. In entrambi i casi, l'ibridizzazione degli stati sp della banda di conduzione è importante per le proprietà di trasporto; gli effetti di correlazione all'interno degli atomi possono dar luogo a momenti magnetici permanenti degli orbitali d. Infine, soltanto pochi anni fa, Kondo comprese che la diffusione degli elettroni di Fermi con ribaltamento dello spin doveva necessariamente distruggere i momenti magnetici delle impurità vicino allo zero assoluto: sembra che in effetti ci sia una transizione graduale tra impurità non magnetiche, con fiuttuazioni magnetiche eccitate termicamente, e impurità magnetiche a elevate temperature di Kondo.

Nel complesso, molte delle proprietà dei difetti puntiformi dei metalli possono venir predette con buona precisione facendo uso di modelli semplici ma efficienti. I metodi teorici sviluppati in questo campo sono stati usati successivamente nello studio della diffusione da parte di atomi degli elettroni di valenza nei metalli puri. Ci si può aspettare che ne segua un certo rinnovamento nella metallurgia fisica.

Sono tuttavia altri due i campi in cui la struttura elettronica dei difetti puntiformi è nota anche ai non specialisti: in primo luogo nei ‛semiconduttori', in cui quantità infinitesime di impurità modificano grandemente le proprietà elettriche, mutando il numero degli elettroni n eccitati nella banda di conduzione o delle lacune positive p eccitate nella banda di valenza. Lo studio sistematico di questi effetti ha dato popolarità ai metodi di purificazione spinta, come ad esempio quello della fusione a zone, dapprima usato per purificare i metalli.

Consideriamo un atomo sostitutivo vicino, nella tavola periodica, a quello della matrice entro cui si pone, ad esempio As in Ge. Lo ione tetravalente As⁺ prende facilmente il posto di un atomo di Ge formando quattro legami sp che sono polarizzati solo lievemente verso As. L'ultimo elettrone n dell'As neutro può trovar posto in uno degli stati vuoti nella banda di conduzione del Ge (v. fig. 14), ma può avere un'energia più bassa se viene catturato dal campo coulombiano dell'As⁺. La situazione è in qualche maniera simile a quella dell'atomo di idrogeno, se si esclude il fatto che l'elettrone non si muove nel vuoto, ma in un reticolo polarizzabile. Ne segue che le dimensioni dell'orbita sono dell'ordine di a = a₀ Km/m_c, dove K è la costante dielettrica del semiconduttore ed m_c la massa effettiva caratteristica delle onde di Bloch nella banda di conduzione: l'energia necessaria per ionizzare l'elettrone nella banda di conduzione diviene E_i ≃ (m_c/mK)R. Se è a₀ ≃ 0,5 Å, R = 13,5 eV, K ≃ 15 e m_c ≃ 0,2m, si hanno orbite con a ≃ 25 Å, molto più grandi cioè delle orbite atomiche, ed energie E_i ≃ 0,01 eV, molto minori delle distanze energetiche tra le bande. Gli elettroni di questi stati ‛donatori' vengono quindi termalizzati nella banda di conduzione a una temperatura molto inferiore rispetto a quella necessaria per eccitare efficientemente gli elettroni di valenza: perfino a concentrazioni molto basse queste impurità modificano profondamente le proprietà di trasporto a temperatura ambiente.

Se la valenza dell'atomo sostituito è più piccola di quella della matrice, come nel caso Ge-Ga, è il Ga^- che funge con facilità da sostituente. La neutralità viene mantenuta producendo una lacuna positiva p nella banda di valenza, la quale però risulta più stabile se viene catturata dal campo coulombiano del Ga^-. La situazione è simile a quella del caso precedentemente considerato, ma la ionizzazione della lacuna positiva corrisponde qui al trasferimento di un elettrone dalla sommità della banda di valenza a uno stato accettore di energia un po' più alta, con la creazione di una lacuna libera nella banda di valenza; anche i raggi delle orbite e le energie di ionizzazione sono simili. Se ora in una parte di un cristallo semiconduttore di tipo n si introduce un eccesso di impurità p, al bordo tra le due regioni si crea una giunzione pn con proprietà raddrizzanti analoghe a quelle di un diodo o di un contatto tra due differenti cristalli, con in più il vantaggio di una migliore riproducibilità e di un minore volume (v. fig. 17): vicino alla giunzione gli elettroni degli stati donatori n vengono trasferiti agli stati accettori p fintantoché il potenziale coulombiano di doppio strato U₀, che si forma, porta gli stati di lacuna della regione p a un livello di energia quasi eguale a quello degli stati elettronici nelle regioni n. Il potenziale di equilibrio U₀ è tale che la corrente j₁ dei portatori n, eccitati termicamente, che scorre da sinistra a destra attraverso la barriera, eguaglia la corrente j₂ dei portatori n riportati indietro da destra a sinistra dal campo elettrico nella giunzione: j₁ ≃ A exp(− U/kT), j₂ ≃ BU e j₁(U₀) = j₂(U₀). Se si applica un campo elettrico esterno ε, si ha U = U₀ − εL e la corrente prodotta diviene fortemente asimmetrica in ε:

j = j₁(U) − j₂(U) ≃ B{U₀(e^εL/kT − 1) + εL}.

Solamente per basse temperature, forti campi elettrici positivi e giunzioni sottili (diodi ‛Esaki', con grandi concentrazioni di impurità) si riesce ad apprezzare una corrente supplementare dovuta al trasporto per effetto tunnel dei portatori n negli stati p. Infine, mettendo insieme due giunzioni pn con opportuni contatti su un sandwich pnp, ad esempio, si ottiene un ‛transistore' che presenta le medesime proprietà amplificatrici di una valvola a triodo (v. elettronica). Esula dallo scopo di questo articolo la descrizione delle vaste ricerche, sia scientifiche sia tecnologiche, che sono state condotte in questo campo; va comunque notato che alcuni semiconduttori vengono usati in apparecchiature per la conversione dell'energia. Le proprietà delle batterie sono in effetti dovute alla formazione di taluni strati semiconduttori; il forte potere termoelettrico e la bassa conducibilità termica di alcuni semiconduttori sono stati usati per la conversione diretta di energia termica in energia elettrica e anche nella conversione diretta di luce in elettricità per effetto fotoelettrico si fa uso di questo tipo di conduttori.

Ricerche molto simili a quelle citate riguardano, da una parte, i solidi ionici più o meno isolanti, come ad esempio il CdS, usati per la loro ‛luminescenza', dall'altra i ‛maser' e i ‛laser' solidi, in cui gli elettroni legati alle impurità vengono eccitati dalla luce, più o meno allo stesso modo come negli atomi o nelle molecole gassose. In un laser a semiconduttore l'emissione di luce è dovuta alla ricombinazione diretta da banda a banda delle coppie elettrone-lacuna, iniettatevi attraverso una giunzione pn. Infine ricordiamo i ‛centri di colore' che sono difetti puntiformi, generalmente lacune o loro aggregati, che hanno catturato un portatore in uno stato localizzato. La mancanza di uno ione negativo produce localmente una scarsità di carica negativa, o un eccesso di carica positiva, che può catturare un elettrone; lo stato di impurità introdotto in questa maniera è in qualche modo simile a uno stato di donatore in un semiconduttore; tuttavia, le maggiori masse effettive e le costanti dielettriche più piccole portano a orbite di dimensioni atomiche e a energie di eccitazione e ionizzazione vicine allo spettro visibile: l'assorbimento della luce dovuto a questi ‛centri F' colora in maniera molto intensa i cristalli ionici. In maniera simile le lacune di ioni negativi possono catturare lacune positive e formare ‛centri V'; inoltre, ioni interstiziali positivi e negativi con diverso grado di ionizzazione si formano a seguito di danni da irraggiamento.

7. Conclusione.

Le basi della fisica dello stato condensato erano già solidamente poste, come si è detto, prima dell'ultima guerra, ma solo negli ultimi venti anni questa disciplina si è sviluppata in maniera notevole. Vi si possono riconoscere due direttive di ricerca: una più propriamente cristallografica che descrive le proprietà della materia in funzione dell'ordine atomico, l'altra più propriamente elettronica che si spinge più profondamente nello studio della struttura.

Per quanto necessario, il lavoro di base portato avanti sui cristalli perfetti è piuttosto noioso e ha dato di rado risultati spettacolari, se si eccettuano campi di avanguardia, come il magnetismo e la superconduttività. Ciò che ha dato il successo alle ricerche nel campo dello stato solido, a partire dalla guerra in poi, è stata la dimostrazione che le eccitazioni dei cristalli e i difetti statici del reticolo sono per lo meno altrettanto importanti quanto i cristalli stessi nello stato stabile, senza imperfezioni. La ‛patologia' dei cristalli e, più di recente, lo studio delle fasi amorfe si sono in effetti sviluppati come branche autonome, sufficientemente salde da polarizzare attualmente una buona parte dell'intero impegno della ricerca sullo stato solido. Questo impegno assume spesso un aspetto piuttosto tecnologico: probabilmente, però, ora si riesce a vedere più chiaramente la differenza di prospettiva e la considerevole mole di lavoro che distingue la ricerca di base, che elabora un linguaggio semplice ed efficiente per descrivere determinate classi di problemi fisici, dalla produzione di dispositivi o materiali effettivamente utili, affidabili e poco costosi.

In ultimo va ricordato che la fisica degli stati condensati della materia interessa altri campi, nei quali il linguaggio già elaborato può rivelarsi utile: si possono, ad esempio, ricordare i materiali biologici, in cui la stabilità, la simmetria e la riproducibilità di grossi insiemi ricordano le proprietà dei più elementari cristalli; la geologia e la geofisica pongono problemi riguardanti la stabilità, la reattività e la meccanica dei liquidi e dei solidi e le loro proprietà magnetiche, per la cui soluzione dovrebbe risultare utile la conoscenza degli stati condensati della materia, anche se in condizioni non estreme di temperatura e di pressione. Condizioni estreme si incontrano viceversa nelle stelle e in effetti la fisica delle stelle a neutroni pone problemi di fisica dello stato solido alla cui soluzione contribuiscono le conoscenze di recente acquisite sulla superconduttività, sulla conduzione termica e sulla plasticità.

Bibliografia.

Kittel, N. F., Introduction to solid state physics, New York 1971².

Mott, N. F., Jones, H., Metals and alloys, London 1936.

Seitz, F., Modern theory of solids, New York 1940.

Ziman, J., Electrons and phonons, London 1960.