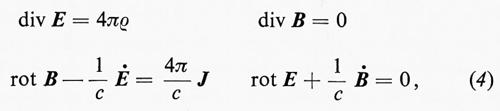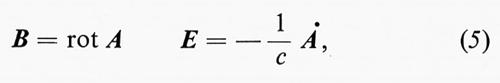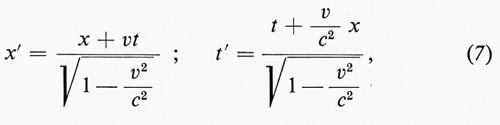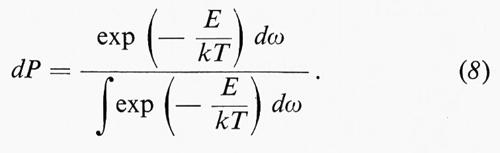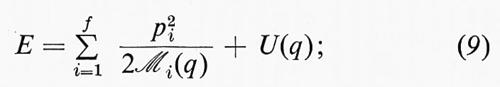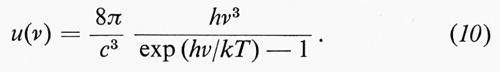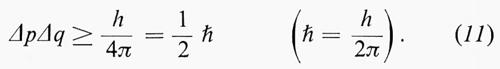Fisica

Fisica

di Bruno Ferretti

Fisica

sommario: 1. Introduzione. a) Obiettività secondo Poincaré. b) Storia naturale e fisica. c)  Il metodo sperimentale e il metodo teorico. d) Storicità della scienza. 2. Il tentativo classico verso l'unità dell'immagine fisica del mondo. a) Il tentativo meccanicistico. b) Il campo elettromagnetico; teoria della relatività; coronamento e inizio della crisi della fisica classica. c) La meccanica statistica. 3. La fisica del sec. XX. Fisica quantica. a) La prova della struttura atomica della materia e i paradossi che ne sorgon.  b) Il quanto d'azione. c) Dualità corpuscolare-ondulatoria. d) Fisica del nucleo; interazioni forti e deboli; fisica delle particelle elementari. 4. Questioni di metodo e di valore. a) Obiettività e arbitrarietà; errori di misura e indefinizione. b) Concetto di ‛obiettività classica' e principio di conplementarità. c) L'esperimento e la genesi delle teorie; il ‛dilemma del teorico'. d) Questioni di valore. □ Bibliografia.

1. Introduzione

a) Obiettività secondo Poincaré

Il mondo empirico si presenta come un continuum sui generis; dico sui generis perché non si tratta di continuità matematica, e nemmeno di una realizzazione di un continuo matematico (v., per es., Poincarè, 1903, p. 34).

Questo continuum presenta una estrema variabilità ed una estrema mutevolezza. Nonostante questo, noi pretendiamo di descriverlo con un linguaggio. Ciò non sarebbe possibile se, almeno in via approssimata, nel mondo empirico non fossero riconoscibili certe invarianze.

È compito della scienza naturale cercare di precisare e definire queste invarianze, e soprattutto di determinarne criticamente le connessioni strutturali e i limiti di applicabilità a una corretta descrizione dell'esperienza.

Vi è un tipo di invarianza generale che è comune a tutte le scienze naturali, e fa parte dei fondamenti della metodologia scientifica: è l'invarianza che, per esempio secondo Poincaré, serve a definire un certo concetto di obiettività. Ne riporterò la definizione con le parole stesse di Poincaré: ‟Quello che ci garantisce l'obiettività del mondo in cui viviamo è il fatto che questo mondo è comune ad altri esseri pensanti [...]. Questa è dunque la prima condizione dell'obiettività: ciò che è obiettivo dev'essere comune a diversi intelletti e, di conseguenza, si deve poterlo trasmettere dall'uno all'altro" (v. Poincarè, 1904, p. 212). In altre parole, ciò che è obiettivo è ciò che è invariante nella conoscenza dei diversi esseri umani. Una tale definizione comporta immediatamente che qualunque enunciato obiettivo deve essere controllabile: il suo valore di verità deve risultare in modo non ambiguo per il tramite di operazioni (logiche o empiriche) definite in modo da poter essere eseguite in via di principio da ogni essere umano, e con risultati indipendenti dal particolare individuo che le esegue.

b) Storia naturale e fisica

Naturalmente non è strettamente richiesto, nè d'altra parte nella maggior parte dei casi è possibile, che il controllo sia diretto; per esempio una delle fonti essenziali della conoscenza della natura è la conoscenza dei fatti o accadimenti naturali. Ora, ogni fatto, a stretto rigore, è essenzialmente irripetibile, quindi non può essere in se stesso direttamente controllabile dopo che è avvenuto.

Quando la conoscenza di singoli fatti, o di insiemi di fatti dati, è importante per sé, come accade nelle scienze aventi uno spiccato carattere storico (per esempio la paleontologia), sono controllabili e sottoposte a controllo obiettivo certe conseguenze o tracce lasciate dai fatti che direttamente interessano. Ciò del resto è vero non solo per la ‛storia naturale', ma anche per le scienze storiche propriamente dette.

Nel caso della fisica, non interessa in se stessa la conoscenza di singoli fatti, e questa è importante solo perché strumentale alla conoscenza di ‛invarianze naturali' le più generali possibili. Cerchiamo di spiegare mediante esempi cosa intendiamo con la locuzione, volutamente vaga, ‛le più generali possibili'.

Si consideri un sistema planetario costituito da una stella e da un solo pianeta. Le leggi della meccanica, la legge gravitazionale di Newton, che sono applicabili, per esempio, a tutti i sistemi planetari e in tal senso (in realtà in un senso molto più generale) sono invarianti, interessano la fisica. Interessa la fisica anche il fatto, deducibile dalle predette leggi, che (almeno nell'approssimazione in cui i due corpi in questione si possono considerare punti materiali sottratti a perturbazioni esterne) la velocità areale del moto planetario è invariante nel tempo. Quale sia il particolare valore di questo invariante, nel caso specifico, non è interessante in se stesso per la fisica; interessa invece l'astronomia; è infatti un dato che dipende dalla storia particolare di quel sistema planetario.

Ancora: gli specifici caratteri, relativamente invarianti, che definiscono una specie biologica, interessano la biologia. Le leggi della meccanica quantica, che rendono ragione della stabilità delle molecole proteiche e degli acidi nucleici - i quali costituiscono il fondamento materiale microscopico dell'invarianza delle specie biologiche (v. Monod, 1970; tr. it., p. 88) - interessano la fisica. Però le invarianze propriamente biologiche non sono riducibili meramente alla fisica; esse, se non altro, dipendono dalla storia particolare della vita, come essa è sorta e come si è evoluta sulla terra, storia che in se stessa esce dal campo della fisica.

Si potrebbe esser tentati di dire che in ogni fatto che si verifica in natura sono riconoscibili aspetti contingenti e determinazioni necessarie, e che la fisica cerca di astrarre dalla ‛contingenza' per dedicarsi allo studio della ‛pura necessità'. Questa distinzione tra contingenza e necessità non è però priva di ambiguità.

c) Il metodo sperimentale e il metodo teorico

L'idea stessa che esistono delle invarianze (leggi, regolarità, ecc.) di tipo estremamente generale, verificabili cioè nei più diversi ‛sistemi' (dai sistemi astronomici a quelli biologici) e nelle più diverse circostanze, suggerisce l'ipotesi che i complicati e variabilissimi fenomeni, i quali spontaneamente si presentano in natura, debbano essere analizzabili in termini di fenomeni essenzialmente più semplici, in cui le invarianze cercate si manifestino con sufficiente chiarezza. In particolare, poiché le leggi della fisica debbono essere invarianti per ‛traslazioni temporali' (ossia non debbono dipendere dall'origine dalla quale si comincia a misurare il tempo), questi ‛fenomeni semplici' debbono essere ‛riproducibili'.

Prescindendo dal caso di certi fenomeni astronomici, come i moti planetari, fenomeni che siano riproducibili con sufficiente approssimazione si ottengono, in generale, solo in circostanze artefatte.

Ecco perché la fisica è sorta veramente con la nascita del metodo sperimentale, secondo il quale il ricercatore, prima di accingersi ad ogni osservazione o misura, deve ‛creare' le circostanze in cui si produrranno i fenomeni che lo interessano, in modo tale che questi fenomeni siano, per quanto possibile, semplici, ‛puliti' e, come si è detto, riproducibili.

A questo scopo occorrono in generale misure, e misure precise. Infatti un enunciato relativo ad accadimenti naturali, che esprima risultati in forma numerica e con indicazione di limiti di errore, è in genere molto meno equivocabile, e quindi più facilmente obiettivo, di un enunciato che sia solo qualitativo. La ‛quantificazione' diventa poi indispensabile quando si debbano fissare in modo obiettivo le circostanze sperimentali in cui va eseguito un dato esperimento; quindi quasi sempre sono necessarie delle misure già quando si preparano le precise condizioni artefatte in cui debbono svolgersi i fenomeni che interessano.

La questione del ‛controllo' degli enunciati obiettivi in una scienza sperimentale diventa così particolarmente semplice, almeno in linea di principio, data la riproducibilità dei fenomeni interessati. Infatti, ogni controllo implica, in modo più o meno esplicito e chiaro a seconda dei casi, la verifica di una ‛predizione particolare'.

Affinché il controllo sia significativo, occorre che il verificarsi della predizione sia pure significativo. Ora, il verificarsi di una previsione quantitativa precisa è, ceterisparibus, molto più significativo del verificarsi di una predizione, sia pure anche quantitativa, ma poco precisa. Per esempio, è estremamente più facile indovinare con esattezza, del tutto casualmente, un numero di una cifra, che un numero di dieci cifre.

D'altra parte, la precisione in se stessa non basta a costituire alcun significato. È solo all'interno di un discorso che sia già, per sé, significativo, ossia all'interno di una teoria, che la precisione può diventare strumento discriminante tra fondamentali alternative, e quindi mutuare un significato talvolta di decisiva importanza obiettiva.

Non è una circostanza fortuita che il modo quantitativo di descrivere i fenomeni, connaturale al metodo sperimentale, sia anche connaturale all'uso del metodo matematico impiegato nello sviluppare le teorie della fisica.

Il metodo matematico permette innanzitutto di caratterizzare in modo logicamente preciso gli invarianti e le invarianze di cui abbiamo parlato fin qui in modo piuttosto vago.

Esistono quantità invarianti aventi un carattere universale, come, ad esempio, la velocità della luce nel vuoto, o l'esponente - 2 al quale è elevata la distanza e che è caratteristico della legge gravitazionale di Newton. Oppure, esistono quantità invarianti rispetto a certe operazioni di trasformazione, come, ad esempio, l'energia di un sistema isolato che è invariante per traslazione temporale. Esistono, inoltre, strutture logiche esprimibili mediante equazioni, come le equazioni di Maxwell, e invarianze di proprietà formali di certe strutture logiche, per certe trasformazioni, come ad esempio l'invarianza delle equazioni di Maxwell per le trasformazioni del gruppo di Poincaré.

Così il metodo matematico, tra l'altro, contribuisce in modo essenziale alla definizione dei concetti fisici tramite le loro correlazioni logiche chiaramente espresse nelle strutture matematiche in cui i concetti stessi sono nominati.

Tuttavia, non si deve pensare che il valore di una teoria fisico-matematica sia limitato al fatto che essa permette di formalizzare concetti e leggi meramente suggerite dalla esperienza.

Il valore massimo di una valida teoria consiste nella possibilità che essa fornisce di scoprire profonde e molto spesso del tutto insospettate relazioni tra differenti campi di esperienze, relazioni che permettono nuove controllabili predizioni e alle volte addirittura la scoperta di interi domini empirici di tipo totalmente diverso da quelli previamente conosciuti.

Così la teoria del campo elettromagnetico di Maxwell, includendo in una formulazione matematica precisa alcune geniali intuizioni di Faraday, ha permesso non solo di unificare l'ottica con l'elettromagnetismo, ma di predire, in via di principio in modo completo, e in via di fatto in molti dettagli, l'esistenza del totalmente nuovo e ricchissimo campo di esperienze costituito dalla fenomenologia delle onde hertziane, scoperte sperimentalmente in laboratorio solo vent'anni dopo la previsione teorica, e poi in natura, come onde radioastronomiche, parecchio tempo dopo.

Trionfi di questa importanza sono rari nella storia della scienza, e tuttavia sono quelli che meglio, più profondamente e chiaramente, ne qualificano gli scopi, la natura e il valore.

d) Storicità della scienza

Abbiamo detto che le teorie scientifiche rendono possibili la definizione dei concetti scientifici, l'espressione delle regolarità che si riscontrano in natura, sotto forma dileggi dinamiche o di altre strutture logiche, e infine la connessione di leggi e strutture particolari in strutture via via più ampie, generali e complete.

Si deve ora sottolineare il fatto importantissimo che concetti, strutture, metodi e risultati scientifici non hanno un carattere metastorico; nascono tutti, si mutano e si caratterizzano diversamente con il progresso stesso della scienza, in un processo che possiamo ben dire dialetticamente evolutivo.

In questo processo, non è tanto importante l'influenza storica dovuta a rapporti e interazioni della ricerca scientifica con le altre attività che si svolgono nella società umana, quanto una certa interna ragione evolutiva, intrinseca al formarsi della scienza, ragione che ne configura l'autonomia e che si deve tener presente e intendere anche se si è interessati in primo luogo a un solo momento di tale processo, ad esempio l'attuale. Il trascurarlo non può farsi senza esporsi al pericolo di una comprensione parziale, superficiale e distorta, anche del ristretto oggetto che può direttamente interessare.

Per questa ragione noi, che pure siamo principalmente interessati ad alcuni aspetti essenziali della problematica della fisica del secolo presente, troviamo indispensabile tratteggiare, prima di entrare in tale problematica, come essa si presentasse nel secolo passato.

V'è del resto un ‛invariante', che sembra dominare tutto lo sviluppo storico della scienza e fissarne ‛quasi metastoricamente' lo scopo ultimo: la ricerca della ‛unità dell'immagine fisica del mondo'. Scrive, per esempio, Planck (v., 1933; tr. it., p. 11): ‟La scienza della natura, fin dai suoi primordi, ha sempre avuto come ultimo e massimo scopo quello di riuscire a compendiare l'estremamente varia molteplicità dei fenomeni fisici in un sistema unitario, possibilmente in un'unica formula".

La ricerca di questa unità conferisce alla fisica la sua posizione singolare tra le scienze della natura: come abbiamo detto, la fisica si occupa delle invarianze naturali, le più generali.

Così facendo fornisce un potente strumento ‛esplicativo' alle altre scienze: una invarianza particolare che formi oggetto di studio di qualche scienza della natura che non sia la fisica, potrà essere considerata ‛completamente spiegata' quando sarà ridotta da una parte alle ‛leggi universali' della fisica, e dall'altra a un evento, o serie di eventi, di carattere contingente o storico, accaduti nel divenire della natura.

In tal modo la fisica fornisce anche un potente strumento di unificazione tra le diverse scienze della natura.

Questo potere unificatore della fisica era già stato supposto, più con lungimirante ardimento che con argomenti solidamente fondati, fin dal sorgere della scienza moderna, e questa ipotesi era stata corroborata, in modo significativo ma comunque non decisivo, dalle scoperte scientifiche del secolo passato.

Ma l'evidenza a favore di questa ipotesi generale della scienza è diventata esplosiva, per così dire, nel secolo presente, talché mai da quando la visione unitaria del mondo derivante dalla filosofia aristotelica era stata dimostrata illusoria, giustappunto dalle scoperte che hanno dato luogo al sorgere delle scienze moderne, si è stati così vicini all'ideale dell'‛unità dell'immagine fisica del mondo'. Questo risultato, penso, è uno dei maggiori titoli di autentica gloria non solo del pensiero scientifico, ma dell'intera problematica civiltà del sec. XX.

2. Il tentativo classico verso l'unità dell'immagine fisica del mondo

a) Il tentativo meccanicistico

È il tentativo che è stato più chiaramente e arditamente espresso per la prima volta nel modello generale del mondo secondo Laplace. Esso è stato suggerito dagli straordinari successi della meccanica celeste, dalla quale, d'altra parte, si originano o si precisano alcuni dei concetti e dei costrutti teorici fondamentali, quali quello di sistema fisico, di stato dinamico di un sistema, di massa, di quantità di moto, di momento angolare, di energia cinetica, di interazione, di energia potenziale e infine, soprattutto, di legge dinamica del moto. Questi concetti permangono, mutatis mutandis, nella meccanica relativistica e nella meccanica quantica, le quali hanno preso origine nel nostro secolo.

Per comprendere la ragione intrinseca del successo della meccanica celeste, è bene ricordare alcune cose, le quali, d'altra parte, costituiscono un esempio che si presta ad illustrare quella ‛ragione interna dell'evolversi della scienza', a cui accennavamo nell'introduzione.

Newton si fondò sulle leggi di Keplero e sulle idee di Galileo per ‛divinare insieme: a) il ‛concetto strutturale generale' di legge dinamica del moto; b) quali fossero in concreto queste leggi generali dinamiche del moto; e, infine, c) quale fosse la ‛legge della forza' agente tra gravi in funzione della massa e della distanza.

Ora, le leggi di Keplero sono leggi cinematiche di forma semplice ed elegante, che servono a descrivere il moto dei pianeti in una certa approssimazione.

Le leggi di Newton sono anch'esse di forma semplice ed elegante, ma di ben altra portata; la loro è una semplicità potente e sublime, ed esse posseggono una generalità che per secoli è sembrata veramente universale.

Le leggi di Keplero sono ben lungi dall'essere esatte; la loro approssimazione si deve considerare grossolana con gli standard odierni. Una descrizione meramente cinematica del moto dei pianeti, fatta con la precisione dei mezzi di osservazione e di misura odierni, conduce alla conclusione che questo moto è estremamente complicato, e nessuna semplicità apparente ne risulta all'infuori della semplicità profonda che è come nascosta nelle leggi dinamiche del moto; tale semplicità non sarebbe senz'altro estraibile, per così dire, dai dati di osservazione, se non si usassero giustappunto le leggi dinamiche stesse.

Naturalmente dalle leggi di Newton non si deducono, a rigore, le leggi di Keplero per il moto planetario, se non nel caso, estremamente schematico, di soli due punti materiali, gravitanti l'uno rispetto all'altro, e sottratti ad ogni altra interazione. Il moto che si deduce dalle leggi di Newton è quello effettivo, quale corrisponde alle più raffinate osservazioni possibili anche con la tecnica odierna - con l'unica eccezione del moto del perielio di Mercurio, di cui diremo poi - e anche per il caso più complicato e sofisticato del moto dei satelliti artificiali.

Le leggi di Newton risultano così dotate non solo di intrinseca semplicità e bellezza, fondata in modo ben più profondo della semplicità delle leggi di Keplero, ma di un potere di predizione che è senza precedenti.

Un esempio clamoroso e ben noto dell'efficacia di tale potere di predizione è offerto dalla scoperta del pianeta Nettuno, compiuta per merito di Adams e Leverrier nel 1846, dopo che la posizione di Nettuno era stata calcolata, in base alla teoria generale di Newton, come quella di un pianeta sconosciuto, responsabile di alcune irregolarità nell'orbita di Urano. In questo caso l'osservazione ha meramente confermato le predizioni fatte in base alla dinamica celeste. Un'analoga vicenda ha portato in questo secolo alla scoperta di Plutone, quindici anni dopo che la sua esistenza e la sua orbita erano state correttamente previste in base alla teoria.

Si può comprendere così come i fisici teorici cercassero di assumere il modello della meccanica celeste come modello onnicomprensivo nel tentativo di dare una ‛spiegazione fisica' o più modestamente una ‛descrizione fisica' unitaria di tutto il mondo.

Innanzitutto la validità illimitata, veramente universale, sia dei concetti generali della meccanica, sia delle leggi generali del moto, non era, dalla maggior parte dei fisici, nemmeno posta in discussione; ma, inoltre, a parte i ‛puristi' che volevano escludere dalla meccanica le ‛forze' e ridurre tutto ad urti tra particelle, i più mutuavano dalla meccanica celeste non solo i concetti e le leggi generali della dinamica, ma anche l'idea che tutti i sistemi fisici fossero costituiti da piccoli corpi o particelle, tra cui agissero forze di tipo centrale come nella meccanica celeste. Naturalmente non si supponeva che queste forze fossero tutte di tipo gravitazionale: una tale ipotesi sarebbe stata immediatamente contraddetta dall'esperienza. Ma la differenza fra la forza gravitazionale e queste ipotetiche forze centrali, agenti tra punti materiali o tra molecole, avrebbe dovuto essere espressa meramente da una differente legge di dipendenza dalla distanza.

Il compito del fisico teorico, una volta accettato uno schema di questo genere, era ridotto a quello di ricercare la forma di queste diverse leggi di forze centrali agenti fra le varie particelle costituenti il mondo, e poi di ricostruire, con il calcolo, i fenomeni quali appaiono all'osservazione.

Un tale programma, oltre che della fede nella meccanica e nelle forze centrali, si giovava chiaramente della rinascita dell'ipotesi atomica, la quale aveva cominciato ad imporsi con sempre maggiore vigore in seguito alle scoperte della chimica.

Tuttavia questo programma era troppo ambizioso e conteneva in sé una deficienza fatale (di cui avremo occasione di discutere); non aveva quindi alcuna possibilità di giungere al successo sperato.

Seguirono perciò abbastanza presto delusioni e uno scetticismo senz'altro eccessivo sulle possibilità della fisica teorica e in particolare della teoria atomica della materia.

Nonostante le sue limitazioni, il programma meccanicistico rese grandissimi servigi alla scienza, molto maggiori di quanto non pensassero i suoi critici. Per questa ragione ritengo opportuno ricordare, in modo un po' più tecnico di quanto non abbia fatto fino ad ora, alcuni concetti fondamentali della meccanica che ci saranno utili per il seguito.

Consideriamo, per fissare le idee, un sistema costituito da N punti materiali senza vincoli. Una configurazione del sistema sarà specificata in un istante t quando saranno assegnate le posizioni di tutti i punti costituenti il sistema rispetto a un dato riferimento. Questo potrà farsi assegnando 3N variabili indipendenti, per esempio le tre coordinate cartesiane ortogonali, rispetto a un sistema di assi rigidamente connesso con il riferimento, di ciascun punto costituente il sistema. Invece di un sistema di N punti materiali non vincolati, avremmo potuto considerare per esempio M corpi rigidi pure non vincolati: in tal caso, per specificare la configurazione del sistema sarebbero stati necessari 6M parametri indipendenti, ad esempio le coordinate dei baricentri degli M corpi e tre angoli euleriani per ciascuno dei corpi (per specificarne l'orientamento nello spazio).

In generale, si chiama ‛numero di gradi di libertà di un sistema' il numero dei parametri necessari e sufficienti per specificarne una configurazione.

Indicheremo in generale con f il numero di gradi di libertà; nel primo esempio f = 3N, nel secondo esempio f = 6M.

I parametri che, come funzioni del tempo, specificano istante per istante la configurazione del sistema si chiamano ‛coordinate lagrangiane'.

Negli esempi riportati fin qui, le coordinate lagrangiane hanno ovvi significati geometrici (e, come funzioni del tempo, cinematici) in relazione alla natura ‛corpuscolare' dei sistemi che si vogliono descrivere; ma è importante notare che una tale interpretazione geometrico-cinematica non è minimamente necessaria, e quando la si abbandoni, come avremo occasione di vedere, si può giungere ad una importante generalizzazione del concetto di sistema meccanico.

Qual è la forma generale delle leggi della meccanica, espresse mediante le coordinate lagrangiane? Questa forma generale può essere dedotta da un principio variazionale - il ‛principio di minima azione' - quando si faccia una speciale scelta del riferimento, che dovrà essere inerziale, e si introduca una funzione L delle coordinate lagrangiane q_i e delle loro derivate rispetto al tempo ó_i (i = 1, 2, ... f), funzione detta ‛lagrangiana' e che nel caso delle forze centrali, per esempio, si riduce alla differenza tra l'energia cinetica e l'energia potenziale. L'energia cinetica è una forma quadratica nelle ó, l'energia potenziale nel caso considerato non contiene le ó; le equazioni del moto (che si ottengono imponendo l'annullarsi della variazione dell'azione, cioè dell'integrale della lagrangiana lungo un arco di traiettoria possibile, ossia compatibile con le leggi del moto) si scrivono:

Le equazioni (1), che sono in numero f, si chiamano le equazioni di Lagrange del moto. Esse sono equazioni differenziali del secondo ordine nel tempo, e la loro soluzione è determinata quando, per esempio, siano assegnati i valori di tutte le q_i e di tutte le ó_i in un determinato istante. Per questo si dice che l'insieme dei valori delle q_i e delle ó_i a un dato istante specifica lo ‛stato dinamico' del sistema in quell'istante.

Come è ben noto dalla teoria dei sistemi di equazioni differenziali ordinarie, un sistema di f equazioni del secondo ordine può essere ridotto, e in infiniti modi, a un sistema di 2f equazioni del primo ordine. Nel caso delle equazioni di Lagrange, uno dei modi di effettuare questa riduzione, dovuto ad Hamilton, è particolarmente interessante. Per i sistemi meccanici semplici si riesce sempre facilmente ad applicare tale procedimento.

Hamilton introdusse le nuove variabili:

p_i = ∂L/∂ó_i, (2)

che vengono chiamate ‛variabili coniugate canonicamente delle q_i' ed esprimendo le derivate ó_i come funzioni delle p_k e delle q_k ricondusse le equazioni dinamiche del moto alla forma:

ó_i = ∂H/∂p_i; ñ_i = − ∂H/∂q_i, (3)

dove H è, nel caso che qui interessa, la somma dell'energia cinetica e dell'energia potenziale, ossia l'energia totale del sistema. H naturalmente deve essere espressa come funzione delle q_i e delle p_i e prende il nome di ‛hamiltoniana'.

Le equazioni (3) sono appunto 2f equazioni differenziali del primo ordine e prendono il nome di ‛equazioni canoniche della meccanica'.

Perché le equazioni canoniche sono particolarmente interessanti? Esse sono invarianti rispetto a un'ampia classe di trasformazioni che hanno il carattere delle cosiddette ‛trasformazioni di contatto'. Questa proprietà formale ha un profondo significato fisico, il quale può essere intuito ricordando che Hamilton giunse ai suoi risultati studiando le analogie formali che potevano sussistere tra il moto di corpuscoli e la propagazione di onde. All'epoca in cui Hamilton svolgeva le sue ricerche era ancora viva la disputa tra i sostenitori della teoria corpuscolare newtoniana della luce e quelli della teoria ondulatoria di Huygens. Le proprietà di ‛contatto' delle trasformazioni per le quali sono invarianti le equazioni canoniche ricevono un'interpretazione geometrica immediata nella costruzione di Huygens relativa al propagarsi delle onde.

È noto che già nella prima metà del secolo passato le esperienze sull'interferenza della luce, e altre sulla sua velocità di propagazione nei mezzi materiali, parvero decidere in modo definitivo la disputa sulla natura della luce a favore della teoria ondulatoria. Ma, come è ben noto, la questione risorse nel secolo presente, in forma del tutto inaspettata e apparentemente paradossale. Inoltre, le equazioni canoniche della meccanica si rivelarono preziose nella meccanica statistica. Questi due fatti (non incorrelati) spiegano, e lo vedremo meglio in seguito, come la forma canonica delle equazioni della meccanica abbia un'importanza fondamentale nella meccanica quantica.

Per questo abbiamo voluto ricordare le equazioni canoniche con un dettaglio maggiore di quello che riserveremo ad altri pur fondamentali argomenti della fisica.

Con il formalismo canonico, lo stato dinamico del sistema è specificato, nella meccanica classica, quando si assegnino insieme le coordinate lagrangiane q_i e i loro momenti coniugati p_i. Specificato lo stato dinamico del sistema isolato in un certo istante, esso risulta determinato anche in ogni istante passato o futuro rispetto a quell'istante.

Nella concezione di Laplace il mondo non è che un enorme sistema meccanico. Ogni fenomeno che accade nel mondo può essere espresso e descritto mediante assegnate funzioni delle coordinate lagrangiane e dei loro momenti coniugati, relativi a tutti i gradi di libertà del mondo stesso; quindi, una volta assegnato lo stato del mondo in un istante qualunque, tutti gli accadimenti naturali restano perfettamente determinati. Non vi è nulla di contingente o storico nel mondo di Laplace, se non lo stato dell'universo in un qualunque istante prefissato. Questa è l'espressione esatta del determinismo meccanicistico.

Un tale modello teorico ha esercitato ed esercita tuttora un enorme fascino su molte menti. Per molti rimane un ideale nella descrizione scientifica della natura. Discute- remo questa questione e le ragioni per le quali questo modello, lungi dall'essere l'unico razionalmente possibile, appare assolutamente non plausibile.

I teorici meccanicistici, per riuscire nel loro grandioso disegno, dovevano ridurre i fenomeni termici, quelli chimici e infine quelli elettromagnetici a fenomeni puramente meccanici. Esamineremo ora per sommi capi l'esito di questi tentativi.

b) Il campo elettromagnetico; teoria della relatività; coronamento e inizio della crisi della fisica classica

Inizieremo con il discutere i tentativi di interpretazione meccanicistica dell'elettromagnetismo. Tutta la teoria dell'elettromagnetismo è contenuta nelle equazioni di Maxwell:

nelle quali E indica il campo elettrico, B il campo magnetico, e la densità di carica elettrica, J la densità di corrente, e infine c è una costante universale uguale alla velocità della luce nel vuoto. Inoltre, alle (4) si può associare l'espressione della cosiddetta ‛forza di Lorentz', che dà la forza agente su una carica elettrica moventesi con una certa velocità in presenza di un dato campo elettrico e di un dato campo magnetico.

Ora, si possono scrivere le equazioni di Maxwell derivandole dal principio di minima azione applicato a un'opportuna lagrangiana e anche (nel caso più generale con qualche difficoltà che, tuttavia, è sormontabile) in forma canonica. La cosa può essere fatta molto semplicemente, per esempio, nel caso di un campo elettromagnetico, in assenza di cariche e correnti elettriche, contenuto in una cavità di volume finito e le cui pareti riflettano perfettamente le onde elettromagnetiche, introducendo le relazioni:

dove A è il cosiddetto ‛potenziale vettore', al quale imponiamo la condizione div Α = 0.

Si può allora facilmente mostrare che il campo elettromagnetico all'interno della cavità è descrivibile tramite la sovrapposizione di un'infinità numerabile di campi, ciascuno vibrante secondo un modo proprio della cavità. A ciascun modo, sia per esempio il modo n, corrisponde un'ampiezza A_n della vibrazione del potenziale vettore relativo a quel modo. Gli A_n possono pensarsi funzioni del tempo e possono assumersi come coordinate lagrangiane del sistema. L'equazione del moto per ciascuna coordinata A_n è allora quella di un oscillatore armonico di frequenza ben determinata dipendente dall'indice n. È chiaro che tale equazione del moto può mettersi in forma canonica e così l'intero ‛sistema del campo elettromagnetico' nella cavità diventa equivalente a un sistema meccanico avente un numero infinito di gradi di libertà e precisamente a un insieme di infiniti oscillatori armonici di frequenze ben determinate ma tutti indipendenti gli uni dagli altri. È allora immediato scrivere le equazioni canoniche del moto dell'intero sistema.

È però ben chiaro che nel caso presente le coordinate lagrangiane A_n hanno perso qualunque significato cinematico riferentesi a particelle; gli oscillatori di cui si parla non sono oscillatori materiali.

Per questa ragione la riduzione delle equazioni dell'elettromagnetismo alla forma canonica della meccanica non è sufficiente per affermare che l'elettromagnetismo sia ridotto a un fenomeno meccanico nel senso stretto in cui lo intendevano i meccanicisti.

Per ciò doveva essere possibile esprimere per esempio le quantità A_n come funzioni delle coordinate di ipotetiche particelle e far vedere poi che le equazioni di Maxwell potevano essere ricondotte alle equazioni del moto di queste particelle. Questo era esattamente il problema della riduzione in senso stretto dell'elettromagnetismo alla meccanica. Molti sforzi furono dedicati alla soluzione di questo problema da parte dei fisici teorici nella seconda metà del secolo passato. Ma la stessa sensatezza del problema fu messa in dubbio dalla scoperta di un celebre teorema di Poincaré (v., 1901). Per comprendere la portata del teorema occorre dire che le grandezze fisiche direttamente accessibili all'esperienza sono i campi E e B; le coordinate lagrangiane delle ipotetiche particelle materiali (sia pure di una materia sui generis, giacché esse erano pensate come le molecole costituenti l'ipotetico ‛etere cosmico') erano considerate viceversa come ‛variabili nascoste', cioè non direttamente accessibili all'esperienza. Ora, il teorema di Poincaré mostra che, se esiste una soluzione del problema meccanicistico dell'elettromagnetismo, allora ne esistono infinite non equivalenti. Queste infinite diverse soluzioni non comportano d'altra parte alcuna diversa predizione sperimentalmente verificabile; le variabili propriamente meccaniche sarebbero nascoste e apparentemente destinate a restare tali per sempre. Fin da allora si cominciò a dubitare molto seriamente che a tali grandezze si potesse assegnare un qualsiasi significato fisico e similmente si potesse assegnare un significato fisico a una descrizione strettamente meccanicistica dell'elettromagnetismo.

Ma il colpo praticamente definitivo contro una tale possibilità venne dalla scoperta della teoria della relatività.

Le equazioni della meccanica classica sono invarianti rispetto alle trasformazioni cinematiche di Galileo (relative a due sistemi di riferimento inerziali in moto rettilineo e uniforme l'uno rispetto all'altro):

x′ = x + vt; t′ = t, (6)

dove v è la velocità costante di traslazione parallela all'asse x.

In ciò consiste il principio di relatività classica. Le equazioni di Maxwell (4) non sono invarianti per le trasformazioni (6). In esse figura la velocità c e non vi è velocità invariante per trasformazioni di Galileo.

Secondo la fisica classica, le (4) dovevano valere pertanto solo in un determinato riferimento che naturalmente, secondo l'interpretazione meccanicistica, doveva essere il riferimento di quiete dell'etere cosmico.

Ma ogni tentativo di rivelare, mediante lo studio di opportuni fenomeni elettromagnetici, un moto rispetto al supposto etere cosmico, che sarebbe stato in certo senso un moto assoluto, regolarmente fallì.

Ciò portò Einstein a formulare l'ipotesi che tutti questi fallimenti non fossero casuali, ma fossero dovuti all'esistenza di un principio generale - ‛principio di relatività ristretta einsteiniana' - secondo il quale le equazioni di Maxwell rimangono invarianti per la trasformazione che fa passare da un sistema di riferimento inerziale a un altro in moto rispetto al primo. Pertanto Einstein suppose che le trasformazioni spazio-temporali subordinate a tale passaggio non fossero le (6) di Galileo, ma le trasformazioni di Lorentz:

per le quali le equazioni di Maxwell e la velocità della luce sono invarianti (v. relatività). Naturalmente quest'ipotesi può essere consistente con la possibilità di una descrizione unitaria del mondo fisico solo se si postula che anche le leggi della meccanica siano invarianti per le trasformazioni di Lorentz; a questo scopo non è necessario cambiare la forma generale delle equazioni canoniche della meccanica; basta modificare opportunamente l'espressione della funzione hamiltoniana H.

Tutte le conseguenze della relatività ristretta einsteiniana, sia nell'elettromagnetismo, sia nella meccanica, sia nella cinematica (la quale ultima nella teoria della relatività presenta gli aspetti a prima vista più paradossali per il cosiddetto senso comune), sono state confermate dall'esperienza e queste conferme sono state numerosissime e di diversa specie.

Si suole dire che la teoria della relatività einsteiniana per le nuove concezioni che introduce sullo spazio e sul tempo segna la fine della fisica classica e l'inizio della fisica moderna. Io direi piuttosto che segna il coronamento della fisica classica, giacché essa semplicemente estende al campo elettromagnetico il principio di relatività della meccanica classica. Sotto un aspetto però la relatività ristretta einsteiniana è veramente rivoluzionaria nei riguardi delle concezioni classiche e questo aspetto ci interessa particolarmente: l'idea di ‛etere cosmico' è svuotata di ogni contenuto fisico. Nella fisica classica, prescindendo anche da ogni tentativo di stretta interpretazione meccanicistica del campo elettromagnetico, il campo stesso era interpretato come una ‛proprietà' della ‛sostanza' etere cosmico. Ora è rimasto il campo ma è scomparso l'etere (come il sorriso del gatto del Cheshire che continuava a permanere anche quando spariva il gatto). In questo modo in realtà veniva messo in crisi l'uso acritico di uno dei concetti fondamentali che la scienza classica aveva ereditato in blocco dalla metafisica aristotelica: il concetto di ‛sostanza'.

Prima di abbandonare questo argomento vorrei ricordare la generalizzazione data da Finstein della propria teoria della relatività. Secondo la relatività ristretta, come abbiamo detto, le leggi della fisica devono essere invarianti per la trasformazione cinematica che fa passare da un sistema di riferimento inerziale a un altro, pure inerziale, cioè in moto traslazionale uniforme rispetto al primo. Nella sua relatività generale, Einstein ha cercato di esprimere le leggi della fisica in modo invariante rispetto a trasformazioni di tipo generale, cercando di eliminare così il carattere privilegiato dei sistemi di riferimento inerziali.

In tal modo, basandosi sul fatto sperimentale dell'equivalenza tra la massa inerziale e quella gravitazionale, è giunto a dare una teoria di campo della gravitazione. Come nella teoria del campo elettromagnetico, quando si passa da un sistema inerziale in cui per esempio c'è solo un campo magnetico e il campo elettrico è nullo a un altro in moto rispetto al primo, si ‛crea' nel secondo sistema un campo elettrico diverso da zero, così nella teoria della relatività generale, passando da un sistema di riferimento in cui il campo gravitazionale è nullo ad un altro in moto accelerato rispetto al primo, si ‛crea' un campo gravitazionale.

Con grande profondità di pensiero, la teoria della relatività generale connette le proprietà metriche dello spazio- tempo con la ‛presenza' della materia-energia nell'universo. Non entreremo in ulteriori dettagli su questa teoria (per la quale rimandiamo all'articolo relatività). Diremo soltanto che, mentre la relatività ristretta ha avuto, come già accennato, gran copia di conseguenze confermate dall'esperienza, poche sono le conseguenze della relatività generale direttamente verificabili dall'esperienza con le tecniche attuali. Ne menzioneremo solo due: la prima è la corretta previsione del movimento del perielio di Mercurio che costituiva l'unico mistero lasciato insoluto dalla teoria newtoniana nella descrizione dei moti planetari. La seconda è la previsione che la luce debba subire l'azione del campo gravitazionale in ragione delle due leggi di equivalenza della massa-energia, dedotta già nell'ambito della relatività ristretta, e della massa inerziale-massa gravitazionale, fondamento della relatività generale.

c) La meccanica statistica

Secondo il nostro programma, dobbiamo ora discutere il tentativo classico di ridurre i fenomeni termici e quelli chimici a fenomeni puramente meccanici. Questo tentativo è naturalmente basato sulla teoria atomica della materia, ed è stato realmente determinante, come vedremo, per i grandi progressi della fisica del secolo presente. Ciò è innanzitutto dovuto alla creazione della meccanica statistica, necessaria se si vogliono interpretare le proprietà fisiche macroscopiche dei corpi, e in particolare quelle termiche, sul fondamento della teoria atomica.

Era già chiaro infatti, fino dall'antichità, che gli atomi, se realmente fossero esistiti, avrebbero dovuto essere molto piccoli rispetto ai corpi che cadono sotto l'osservazione diretta dei sensi, cioè rispetto ai corpi macroscopici. Ciò comporta il fatto che il numero degli atomi eventualmente contenuti in qualunque corpo macroscopico deve essere estremamente elevato, e quindi che un corpo macroscopico, se pur può essere considerato come un mero sistema meccanico, deve essere necessariamente un sistema meccanico con un enorme numero di gradi di libertà. È perciò impossibile una descrizione completa ed esatta del moto interno di questo sistema meccanico, nonché risolvere le equazioni del moto. Infatti sarebbe impossibile assegnare il preciso stato dinamico iniziale del sistema costituito da un corpo macroscopico comunque piccolo. Fortunatamente, ciò non è neppure necessario, poiché a noi basterebbe poter specificare il comportamento macroscopico dei corpi (ad esempio, la legge che dà la pressione di un gas in funzione della sua temperatura e del suo volume) a partire dalla forma generale delle leggi dinamiche del moto che noi ben conosciamo, e, tutt'al più, dalla specificazione delle leggi delle forze di interazione tra gli atomi. Ora, ciò diviene possibile se le leggi macroscopiche che ci interessano sono proprietà di opportune medie sugli stati dinamici microscopici del sistema, e questo è precisamente il caso. Naturalmente, però, a stretto rigore, leggi dinamiche e leggi di forza non saranno del tutto sufficienti; dovremo in un modo o in un altro introdurre delle ipotesi di tipo probabilistico, allo scopo di dare un senso preciso alle proprietà medie che ci interessano. Queste ipotesi probabilistiche dovranno essere consistenti con le leggi del moto, da una parte, e servire poi effettivamente a descrivere l'apparente semplicità del comportamento macroscopico dei corpi (quale espressa per esempio dalle classiche leggi della termologia) in termini di medie sui complicatissimi movimenti microscopici dei costituenti elementari dei corpi stessi.

Nacque così nel secolo passato, principalmente per merito di Maxwell e di Boltzmann, una nuova disciplina, la meccanica statistica, che appunto doveva almeno parzialmente rispondere ai problemi posti nel programma or ora delineato (v. meccanica statistica).

Nella teorizzazione della meccanica statistica risulta particolarmente preziosa, come abbiamo già detto, la formulazione canonica delle leggi della dinamica.

Nella meccanica statistica è molto conveniente far uso del cosiddetto ‛spazio delle fasi'. Lo spazio delle fasi, per un sistema con f gradi di libertà, ha 2f dimensioni e un suo punto generico ha come coordinate cartesiane ortogonali le q_i e le p_i (variabili canoniche del sistema).

Se per esempio le condizioni esterne imposte al sistema sono tali che esso è confinato entro un volume finito V dello spazio ordinario e se, inoltre, l'energia del sistema è in qualche modo limitata - ciò che accade, per esempio, se si impone direttamente che essa sia compresa tra il valore E e il valore E + ΔE - allora il volume dello spazio delle fasi che può essere disponibile per il punto P, rappresentante lo stato dinamico del sistema, è anch'esso limitato. Se si considera ora un grande insieme di sistemi tutti uguali che siano ciascuno all'equilibrio termodinamico e tutti con un'energia compresa tra E ed E + ΔE, con ΔE infinitesimo, si dice che la distribuzione dei punti che rappresentano i loro stati dinamici microscopici nello spazio delle fasi è ‛microcanonica'.

Tutta la meccanica statistica può essere agevolmente dedotta dall'ipotesi che in una distribuzione microcanonica i punti rappresentativi siano uniformemente distribuiti nella porzione di spazio delle fasi accessibile a ciascun sistema.

Noi non potremo, per ragioni di brevità, far cenno ai numerosi e importanti lavori teorici fatti per saggiare la consistenza di questa ipotesi statistica con le leggi della dinamica (ricerche sui teoremi ergodici e quasi ergodici, le quali hanno avuto importanti sviluppi proprio nel secolo presente; v., per es., Khinchin, 1949). Diremo solo che l'ipotesi si può considerare pienamente giustificata dalla verifica delle sue conseguenze, alcune delle quali assai dirette e controllate positivamente da numerosi risultati sperimentali.

Per la meccanica e la termodinamica statistica ha una grande importanza la nozione di ‛distribuzione canonica', cioè la distribuzione dei punti rappresentativi degli stati di un grandissimo numero di sistemi identici, ciascuno, per esempio, con f gradi di libertà e ciascuno in equilibrio termico con un bagno di calore alla stessa temperatura T. Il bagno di calore è concepito come un sistema meccanico avente un grandissimo numero di gradi di libertà, in tutti i casi estremamente maggiore di f.

La distribuzione dei punti rappresentativi nello spazio delle fasi dei sistemi a f gradi di libertà nel caso canonico è deducibile dall'ipotesi statistica fatta sulle distribuzioni microcanoniche ed è espressa tramite la legge canonica di Boltzmann:

In tale legge dP rappresenta la probabilità di trovare il punto rappresentativo del sistema entro l'elemento di volume dello spazio delle fasi dω = Πf_idq_idp_i, E è l'energia che ha il sistema quando il suo punto rappresentativo si trova nell'elemento dω dello spazio delle fasi, T è la temperatura e k è una costante universale detta costante di Boltzmann.

Nei sistemi meccanici che noi consideriamo (forze centrali), con una scelta opportuna delle coordinate lagrangiane q_i, è sempre possibile esprimere l'energia nella forma:

ℳ_i(q), U(q) sono funzioni solo delle q_i; U(q) è l'energia potenziale. Il termine p²_i/2ℳ_i(q) può essere evidentemente interpretato come energia cinetica dell'i-esimo grado di libertà.

Si deduce dalla legge di Boltzmann che il valor medio dell'energia cinetica di ciascun grado di libertà è indipendente dal grado di libertà stesso, ed è precisamente uguale a kT/2; è questo il celebre teorema dell'equipartizione dell'energia cinetica, il quale, come vedremo, è, in certe condizioni, verificabile direttamente dall'esperienza e come tale è uno dei fondamenti della prova raggiunta in questo secolo della cosiddetta realtà dell'esistenza degli atomi.

Occorre dire a questo punto che, finché per merito di Perrin questa prova non fu raggiunta, per diverse ragioni, in parte dovute al fallimento delle teorie meccanicistiche dell'elettromagnetismo, in parte per difficoltà interne alla meccanica statistica stessa, i fisici e i chimici erano molto scettici sulla ‛realtà degli atomi' e perfino sulla sensatezza di porsi la questione se gli atomi fossero reali o no. Questo scetticismo, senz'altro eccessivo, era però prevalente alla fine del secolo passato e nei primissimi anni di quello presente.

Infine, vorrei citare, sia per la sua importanza concettuale, sia perché avremo occasione di riparlarne, una delle difficoltà in cui incorreva la meccanica statistica: il cosiddetto ‛paradosso di Loschmidt', che è il seguente: com'è possibile che le leggi della meccanica, le quali sono invarianti se si cambia il verso del tempo, almeno nel caso delle forze centrali, e quindi non possono descrivere direttamente che fenomeni reversibili, possano poi viceversa render conto dell'essenziale irreversibilità dei fenomeni macroscopici?

Questa questione, come altre interessanti per esempio la chimica, che erano però meno acutamente percepite, trovano la loro risposta più soddisfacente nel quadro della meccanica quantica come vedremo in seguito.

3. La fisica del sec. XX. Fisica quantica

a) La prova della struttura atomica della materia e i paradossi che ne sorgono

Secondo la concezione classica, condizioni necessarie e sufficienti perché un corpo macroscopico abbia realmente una struttura atomica sono le seguenti: a) il suo numero di gradi di libertà sia finito; b) sia possibile interpretare ciascuno di questi gradi di libertà come coordinata cinematica di una particella.

Il teorema dell'equipartizione dell'energia cinetica ci dà in linea di principio la possibilità di controllare sperimentalmente se la prima delle condizioni su esposte è soddisfatta e di determinare anche, almeno in alcuni casi, qual è il numero effettivo di gradi di libertà di un corpo macroscopico. Infatti, secondo il principio dell'equipartizione dell'energia, a ogni grado di libertà deve competere all'equilibrio termico la stessa energia cinetica. Poiché l'energia interna di un corpo macroscopico finito è necessariamente finita, segue che, se il numero di gradi di libertà del corpo fosse infinito, a ciascun grado di libertà all'equilibrio termodinamico dovrebbe competere un'energia cinetica nulla. Se dall'esperienza tale energia cinetica risulterà diversa da zero (e se naturalmente si crede al principio dell'equipartizione dell'energia), si dovrà necessariamente concludere che il numero di gradi di libertà del corpo è finito.

In questo modo si sarà dimostrato che la prima essenziale e caratterizzante condizione per concludere che la materia ha una struttura atomica è verificata dall'esperienza.

Questa è la linea di pensiero che ha guidato le celebri ricerche di Perrin sul moto browniano e che permette di comprenderne la fondamentale importanza.

Il moto di Brown, che può essere osservato facilmente su particelle molto minute visibili anche a un normale microscopio ottico a forte ingrandimento, era noto da un pezzo, ma era stato interpretato come dovuto a correnti di convezione del fluido in cui le particelle sono immerse, provocate da piccole accidentali differenze di temperatura; in altre parole, si era pensato che questo movimento fosse dovuto al fatto che il sistema che veniva osservato (fluido+particelle immerse) non fosse in equilibrio termodinamico.

Ora Perrin dimostrò, con una imponente serie di misure estremamente accurate, in condizioni controllatissime, che il moto browniano continua immutato anche quando il sistema si approssimi quanto si vuole all'ideale equilibrio termodinamico. Si tratta di un fenomeno che non è quindi interpretabile sul fondamento della termodinamica classica (non statistica), ma che rivela un fatto fondamentale genuino: anche all'equilibrio termodinamico l'energia cinetica relativa a un grado di libertà traslazionale di una particella continua ad essere diversa da zero. Questo è quanto precisamente è previsto dalla meccanica statistica nel caso in cui il sistema abbia un numero finito di gradi di libertà. Risulta anzi così possibile giungere a una determinazione più o meno diretta (con i metodi moderni molto diretta) del valore che ha l'energia cinetica media relativa a un grado di libertà, del valore della costante di Boltzmann (k = 1,380•10^-16 erg/°C) e quindi del numero di gradi di libertà di un corpo macroscopico.

Ora la forza della prova raggiunta inizialmente con lo studio del moto browniano diventa veramente conclusiva per il fatto che la costante di Boltzmann, o equivalentemente il numero di Avogadro, può essere determinata per altre vie, alcune estremamente dirette, come la determinazione della carica elettrica elementare (e = 4,802•10^-10 unità elettrostatiche) tramite l'esperienza di Millikan. Tutte queste determinazioni danno risultati concordanti entro gli errori con quello dato dalle esperienze di Perrin.

Si comprende come, in tal maniera, si sia giunti non solo a confermare i risultati ottenuti con lo studio del moto browniano, ma a dimostrare che, in certo senso almeno, gli atomi esistono e sono i costituenti dei corpi che cadono sotto la nostra esperienza diretta.

La prova fondata sul moto browniano assume però implicitamente che gli atomi, e talvolta le molecole, non abbiano gradi di libertà interni. Questo porta immediatamente a un grave paradosso. Infatti, prima ancora che Perrin compisse le sue esperienze, e i fisici ne fossero persuasi, numerosi fenomeni avevano convinto i ricercatori che prendevano sul serio la teoria atomica che se gli atomi esistevano dovevano avere una struttura interna e quindi gradi di libertà interni. Questi fenomeni erano essenzialmente relativi all'interazione tra la radiazione elettromagnetica e la materia. Innanzitutto gli spettroscopisti avevano già dimostrato da un pezzo che esistono spettri caratteristici degli elementi e quindi che, secondo la teoria atomica, si dovevano considerare caratteristici degli atomi. Inoltre, nel 1895, seguendo le indicazioni di una teoria di Lorentz sull'emissione da parte della materia di radiazioni elettromagnetiche, Zeeman aveva mostrato che un campo magnetico modifica lo spettro emesso per esempio dagli atomi, producendo caratteristiche separazioni delle righe atomiche, in alcuni casi almeno, in pieno accordo con quanto Lorentz aveva previsto (effetto Zeeman normale). Nella teoria di Lorentz le cariche elettriche che danno luogo alla densità che figura al secondo membro della prima delle equazioni (4) sono cariche possedute da particelle, i cosiddetti elettroni, e così le correnti sono dovute al moto degli elettroni. Gli elettroni si muovono secondo le leggi della meccanica classica sotto l'azione delle forze di Lorentz. Secondo la teoria, nell'espressione della separazione delle righe provenienti dalla scissione della stessa riga per effetto Zeeman, compare, oltre al campo magnetico, solo il rapporto e/m tra la carica elettrica e la massa degli elettroni.

L'anno dopo l'esperienza di Zeeman, Thomson trovò lo stesso valore per e/m studiando invece la natura dei raggi catodici. Naturalmente nulla poteva dirsi di sicuro finché non fosse stato noto almeno il valore di e, ma, come abbiamo ricordato, l'esperienza di Millikan prova direttamente l'atomicità dell'elettricità e determina il valore di e in modo univoco. Anche il valore di m può quindi essere determinato, e risulta, nel caso delle particelle dell'effetto Zeeman e dei raggi catodici, quasi duemila volte più piccolo di quello della massa dell'atomo di idrogeno (v. atomo).

Da tutti i fatti sopra riferiti, appare quasi inevitabile una conseguenza: gli elettroni sono componenti degli atomi. Questa conseguenza è confermata da infiniti altri fatti, primo tra i quali che gli atomi possono giust'appunto essere ionizzati strappando loro elettroni, mediante un'energia migliaia di volte inferiore all'energia di riposo dell'elettrone.

Ma se le cose stanno così, come abbiamo detto, gli atomi non sono in realtà atomi, ma hanno una struttura interna, quindi gradi di libertà interni. La questione è: come mai tali gradi di libertà interni non si fanno sentire a norma del principio di equipartizione dell'energia?

Il problema diventa particolarmente acuto se si entra nei dettagli della struttura atomica, come successivamente si è potuto fare per merito dei fondamentali lavori di Rutherford.

In molti casi gli atomi sono neutri. Se tali atomi contengono degli elettroni, che sono carichi negativamente, debbono contenere anche una carica positiva; Rutherford (1906), inaugurando un metodo che è rimasto a tutt'oggi il principale nello studio di strutture atomiche, nucleari e delle cosiddette particelle elementari, pensò di risolvere il problema della distribuzione della carica positiva all'interno dell'atomo, bombardando l'atomo stesso con opportuni proiettili. Usò come proiettili le particelle α, ne studiò la diffusione elastica e giunse all'importantissima conclusione che la carica elettrica positiva è concentrata, insieme alla quasi totalità della massa atomica, in una zona pressoché puntiforme rispetto alle dimensioni atomiche.

Appoggiandosi quindi a ben solide basi sperimentali, Rutherford fu in grado di formulare il suo celebre modello di atomo, in cui gli elettroni gravitano come minuscoli pianeti attratti da una forza centrale inversamente proporzionale al quadrato della distanza, come nel caso newtoniano.

Ma, per il cosiddetto teorema del viriale della meccanica statistica, l'energia cinetica media in un sistema di tipo newtoniano è pari alla metà, cambiata di segno, dell'energia potenziale media. Applicando questo teorema è facile vedere che un insieme di sistemi di tipo newtoniano ha calore specifico negativo. Come conseguenza, se è in grado di irraggiare energia elettromagnetica, come nel caso che ci interessa, esso continuerà a irraggiare indefinitamente, mentre la sua temperatura andrà continuamente aumentando. In altre parole, l'atomo di Rutherford è catastroficamente instabile.

Altre difficoltà relative ai calori specifici si venivano rivelando: nel caso dei gas, particolarmente per le molecole poliatomiche, e nel caso dei solidi, per i calori specifici a temperature molto basse. Un solido può essere schematizzato, molto grossolanamente, come un insieme di atomi oscillanti attorno a posizioni di equilibrio determinate dal suo reticolo cristallino. Se le oscillazioni non sono molto ampie, esse potranno essere considerate, sempre in un'approssimazione molto grossolana, come oscillazioni indipendenti ed armoniche. Un solido contenente n atomi è allora equivalente a un sistema di n oscillatori armonici. Per inciso, osserviamo che in questo caso, e con questo modello, gli oscillatori in gioco sono dei sistemi materiali. Ora, in un oscillatore armonico, l'energia cinetica media è uguale all'energia potenziale media. Pensando un atomo come un punto materiale, esso ha tre gradi di libertà, per cui all'equilibrio termodinamico la sua energia media è 3kT. Ne segue immediatamente la legge di Dulong e Petit. Questa legge va abbastanza bene, a temperatura ordinaria, per la maggior parte dei solidi; ma, quando si abbassa la temperatura, si trova che il calore specifico diminuisce per tutti i solidi, tendendo a zero quando la temperatura tende allo zero assoluto. Questo è ancora un fatto che sembra in patente contraddizione col principio classico dell'equipartizione dell'energia.

Se abbandoniamo per un momento la materia e passiamo a considerare la radiazione in equilibrio termodinamico all'interno di una cavità chiusa, troviamo un altro fatto catastrofico: questa volta la capacità termica di una cavità chiusa, pur in assenza di qualunque materia all'interno della cavità, appare essere infinita per il fatto che la cavità può contenere radiazione elettromagnetica. Ciò si può intendere facilmente, se ricordiamo che la radiazione elettromagnetica all'interno di una cavità chiusa, come abbiamo detto, è equivalente a un insieme di oscillatori. Ma questa volta si tratta di un insieme di infiniti oscillatori e quindi, poiché a ciascun oscillatore, all'equilibrio termodinamico, dovrebbe competere l'energia media kT, l'energia totale contenuta nella cavità dovrebbe essere infinita. Inoltre, semplicemente contando i modi di vibrazione della cavità in funzione della frequenza, si trova che quest'energia dovrebbe indefinitamente crescere verso l'ultravioletto estremo, in patente contraddizione con l'esperienza.

Tutti questi fatti hanno qualcosa in comune: non si può negare ogni validità al principio di equipartizione dell'energia, perché esso è confermato direttamente dalle esperienze di Perrin; ma, d'altra parte, tutto va come se, in certe circostanze, certi gradi di libertà fossero totalmente, o almeno parzialmente, ‛congelati'. Ma precisamente in quali circostanze, quali gradi di libertà, come e perché?

b) Il quanto d'azione

Il bandolo della matassa era già stato trovato da Planck (1900), prima delle ricerche di Perrin e di Rutherford, precisamente nello studio del problema della radiazione in una cavità chiusa all'equilibrio termodinamico.

Planck suppose che la radiazione elettromagnetica potesse raggiungere l'equilibrio termodinamico scambiando energia con ipotetici oscillatori materiali non in modo continuo, ma per ‛quanti discreti' hν, dove h deve intendersi come una nuova costante universale e ν è la frequenza dell'oscillatore materiale.

Egli giunse così alla seguente espressione per la densità di energia contenuta in una cavità chiusa, all'equilibrio termodinamico, alla temperatura T e per unità di intervallo di frequenza ν:

In tale espressione, k è la costante di Boltzmann e h è pari a:

h = 6,624•10^-27 erg s.

La legge di Planck è pienamente confermata dall'esperienza, per ogni valore di T e ν per cui è stato possibile eseguire la verifica sperimentale.

Alcuni anni dopo, Einstein (1905) riprese le considerazioni di Planck, ritrovando, per via alquanto diversa e più consistente, lo stesso risultato e giungendo, insieme, all'importante concetto di fotone, di cui diremo poi.

Questa discontinuità, postulata da Planck e poi da Einstein, è del tutto estranea alla fisica classica. Come Bohr provò alcuni anni dopo, essa conduce in modo naturale a postulare che l'energia interna di atomi e molecole possa assumere soltanto valori discreti. Questa idea di Bohr è stata confermata in modo diretto dall'esperienza di Frank e Hertz, mediante lo studio dell'urto anelastico di elettroni contro atomi.

Tuttavia la struttura dei livelli energetici discreti di atomi e, peggio ancora, di molecole non è così semplice come quella postulata da Planck per gli oscillatori armonici materiali, e da Einstein estesa agli oscillatori armonici descriventi il campo elettromagnetico (livelli tutti equidistanti di una quantità hν).

Si ricava un'informazione molto più semplice e fondamentale se, invece di considerare i livelli energetici, si esamina cosa succede nello spazio delle fasi per effetto della quantizzazione. Se si considera per esempio il caso dell'oscillatore armonico, l'esame delle traiettorie del punto che rappresenta classicamente lo stato nello spazio delle fasi mostra che queste sono delle ellissi. Se si impone che i livelli energetici siano quantizzati e l'equidistanza sia hν, si trova immediatamente che l'areola compresa tra due ellissi consecutive è semplicemente h, la stessa per tutti i possibili moti armonici. Tutto va come se lo spazio delle fasi fosse suddiviso in areole uguali ad h. Ciò vale non solo per gli oscillatori, ma si generalizza a sistemi qualunque.

Questo risultato deriva da un principio generale, il cui significato fu scoperto da Heisenberg circa vent'anni dopo i lavori di Einstein, e cioè il cosiddetto ‛principio di indeterminazione'. Secondo il principio di indeterminazione, lo stato dinamico di un sistema non può essere più specificato tramite un punto nello spazio delle fasi, e in generale in uno stato qualunque le variabili dinamiche q e p sono variabili ‛indefinite'. Osserviamo subito che ciò non significa affatto che le variabili siano, per così dire, ‛mal note' ma su questo punto torneremo nel seguito. L'indefinizione Δq di una variabile lagrangiana q, e Δp del suo momento coniugato, sono legate tra di loro dall'universale e fondamentale ‛principio di indeterminazione' di Heisenberg:

(Per l'esatta definizione matematica delle indefinizioni Δp e Δq rimandiamo all'articolo quanti, teoria dei).

Si può facilmente vedere, per esempio, come il principio di indeterminazione di Heisenberg possa permettere di dar ragione della stabilità atomica, contro quanto si inferisce dall'applicazione della meccanica statistica classica al modello di Rutherford.

Infatti, quando il raggio dell'orbita di Rutherford diventa troppo piccolo, il teorema del viriale non può più applicarsi, perché, in virtù del principio di indeterminazione di Heisenberg, l'energia cinetica di un elettrone, se il raggio orbitale è r, non può essere inferiore a ≈ℏ²/2mr² e quindi cresce con l'inverso del quadrato del raggio orbitale. Poiché l'energia potenziale negativa cresce in valore assoluto solo con l'inverso del raggio, l'energia totale ha necessariamente un minimo per distanze finite, quindi l'atomo dev'essere stabile. Se si fa il conto, ad esempio per il caso dell'atomo di idrogeno, si trova che il raggio per cui l'energia è minima ha giust'appunto l'ordine di grandezza del raggio ‛sperimentale' dell'atomo.

Così l'esistenza di h e il principio di indeterminazione di Heisenberg che ne deriva in modo semplice e diretto, dando ragione della stabilità delle proprietà atomiche, danno anche un modo di superare la gravissima fatale deficienza insita nel programma meccanicistico classico, a cui ho accennato nel paragrafo precedente, senza peraltro specificarla.

Non potrei descrivere meglio questa deficienza che con le stesse parole di Heisenberg (v., 1935; tr. it., p. 95): ‟Nondimeno [...] il compito della fisica atomica doveva sembrare insolubile. La chimica tratta infatti di qualità specifiche che in una determinata materia si presentano sempre nella stessa maniera: cioè di qualità che presentano una particolare stabilità di fronte a tutte le possibili perturbazioni [...]. Una simile stabilità è estranea ai sistemi meccanici [...]. Bisognerebbe escogitare qualità ben singolari da attribuire agli atomi se si volesse spiegare meccanicamente una simile stabilità. Questa difficoltà si rivelò nel corso di decenni come il vero problema centrale della fisica atomica, e la sua soluzione riuscì soltanto in base all'ipotesi dei quanti enunciata nel 1900 da Planck".

Prima di proseguire, voglio menzionare che di recente alcuni hanno sollevato delle obiezioni sulla ‛centralità' del problema così impostato. In fondo, si sostiene col loro argomento, tutta la catena di ragionamenti che portano alle difficoltà inerenti alla stabilità interna degli atomi, alla distribuzione della radiazione all'equilibrio termico, ecc., e fondata sull'assunto che, se è valida la meccanica classica, allora debba esser valido anche il principio dell'equipartizione dell'energia. Ma quest'ultimo principio è dedotto anche da ipotesi statistiche, in particolare dalle ipotesi statistiche fatte riguardo alle distribuzioni microcanoniche. Ora, tali ipotesi sono giustificabili, in base alle ricerche fatte sul problema ergodico, solo nel caso in cui lo spazio delle fasi accessibile al moto goda della proprietà della ‛indecomponibilità metrica'. Ma, ad esempio, un insieme di oscillatori armonici, anche lievemente perturbato con piccole perturbazioni anarmoniche, non gode di questa proprietà. Ne seguirebbe che tutta la linea di argomentazioni che abbiamo cercato di esporre precedentemente non è affatto cogente.

Pensiamo che chi argomenta in questo modo non abbia colto in verità il punto essenziale. Se il difetto, in cui cade il principio di equipartizione dell'energia, fosse meramente dovuto a mancanza di ‛indecomponibilità metrica' per i sistemi considerati, si osserverebbe che questi sistemi, invece di raggiungere un unico ben definito stato di equilibrio termodinamico, potrebbero raggiungere diversi stati di equilibrio metastabili (convertibili tramite opportune perturbazioni esterne) e dipendenti dalle condizioni iniziali. Ora, questa non è una situazione che si presenta di fatto; nella realtà si verifica invece un ben definito stato di equilibrio termodinamico; soltanto, questo stato di equilibrio non è quello previsto in base alla meccanica statistica classica, bensì quello che si può prevedere modificando la meccanica classica in modo da tener conto dell'esistenza della costante di Planck h. In altri termini, è lo stato che si può prevedere generalizzando le ipotesi statistiche classiche per adattarle alla nuova meccanica, in modo tale che, nei casi in cui gli effetti della quantizzazione siano trascurabili, si ritrovino gli stessi risultati della meccanica statistica classica.

Ricorderò qui solo che esistono due statistiche quantiche valevoli per due diverse classi di particelle: per le particelle aventi spin, cioè momento angolare intrinseco, semintero, quando espresso in unità ℏ, vale la statistica di Fermi e per le particelle a spin intero vale la statistica di Bose. Di queste statistiche diremo brevemente poi.

Così, per merito della quantizzazione, e tenuto conto che gli elettroni obbediscono alla statistica di Fermi, si sono comprese le proprietà di specifica stabilità degli atomi, le loro proprietà elettromagnetiche, e quindi ottiche, le forze interatomiche, che danno luogo alla formazione di molecole o di solidi, e quindi, almeno in linea di massima, tutte le proprietà di stabilità specifica delle molecole, le loro proprietà elettromagnetiche e, analogamente, le proprietà elastiche, ottiche, elettriche, ecc., dei solidi. Con questo non si vuol dire che tutti i problemi della fisica molecolare, della chimica, della fisica dei solidi e degli altri stati della materia siano risolti. Soltanto, si sono poste basi che si possono considerare sicure per la loro completa soluzione, almeno in via di principio, e molti tra i più importanti dei problemi menzionati sono di fatto risolti almeno approssimativamente. (Non possiamo qui naturalmente entrare in nessun dettaglio. Per questo si rimanda agli articoli quanti, teoria dei; atomo; molecole; criofisica; materia e radiazione interstellare; solidi, fisica dei; biologia molecolare; biofisica; ottica quantistica; meccanica statistica, ecc.). Non si vuole nemmeno dire che tutte queste discipline che studiano il comportamento di corpi macroscopici, o anche di molecole, perfino di molecole abbastanza semplici, siano ormai da considerarsi ‛discipline di second'ordine'; ché la comprensione dei fenomeni che esse studiano (i quali d'altra parte possono essere talvolta molto complessi e di grandissimo interesse intrinseco) può richiedere una originalità di pensiero paragonabile a quella necessaria per avanzare, per esempio, sulla ‛frontiera' della ‛fisica delle particelle elementari'. Si vuole solo dire che tutti gli oggetti fisici che sono studiati in tutte queste discipline, e cioè nella fisica atomica, nella fisica molecolare, nella chimica, nella fisica dei solidi, nella fisica dei fluidi, ecc., sono caratterizzati da un unico tipo di interazione, sufficiente a descriverne il comportamento: l'interazione elettromagnetica (se, ben inteso, si tiene conto degli effetti della quantizzazione).

Si giunge in questo modo a una grandiosa unificazione di svariatissimi rami della scienza, non solo della fisica, ma della chimica e della parte più fondamentale della biologia, la biologia molecolare, con risultati che hanno dato, tra l'altro, la prima conferma decisiva della teoria dell'evoluzione.

c) Dualità corpuscolare-ondulatoria

Naturalmente, l'introduzione della discontinuità, imposta dalla costante h, in un edificio quale quello della fisica classica che fa uso essenziale, per profonde ragioni di metodo, come vedremo, di quantità continue, non poteva avvenire senza una profonda rivoluzione concettuale nelle basi stesse della fisica; rivoluzione che, in un certo senso, coinvolge l'assetto metodologico e il significato di tutta la scienza naturale. Il primo sintomo della necessità di una tale profonda rivoluzione si è rivelato con la già ricordata introduzione da parte di Einstein del concetto di fotone. Nella sua deduzione della legge di Planck, Einstein non si limitò a considerare gli scambi di energia tra materia e radiazione, ma considerò anche gli scambi di quantità di moto. Nella deduzione di Einstein, si noti bene, era implicita l'ipotesi che la quantità di moto degli atomi che emettono o assorbono radiazione sia ben definita, tanto prima quanto dopo l'atto di assorbimento e di emissione. In base a tale ipotesi, Einstein giunse alla conclusione che la radiazione deve essere emessa dall'atomo, in un atto di emissione, non solo con una ben definita energia, hν, ma anche con una quantità di moto ben determinata (hν/c) avente una ben definita direzione (Niedelstrahlung). Ciò equivaleva a risuscitare il modello corpuscolare della luce, e i ‛corpuscoli luminiferi' furono chiamati ‛fotoni'. Così il modello corpuscolare della luce sembrava in certo modo imposto dalla quantizzazione, e riceveva del resto numerose conferme sperimentali (effetto fotoelettrico; effetto Compton; più di recente l'effetto Mössbauer, che conferma direttamente l'idea della Niedelstrahlung; ecc.).

Sorgeva allora immediatamente il problema: come interpretare gli effetti di interferenza che, viceversa, avevano imposto - in un modo che nel secolo passato si era ritenuto definitivo - il modello ondulatorio della luce?

Il problema presentava aspetti paradossali, e vale la pena di riesaminarli brevemente.

Consideriamo ad esempio l'esperienza dell'interferenza della luce, eseguita mediante un interferometro di Michelson. Supponiamo che le frange si formino sopra una lastra fotografica, considerata come una lastra ideale con rendimento pari a 1, ossia ammettiamo che ogni singolo fotone sia sicuramente rivelato. Supponiamo che l'intensità della luce monocromatica usata sia molto bassa. Noi vedremmo ora un granulo sensibile, ora l'altro, impressionato dalla luce incidente: ad ogni granulo corrisponde un fotone che sembra giungere in un posto ben determinato; solo dopo un tempo considerevole potremo riconoscere che la densità del numero dei granuli impressionati varia sulla superficie della lastra, dando luogo all'apparizione delle classiche frange d'interferenza. Ciò suggerisce immediatamente di collegare l'aspetto corpuscolare e quello ondulatorio della radiazione tramite un'ipotesi statistica: è il numero medio dei fotoni che cadono su una data superficie che è proporzionale all'energia che cade su quella superficie calcolata secondo le leggi dell'ottica ondulatoria. Se il fotone è uno solo, potremo parlare soltanto di probabilità che il fotone venga assorbito entro una data areola della lastra, e questa probabilità sarà proporzionale al modulo quadrato dell'ampiezza dell'onda incidente. Del resto, considerazioni probabilistiche erano già entrate in modo essenziale nella teoria einsteiniana che aveva condotto al concetto di fotone. Tuttavia questa stessa interpretazione probabilistica presenta degli aspetti paradossali se si considera il fotone come una particella classica. Infatti, in questo caso, dovremmo dire che ogni singolo fotone, incidendo sullo specchio semitrasparente dell'interferometro, sarà o riflesso o trasmesso. D'altra parte i singoli fotoni provenienti da una normale sorgente viaggiano in modo indipendente (e ciò è confermato da esperienze dirette). Ogni fotone va considerato isolatamente e, quindi, trattandosi di eventi mutuamente escludentisi, secondo un noto teorema del calcolo delle probabilità, la probabilità di osservare l'assorbimento del fotone in un'areola Δs dovrebbe essere uguale alla somma della probabilità che ha il fotone di essere assorbito in Δs nel caso in cui sia riflesso, più quella nel caso in cui sia trasmesso dal separatore d'onde. Ma, se così fosse, non si osserverebbero frange d'interferenza.

La difficoltà è tale che indusse Bohr, Kramers e Slater a formulare una teoria in cui la questione sul percorso del fotone perdesse completamente senso in ogni caso. Per questo, però, è necessario supporre che nei singoli processi elementari in cui interviene un singolo fotone le leggi di conservazione dell'energia e dell'impulso siano violate, e siano anch'esse leggi statistiche, valide solo per i grandi numeri. Infatti, se non è così, si può decidere in linea di principio se il fotone è riflesso o trasmesso: basta osservare se lo specchio rincula o no; se rincula, è riflesso; se no, è trasmesso. Immediatamente furono intraprese delle ricerche sperimentali, per verificare se la legge della conservazione dell'energia e dell'impulso è valida o no nei processi elementari, usando l'effetto Compton. Esperienze di Bothe e Geiger e di Compton e Simon (v. quanti, teoria dei) provarono che la legge di conservazione è valida in ogni singolo processo elementare (qualora, naturalmente, le grandezze che si misurano siano ben definite). La difficoltà così si ripresenta in pieno. La soluzione sta nel principio di indeterminazione; se si vuol stabilire se lo specchio semitrasparente rincula o no, occorre che la sua quantità di moto sia definita in modo sufficientemente preciso prima dell'arrivo del fotone. Ma in questo caso la sua posizione deve avere una certa indefinizione, maggiore o uguale al limite inferiore stabilito dal principio di indeterminazione. Con una tale indefinizione è facile vedere che scompaiono le frange: scompare così anche il paradosso.

L'analisi di questa e di molte altre simili situazioni condusse Bohr al suo celebre ‛principio di complementarità', secondo cui la realtà quantica presenta aspetti che sono tra di loro incompatibili dal punto di vista classico. Questi aspetti però non si presentano mai assieme, per cui vere e proprie antinomie possono essere sempre evitate. L'aspetto corpuscolare e quello ondulatorio della radiazione sono due aspetti complementari, secondo Bohr. Tale complementarità non è propria solo della radiazione, ma anche della ‛materia'. Così si possono osservare effetti interferenziali con elettroni, protoni, neutroni, atomi e molecole.

Come abbiamo già detto, lo stesso principio di indeterminazione implica che lo stato dinamico di un sistema non possa più essere rappresentato tramite un punto nello spazio delle fasi. Data l'esistenza dei fenomeni interferenziali, si è trovato conveniente, invece, rappresentarlo tramite una ‛funzione d'onda' (v. quanti, teoria dei) la quale obbedisce a un'equazione differenziale di propagazione che, appunto allo scopo di permettere l'interpretazione dei fenomeni interferenziali, deve essere un'equazione lineare, la cosiddetta equazione di Schrödinger:

In questa equazione ψ rappresenta la funzione d'onda, H è un operatore lineare hermitiano che, nella nuova meccanica quantica, rappresenta l'hamiltoniana del sistema e t è il tempo. Nella nuova meccanica quantica anche le q e le p sono rappresentate da operatori lineari hermitiani non commutabili (v. quanti, teoria dei). L'operatore H, nel caso dei sistemi che abbiano un corrispondente classico, è una funzione delle q e delle p formalmente uguale alla funzione H classica, a parte la specificazione eventuale dell'ordine dei fattori nel prodotto di operatori non commutabili.

Vi è così una stretta corrispondenza formale tra la meccanica quantica e la meccanica classica nella sua forma canonica o hamiltoniana. Per esempio, se si risolve la (12) nell'approssimazione dell'ottica geometrica, la ‛fase' della ψ moltiplicata per ℏ corrisponde all'azione di Hamilton. Questa corrispondenza non deve meravigliare se si ricorda quanto già avevamo detto a proposito del formalismo canonico nel capitolo precedente.

La risoluzione delle equazioni del moto nella meccanica classica ci permette di descrivere come varia lo stato di un sistema in funzione del tempo; analogamente, la soluzione dell'equazione (12) ci permette di descrivere come varia la funzione d'onda che rappresenta lo stato del sistema in funzione del tempo. Vi è però una differenza essenziale tra il caso della meccanica quantica e quello della meccanica classica. In quest'ultimo, la variazione dello stato di un sistema non è sempre rappresentata meramente dalla soluzione della (12). Occorre ammettere che gli stati quantici possano subire delle variazioni brusche e irreversibili che prendono luogo in ben specificabili circostanze, ad esempio molto spesso all'atto di effettuare delle misure di grandezze osservabili. Tali variazioni brusche si chiamano ‛processi di contrazione o riduzione degli stati'. Si consideri per esempio l'emissione di un fotone da parte di un atomo situato in una posizione abbastanza ben localizzata, e per il quale quindi la quantità di moto è indefinita. La funzione d'onda che rappresenta lo stato del fotone avrà una rappresentazione spazio-temporale simile a quella di un'onda classica (per es., un'onda sferica di dipolo). Supponiamo ora di sapere che il fotone subisce l'effetto Compton interagendo con un elettrone che sia anch'esso abbastanza ben localizzato nello spazio; in questo processo l'onda dovrà bruscamente ridursi in un ristretto intorno della zona occupata dall'elettrone. È nel processo di riduzione che interviene il carattere statistico della meccanica quantica, e si utilizza la conoscenza della funzione d'onda precisamente per calcolare la probabilità del processo di riduzione stesso, nella maniera che è descritta nell'articolo quanti, teoria dei.

Il processo di riduzione, essendo ‛essenzialmente' irreversibile, toglie ogni significato al paradosso di Loschmidt (v. sopra, cap. 2, Èc).

Prima di chiudere questo argomento, aggiungerò solo che, quando il sistema il cui stato è descritto dalla funzione d'onda ψ sia composto di N particelle identiche, si hanno fondamentalmente solo due possibilità compatibili in modo naturale con il formalismo e le regole interpretative della meccanica quantica: a) la funzione ψ è antisimmetrica rispetto allo scambio delle coordinate (tutte le coordinate, sia ‛interne' sia ‛esterne') delle singole particelle; b) la funzione ψ è simmetrica rispetto a un tale scambio.

Il primo caso conduce alla statistica di Fermi, il secondo alla statistica di Bose.

d) Fisica del nucleo; interazioni forti e deboli; fisica delle particelle elementari

A parte alcuni fenomeni abbastanza sottili, come per esempio la struttura iperfine degli spettri atomici, la quale dipende dai momenti magnetici nucleari, o come la struttura degli spettri ottici di molecole biatomiche omonucleari, la quale dipende dalle proprietà di simmetria per scambio dei nuclei (se obbediscono alla statistica di Fermi o a quella di Bose), il ‛grosso' della fisica atomica, della fisica molecolare, della fisica dei solidi, della chimica, ecc. si può costruire considerando i nuclei come particelle puntiformi dotate di una certa massa e di una certa carica Ze dove Z è un numero intero (numero atomico) ed e è la carica del protone (nucleo di idrogeno).

Ma prima ancora che i nuclei fossero scoperti, era stato scoperto il fenomeno della radioattività naturale, il quale doveva condurre, insieme ad altri fatti, alla conclusione che i nuclei hanno una struttura interna.

Un passo decisivo verso la comprensione di tali strutture venne compiuto nel 1932 con la scoperta del neutrone (v. neutroni). Si riconobbe così che i nuclei sono particelle composte solo di protoni e neutroni. Si riconobbe però anche che il campo elettromagnetico non può da solo rendere conto nè dell'esistenza dei nuclei (ché, anzi, costituisce un fattore il quale limita la possibilità di esistenza di nuclei con Z molto elevato, per effetto della repulsione elettrostatica), nè di tutte le trasmutazioni nucleari, tra le quali proprio alcune di quelle dovute alla radioattività naturale.

Ciò dà luogo a una differenza essenziale tra la fisica del nucleo e la fisica, diciamo così, ‛extranucleare', nella quale, come abbiamo detto, il campo elettromagnetico (e quello gravitazionale, se intervengono grandi masse) basta a render conto di tutti i fenomeni.

È stato necessario introdurre due nuove interazioni: la cosiddetta ‛interazione debole' (Fermi, nel 1934), per render conto della radioattività β, e la ‛interazione forte' (Yukawa, nel 1935) per render conto del legame che unisce i nucleoni, cioè protoni e neutroni, a formare un nucleo composto.

Le denominazioni ‛forte' e ‛debole' provengono dal confronto con l'interazione del campo elettromagnetico, caratterizzata dalla carica dell'elettrone il cui quadrato, nelle ‛unità naturali' in cui ℏ = 1 e c = 1, è un numero puro che vale circa 1/137 (la cosiddetta costante di struttura fine α = e²/ℏc).

L'interazione debole non ha una costante di accoppiamento adimensionale: le dimensioni di questa costante sono quelle dell'inverso del quadrato di una massa. Assumendo come unità di massa quella M del nucleone, il quadrato della costante di accoppiamento debole f² risulta uguale circa a 10^-10 (ℏ = 1, c = 1, M = 1).

Il quadrato della costante di accoppiamento per l'interazione forte g², definito in modo opportuno (sfruttando una certa analogia tra diffusione del pione ed effetto Compton), risulta dell'ordine di 15.

Le teorie sia di interazione forte che di interazione debole sono state confortate da importanti successi in alcune delle loro previsioni per le interazioni forti nomineremo la previsione dell'esistenza dei pioni (v. particelle elementari), per le interazioni deboli ndmineremo la previsione dell'esistenza del neutrino - e hanno dato luogo a importanti sviluppi sia nella fisica nucleare, sia nell'astrofisica, sia nella fisica delle particelle elementari.

Per quanto riguarda la fisica nucleare, i successi più importanti furono dovuti all'applicazione di certi principi di simmetria: simmetria esterna gruppo delle rotazioni spaziali - e simmetria interna connessa al cosiddetto spin isotopico (Heisenberg, nel 1932), simmetrie (v. simmetrie e invarianze) entrambe descrivibili tramite rappresentazioni del gruppo SU₂ (Wigner, nel 1940).

D'altra parte, l'insufficiente conoscenza delle interazioni forti ha impedito che anche il più semplice problema dinamico della fisica del nucleo - cioè quello del deutone, che è equivalente al problema dell'atomo di idrogeno nella fisica atomica - fosse risolto fino in fondo noi non conosciamo tutt'oggi la ‛vera' funzione d'onda del deutone.

Applicazioni fondamentali della fisica nucleare sono state fatte in astrofisica. La sorgente di gran lunga più importante di energia per le stelle che appartengono, come il Sole, alla cosiddetta sequenza principale, fu identificata (Bethe e Critchfield, nel 1938) con la reazione di fusione dell'idrogeno:

H + H → D + e⁺ + ν

(D è un deutone, e⁺ è un elettrone positivo e ν è un neutrino) e la susseguente reazione di fusione del deuterio che poi dà luogo ad elio e libera effettivamente la maggior parte dell'energia.

Si noti che la reazione che produce deuterio implica l'emissione di un positrone, quindi ‛decadimento β', ossia l'interazione debole. Per questo il ‛fuoco solare' brucia in modo lento e tranquillo: ne risulta una vita media del Sole dell'ordine di 10¹¹ anni che è in accordo con numerosi fatti sperimentali relativi all'età del sistema solare.

Seguendo l'evoluzione stellare (v. stelle), si riconosce che, tramite successive fusioni a temperature sempre più alte, si producono nuclei di peso sempre maggiore fino al ⁵⁶Fe. La formazione di elementi più pesanti può aver luogo principalmente durante fenomeni di tipo esplosivo (esplosioni di supernove). Si può dar così conto, in modo abbastanza attendibile, dell'abbondanza relativa colla quale vengono trovati gli isotopi degli elementi naturali, anche i più pesanti, nell'universo.

Fino a questo punto il quadro che abbiamo fatto della fisica del Novecento appare in certo senso piuttosto trionfalista. Abbiamo posto in rilievo come si sia raggiunta una straordinaria unificazione del sapere scientifico che va dall'astrofisica alla chimica e perfino a certe parti fondamentali della biologia, quale nel secolo passato poteva essere solo sognata, ma difficilmente supposta su basi veramente concrete.

Dobbiamo ora prospettare i limiti di questo trionfo e così facendo delineare qual è la ‛nuova frontiera' della fisica.

È essenziale premettere un'osservazione. La maggior parte della fisica del Novecento si basa su due teorie fondamentali: la meccanica quantica e la teoria della relatività ristretta. Ora in queste teorie entrano in modo ‛strutturale' solo due costanti: ℏ per la meccanica quantica, c per la relatività. Con questo vogliamo dire che, per esempio, la relatività sarebbe inconcepibile se non esistesse c come velocità limite; come tale, c deve essere ben determinata e unica. Analogamente ℏ, per mantenere un senso al principio di indeterminazione, deve essere ben determinata e unica.

D'altra parte, nella nostra fisica, entrano tante altre costanti essenziali per la descrizione del mondo, come la carica dell'elettrone, il rapporto della massa dell'elettrone a quella del protone, le costanti che caratterizzano le interazioni forti e quelle deboli, ecc.

Dico che queste sono costanti essenziali alla descrizione del mondo con buone ragioni: il mondo sarebbe essenzialmente diverso anche per piccole variazioni del valore di talune di queste costanti. Per esempio, se l'interazione forte fosse un po' più forte di quello che è, potrebbe esistere uno stato legato ²He formato da due soli protoni; in tal caso la reazione di fusione dell'idrogeno leggero, che dà luogo poi alla formazione di elio e al massimo sviluppo di energia stellare, procederebbe in modo molto più rapido perché la disintegrazione β in ogni caso occorrente potrebbe avvenire a partire dallo stato legato ²He anziché durante l'urto protone-protone. Ciò renderebbe impossibile il formarsi di sistemi planetari come quello in cui noi viviamo e quindi la vita come noi la conosciamo. Lo stesso dicasi se l'interazione debole fosse un po' più forte. Se poi la carica elettrica elementare fosse più grande, la curva di stabilità dei nuclei sarebbe diversa perché la repulsione coulombiana sarebbe molto più importante e gli elementi stabili sarebbero in numero molto più ridotto di quelli che noi conosciamo. Inoltre la chimica, la fisica dei solidi, ecc., sarebbero assai diverse da quelle che conosciamo.

Ora, tutte queste costanti così importanti per la conoscenza del mondo empirico non entrano però ‛strutturalmente' nella nostra presente teoria, ma vi debbono essere introdotte dal di fuori, come suol dirsi, ‛a mano'.

Per esempio, non si sa perché α, la costante di struttura fine, abbia il valore che ha, né perché questo valore debba essere unico; tant'è vero che in teorie abbastanza recenti della struttura delle particelle elementari si è ipotizzata l'esistenza di particelle (i quarks) con cariche ±1/3e e ±2/3e. Nemmeno la struttura atomica della materia è pienamente giustificata nell'ambito delle nostre attuali conoscenze: possiamo dar ragione della stabilità degli atomi e di tutte le loro altre proprietà, una volta noto che gli atomi hanno la costituzione che hanno e che la carica e lo spin dell'elettrone sono quelli che sono. Ma se la carica dell'elettrone fosse per esempio molto maggiore, non solo gli atomi sarebbero diversi; potrebbero non esistere neanche particelle analoghe agli atomi che conosciamo.

Ma v'ha di più. Landau e Peierls, nel 1931, hanno posto in forse la consistenza dell'elettrodinamica quantica anche in assenza di interazione. Essi pensavano di aver mostrato che singole componenti del campo elettromagnetico non possono mai essere completamente definite come quantità osservabili nel senso della meccanica quantica, contrariamente a quanto richiedono le regole interpretative della meccanica quantica stessa. Bohr e Rosenfeld hanno successivamente mostrato che in realtà quanto sostenevano Landau e Peierls non era del tutto corretto e che l'elettrodinamica quantica, in assenza di interazione, è una teoria perfettamente consistente. Per far questo, però, hanno dovuto escogitare ‛espenenze ideali', in cui si fa uso per esempio del concetto di corpi piccoli a piacere, con densità di massa e densità di carica grandi a piacere e richiamabili verso certe posizioni di equilibrio da forze perfettamente elastiche. In tutto ciò si trascura completamente quanto sappiamo sulla struttura dell'usuale materia, e si immagina, con la massima libertà, la possibilità di esistenza di una materia anche profondamente diversa da quella che conosciamo, preoccupandosi soltanto che essa obbedisca alle leggi della relatività ristretta e della meccanica quantica. Ciò, beninteso, è perfettamente legittimo dati gli scopi che Bohr e Rosenfeld si proponevano; anzi, non si potrebbero nemmeno discutere le limitazioni imposte alla misurabilità di date grandezze da una certa struttura della materia, se non nel quadro di una teoria veramente fondamentale di tale struttura, in cui le costanti caratteristiche della materia entrino in modo necessario e non siano introdotte dal di fuori.

Ma proprio per ciò, questo esempio fra gli altri mostra che le questioni a cui abbiamo accennato non solo sono suggerite da un legittimo desiderio di approfondire le fondamenta del peraltro splendido edificio delle attuali conoscenze scientifiche, ma riguardano la consistenza stessa di tali fondamenta, e precisamente la consistenza degli essenziali dati empirici che noi introduciamo a mano con il quadro quantistico e relativistico nel quale vogliamo introdurli.

Il fatto che su tali incerte basi noi possiamo costruire un edificio meraviglioso non potrebbe rassicurare completamente che un assoluto pragmatista, il quale si rifiutasse di pensare quando ciò risultasse scomodo.

L'indagine sui fondamenti della struttura della materia si svolge oggi nella cosiddetta fisica delle particelle elementari.

Per una doppia serie di ragioni, una tale fisica deve essere quantica e relativistica insieme, non separatamente quantica, ovvero relativistica, come in altri campi meno fondamentali della fisica.

La prima serie di ragioni ha attinenza con le simmetrie relative al gruppo di Lorentz inomogeneo (v. quanti, teoria dei) e ad altre semplici fondamentali simmetrie che in modo del tutto naturale allargano il gruppo di Lorentz: la cosiddetta riflessione spaziale (P), la inversione temporale (T) e infine una simmetria che si presenta naturale nelle teorie ‛quantum-relativistiche', e cioè la coniugazione di carica (C) (v. particelle elementari).

Sulla base di queste simmetrie, sono stati ottenuti due importantissimi risultati teorici: a) la previsione dell'esistenza dell'antimateria, pienamente confermata dall'esperienza; b) la connessione, già stabilita empiricamente, come avevamo detto, tra spin e statistica.

A vero dire, P, C, e T stabiliscono delle limitazioni per le possibili interazioni fra particelle elementari, e si è trovato che P e C sono totalmente violate dall'interazione debole (Yang e Lee, 1957), mentre più di recente, nella fisica dei mesoni K e É, si è dimostrato che anche T è violato per opera di un'interazione ultradebole.

Fortunatamente, per stabilire i suddetti risultati fondamentali su materia-antimateria e spin-statistica, basta che non sia violato il prodotto PTC delle tre simmetrie, e per ora almeno non c'è la minima evidenza che PTC sia violato. Se si trovasse una tal violazione, occorrerebbe probabilmente cercare qual è il ‛vero fondamento' dei nostri risultati fondamentali. Verrebbe così posto in dubbio uno dei grossi argomenti (l'altro è il successo dell'elettrodinamica quantica) che abbiamo per credere all'attuale quadro quantum-relativistico per una teoria delle particelle elementari.

La seconda serie di ragioni di cui dicevamo riguarda il modo in cui le particelle elementari interagiscono.

È forse bene, per comprendere questo argomento, riflettere su una distinzione almeno fenomenologica (da un punto di vista teorico fondamentale la cosa sarebbe assai ardua) che possiamo porre tra particelle elementari e particelle composte.

Consideriamo un sistema costituito da un atomo di ⁴He inizialmente neutro nello stato fondamentale e da un elettrone, al quale, mediante intervento di un campo esterno, potremo meramente ‛pompare' quanta energia vorremo e quante volte vorremo.

In quel che segue, per semplificare le cose, trascureremo la possibilità di emissione di radiazione elettromagnetica e la creazione di coppie e^-, e⁺.

Supponiamo dapprima di dare all'elettrone un'energia di 10 eV e studiamo l'urto elettrone-elio. Possiamo ripetere l'esperimento quante volte vogliamo. L'urto sarà meramente elastico. Il sistema si comporterà come se avesse solo 7 gradi di libertà, dei quali 4 per l'elettrone (a causa dello spin) e 3 per l'atomo. Sappiamo che per quest'ultimo ciò è un effetto della quantizzazione.

Portiamo ora l'energia del nostro proiettile a 100 eV e ripetiamo più volte l'esperimento d'urto. L'atomo d'elio perderà prima un elettrone e poi un altro. Ma poi, per quante volte ripetiamo il bombardamento, con l'elettrone a 100 eV, non accadrà più nulla al di fuori di urti elastici; nessun altro elettrone sarà strappato.

Anche se aumentiamo l'energia del proiettile, non succederà niente di nuovo finché non raggiungiamo un'energia di circa 20 MeV: allora il nucleo di elio si disintegrerà e darà luogo, finalmente, dopo urti ripetuti, a due protoni e due neutroni. Ma ancora una volta, se si ripeterà quante volte si vuole il bombardamento, per esempio contro un protone con un elettrone da 20 MeV, supponendo di aver tolto gli altri oggetti dal campo sperimentale, non accadrà nulla.

Solo aumentando di nuovo l'energia fino a circa 150 MeV si potrà osservare l'emissione di un pione positivo o neutro, a spese di quasi tutta l'energia cinetica dell'elettrone.

La cosa potrebbe sembrare analoga a quanto avveniva nei casi precedenti.

Questa volta, però, vi è una differenza drammatica ed essenziale. Ripompando ogni volta energia all'elettrone, fino al limite di circa 150 MeV, possiamo bombardare ripetutamente il nucleone rimasto (neutrone o protone) e ottenere quanti pioni vogliamo. Possiamo sempre arrestare il processo, anche dopo aver ottenuto un grande numero di pioni, quando il nucleone sia un protone indistinguibile da quello da cui siamo partiti. È questa circostanza che ci fa ritenere che il numero di pioni che così possiamo ottenere sia illimitato.

Poiché alla fine sia l'obiettivo bombardato sia il proiettile sono in se stessi rimasti immutati, donde sono venuti i pioni che si osservano? Evidentemente sono stati ‛creati' a spese dell'energia cinetica del proiettile.

Questo processo, che implica la trasformazione di energia cinetica in energia di massa (anche massa di riposo) di nuove particelle, è un processo eminentemente relativistico. Non si tratta più del mero decomporsi di un oggetto nei suoi componenti ‛preesistenti', come accade nei casi visti in precedenza. Per la sua indefinita ripetibilità, esso mette d'altra parte in gioco un numero apparentemente illimitato di gradi di libertà. Ciò però non deve meravigliare perché la teoria della relatività, escludendo ogni azione a distanza, sembra dover naturalmente servirsi solo di interazioni ‛locali' tra campi, ossia tra sistemi con infiniti gradi di libertà (v. sopra, cap. 2).

Pertanto, quando si arrivi a particelle che non si possono più fenomenologicamente considerare composte, appare naturale che le interazioni debbano essere essenzialmente descritte tramite campi e in modo relativistico.

Del resto l'elettrodinamica quantica, ossia la teoria quantica del campo elettromagnetico, includente l'interazione di tale campo con gli elettroni, è un esempio di teoria quantizzata di campo, l'unico, d'altra parte, che sia ben noto e, da un certo punto di vista, ben fondato.

Le altre teorie quantiche di campi sono essenzialmente basate sull'analogia con l'elettrodinamica quantica. I successi dell'elettrodinamica quantica sono stati notevolissimi e le previsioni di tale teoria e i risultati sperimentali, in accordo tra di loro entro gli errori, sono tra i più raffinati di tutta la fisica. Tuttavia nemmeno l'elettrodinamica quantica sfugge a un ‛morbo di fondo' di tutte le teorie quantiche di campo: le cosiddette ‛divergenze', che sono proprio dovute al numero infinito di gradi di libertà del sistema in studio.

L'elettrodinamica quantica riesce però ad aggirare queste difficoltà per merito di due concomitanti circostanze: 1) la piccolezza della costante di interazione (α, la costante di struttura fine) per cui si può trascurare tale interazione in approssimazione zero (e così si fa per esempio nella teoria dei livelli energetici atomici); si può poi introdurre l'interazione come piccola perturbazione in un secondo tempo; 2) la particolare struttura della teoria per cui, nelle approssimazioni via via più elevate del metodo perturbativo, le divergenze possono essere isolate e poi sottratte con la duplice tecnica associata della ‛regolarizzazione e rinormalizzazione' (v. particelle elementari).

Il problema di fondo, però, è insoluto anche per l'elettrodinamica quantica.

Per le altre interazioni, le deboli e le forti, a parte il fatto che esse non descrivono campi classici, e non sono quindi fondate direttamente sulla ‛corrispondenza' con casi classici, la situazione è anche formalmente assai peggiore. Per le interazioni forti, il metodo perturbativo non si può affatto applicare. Per le interazioni deboli, la teoria nella forma primitivamente proposta da Fermi non è rinormalizzabile. Recentemente, nell'intento principale di unificare la teoria dell'elettromagnetismo con quella delle interazioni deboli, sono stati proposti modelli di teorie che sono anche rinormalizzabili. Certo, la unificazione dell'elettromagnetismo con le interazioni deboli sarebbe di grandissima importanza; d'altra parte però i modelli finora proposti non sono ancora univocamente definiti e fanno uso dell'ipotesi dell'esistenza di nuove particelle (mesoni vettoriali) che non è possibile osservare sperimentalmente con i mezzi attuali, perché dotate di massa molto elevata. La scoperta sperimentale di tali particelle corroborerebbe in modo probabilmente decisivo queste teorie. Per il momento però appare difficile formulare un giudizio definitivo su questi tentativi. D'altra parte il carattere fenomenologico della distinzione delle varie interazioni in forti, elettromagnetiche, deboli e gravitazionali, appare piuttosto probabile.

Queste essendo le difficoltà di fondo delle teorie, non deve meravigliare il fatto che la ricerca sperimentale, la quale viene condotta in modo molto costoso e faticoso accelerando particelle ad alta energia - si tratta di fisica relativistica e ultrarelativistica - conduca molto spesso a risultati insospettati, se si fa eccezione dell'importantissima scoperta dell'antimateria, ma non ancora molto illuminanti.

Certo, tali risultati hanno suggerito importanti progressi teorici, soprattutto per quanto riguarda alcune simmetrie interne, sia delle interazioni forti sia delle interazioni deboli, ma fino ad oggi almeno non appare che il raggiungimento degli scopi fondamentali della ricerca sulle particelle elementari sia vicino (v. particelle elementari).

Sembra che si possa dire che, con la scoperta dell'elettrone, del protone e del neutrone, un più che secolare processo di analisi della materia in componenti ‛preesistenti' sempre più minute sia giunto al termine. Non è però giunta al termine l'analisi della struttura della materia. Si sono raggiunte, sembra, delle ‛colonne d'Ercole' e si sono appena oltrepassate per esplorare un oceano quasi totalmente nuovo e che appare sconfinato e misterioso: là si debbono trovare le risposte ai perché fondamentali che poco sopra ci andavamo chiedendo, ma ancora non sappiamo a quale profondità, né se le nostre forze basteranno a trovarle.

Ciò ha contribuito a modificare piuttosto notevolmente il carattere della ricerca fondamentale dopo l'ultima guerra mondiale: la ricerca, per i mezzi ingenti che richiede, ha assunto un carattere semindustriale, e i ricercatori, soprattutto gli sperimentali, si debbono sottoporre a una disciplina semindustriale. D'altra parte, l'avarizia con la quale la natura concede i risultati rispetto agli sforzi umani impiegati rende spesso deludente e frustrante il lavoro dei ricercatori. Nonostante questo, tale lavoro va fermamente proseguito nella speranza che qualche nuova idea teorica o sperimentale, o semplicemente qualche risultato veramente illuminante, permetta di fare qualche progresso decisivo.

Ancora un'osservazione: oltre al campo elettromagnetico conosciamo un altro campo classico, quello gravitazionale. Nessun tentativo di quantizzare il campo gravitazionale può veramente dirsi riuscito. A proposito di particelle elementari e gravitazione, si sono anzi ventilate idee abbastanza strane: per esempio che l'antimateria possa sentire la gravitazione con segno opposto a quello della materia. Ciò non solo contraddice la teoria della relatività generale, ma direttamente anche l'esperienza: il fotone infatti è autoconiugato per l'operazione particella⇄antiparticella, e la luce è, come sappiamo, deviata da un campo gravitazionale.

4. Questioni di metodo e di valore

a) Obiettività e arbitrarietà; errori di misura e indefinizione

Dobbiamo ora riprendere alcune questioni, a cui abbiamo accennato nell'introduzione, relative all'oggetto, al metodo e al valore della scienza della natura e della fisica in particolare. Ciò è reso opportuno dalla rivoluzione concettuale introdotta nelle basi della scienza dalla fisica del Novecento, particolarmente dalla meccanica quantica.

Per quanto abbiamo detto, scopo della scienza è una descrizione obiettiva, secondo la definizione di Poincaré, e possibilmente unitaria, del mondo empirico.

Se una descrizione della esperienza, che sia obiettiva, possa anche essere in qualche senso esauriente, è questione che riguarda la filosofia e che qui non tratteremo. Tuttavia una concreta (non ideale) descrizione obiettiva di una data situazione empirica non può essere esauriente perché essa può essere obiettiva solo a patto di essere approssimata. Supponiamo infatti che la descrizione in questione implichi delle misure (in caso opposto le nostre argomentazioni varranno a fortiori); in generale, i risultati delle misure delle stesse grandezze, fatte da diversi osservatori, non saranno identici.

Tuttavia si dirà ugualmente che la descrizione è stata controllata in modo obiettivo, se la differenza tra i vari valori corrispondenti alle stesse grandezze saranno ‛entro' o ‛non supereranno di molto' gli errori di misura.

Se per essere ‛comuni' ai vari osservatori i risultati dovessero essere identici, la condizione di obiettività non sarebbe mai soddisfatta se non eccezionalmente e per caso. L'obiettività si raggiunge trascurando differenze dell'ordine dell'errore. Queste differenze, d'altra parte, entrano nei dati bruti dell'esperienza, ma debbono essere considerate irrilevanti. Per ciò stesso, la descrizione obiettiva non è esauriente, ancorché essa contenga, oltre che l'indicazione del risultato della misura, anche quella dell'errore.

Ma non è allora il concetto stesso di obiettività arbitrario? La cosa va approfondita. Anche l'errore può essere definito in modo obiettivo, però anch'esso approssimato; anzi, l'approssimazione relativa con cui è definito l'errore è assai peggiore in generale di quella con cui è definita la grandezza misurata.

Potrebbe perfino sorgere il dubbio di trovarsi di fronte all'ennesimo esempio di ‛regresso all'infinito'. In pratica però ci si arresta generalmente alla discussione dell'errore e si assegna un limite superiore che le differenze tra diverse misure debbono superare per essere considerate differenze significative, da tre a cinque volte l'errore standard a seconda della severità del criterio.

Ciò naturalmente comporta un certo grado di arbitrarietà, anzi, formalmente, di dogmatismo. Di fatto, ciò non è dogmatico nè alla fine arbitrario perché, se necessario, e ove si presentino delle buone ragioni, ogni risultato sperimentale è sempre soggetto a revisione.

Inoltre, il processo di continuo raffinamento dei metodi di misura potrebbe far pensare che, alla fine, almeno in via di principio, si possa eliminare ogni arbitrarietà nella definizione empirica di una grandezza.

Per esempio, supponiamo di voler misurare la distanza tra i bordi interni di due sottili tratti paralleli tracciati su una sbarra di acciaio. Possiamo usare un regolo graduato, con graduazioni di un millimetro, e misurare tale distanza con un errore di qualche decimo di millimetro, a parte errori sistematici che supponiamo eliminabili. Poi possiamo usare un calibro con verniero e misurare la stessa distanza con un errore di qualche centesimo di millimetro; e poi un comparatore munito di microscopio e ripetere la misura con un errore di qualche micron. Se le misure sono ben fatte, quelle più precise differiscono da quelle meno precise per non più dell'errore di queste ultime. Inoltre, essendo l'errore delle misure più precise molto piccolo rispetto a quello delle misure meno precise, la differenza dà l'errore vero delle meno precise, con una correttezza tale che l'arbitrarietà dovuta alla stima dell'errore delle misure più precise è irrilevante ogni qualvolta l'errore delle misure più precise è tollerabile. Si può obiettare che l'arbitrarietà sarà praticamente irrilevante, ma l'obiezione di principio permane.

Ma anche l'obiezione di principio cade se si pensa, giustappunto in via di principio, a un processo di limite mediante tecniche successive sempre più raffinate, in cui il limite dell'errore sia nullo. Per questo, però, è necessario che la grandezza misurata sia in se stessa ben definita. Torneremo su questo importante punto.

Ora vogliamo rilevare che la discussione precedente mostra che, in circostanze date, non si ammette in generale una descrizione obiettiva se non approssimata; in conseguenza, non si può sfuggire al dogmatismo se si isola l'enunciato scientifico da un contesto evolutivo: infatti una descrizione non può essere pensata senza arbitrarietà come obiettiva e approssimata insieme, se non è anche pensata come provvisoria. Ciò corrobora il punto di vista di Popper (v., 1959; tr. it., p. 98) sul carattere provvisoriamente dogmatico delle asserzioni base della scienza empirica, da lui proposto come soluzione del ‛trilemma di Fries'.

Abbiamo detto che il valore preciso di una grandezza può essere definito idealmente tramite un certo processo di limite, purché la grandezza sia essa stessa ben definita. Nell'esempio discusso, i tratti segnati sulla sbarra potrebbero non essere esattamente paralleli, i bordi interni essere sbavati, ecc. In questo caso, neanche idealmente alla distanza in questione potrebbe essere attribuito un valore preciso: tale distanza sarebbe essenzialmente mal definita.

Vogliamo discutere un esempio meno banale e più istruttivo tratto dalla termodinamica statistica non quantica. Consideriamo precisamente il concetto di temperatura. Possiamo parlare di temperatura di un dato corpo nell'intervallo di tempo tra t e t + Δt con Δt a piacere, solo se questo ha un grandissimo numero di gradi di libertà, al limite un numero infinito, ed è in equilibrio termico con un bagno di calore avente un numero di gradi di libertà enormemente maggiore. In nessun caso reale, quindi, la temperatura è mai ‛esattamente definita' in un dato istante. Possiamo, è vero, se vogliamo, definire la temperatura anche per un sistema con un solo grado di libertà, per esempio un oscillatore armonico lineare, se rinunceremo però a precisare contemporaneamente il tempo. Supponiamo infatti di porre il nostro oscillatore armonico in un bagno di calore all'equilibrio termico a temperatura T e di assicurare un ‛buon contatto termico' tra oscillatore e bagno di calore, ossia di assicurarci che il teorema ergodico sia applicabile. Supponiamo di misurare la coordinata q ed il momento p dell'oscillatore senza disturbarlo, ciò che è classicamente possibile, in un grandissimo numero di diversi intervalli di tempo Δt_i. Troveremo che la distribuzione, nello spazio delle fasi dell'oscillatore, dei punti che avremo determinato sperimentalmente approssimerà quanto vogliamo la distribuzione canonica di Boltzmann, pur di prendere il numero di intervalli Δt_i e ΣΔt_i sufficientemente grande. Più semplicemente, l'energia media dell'oscillatore, mediata nel tempo, sarà uguale a kT con una precisione grande a piacere. L'oscillatore può quindi essere un termometro che ci dà correttamente la temperatura del bagno di calore, e quindi possiamo estendere la nozione di temperatura e parlare di ‛temperatura dell'oscillatore' purché la misura duri un tempo lunghissimo. Si deve quindi lasciare il tempo ‛indefinito' nel senso che non si può in nessun modo parlare di ‛temperatura dell'oscillatore' in un dato istante: tale temperatura non è semplicemente mal nota; essa è a sua volta totalmente indefinita. Abbiamo qui un esempio classico che mostra un'analogia molto stretta, e forse piuttosto illuminante, con la ‛complementarità quantica'.

Si noti che possiamo avere delle situazioni, diciamo così, intermedie: per esempio misurare l'energia media dell'oscillatore in n diversi intervalli di tempo uguali t, con t grande, ma non grandissimo, ottenendo diversi valori E₁,..., E_n fluttuanti intorno a kT. Se n è abbastanza grande, la media degli E_i approssimerà quanto si vuole kT, e l'espressione

potrà assumersi come misura della ‛indefinizione' (non dell'errore) della temperatura dell'oscillatore in ciascuno degli intervalli t.

Si può così stabilire un limite di ‛indefinizione' di una grandezza approssimativamente misurabile ma non esattamente definita in certe condizioni. È chiaro che non ha senso cercare di ridurre l'errore di misura al di sotto del limite di indefinizione.

b) Concetto di ‛obiettività classica' e principio di complementarità

Benché la ‛tesi ristretta dell'empirismo', quale era sostenuta tempo addietro dai cosidetti ‛fisicalisti', sia oggi quanto meno soggetta ad ampia revisione (v. Hempel, 1952; tr. it., p. 30 ss.; v. Popper, 1959; tr. it., p. 87 ss.), nessuno pone in dubbio il carattere empirico della fisica, o per lo meno il fatto che le teorie fisiche debbano condurre a risultati empiricamente controllabili; soltanto si insiste sul carattere ‛intersoggettivo' del controllo (v. Popper, ibid.), ossia si insiste sul carattere obiettivo secondo Poincaré, o se si vuole secondo Kant, come sin qui noi l'abbiamo definito.

Il fatto che, d'altra parte, nella fisica si debba necessariamente parlare, per esempio, di eventi non effettivamente osservati, senza poterli mettere su un piano epistemologico diverso da eventi effettivamente osservati, è indubitabile. Si consideri il caso della linea oraria di un pianeta, per esempio di Marte. Tale linea oraria è una linea continua nello spazio-tempo. Tuttavia, certo, non è osservata nè è osservabile come tale. Ciò che è osservato è un insieme di ‛punti' (eventi), ossia di quadruple di coordinate spazio-temporali, definiti solo convenzionalmente, in quanto osservati con certi errori.

La linea oraria si ottiene con una certa approssimazione mediante la meccanica celeste, utilizzando come dati iniziali alcuni degli eventi effettivamente osservati, insieme, naturalmente, ad altri analoghi eventi osservati sugli altri pianeti del sistema solare. Tale linea oraria passa ‛entro gli errori' per i ‛punti osservati'. Ogni ‛punto' della linea oraria così determinato per via teorica si deve considerare, fino a prova contraria, altrettanto genuino e definito con lo stesso errore, ossia con lo stesso grado di arbitrarietà, dei punti effettivamente osservati.

Un tale procedimento di interpolazione ed estrapolazione è fondato essenzialmente su un'ipotesi generale di ‛uniformità' della natura, ossia sull'ipotesi dell'esistenza di invarianze, e in particolare di ‛continuità', ed è essenziale per iniziare la costruzione della fisica. La questione è già stata discussa da molti autori, per esempio da Poincaré (v., 1903, pp. 34-35 e pp. 169 55., e 1904, pp. 258-259), e a questi rimandiamo.

Vogliamo qui fare solo due osservazioni particolari. La prima è che dalle argomentazioni dell'autore citato si rileva che, per la costruzione di una fisica grossolanamente macroscopica, ossia di una fisica di fenomeni rilevabili con i ‛nudi' sensi dell'uomo e tutt'al più con l'ausilio degli strumenti più semplici ed elementari (righelli graduati, fili inestensibili, traguardi, ecc.), l'ipotesi della continuità è metodologicamente necessaria. Ciò spiega le difficoltà concettuali che comporta l'introduzione della costante h nella fisica, come abbiamo già rilevato nel cap. 3, È c.

La seconda osservazione ci porterà a caratterizzare, in modo forse istruttivo, una differenza tra fisica classica e fisica quantica, che dal punto di vista metodologico è probabilmente essenziale.

Supponiamo, a tal proposito, che un astronomo determini la posizione P₀ di Marte al tempo t₀, e poi la posizione Ä al tempo õ. Il risultato che egli troverà, per esempio al tempo õ, è indipendente dal fatto che altri m astronomi abbiano fatto, all'insaputa o meno del primo astronomo, altre n osservazioni di posizioni ai tempi t₁,..., t_n, compresi tra t₀ e õ con i risultati P₁,..., P_n. Naturalmente si troverà che P₀, P₁,..., P_n, Ä staranno entro gli errori sull'orbita calcolata.

Giungiamo così alla definizione: se, dato un insieme Ô qualunque di osservazioni O₁, O₂,..., O_n eseguibili su un sistema o isolato, o sottoposto ad azioni esterne esattamente note, il risultato R_l di qualsiasi osservazione O_l∈Ô è indipendente dal fatto che le osservazioni appartenenti a qualsiasi sottoinsieme di Ô siano state effettivamente eseguite, diremo che l'insieme Ô è obiettivo C (C sta per ‛classicamente'). Si intende che R_l deve essere indipendente dal fatto che le altre osservazioni siano state eseguite, ma non dai risultati che tali osservazioni hanno avuto, o avrebbero avuto se eseguite.

Per esempio, qualunque insieme di osservazioni di posizione e velocità di un pianeta è obiettivo C.

Si comprende così come i punti della traiettoria di un pianeta, non effettivamente osservati, si possano porre sullo stesso piano conoscitivo di quelli osservati, e la traiettoria possa descriversi classicamente in se stessa senza alcun riferimento esplicito alle osservazioni. È infatti irrilevante che certe osservazioni siano state eseguite o no - e in questo consiste l'essere obiettivo C - ancorché per determinare la traiettoria sia necessario eseguire alcune osservazioni, magari non sulla traiettoria stessa, ma sugli altri pianeti del sistema solare. Possiamo così immediatamente estendere la nostra nozione di obiettivo C definita inizialmente come proprietà di un insieme di possibili osservazioni su di un sistema riferendola ai risultati ‛virtuali' di un insieme infinito di ‛virtuali osservazioni', e alla descrizione dello stato del sistema che ne deriva, e dire così che il sistema e il suo stato sono descritti in modo obiettivo C.

Così possiamo dire che la traiettoria e il moto di Marte sono obiettivi C. Solo se si vorrà discutere in modo concreto la precisione con cui la traiettoria è determinata, sarà necessario fare esplicito riferimento alle osservazioni che sono state effettivamente eseguite e al loro grado di approssimazione.

Se nella descrizione del sistema entrano grandezze che non hanno sempre un valore ben definito, come per esempio nella termodinamica, allora la descrizione può essere ancora obiettiva C ma solo entro certe non superabili approssimazioni, dipendenti inoltre caso per caso dallo stato del sistema.

Nella fisica classica, tuttavia, si era implicitamente supposto che valessero certe ipotesi che cercheremo di esplicitare qui di seguito. Ci limiteremo per semplicità al caso di sistemi isolati con un numero finito f di gradi di libertà, descrivibili canonicamente.

Prima ipotesi: per ogni q e per ogni p del sistema è definibile idealmente una successione di operazioni di misura M_q(n), M_p(n) con errori decrescenti aventi un limite M_q(∞), M_p(∞), con errore nullo; seconda ipotesi: M_q(∞) ed M_p(∞) sono tali che qualunque insieme di misure eseguite su qualunque insieme di p e q con i processi ideali limiti M_p(∞), M_q(∞) è obiettivo C.

La prima ipotesi implica che ciascuna q e ciascuna p è definibile in modo operativo ideale in maniera da avere valore esatto se misurata isolatamente. La seconda ipotesi implica che le p e le q sono misurabili esattamente tutte insieme.

Così nella fisica classica, benché si debba ammettere che una descrizione macroscopica di un sistema possa essere obiettiva C solo se si tollerano certe approssimazioni, si pensa che esista sempre una descrizione microscopica ideale dello stato di qualunque sistema che sia obiettiva C senza limitazioni e perfettamente esatta; questa sarebbe la ‛vera' esauriente descrizione dello stato del sistema, ed essendo obiettiva C senza limitazioni non necessiterebbe di alcun riferimento a operazioni di osservazione; basterebbe l'ipotesi implicita che tali ‛osservazioni ideali' siano possibili.

Alcuni filosofi della scienza sostengono che questa è una condizione necessaria a priori da imporsi a qualunque descrizione scientifica della natura (v., per es., Bunge, 1967).

Nella fisica quantica, la seconda ipotesi non vale.

In generale, anzi, non vale l'ipotesi che un insieme di osservazioni possa essere obiettivo C, salvo che in casi molto particolari, per esempio nel caso che si tratti di osservazioni relative ad osservabili rappresentate da operatori tutti commutabili tra di loro.

Richiamiamo l'esempio del cap. 3, È c, cioè l'esperienza di interferenza con l'interferometro di Michelson.

Supponiamo che l'osservatore A si disponga ad osservare l'effetto della radiazione sulla lastra fotografica. Ciò che egli osserverà dipenderà interamente dal fatto che un osservatore B abbia deciso di determinare, e determinato nel frattempo, con esattezza, la posizione del separatore d'onda, rispetto al resto dell'apparato, o la sua quantità di moto. Nel primo caso, A osserverà delle frange, nel secondo caso, osserverà un annerimento pressoché uniforme (s'intende, si tratta di esperimento ideale!).

Per questa ragione, una teoria quantica completa dovrebbe, almeno in via di principio, includere una definizione anche operativa delle osservabili. In ogni caso in una teoria quantica non si può prescindere dalla problematica relativa alla cosiddetta ‛teoria della misura'.

Già Bohr ha posto chiaramente in rilievo che ogni misura quantica su un sistema S comporta un'interazione tra S e un apparato di misura A comprendente una parte A_c il cui comportamento deve potersi descrivere classicamente.

Ma una descrizione classica deve essere una descrizione obiettiva C e quindi, data l'esistenza e finitezza di h, una descrizione necessariamente approssimata. E quale deve essere questa approssimazione? Ogni sottoinsieme dei gradi di libertà di A_c comprendente f_i gradi di libertà deve essere descritto, nel sottospazio delle fasi relativo, con una incertezza molto maggiore di h^fi; questa è veramente una condizione necessaria. Se gli stati quantici rilevanti sono assegnabili mediante opportuni insiemi di numeri interi, una condizione spesso sufficiente è che tutti i numeri quantici n_i che interverrebbero nella descrizione dello stato di A_c debbano essere grandi rispetto all'unità e i loro scarti quadratici medi dell'ordine di √-n-_i.

Una tale incertezza deve da una parte rendere possibile una descrizione obiettiva C, entro l'incertezza ammessa, e d'altra parte rendere impossibile l'osservazione di fenomeni di ‛interferenza quantica' (non di interferenza classica, come quelle che si possono osservare, per esempio, con le onde hertziane!) relativi alla parte A_c dell'apparato di misura.

Naturalmente vi è una certa indeterminatezza nella ‛individuazione' di A_c in A. I criteri precedenti, però, dovrebbero mostrare che tale indeterminatezza, in ogni caso concretamente definito, è assai meno lata di quanto generalmente si creda.

Per questo è utile ricordare che cambiare la precisione con cui un osservabile o un insieme di osservabili deve essere misurato può significare, e in generale quando la precisione diventi dell'ordine dell'indefinizione quantica di fatto significa, un cambiamento radicale di esperimento, e precisamente il passaggio da un esperimento a un altro complementare nel senso di Bohr.

La presunta larghezza della zona indefinita in cui collocare la barriera tra ‛parte quantica' e ‛parte classica' dell'apparato di misura in diversi casi proviene dal fatto che, anche se ciò non è sempre esplicitamente chiaro, si stanno in realtà considerando esperimenti differenti.

Tre ultime osservazioni. Si è detto da molti che il principio di complementarità di Bohr ‛non ha valore predittivo'.

Si è anche detto che il carattere indeterministico della fisica quantica debba essere provvisorio, e il carattere deterministico della fisica potrebbe essere ristabilito con l'introduzione di ‛variabili nascoste' (come ai tempi dell'etere cosmico).

Si sostiene anche che la fisica deve dare una descrizione ‛obiettiva' del mondo. Generalmente il senso di obiettivo non è però ben specificato. Non si tratta qui di obiettività nel senso di Poincaré, perché anche la fisica quantica è obiettiva in quel senso. Si potrebbe forse pensare che si voglia dire che la descrizione deve essere obiettiva C nel senso che ho cercato di definire, e pertanto non riferirsi esplicitamente in modo necessario ad osservazioni (questo è infatti quello che è generalmente richiesto). Bene. Il principio di complementarità di Bohr predice che il mondo è fatto in modo tale che non se ne può dare una descrizione obiettiva C con precisione che superi l'indefinizione imposta da h. Come tale, è coerentemente un principio: proibisce qualcosa e potrebbe essere smentito dall'esperienza, mostrando sperimentalmente che si può dare una descrizione obiettiva C con precisione maggiore a quella consentita da h.

Seconda osservazione. Si è detto che la fisica quantica ha permesso forse il più grande progresso, da quando la scienza moderna è sorta, verso una visione unitaria del mondo empirico, esaltando il ‛ruolo esplicativo' della fisica nelle varie discipline che si occupano della natura.

Tuttavia se si accetta il punto di vista essenzialmente indeterminista della fisica quantica, l'autonomia delle varie discipline della storia naturale è chiaramente stabilita. I fatti singoli di cui si possono predire solo probabilità di accadimento possono diventare non meno decisivi delle invarianze della fisica nel determinare il corso di fenomeni importantissimi come l'evoluzione della vita; così necessità e caso hanno ognuno la loro parte, e quale sia stata la parte del caso effettivamente verificatasi possono dirlo solo le scienze che si occupano della storia della natura. Un discorso a parte meriterebbe la cosmologia; ma è troppo arduo per essere svolto in breve e lo tralasceremo.

Terza osservazione. Reichenbach ha suggerito l'idea che il carattere indeterministico della meccanica quantica dovrebbe imporre l'uso di una logica a più di due valori (Reichenbach, 1949). Ciò non sembra strettamente necessario e nemmeno opportuno, almeno se ci si riferisce alla formulazione convenzionale della meccanica quantica come sembra faccia Reichenbach. Potrebbe forse divenire, se non necessario, opportuno, alla luce di un teorema di Araki e Yanase, secondo il quale anche nella misura di una osservabile a due valori soli, salvo casi eccezionali, vi sarebbe sempre una probabilità diversa da zero di ottenere un risultato non corrispondente a nessuno dei due valori. Una simile eventualità, d'altra parte, è presa indipendentemente in esplicita considerazione in recenti tentativi di ‛teorie realistiche' di misura quantica, tenendo conto della inevitabilità dei veri e propri errori di misura, oltre che della indefinizione quantica (v. Giles, 1970).

c) L'esperimento e la genesi delle teorie; il ‛dilemma del teorico'

La fisica è una scienza empirica. Non certo però nel senso dei vecchi ‛empiristi'.

Penso, in ciò pienamente d'accordo con Popper (v. 1959; tr. it., pp. 6-7), che la classica obiezione di Hume contro la possibilità di fondare la scienza su un principio di ‛induzione empirica' sia insormontabile. Rimando a Popper (ibid.) per la discussione dell'argomento.

Concordo poi con l'asserzione di Einstein, contenuta in una lettera a Popper, e su questo punto d'accordo con il ricevente (ibid., p. 520), che ‟la teoria non possa essere fabbricata a partire dai risultati dell'osservazione, ma possa solo essere inventata" (del resto, una tale asserzione è in linea con la filosofia della scienza di Einstein, come può essere inferito da numerosi altri suoi scritti).

L'idea così espressa deve essere accettata, però, con importanti qualificazioni.

È chiaro intanto che la fisica non è una scienza a priori nel senso di Kant e nemmeno di Eddington, ma su ciò Einstein e Popper sarebbero pienamente d'accordo. Non è nemmeno, in senso stretto, una libera creazione dell'intelletto umano, ancorché nella formulazione di ogni teoria veramente nuova debba intervenire un libero atto inventivo. Questa libertà, però, non è totale arbitrio e l'invenzione non è una creazione dal nulla.

Basterebbe l'analisi del formarsi storico della scienza a mostrano; diceva, ben giustamente, un gigante come Newton che egli aveva potuto vedere più lontano di quelli venuti prima di lui, giust'appunto perché posto sulle spalle dei ‛giganti che l'avevano preceduto'.

Consideriamo, per esempio, il caso della scoperta della teoria della relatività ristretta. È quanto meno dubbio che Einstein fosse informato in modo abbastanza esauriente sulla situazione sperimentale relativa al fallimento dei tentativi di rivelare il ‛vento d'etere'. Tuttavia egli conosceva certamente le equazioni di Maxwell e la teoria di Lorentz. Entrambi, Maxwell e Lorentz, sono stati influenzati, e particolarmente Maxwell, dai risultati e dal pensiero di Faraday. Ora, Faraday è stato uomo di idee genialissime, di immaginazione ricchissima di inventiva, ma sarebbe assai difficile negare, almeno per Faraday, che questa immaginazione inventiva lavorava in virtù di una essenziale ‛interazione' tra mente e natura per il tramite dell'esperimento. Quindi le equazioni di Maxwell e la teoria di Lorentz non avrebbero potuto prendere origine senza il contributo ineliminabile di un pensiero nutrito dall'esperienza.

D'altra parte, in che cosa consiste l'atto di ‛libera invenzione' di Einstein nel caso della relatività ristretta? Non nel fatto di ammettere valevole per l'elettromagnetismo il principio della relatività: ciò era già stato ammesso da Poincaré, per esempio, e implicitamente anche da Lorentz. Solo che Lorentz cercava di giustificare tale principio sulla base di considerazioni ancora prerelativistiche.

Il contributo geniale di Einstein alla ‛invenzione della relatività' è stato un atto di ‛libera decisione' di cambiare la prospettiva di base prendendo sul serio, in modo fondamentale, il principio di relatività ristretta per l'elettromagnetismo e di costruire su questo l'edificio della teoria dello spazio-tempo della meccanica e naturalmente dell'elettromagnetismo stesso.

È simile l'atteggiamento mentale di Bohr, Kramers e Slater nella ‛invenzione' della loro teoria del 1924, la quale, benché non fosse corretta, conteneva importanti elementi della successiva formulazione della meccanica quantica. Lo descrivo con le parole di Heisenberg (v., 1955, p. 12): ‟Nel 1924 Bohr, Kramers e Slater asserirono, prima di tutto, che la programmazione delle onde di luce, da una parte, e il loro assorbimento e la loro emissione in quanti, dall'altra, sono fatti sperimentali che devono essere posti alla base di ogni tentativo di chiarificazione e non liquidati con una semplice spiegazione; le conseguenze fondamentali di questo stato di cose devono perciò essere prese sul serio

Anche qui si tratta di una ‛libera decisione' concernente il punto di prospettiva fondamentale sotto cui un certo stato di cose doveva essere considerato; ma è chiaro che questa ‛libera decisione' era basata su una profonda conoscenza, oltre che di teorie precedenti come la termodinamica statistica, di fatti empirici che, appunto, venivano considerati fondamentali in virtù della decisione stessa.

Dunque si può ripetere che la libera creazione teorica non è una creazione dal nulla.

Anzi, il contributo dell'‛esperimento' non è semplicemente indispensabile da un punto di vista pratico, ma qualcosa di più: non è infatti solo maieutica o solo discriminante di alternative. Di un singolo esperimento o gruppo di esperimenti si può forse dire che hanno avuto una funzione maieutica, di altri che hanno avuto una funzione discriminante, ma l'effetto complessivo di tutti i validi esperimenti nello sviluppo del pensiero scientifico è qualcosa che trascende completamente tutto questo e va molto al di là di quanto mente umana, senza questo essenziale gioco di interazione con la natura che è l'esperimento, avrebbe mai potuto concepire o anche immaginare a priori.

Del resto, per convincersi della correttezza di questo punto di vista, è probabilmente istruttivo seguire lo svolgimento dei lavori e i risultati delle ricerche, molte delle quali estremamente serie e pregevoli, volte ad indagare la possibile struttura di teorie quantum-relativistiche o meccanico-statistiche consistenti, prescindendo da un accordo con i fatti di questo mondo, ossia senza nessuna pretesa che si tratti di vere e proprie teorie fisiche, ma accontentandosi di ricerche ‛di laboratorio fisico-matematico', come si dice in gergo. Ebbene, nel quadro quantum-relativistico, dopo notevolissimi sforzi, si è riusciti fino ad ora a ‛realizzare' un mondo costituito da un gas reale con atomi (nel senso etimologico) debolmente interagenti in sole due dimensioni spaziali. Un mondo un po' povero rispetto all'estrema ricchezza di quello in cui viviamo. Si sottolinea che ciò non è detto per nulla come critica di queste ricerche (che anzi sono tra le più serie ricerche teoriche, in vista della situazione di cui si è brevemente scritto nel cap. 3, È d), ma serve ad illustrare ancora una volta quanto siano essenziali i dati empirici introdotti ‛a mano' nelle teorie, anche senza sapere se con tale procedimento non si arriverà a gravi inconsistenze.

Difesa così la parte dell'‛esperimento', ci si può domandare se è altrettanto difendibile quella della ‛teoria'.

Gli empiristi stretti hanno posto in dubbio l'indispensabilità della teoria nella descrizione scientifica del mondo. Secondo tale tesi, l'unico scopo legittimo di una teoria è di stabilire, di solito tramite un certo formalismo matematico, che implica una catena di passaggi, correlazioni tra fenomeni osservabili. Se è così, perché non fare semplicemente un elenco di tali ‛correlazioni' fra ‛antecedenti' e ‛conseguenti' osservabili, eliminando tutto il resto? (v. Hempel, 1952, tr. it., pp. 114 ss.; v. Hull, 1943, p. 284; v. Skinner, 1953, p. 352). La difficoltà è presentata sotto il nome del ‛dilemma del teorico'.

Naturalmente ci sono diverse dotte confutazioni del ‛dilemma del teorico', non tutte perfettamente convincenti. Io mi limiterò ad osservare che, al tempo in cui furono scoperte le equazioni di Maxwell, sarebbe stato impossibile compilare la più gran parte, in ogni caso quella più caratteristica e interessante, dell'‛elenco' sostitutivo della teoria, semplicemente perché non si conoscevano né mezzi per produrre, nè mezzi per rivelare le onde hertziane.

Obiezioni del tipo di quella del ‛dilemma del teorico', benché talvolta provenienti da tutt'altri quartieri, si fondano in ultima analisi su una dimenticanza: ci si dimentica che, procedendo nel tentativo di descrivere coerentemente il mondo dell'esperienza, la scienza lo allarga, talvolta, in modo mirabile e quasi incomprensibile per i ‛non addetti ai lavori' (per i quali tali allargamenti passerebbero per lo più inosservati se non fosse per le ‛ricadute tecnologiche').

È d'altra parte proprio per questa capacità predittiva ed euristica della teoria, che il problema del valore conoscitivo della scienza non può essere ignorato o risolto in modo totalmente negativo. Di ciò si è ben reso conto, per esempio, Croce, il quale, per mantenere la sua nota posizione epistemologica nei riguardi della scienza, nega il potere predittivo della teoria (egli dice della ‛legge') semplicemente tentando di ridicolizzarlo. Lo cito alla lettera, sia pure omettendo alcune parole o periodi. ‟Si osserva allora che [...] il vero fine delle scienze naturali non è la classe, ma la legge, e che nella legge il rigore di verità è indubitabile tanto che per mezzo delle leggi che si sono scoperte è possibile, niente meno, formare previsioni di quel che sarà per accadere. Miracoloso potere, in vero, che metterebbe le scienze naturali al di sopra ad ogni altra forma di conoscenza, anzi le doterebbe di forza quasi magica [...] e il naturalista sarebbe in questo caso nè più nè meno che lo scientifico e metodico erede degli antichi veggenti. Basterebbe la miracolosità del vantato potere a far dubitare che la legge innalzi davvero le scienze naturali a scienze di verità" (v. Croce, 1909, p. 199).

Duole dire che questo tentativo di ridicolizzazione è vanificato dai fatti, in particolare dai fatti della storia della scienza, come chiunque ne conosca qualcosa potrà facilmente riconoscere.

d) Questioni di valore

Chiuderemo questo articolo discutendo, sia pure in modo del tutto inadeguato, alcune questioni relative al ‛valore della fisica', tanto più che questioni del genere interessano la scienza naturale nel suo insieme, data la parte che ha la fisica tra le varie discipline che studiano la natura.

Credo che sia già chiaro che punto importante e forse determinante della nostra discussione sia un approfondimento di quanto già ho cominciato a dire sulla funzione e sul valore della teoria nella descrizione del mondo empirico. Innanzitutto respingo una concezione puramente pragmatista della scienza. Per questo basterebbe forse rimandare a Platone (Teeteto, 172 a-b), utile a ricordarsi in questi tempi di esami di coscienza della civiltà tecnologica, o in modo più specifico a Poincaré (v., 1904, pp. 218 ss.).

Con questo è respinta anche una concezione interamente ‛convenzionalista' della scienza. Ma anche la concezione ‛convenzionalista' della ‛teoria' o dei ‛principi' mi sembra inaccettabile. Le ragioni sono più o meno quelle esposte da vari autori a cui rimando (v., per es., Reichenbach, 1928; v. Popper, 1959, tr. it., pp. 67 ss.).

Così anche non mi soffermerò sulle filosofie che limitano il valore della teoria al fatto che la teoria farebbe ‛economizzare pensiero' nella descrizione degli eventi naturali, un po' per le stesse ragioni per cui ritengo inaccettabili le concezioni ‛pragmatiste' e convenzionaliste', e poi perché è assai dubbio che in realtà la teoria faccia molto spesso economizzare pensiero. In linea di principio io potrei usare la meccanica quantistica per calcolare le frequenze e le intensità di tutte le righe emesse nel visibile e nell'ultravioletto, per esempio dall'alluminio, ma, se mi occorre saperle, preferisco di gran lunga guardare tabelle dove sono riportati risultati sperimentali in proposito. Nonostante questo, sono convinto che è molto importante che, ripeto, in linea di principio, siano calcolabili a partire da una teoria generale. Considerazioni di questo tipo, approfondite, fanno sorgere riserve anche sul criterio di valutazione di Popper, fondato sul ‛grado di controllabilità' delle teorie (v. Popper, 1959; tr. it., pp. 107 ss.), almeno se dovesse essere inteso come unico e meccanico criterio di giudizio.

Per illustrare queste riserve, userò l'esame di un caso particolare, e, precisamente, della teoria di Sommerfeld della struttura fine spettroscopica dell'idrogeno.

È noto che Sommerfeld, usando appunto le condizioni di Bohr-Sommerfeld della vecchia formulazione della teoria dei quanti, e tenendo conto anche della meccanica relativistica, senza aggiungere alcuna ipotesi ad hoc, derivò un'espressione per la struttura fine dell'idrogeno confermata in modo straordinario dai risultati sperimentali.

Purtroppo si dovette successivamente concludere che tale accordo tra teoria ed esperienza era casuale, perché fu scoperto che l'elettrone ha un momento magnetico intrinseco e, introducendo tale momento in una teoria alla Sommerfeld, si perde l'accordo con l'esperienza.

Ora, almeno applicando meccanicamente i criteri alla Popper, mi sembra si dovrebbe concludere che la teoria di Sommerfeld era superiore a quella primitiva di Bohr.

E tuttavia, giudicando con un altro criterio, che mi pare dovrebbe quanto meno integrare i criteri di Popper, si arriva alla opposta conclusione; Sommerfeld aveva fatto la ‛scelta sfortunata' di prendere troppo sul serio la vecchia formulazione della teoria dei quanti, che conteneva importanti elementi di verità, ma era ancora troppo rozza e inconsistente. Ciò naturalmente non è inteso affatto come un rilievo critico nei riguardi di Sommerfeld, di cui si può dire solo che la fortuna fu troppo inadeguata ai meriti altissimi. Si noti, tra l'altro, che la struttura fine dell'idrogeno è veramente un effetto relativistico, e in ciò Sommerfeld aveva visto perfettamente giusto. Inoltre, probabilmente, a suo tempo, tentativi come quello di Sommerfeld dovevano essere fatti, giusto per saggiare la portata della vecchia teoria dei quanti.

E tuttavia bisogna ripetere che fu un tentativo sfortunato. Ma come possiamo dirlo ora? Giusto con il ‛senno del poi', ossia con un criterio di giudizio storico.

Ci si può domandare quanto è valido un tale criterio di giudizio a posteriori. Occorre tener presente, innanzitutto, che un criterio non meramente tecnico di giudizio sulla scienza non può essere che metascientifico e che, mentre la scienza può predire nuovi accadimenti naturali, non vi è filosofia della scienza che possa predire senza dogmatismo come sarà la scienza del futuro e nemmeno porre delle condizioni a priori che limitino il suo sviluppo, se non forse le più late condizioni di consistenza e di obiettività alla Poincaré. Anche queste condizioni possono essere diversamente intese lungo il corso della storia, per le nuove esigenze che si pongono di mano in mano che la scienza evolve. (Questo stesso fatto rimanda ai posteri un giudizio sufficientemente preciso sulla scienza di oggi).

È istruttivo vedere come un tale criterio storico funziona su esempi concreti.

Consideriamo il caso del ‛principio dell'equipartizione dell'energia'. All'epoca in cui fu scoperto, era fondato sull'ipotesi atomica meccanicista e sulla statistica classica (a cui pochi, in realtà, credevano) e aveva avuto un certo numero di conferme e un numero comparabile di insuccessi, tutti relativi a predizioni sui calori specifici.

Poi servì ad ispirare i lavori di Perrin e ne uscì fortemente corroborato, portando però al sorgere di una situazione paradossale, come abbiamo spiegato. Non sarebbe stato necessario essere dei puristi per denunciare l'inconsistenza di tutto il procedimento impiegato per la ‛dimostrazione sperimentale' dell'esistenza degli atomi. E tuttavia vera inconsistenza non c'era, ma ciò poteva essere chiarito solo con la teoria quantica: il principio dell'equipartizione dell'energia è valido per certi gradi di libertà, diciamo q_c, quando i livelli energetici possono, con buona approssimazione, essere spezzati in somme di termini, ciascuno dei quali sia associabile a certi gradi di libertà; tra, questi debbono esserci quelli descritti dalle q_c e, inoltre, i termini consecutivi associati alle q_c debbono differire tra di loro per molto meno di kT. Non vale in caso contrario. Tutto ciò si può vedere facilmente facendo uso della legge canonica di Boltzmann (v. sopra, cap. 2, È c), da cui lo stesso principio classico di equipartizione dell'energia era stato derivato.

Così la fisica quantica non elimina il principio di equipartizione, ma lo fa meglio comprendere, determinandone i limiti di approssimata validità. Inutile ricordare che in tal modo risulta acclarato che Perrin aveva fatto uso legittimo del principio di equipartizione, che nella sua esperienza gli atomi si debbono comportare come se fossero tali nel senso etimologico della parola, e ogni inconsistenza o petizione di principio scompare.

Consideriamo invece l'ipotesi delle ‛masse magnetiche'. Benché si usi tuttora, a scopi pratici, per il calcolo del campo generato da magneti, essa non entra più nella struttura fondamentale della fisica e, a meno che non si scopra il ‛monopolo di Dirac', è molto probabile che non vi entrerà più in avvenire.

Era sembrato, nel secolo passato, che lo stesso dovesse accadere per il concetto di carica elettrica: invece esso vi è rientrato per starci a pieno diritto, con la scoperta dell'elettrone e della carica elementare.

Ma trattiamo l'ultimo esempio ancor più semplice e probabilmente più profondo. Abbiamo detto nell'introduzione che la descrizione del mondo empirico è fondata sul riconoscimento di certe invarianze, sia pure approssimate. Ora le prime invarianze che sono state riconosciute scientificamente sono quelle che danno origine al gruppo dei movimenti euclidei; così è stata scoperta la geometria, così si è giunti ai primi risultati scientifici validi riguardanti l'astronomia. Ora, indubbiamente, in tale scoperta hanno avuto un'importanza fondamentale quelle proprietà dei corpi solidi che noi, più o meno propriamente, possiamo chiamare geometriche. Queste proprietà, che solo tramite la quantizzazione oggi possiamo fisicamente giustificare, riducendole a caso particolare della ‛stabilità' della materia, hanno avuto un'importanza continua, ineliminabile, e in certo senso preminente, in tutto lo sviluppo della scienza. Hanno dato luogo al sorgere della geometria, che, se da una parte si è sviluppata come scienza svincolata dalle basi empiriche, dall'altra è servita come mezzo indispensabile per il formarsi e il progredire della fisica e delle altre scienze della natura. D'altra parte, da un punto di vista operativo, si può osservare che non c'è praticamente strumento di misura in cui le proprietà di ‛invarianza geometrica' dei solidi non entrino in qualche modo essenziale. Non è azzardato dire che, senza ‛solidi', la scienza che noi conosciamo non avrebbe potuto sorgere.

Così tutti questi esempi, e molti altri che si potrebbero addurre, mostrano che i concetti, le ipotesi, le teorie che sono state proposte e usate nel corso della storia della scienza cadono in due classi piuttosto nettamente distinguibili. Alcuni, come gli epicicli e i deferenti dell'astronomia tolemaica, il flogisto, probabilmente le masse magnetiche, l'etere cosmico, ecc., sono sorti e caduti senza lasciare alcuna traccia fondamentale nello sviluppo successivo della scienza. Essi a suo tempo servirono a molti degli scopi estrinseci che si attribuiscono alle teorie (come classificare, descrivere in modo semplice i fenomeni empirici, ecc.), ma sembra che vadano considerati come veri accidenti, i quali potrebbero benissimo essere dimenticati. Altri concetti, ipotesi, ecc., come le proprietà geometriche dei solidi, la descrizione copernicana del sistema solare, la meccanica classica, la stessa ipotesi atomica, ecc., una volta stabiliti sembrano possedere la proprietà di permanere nel patrimonio della scienza che pur si evolve. Non si intende che essi permangono inalterati una volta scoperti, ché, anzi, in generale subiscono limitazioni e reinterpretazioni; ma essi sono riconoscibili in qualche modo anche nelle nuove più avanzate teorie che li hanno superati, o, anzi, debbono essere addirittura supposti come una prima approssimazione, valevole in certi casi almeno, perché le nuove teorie possano essere criticamente fondate (per es., i concetti della meccanica statistica classica per fondare criticamente la fisica quantica), e mostrano così di avere una parte essenziale e non accidentale nell'evolversi della scienza.

Naturalmente, la distinzione in queste due classi può essere soggetta a revisione nel corso della storia della scienza; ma ci sono casi che sembrano chiari al di fuori di ogni ragionevole dubbio. Certo non v'ha certezza assoluta, come si deve riconoscere, se si prende sul serio l'argomento di Hume contro l'induzione empirica e si rifiuta ogni dogmatismo.

Occorre dunque fare una certa ‛scommessa'; rifiutarsi a questa scommessa, o peggio ‛scommettere contro' la fondatezza della possibilità della distinzione (non di una particolare classificazione) non mi sembrerebbe molto ragionevole. Equivarrebbe a pensare seriamente che tutte le odierne teorie potrebbero ridursi un giorno allo stato di quella del flogisto. Questo è quello che sembra pensare Kuhn (v., 1962), al quale però, mi pare, è sfuggita, o è parsa irrilevante, la distinzione che si è cercato di porre in rilievo.

Ma se la distinzione è fondata, allora mi pare difficile negare che sia importante e forse decisiva. Essa sembra implicare che la scienza si evolve in un processo di tipo progressivo non meramente descritto dal numero dei fatti empirici in accordo con le teorie, ma implicante un progresso ‛formale'; se si ricorda, cioè, quanto detto a proposito della funzione dell'esperimento nella scienza e si è d'accordo, pare che si possa pensare che le ‛buone' teorie ci dicono con verità, sul mondo, qualcosa di più di quanto dicono i meri fatti empirici, e questo qualcosa è di natura strutturale, cioè formale.

Se è così, in questo forse consiste l'appropriato punto di partenza per tentare di comprendere sia l'intrinseco valore della scienza sia l'istintivo ‛realismo ingenuo' del fisico che, a dispetto di ogni tentativo di critica, continua ad ispirare il lavoro della maggior parte degli scienziati (v., per es., Planck, 1933; tr. it., pp. 217-241).

bibliografia

Araki, H., Yanase, M., Measurements of quantum mechanical operators, in ‟Physical review", 1960, CXX, pp. 622-626.

Bohr, N., On the constitution of atoms and molecules, New York 1965.

Boltzmann, L., Vorlesungen über Gastheorie, I parte, Leipzig 1896, II parte, Leipzig 1898.

Bunge, M., Foundations of physics, Berlin 1967.

Carnap, R., Philosophical foundations of physics, New York 1966 (tr. it.: I fondamenti filosofici della fisica, Milano 1971).

Croce, B., Logica come scienza del concetto puro, Bari 1909.

Eddington, A., Thephilosophy of physical science, Cambridge 1939 (tr. it.: La filosofia della scienza fisica, Bari 1941).

Einstein, A., The meaning of relativity, London 1922, Princeton 1945² (tr. it.: Il significato della relatività, Torino 1953).

Fermi, E., Molecole e cristalli, Bologna 1934.

Gibbs, J. W., Elementary principles in statistical mechanics developed with special reference to the rational foundation of thermodynamics, New Haven 1914.

Giles, R., Foundations for quantum mechanics, in ‟Journal of mathematical physics", 1970, XI, pp. 2139-2160.

Heisenberg, W., Die physikalischen Prinzipien der Quantum Theorie, Leipzig 1930 (tr. it.: I principi fisici della teoria dei quanti, Roma 1948, Torino 1953², 1963³).

Heisenberg, W., Wandlungen in den Grundlagen der Naturwissenschaft, Leipzig 1935 (tr. it.: Mutamenti nelle basi della scienza, Torino 1944, 1960²).

Heisenberg, W., The development of the interpretation of the quantum theory, in Niels Bohr and the development of physics, London 1955, pp. 12-29.

Hempel, C. G., Fundamentals of concept formation in empirical science, in Intertnational encyclopedia of unified science, vol. II, 7, Chicago 1952 (tr. it.: La formazione dei concetti e delle teorie della scienza empirica, Milano 1961).

Hull, C. L. T., The problem of intervening variables in moral behaviour theory, in ‟Psychological review, 1943, L, pp. 271-291.

Khinchin, A. I., Mathematical foundations of statistical mechanics, New York 1949.

Kuhn, Th., Structure of scientific revolutions, Chicago 1962 (tr. it.: La struttura delle rivoluzioni scientifiche, Torino 1969).

Lorentz, H. A., Einstein, A., Minkowski, M., Das Relativitätsprinzip. Eine Sammlung von Abhandlungen, Leipzig 1920.

Millikan, R. A., The electron, Chicago 1927.

Monod, J., Le hasard et la nécessité. Essai sur la philosophie naturelle de la biologie moderne, Paris 1970 (tr. it.: Il caso e la necessità. Saggio sulla filosofia naturale della biologia contemporanea, Milano 1972⁵).

Pauli, W., Relativitätstheorie, Leipzig 1921 (tr. it.: La teoria della relatività, Torino 1958).

Pauli, W., Die allgemeinen Prinzipien der Wellenmechanik, Ann Arbor, Mich., 1947.

Pauli, W., Exclusion principle, Lorentz grup and space-time reflection, in Niels Bohr and the development of physics, London 1955, pp. 30-51.

Perrin, J., Les atomes, Paris 1913.

Planck, M., Vorlesungen über die Theorie der Wärmestrahlung, Leipzig 1921.

Planck, M., Wege zur physikalischen Erkenntnis, Leipzig 1933 (tr. it.: La conoscenza del mondo fisico, Torino 1942²).

Poincaré, H., Electricité et optique, Paris 1901.

Poincaré, H., La science et l'hypothèse, Paris 1903 (tr. it.: La scienza e l'ipotesi, Firenze 1949, 1950²; nuova ed. Roma 1963).

Poincaré, H., La valeur de la science, Paris 1904 (tr. it.: Il valore della scienza, Firenze 1947, 1952²).

Popper, K. R., The logic of scientific discovery, London 1959 (tr. it.: Logica della scoperta scientifica, Torino 1970).

Reichenbach, H., Philosophie der Raum-Zeit-Lehre, Berlin 1928.

Reichenbach, H., Philosophische Grundlage der Quantenmechanik, Basel 1949 (tr. it.: I fondamenti filosofici della meccanica quantistica, Torino 1964).

Segrè, E., Nuclei e particelle, Bologna 1966.

Skinner, B. F., Science and human behaviour, New York 1953.

Whittaker, E. T., History of the theories of aether and electricity, London 1910.

Whittaker, E. T., A treatise on the analytical dynamics of particles and rigid bodies, Cambridge 1937⁴.