Fisica
Fisica
(XV, p. 473; App. II, i, p. 950; III, i, p. 619; IV, i, p. 812; V, ii, p. 246)
Gli argomenti riguardanti la f. sono stati svolti ampiamente, sia nell'Enciclopedia Italiana sia nelle successive Appendici, nelle voci specifiche: dalle voci fisica atomica (App. IV, i, p.817) e acustica, riprese anche in questa Appendice, alle voci dinamica molecolare (App. V, i, p.832), quark (App. V, iv, p.371), suono (App. V, v, p.334), e così via. Una trattazione specifica è stata anche dedicata ai dispositivi sperimentali, agli strumenti di osservazione e di misurazione e simili, quali contatore (App. IV, i, p. 520), laser (App. V, iii, p.137) ecc. Le voci intitolate espressamente alla f. hanno avuto pertanto il ruolo di voci quadro, entro cui sono state esposte le teorie, o i sistemi di teorie, funzionali e complementari agli articoli specifici. Così, nel vol. XV si delinea l'evoluzione storica delle conoscenze fisiche fino ad allora acquisite; nell'App. II vengono presentati quei filoni di ricerca avanzata che intorno agli anni Quaranta si erano ormai consolidati, come la meccanica quantistica, la f. delle particelle e la f. nucleare. Nella voce dell'App. III si affronta la f.dei fondamenti nella transizione dalla f. classica alla f. moderna, focalizzando l'attenzione sui principi di relatività, sull'ipotesi di quantizzazione dell'energia, sulla nascita della meccanica ondulatoria e delle matrici, e si delinea il complesso quadro in cui si stava articolando la f., dalla f. delle alte energie, alla f. dei fluidi e dei plasmi, fino alla geofisica e all'astrofisica; sono ripresi nell'App. IV i principi che hanno segnato il passaggio alla f.moderna, soffermandosi sui fenomeni macro- e microscopici, sul principio di causalità e di indeterminazione; nell'App. V, infine, si ritorna al filone storiografico, con riguardo allo sviluppo degli studi di storia della f., di particolare rilievo nei tempi recenti. La voce che segue, ancorché formalmente dedicata a che a prima vista potrebbe apparire strumentale e accessorio, quali sono i calcolatori elettronici, concerne in realtà un aspetto, e non di carattere secondario, dell'attuale f. teorica per le molte applicazioni, tuttora in fase di studio. *
Calcolatori nella fisica teorica
di Enzo Marinari
Il grande sviluppo dei calcolatori elettronici degli ultimi decenni ha reso possibile la nascita di nuovi settori di ricerca in cui si utilizzano proficuamente la potenza di calcolo dei supercalcolatori e le tecniche matematiche avanzate della f. teorica. In tal modo sono nate idee nuove che hanno ampliato il panorama degli interessi della f. teorica moderna il cui sviluppo è affidato a derivazioni euristiche, spesso spregiudicate, affiancate da calcoli di tipo numerico e simbolico effettuati dal calcolatore. La mancanza di un completo rigore matematico nelle prime fasi dello sviluppo è accettato al fine di accelerare il progresso delle idee, mentre il necessario rigore matematico spesso si ottiene in un momento successivo. I calcolatori sono quindi potenti strumenti di lavoro, come gli acceleratori di particelle lo sono per la f. sperimentale delle particelle elementari; il loro ruolo è diventato così importante che i fisici teorici, oltre a utilizzare i supercalcolatori commerciali, che sono progettati per uso generale, preferiscono sempre più definire i loro strumenti di calcolo modellandoli in base alle esigenze specifiche della problematica affrontata. Accade inoltre che questa nuova attività influenzi il modo stesso di pensare, guidando a volte la scelta delle direzioni in cui si muoverà la ricerca futura.
Gli elaboratori dedicati sono concepiti sulla base della tecnologia d'avanguardia disponibile al momento del progetto, spesso affiancata da innovazioni tecnologiche nei processori e nell'hardware di comunicazione. Anche il software presenta soluzioni innovative, in modo tale che molti calcolatori dedicati sono in grado di affrontare problemi anche molto lontani da quelli tipici della materia iniziale di studio.
L'uso del calcolatore elettronico è essenziale in tutti i campi della f., particolarmente in quei casi in cui si affrontano problematiche nelle quali giocano un ruolo fondamentale più scale di lunghezze o di tempi. In effetti si sa prevedere con relativa facilità il comportamento dei sistemi in cui una sola scala di lunghezza determina la soluzione (per studiare la caduta di un'arancia dall'albero non è necessario conoscere le equazioni che determinano il comportamento dei suoi elettroni), mentre s'incontrano gravi difficoltà nella descrizione del comportamento macroscopico di un sistema la cui dinamica dipenda da un gran numero di scale di lunghezze differenti. È questo, per es., il caso dello studio dei fenomeni critici e della turbolenza dei fluidi, anche quando viene utilizzato il potente strumento teorico del gruppo di rinormalizzazione.
La teoria che più ha richiesto l'impiego di calcolatori dedicati è indubbiamente la cromodinamica quantistica (QCD; v. cromodinamica quantistica, App. V), la teoria fondamentale delle interazioni forti. La QCD, che è una teoria di campo relativistica ed è formulata in termini di equazioni nel continuo spazio-temporale della relatività ristretta e della meccanica quantistica, può essere discretizzata sostituendo il continuo spazio-temporale con un reticolo di punti in quattro dimensioni e riscrivendo le sue equazioni differenziali in equazioni alle differenze finite sul reticolo. In tal modo la QCD reticolare è automaticamente formulata nella forma ideale per poter essere direttamente elaborata numericamente dal calcolatore. Naturalmente si pone il problema non banale di ritradurre i risultati ottenuti nel limite del continuo, nel limite cioè in cui il reticolo viene infittito sempre più e la sua spaziatura tende a zero.
Nel caso della QCD reticolare, come nei problemi tipici di modelli di spin che aiutano a indagare la struttura della materia (v. probabilità, calcolo delle: Campi stocastici discreti, App. V), le equazioni sono definite su una griglia equispaziata, e le operazioni necessarie a risolvere il problema sono locali, in quanto un sito del reticolo ha bisogno solo di informazione proveniente dai siti vicini e da se stesso: queste caratteristiche sono cruciali nell'ottimizzare il progetto di calcolatori dedicati. Per es., la QCD reticolare è diventata recentemente, anche e soprattutto grazie ai calcolatori dedicati, un vero strumento fenomenologico, che consente di fornire previsioni fisiche a partire dai principi primi.
Si propone di seguito una schematica rassegna di alcuni degli insegnamenti principali, acquisiti dalle esperienze fatte recentemente, che probabilmente influenzeranno in qualche misura nel futuro l'arte di progettare i calcolatori dedicati alla f. teorica.
1) Mantenere il maggior livello di semplicità possibile. Pagare un piccolo aumento di efficienza o un miglioramento poco rilevante con una grande complessità aggiuntiva è un cattivo investimento. Questo vale, per es., per la rete di comunicazione e per la struttura del processore aritmetico.
2) Mantenere il giusto livello di flessibilità. Cercare una flessibilità eccessiva per un problema che non la richiede vuol dire correre il rischio di ricadere nell'errore del punto precedente.
3) Avere un sistema di software di buona qualità. Tutti i calcolatori dedicati che sono riusciti a diventare utili per un mercato più generale avevano un sistema di software di alto livello di programmazione.
4) Per quel che riguarda l'architettura, tenere conto che la gestione da parte del compilatore delle memorie indirizzabili veloci (register files) del processore aritmetico generalmente rende l'elaboratore molto efficiente.
5) Considerare che la costruzione di processori deputati a svolgere funzioni particolari, come per es. il processore aritmetico e quello di comunicazione, è fattibile e utile. Questi tipi di processori sono spesso di tipo VLIW (Very Long Instruction Word), cioè dotati di molte possibili istruzioni di microcodice lunghe e dettagliate, il che implica lo svolgimento di molte azioni in parallelo. Questa concezione è opposta a quella RISC (Reduced Instruction Set Computer, processore con un insieme ridotto di istruzioni), dove sono disponibili poche istruzioni specifiche e un'operazione complessa usa molte istruzioni (v. elaboratori elettronici, in questa Appendice).
6) Non trascurare l'esistenza di una nicchia di mercato per i calcolatori nati principalmente per gli studi in f. teorica.
Tecnologia
Le caratteristiche principali dei calcolatori dedicati alla f. teorica sono il reticolo equispaziato, la località della domanda di calcolo, la possibilità di usare più volte un dato del problema, una volta caricato nelle memorie veloci del processore aritmetico. Molto spesso queste impostazioni hanno permesso agli elaboratori concepiti per gli studi di f. teorica di essere utilizzabili con successo anche in altri ambiti, e molte soluzioni progettuali escogitate per i calcolatori dedicati hanno poi trovato applicazione anche in alcuni supercalcolatori paralleli commerciali. I calcolatori dedicati alla f. teorica hanno un'architettura tipicamente SIMD (Single Instruction Multiple Data), o direttamente per concezione hardware o, come nel caso di calcolatori potenzialmente MIMD (Multiple Instruction Multiple Data), per il software che vi è stato sviluppato e per il tipo di uso che se ne è fatto. Gli elaboratori paralleli di tipo SIMD, in cui tutti i processori eseguono la stessa istruzione ma trattano dati diversi, sono ottimali per trattare problemi definiti su un reticolo regolare e omogeneo (a ogni processore viene assegnata una parte dello spazio fisico), ma hanno anche uno spettro di possibili utilizzazioni di alta efficienza molto più vasto di quanto spesso si pensi: uno sforzo nello studio di algoritmi efficaci (che sono spesso meno banali di quelli, forse più intuitivi, destinati a un calcolatore MIMD) è ricompensato da un'architettura più semplice ed economica, e da un software che è ottimizzabile molto più semplicemente.
I problemi tipici che hanno visto il successo di architetture SIMD e l'applicabilità di elaboratori nati per lo studio della f. teorica sono, per es., il controllo del traffico aereo, l'analisi di dati radar, lo studio di fluidi (per es. per applicazioni petrolifere), la meteorologia. Il costo è stato, ovviamente, una delle considerazioni principali che ha spinto verso la costruzione di calcolatori dedicati: nel 1989 un supercalcolatore Cray offriva prestazioni di un megaflops (10⁶ flops, ossia operazioni tra numeri razionali al secondo) per 10.000 dollari, mentre i processori Weitek, usati in talune macchine dedicate alla f. teorica della prima generazione, avevano un prezzo di circa 25 dollari per megaflops. L'ultimo calcolatore dedicato concepito al dipartimento di Fisica della Columbia University ha un costo di circa 3 dollari per megaflops.
Le prime macchine SIMD, come il DAP (Distributed Array Processor) e il MasPar (Massively Parallel), possono essere considerate antenati diretti dei calcolatori che descriveremo qui. Macchine commerciali di uso solo parzialmente generale, come la Meiko Computing Surface e la Connection Machine, sono invece dei cugini vicini. È indubbio che i calcolatori sviluppati nell'ambito degli studi in f. teorica abbiano avuto un ruolo propulsivo nel campo delle applicazioni di architetture parallele.
I calcolatori dedicati italiani: la serie APE
Il progetto di calcolatori ottimizzati per la f. teorica, APE (originariamente sigla di Array Processor with Emulator, e in seguito di Array Processor Experiment), è iniziato nel 1984 da sforzi dei fisici italiani dell'Istituto nazionale di fisica nucleare (INFN). Il progetto è finalizzato allo studio della cromodinamica quantistica e della f. delle interazioni fondamentali, ma l'approccio innovativo con cui è stato realizzato ha alla fine reso APE un calcolatore efficacissimo per lo studio di una vasta tipologia di problemi comprendenti, per es., la fluidodinamica e la meteorologia; per questo motivo si è rivelato addirittura un calcolatore commerciale di notevole successo. Si tratta di un elaboratore concepito secondo l'idea base di essere realmente SIMD (anche se nell'ultima versione è stato aggiunto dell'hardware destinato a rendere possibile una certa dose di operatività MIMD), dotato sin dall'inizio di un linguaggio evoluto veramente parallelo.
La storia di APE si articola in tre momenti. Il primo calcolatore della serie, APE-1, anche se è stato prodotto in una decina di esemplari di varie grandezze e potenze di calcolo, non ha mai raggiunto un livello di elevata ingegnerizzazione. La versione completa della macchina era dotata di 16 nodi (ognuno comprendente 4 moltiplicatori e 4 addizionatori Weitek, e un gruppo di 128 register files), per una velocità di punta di un gigaflops e un'efficienza fino al 90% per programmi perfettamente ottimizzati (nel caso di APE, tutte le efficienze indicate si riferiscono a programmi scritti interamente in linguaggio di alto livello, senza l'uso di linguaggio macchina o di scrittura diretta di codice a basso livello), e con una semplice topologia ad anello. Una sola scheda, detta emulatore, nata nei laboratori del CERN (Conseil Européen pour la Recherche Nucléaire) di Ginevra, effettuava il controllo del programma di tutte le schede (compresa la trasmissione degli indirizzi delle locazioni di memoria accessibile, che erano uguali per tutte le schede seguendo le regole dell'architettura SIMD). Una delle considerazioni principali su cui era basata l'architettura di APE era che la vera proprietà limitativa dei calcolatori basati su processori veloci (sostanzialmente tutti i calcolatori prodotti oggi) è la banda passante disponibile per le comunicazioni tra processore e memoria veloce. Qui APE era aiutata dalle particolari caratteristiche delle equazioni della cromodinamica quantistica, che sono basate su matrici 333 complesse (matrici del gruppo SU(3)). Tipicamente in questo caso, una volta portati 40 operandi alla memoria veloce (register files), è possibile utilizzarli per circa 200 operazioni aritmetiche. Questo fattore 5 è cruciale per consentire prestazioni eccezionali con efficienza vicina al 90%. Altri problemi, in cui la banda passante necessaria è maggiore, finiscono comunque per avere una buona efficienza, che, per es., è vicina al 25% nel caso dei problemi tipici di meccanica statistica.
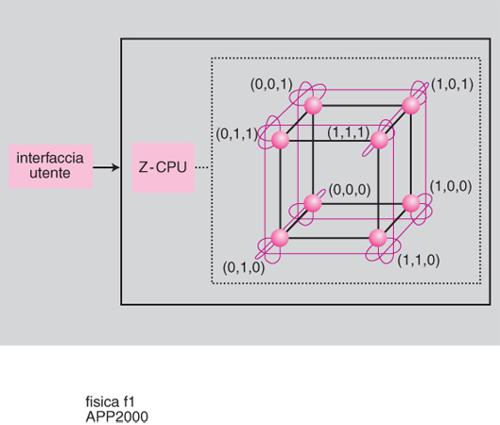
APE-100 è stata invece una macchina che ha raggiunto un alto livello di ingegnerizzazione: la sua produzione in serie, gestita dall'industria italiana Alenia, ha riscosso un notevole successo commerciale con un'alta percentuale di modelli esportati, soprattutto in Germania e in Francia. L'altra grande novità di APE-100 è stato un uso intenso del VLSI: in questo caso, sia il processore aritmetico sia quello di comunicazione sono stati progettati dai fisici autori del progetto. Il processore chiamato MAD (Multiply and Add Device), cuore di APE-100, è stato il primo processore aritmetico di grande potenza prodotto in Europa. APE-100 raggiunge, nella sua versione più potente, una velocità teorica di 100 gigaflops (sempre con un'efficienza molto elevata per problemi regolari ad alta intensità di calcolo). Una scheda contiene 8 processori e può costituire la versione più piccola di APE-100, detta cubo, con una velocità teorica di 400 megaflops: 16 schede in un opportuno contenitore (crate) costituiscono una configurazione intermedia della macchina detta tubo, mentre una torre (con una velocità teorica di 25 gigaflops) è costituita da 4 crate. La topologia è quella di un cubo tridimensionale con condizioni periodiche ai bordi. Nella fig. 1 è mostrato uno schema di APE-100, con l'interfaccia utente, il controllore (detto Z-CPU) e 8 processori.
APEmille, l'ultima versione della serie APE, è in questo momento in fase di ultimazione, e raggiungerà una velocità teorica di un teraflops (10¹² flops). La rete di connessione è semplice, una griglia tridimensionale periodica, e si tratta ancora di un elaboratore del tipo SIMD (anche se più flessibile dei modelli precedenti: qui è permesso un indirizzamento locale della memoria). L'aritmetica è in singola precisione con la possibilità di un'emulazione software della doppia precisione che non rallenta drasticamente le prestazioni, e l'unità di calcolo contiene un grande register file. Le prestazioni teoriche sono di circa 0,5 gigaflops per processore (con un'efficienza che si spinge a 0,8 per i casi di maggior interesse). Una scheda composta da 8 nodi aritmetici, uno di controllo e uno di comunicazione, ha prestazioni di 4 gigaflops (10⁹ flops). Il linguaggio parallelo ad alto livello chiamato TAO consente una programmazione di alto livello molto efficiente. L'accesso ad APEmille è garantito da una rete di personal computer di tipo IBM gestiti dal sistema operativo Linux, connessi al nucleo del calcolatore da interfacce veloci basate sul bus PCI (Peripheral Component Interconnect). Un'importante caratteristica di APEmille consiste nell'essere divisibile via software in varie entità separate; in tal modo si potranno sviluppare contemporaneamente vari progetti di ricerca.
Rassegna dei calcolatori dedicati esteri
I primi processori dedicati alla f. teorica sono nati nel 1982, ed erano progettati per lo studio del più semplice modello di magnete, il modello di Ising. Qui viene introdotto un reticolo cubico, su ogni sito del quale è definita una variabile che può assumere i valori 11 e 21 e interagisce con i suoi primi vicini. Questo modello, così semplice, contiene tutta l'essenza dei fenomeni critici come la magnetizzazione spontanea di un materiale. Ovviamente la logica a due valori consente la realizzazione di un hardware specializzato particolarmente efficiente. Questi due processori (nati uno a Santa Barbara, in California, e l'altro a Delft, in Olanda) erano completamente dedicati al problema specifico che era codificato nell'hardware: non esisteva un vero programma e tutta la logica era contenuta nell'architettura hardware del calcolatore.
Il processore di Santa Barbara era basato su un'architettura particolarmente innovativa, che consentiva di trattare 25 milioni di spin al secondo: una memoria speciale consentiva al processore (che agiva su 16 bit elementari alla volta) di disporre delle variabili necessarie senza bisogno di alcun calcolo di indirizzi. Il generatore di numeri casuali era incluso nell'hardware e fu causa di vari problemi (è molto difficile avere un controllo soddisfacente del comportamento dei generatori di numeri pseudocasuali: in questo caso furono scoperte correlazioni fra i valori generati che potevano rendere inaccurato il risultato del calcolo); ciò ha costituito un primo insegnamento sul fatto che un hardware dedicato deve comunque avere un grado di flessibilità che consenta di adattarsi al fallimento di un algoritmo o alla scoperta di un algoritmo più potente. Il processore di Delft aveva invece un carattere estremamente più classico.
Due dei progetti di maggior impegno e di maggior successo del campo hanno avuto come teatro il dipartimento di Fisica della Columbia University a New York. La nota caratterizzante di questi progetti è stata probabilmente quella di puntare al miglior rapporto fra costo e prestazioni possibili: l'obiettivo fondamentale era quello di ottenere le migliori prestazioni possibili per il problema specifico della cromodinamica quantistica reticolare, minimizzando il costo dei componenti. Inoltre è stata fatta la scelta di non costruire strumenti software di ottimizzazione avanzati: in tutte le versioni, le procedure che svolgevano la gran parte del calcolo hanno dovuto essere codificate in linguaggio macchina. Questo punto di vista, da un lato, ha portato a una macchina di grande potenza e basso costo, ma, dall'altro, ha reso meno facile, forse, una diffusione anche commerciale della macchina (com'è avvenuto invece nel caso del calcolatore italiano APE e del calcolatore giapponese QCDPAX).
Due prototipi, formati rispettivamente di 16 e 64 nodi, costruiti fra il 1985 e il 1988, hanno preceduto la versione finale del primo calcolatore di Columbia, costituito da 256 nodi e completato nel 1990. Una velocità teorica di 16,4 gigaflops corrispondeva a una velocità reale (per un problema ottimale) di 6,4 gigaflops. Processori per il calcolo aritmetico da 64 bit Weitek erano accoppiati a delle memorie veloci indirizzabili (register files), seguendo un approccio introdotto da APE. La struttura delle connessioni fra i processori era una struttura toroidale periodica. È interessante notare che la macchina ha sempre funzionato in modo SIMD e che gli elementi MIMD hanno trovato un uso solo in momenti di messa a punto e controllo. Come per APE e per altri progetti, il numero di nodi era sostanzialmente contenuto. Citiamo fra i problemi studiati quello della transizione di deconfinamento dei quark, e il potenziale efficace per quark pesanti (v. cromodinamica quantistica, App. V). La seconda macchina di Columbia, detta QCD-DSP, spingendo agli estremi il criterio di minimo costo descritto prima, si è basata su un'idea particolarmente originale, riuscendo a raggiungere il risultato notevole di un costo finale di meno di 3 dollari per megaflops. I nuclei elementari della macchina sono stati basati su processori di elaborazione di segnali digitali DSP (Digital Signal Processing): infatti questi processori possono eseguire operazioni aritmetiche a un costo estremamente basso. Ancora una volta le funzioni principali sono state scritte in linguaggio macchina. I nuclei di calcolo DSP sono stati fatti comunicare mediante un processore dedicato alle comunicazioni, progettato dagli stessi fisici, il processore NGA. Una scheda contiene 64 nodi per una velocità teorica di 3,2 gigaflops. Le procedure di test sono state curate in gran dettaglio (così come per APE-100). La macchina raggiunge su codici ottimali un'efficienza compresa fra il 15 e il 30%, e lavora in precisione semplice (aritmetica a 32 bit). La versione più potente della macchina è in corso di installazione presso i Laboratori nazionali di Brookhaven (New York), e comprenderà 12.288 nodi per una velocità teorica di 614 gigaflops e una velocità effettiva massima compresa fra 100 e 200 gigaflops.
La realizzazione di GF11, un progetto ambizioso dell'IBM di Yorktown (New York), è stata rallentata da numerosi problemi di affidabilità dell'hardware, ma è stata finalmente condotta in porto. GF11 è risultato essere un calcolatore di grande potenza: i problemi incontrati costituiscono un'importante lezione sul grado di complessità da richiedere a progetti di questo tipo. In questo caso, il sistema di comunicazione dati previsto era molto flessibile e ambizioso (forse troppo per un calcolatore sostanzialmente dedicato allo studio di un problema locale, regolare e omogeneo): sembra chiara l'opportunità di ridurre le complicazioni hardware al minimo necessario per rendere l'architettura adatta ai problemi presi in esame. La versione finale di GF11 ha una velocità teorica di 11gigaflops, e su problemi ottimali ha prestazioni vicine ai 6 gigaflops reali. La memoria totale è di 1,1 gigabyte. Un controllore centrale gestisce la distribuzione del microcodice ai processori paralleli. La rete di connessione è non-locale, e può essere riconfigurata durante l'esecuzione del programma. Viene trasferita una parola di 32 bit ogni 200 nanosecondi.
Il calcolatore parallelo ACPMAPS (Advanced Computer Program Multiple Array Processor System), destinato allo studio della cromodinamica quantistica, è stato concepito e realizzato presso i laboratori Fermilab (Batavia, Illinois, USA). Probabilmente questo è stato il tentativo più spinto verso un approccio MIMD fra quelli qui descritti. È da notare anche un notevole sviluppo del software, che è culminato nel sistema CANOPY, un pacchetto di software destinato a una programmazione agevole ed efficiente di applicazioni su griglie reticolari. Una velocità massima di 5 gigaflops era in questo caso accompagnata da una memoria di 2 gigabyte.
È interessante citare l'Ipercubo di Caltech, che è stato uno dei precursori dei calcolatori dedicati a studi in f. teorica. Nato nell'ambito del gruppo di Fisica delle alte energie e del dipartimento di Computer Science di Caltech, in California, la sua destinazione è presto divenuta parzialmente commerciale, e la sua produzione è curata dalla Intel. Il modello originario (prodotto nel 1982) era formato da 64 processori organizzati in un ipercubo di dimensioni 2⁶ (che permetteva una corrispondenza diretta con un reticolo 4³), era basato sul processore Intel 8086/8087 e aveva prestazioni (notevoli per quel periodo) equivalenti a quelle di circa 10 VAX 780.
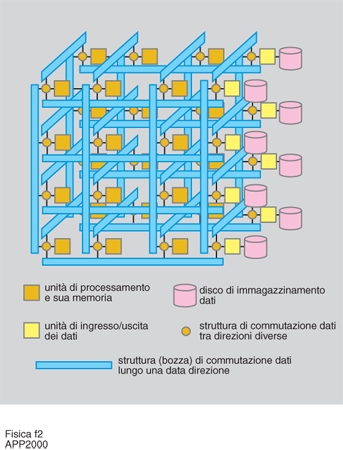
Il Giappone ha contribuito in modo notevole allo sviluppo dei calcolatori specializzati. La serie PAX (Parallel Array Experiment), sviluppata principalmente a Tsukuba, è culminata nella costruzione degli elaboratori QCDPAX e CP-PACS (Computational Physics by Parallel Array Computer System). QCDPAX, progettato nel 1987, è divenuto completamente operativo nel 1990. Realizzato a Tsukuba, è stato il quinto calcolatore della serie PAX. Composto in particolare da 480 processori connessi da una rete toroidale bidimensionale, QCDPAX era di natura MIMD (anche se il suo modo di utilizzazione tipico è sempre stato di tipo SIMD), con una velocità teorica di 14 gigaflops, ed efficienza di circa il 50% (fig. 2).
CP-PACS, progettato a partire dal 1992, è terminato nel 1997; è un elaboratore di grande potenza, composto da 2048 processori e capace di 614 gigaflops teorici. I processori MIMD (di tipo RISC) sono qui collegati in un reticolo tridimensionale. Il processore di calcolo, realizzato proprio per CP-PACS, è realizzato con tecnologia CMOS da 0,3 mm. CP-PACS occupa un'area di 7 m per 4,2 m, è raffreddato ad aria e utilizza un sistema operativo Unix. La costruzione è stata curata in gran parte dalla Hitachi, che raccoglieva e organizzava l'esperienza e le indicazioni accademiche, e che commercializza ora il calcolatore. CP-PACS è stata una grande impresa nazionale (nota interessante per un paese, come il Giappone, che non ha bisogno di recuperare, al contrario dell'Europa, un notevole margine di arretratezza in questo campo). Il Ministero per l'educazione, la scienza e la cultura giapponese ha dedicato a questo progetto ingenti finanziamenti. A Tsukuba è stato creato un Centro per la fisica computazionale, che ha coordinato gli studi connessi a CP-PACS ed è cresciuto in parallelo all'elaboratore.
bibliografia
A. Hoogland et al., A special-purpose processor for the Monte Carlo simulation of Ising spin system, in Journal of computational physics, 1983, 51, pp. 250-60.
R.B. Pearson et al., A fast processor for Monte Carlo simulation, in Journal of computational physics, 1983, 51, pp. 241-49.
E. Brooks et al., Pure Gauge SU(3) lattice theory on an array of computers, in Physical review letters, 1984, 52, pp. 2324-27.
P. Bacilieri et al., The APE computer, in Computing in high energy physics. Proceedings of the conference, Amsterdam 25-28 june 1985, Amsterdam-New York 1986, pp. 330-37.
N. Christ, QCD machines, in Nuclear physics B, 1989, 9, pp. 549-56.
M. Fischler et al., The FermiLab lattice supercomputer project, in Nuclear physics B, 1989, 9, pp. 571-75.
D. Weingarten, The status of GF11, in Nuclear physics B, 1990, 17, pp. 272-75.
C. Battista et al., APE 100, in International journal of high speed computing, 1993, 5, pp. 637-56.
Y. Iwasaki, The CP-PACS project, in Nuclear physics B, 1997, 53, pp. 1007-9.
R. Mawhinney, QCDSP, in Nuclear physics B, 1997, 53, pp. 1010-13.
R. Tripiccione, The APEmille parallel processor: an overview, in Multi-scale phenomena and their simulation (World scientific), Singapore 1997, pp. 91-99.