flesso

flesso

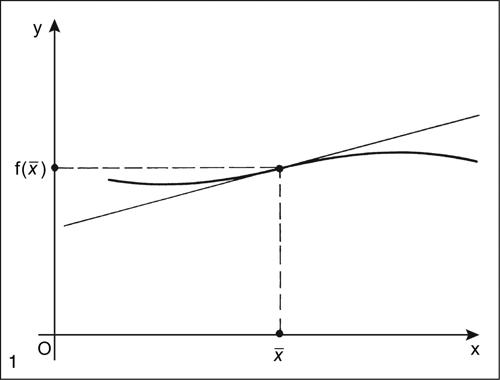
flesso punto interno al dominio di una funzione reale, in esso derivabile, in cui il grafico attraversa localmente la sua tangente. Più precisamente, un punto x̄ interno al dominio D di una funzione ƒ(x): D ⊆ R → R, derivabile in x̄, si dice punto di flesso se il grafico di ƒ attraversa localmente in x̄ la sua tangente, cioè se esiste un intorno U di x̄ tale che in U il segno della differenza ƒ(x) − [ƒ(x̄) + ƒ′(x̄)(x − x̄)] sia sempre concorde (flesso ascendente) o discorde (flesso discendente) con quello di (x − x̄).

Se ƒ ammette derivate fino all’ordine 2k + 1, k ≥ 1, affinché ƒ abbia un punto di flesso è sufficiente che ƒ″(x̄) si annulli assieme a tutte le derivate successive fino all’ordine 2k e sia ƒ^(2k+1)(x̄) ≠ 0, il caso più semplice essendo quello in cui ƒ⁽³⁾(x̄) ≠ 0. Il flesso è ascendente se tale derivata è positiva, discendente se negativa. Per esempio, le funzioni ƒ(x) = x^2k+1, k ≥ 1, ammettono un flesso ascendente nell’origine. Se invece la prima derivata non nulla è di ordine pari, il grafico della funzione non attraversa la sua tangente e ha concavità di verso costante.

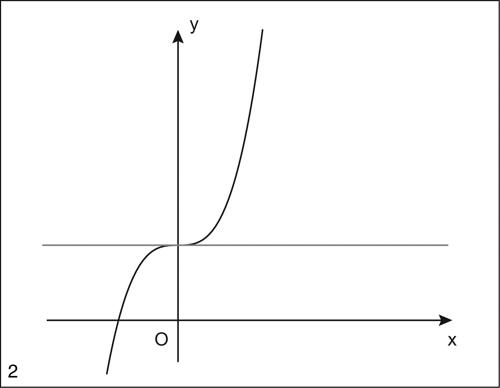
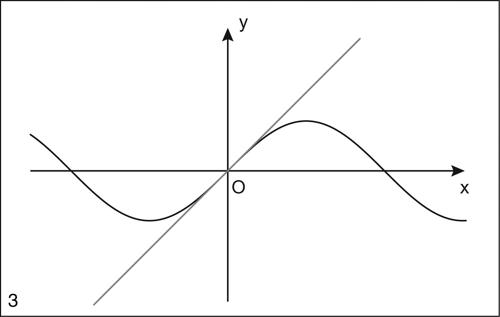
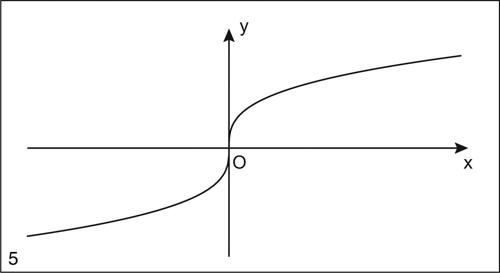
Va precisato che il valore della derivata prima, ƒ′(x̄), non ha alcuna importanza. Se tuttavia ƒ′(x̄) = 0, la tangente nel punto di flesso è orizzontale e conseguentemente il flesso è anch’esso detto orizzontale, mentre se ƒ′(x̄) ≠ 0, è detto obliquo. Per esempio la funzione y = sinx ha un flesso obliquo ascendente (la retta y = x) nell’origine. Invece la funzione y = 2x³ + 1 ha un flesso orizzontale di equazione y = 1 nel punto (0, 1) dove la funzione è crescente.

Il segno della derivata prima implica che la funzione sia crescente o decrescente, mentre il segno della derivata terza si traduce nell’essere il flesso ascendente o discendente. Solo per flessi orizzontali un flesso ascendente corrisponde a una funzione crescente e uno discendente a una funzione decrescente; negli altri casi le due nozioni sono indipendenti. La condizione sulla prima derivata non nulla non è necessaria, come mostrano sia le funzioni ƒ(x) = x^2k+1/3, k ≥ 1, sia ƒ(x) = |x|^2k−1x, che hanno tutte un flesso ascendente nell’origine senza essere derivabili 2k + 1 volte.

Lo stesso si dica della funzione

con ƒ(0) = 0; essa ha ancora un flesso nell’origine, ma tutte le sue derivate di ogni ordine si annullano per x = 0. In questi esempi la presenza del flesso si deduce dal cambiamento di segno della derivata di ordine 2k, che si annulla nell’origine. Anche questa condizione però è sufficiente ma non necessaria: la funzione y = x3 + x5[2 + cos(x−1)] ha il segno di x, quindi attraversa la sua tangente y = 0 nell’origine, dove ha un flesso ascendente. Tuttavia, in ogni intorno dell’origine, sia a destra che a sinistra, la sua derivata seconda cambia segno infinite volte.

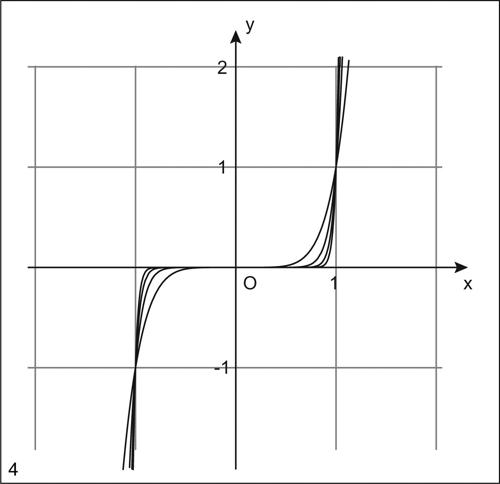
Se infine una funzione ƒ(x) è continua ma non derivabile in x̄, dove ha tangente parallela all’asse y, si parla di flesso verticale se si ha cambiamento di concavità, deducibile dal segno in un intorno di x̄ della derivata seconda, necessariamente non definita in x̄. Per esempio, la funzione y = x1/3 ha nell’origine un flesso verticale.