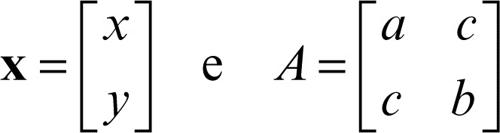forma bilineare simmetrica, forma quadratica di una

forma bilineare simmetrica, forma quadratica di una

forma bilineare simmetrica, forma quadratica di una in algebra lineare, per una → forma bilineare simmetrica ƒ su uno spazio vettoriale V definito su un campo K che, per semplicità si può considerare coincidente con R, è l’applicazione q: V → R che a ogni vettore v ∈ V associa q(v) = ƒ(v, v) = v^TAv, essendo A la matrice quadrata a coefficienti in R i cui elementi sono le immagini tramite ƒ dei versori del riferimento. Se si considera una generica forma quadratica in due variabili in scrittura polinomiale, quale ax² + by² + 2cxy, questa può essere riscritta come q(x) = x^TAx, essendo