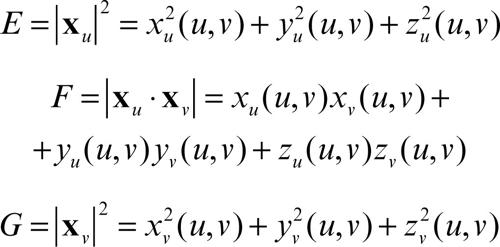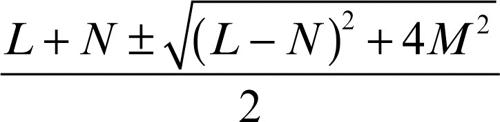forme quadratiche fondamentali
forme quadratiche fondamentali
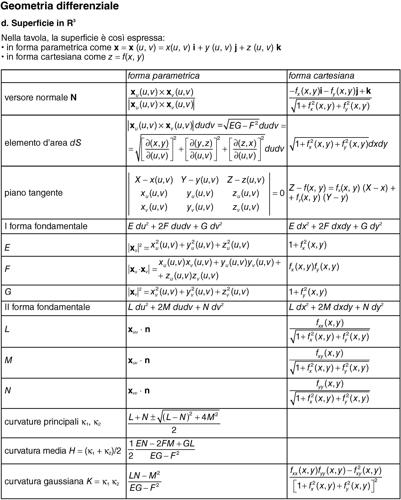
forme quadratiche fondamentali in geometria differenziale, due espressioni quadratiche nei differenziali che caratterizzano una superficie a meno di un’isometria. Si indichi con ds2 il generico elemento d’arco sulla superficie tra un punto x = x(u, ν) = x(u, ν)i + y(u, ν)j + z(u, ν)k e uno a esso infinitamente vicino. La prima forma fondamentale è (in forma parametrica):
dove E, F, G sono rispettivamente:
La seconda forma fondamentale è:
con L = xuu ⋅ n, M = xuv ⋅ n, N = xvv ⋅ n dove n è il versore normale. Dalla seconda forma fondamentale si ricavano le curvature principali della superficie, k1 e k2, attraverso la loro espressione:
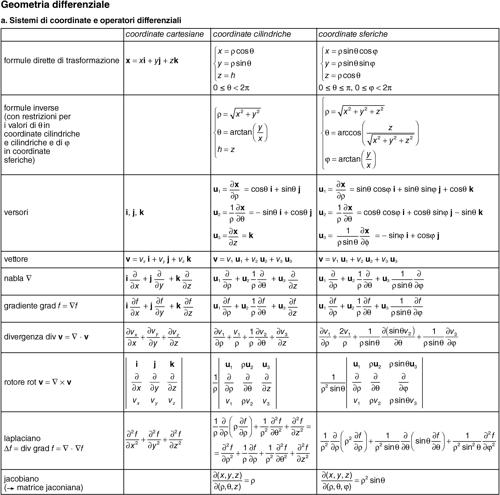
Le due forme fondamentali permettono di determinare la curvatura media e la curvatura di Gauss o totale (si vedano le tavole delle formule di geometria differenziale).
