formula decidibile
formula decidibile
formula decidibile in un calcolo logico, formula ben formata a tale che o essa stessa o la sua negazione ¬a (si legge «non a») siano dimostrabili formalmente in tale calcolo. Ciò equivale a dire che a è decidibile se è un teorema (cioè è dimostrabile nel calcolo) oppure è un teorema la sua negazione (¬a). Per esempio, la formula A ∨ ¬A (si legge «A o non A») e la formula A ∧ ¬A (si legge «A e non A») del linguaggio degli enunciati sono entrambe decidibili. La prima formula esprime infatti il principio del terzo escluso ed è dimostrabile formalmente secondo le regole del linguaggio degli enunciati; la seconda, invece, è una contraddizione ed è sempre falsa, pertanto è possibile dimostrare la sua negazione, cioè la formula ¬(A ∧ ¬A) che, per le leggi di → De Morgan, è equivalente alla prima formula.
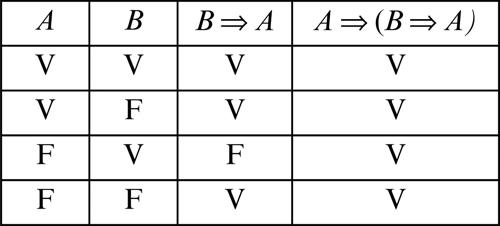
Un esempio di formula non decidibile fu costruito da Gödel per dimostrare l’incompletezza sintattica dell’aritmetica formalizzata da un sistema di assiomi (→ Gödel, teorema di). Lo scopo della dimostrazione ideata da Gödel è quello di mostrare che esiste una formula a, scritta nel linguaggio dell’aritmetica, tale che né a stessa né la sua negazione ¬a siano dimostrabili all’interno dell’aritmetica stessa. La decidibilità di una formula comporta la possibilità di definire una funzione calcolabile ƒ che assume un certo valore, per esempio 1, se l’espressione rappresentata dalla formula è vera, e un altro valore, per esempio 0, se è falsa. Per questo motivo il problema della decidibilità è strettamente collegato al problema della calcolabilità di una funzione. Se una formula è decidibile allora è possibile definire una procedura algoritmica che permetta di stabilire, in un numero finito di passi, se tale formula è dimostrabile oppure se è dimostrabile la sua negazione. Un esempio di procedura siffatta è fornito, nel calcolo degli enunciati, dalle tavole di verità. Per esempio, alla formula A ⇒ (B ⇒ A) (si legge «A implica B implica A»), scritta nel linguaggio degli enunciati, corrisponde la seguente tavola di verità:
Dalla tabella precedente si evince che la formula A ⇒ (B ⇒ A) è una tautologia, cioè risulta sempre vera (valore di verità V) in corrispondenza di ogni valore di verità delle lettere che la compongono. È noto, grazie al teorema di deduzione, che ogni tautologia è dimostrabile nel calcolo degli enunciati; pertanto la formula A ⇒ (B ⇒ A) è dimostrabile.
Un calcolo logico come il calcolo degli enunciati, in cui esiste una procedura in grado di individuare tutte le formule decidibili, viene detto calcolo decidibile. Occorre tuttavia chiarire che, in un calcolo decidibile, non tutte le formule sono necessariamente decidibili; basta considerare, nel calcolo degli enunciati, le lettere enunciative, che rappresentano gli enunciati atomici, le quali possono essere vere o false a seconda del valore di verità che si attribuisce loro.