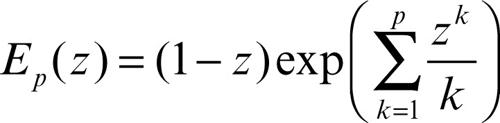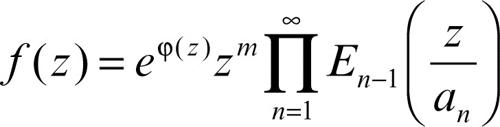Weierstrass, formula di
Weierstrass, formula di
Weierstrass, formula di in analisi, esprime mediante un prodotto infinito una qualsiasi funzione trascendente intera avente come zeri gli elementi di una successione {an} di numeri complessi, il cui unico punto di accumulazione sia il punto all’infinito. Il problema di determinare una funzione trascendente intera che si annulli in una assegnata successione {an} di punti del piano complesso, avente come unico punto di accumulazione il punto all’infinito, ammette infinite soluzioni. Si noti che se i punti {an} avessero un punto di accumulazione al finito, la trascendente intera sarebbe identicamente nulla, per il secondo principio di identità delle → funzioni analitiche.
Queste soluzioni sono definite a meno di un fattore che non si annulla mai e che ha la forma eφ(z), con φ trascendente intera arbitraria. Sia m ≥ 0 l’ordine di molteplicità dell’eventuale zero posto nell’origine e si supponga dunque che gli an siano diversi da 0 e ordinati per modulo crescente (a parità di modulo, si possono ordinare per argomento crescente, ma è irrilevante). Se uno zero ha molteplicità p, lo si ripete p volte nella successione.
Si definisca il cosiddetto fattore primo (o primario) di Weierstrass Ep(z) mediante la formula
con E0(z) = (1 − z). Le funzioni cercate sono allora date dalla seguente formula (di Weierstrass):
