Fotonica

Fotonica

Il termine fotone nasce per descrivere la minima quantità di energia E=hν (dove h=6,62606876±52×10⁻³⁴ Js è la costante di Planck) che un campo elettromagnetico oscillante a frequenza ν può trasportare, in accordo con la descrizione luce-materia data dalle leggi della meccanica quantistica. Il termine fotonica viene coniato nei Bell Laboratories (Stati Uniti), successivamente all'invenzione del laser nel 1960 ‒ in analogia con il termine elettronica ‒ per descrivere tutte le potenziali applicazioni alla trasmissione dell'informazione da parte di questa nuova sorgente di radiazione coerente, in alternativa ai dispositivi (per es. i transistor) che fanno uso di correnti elettriche e, quindi, di elettroni. In seguito al proliferare di nuove tipologie di sorgenti laser e, soprattutto, alla grande varietà di applicazioni che scaturivano da questa speciale e intensa sorgente di fotoni coerenti, il termine fotonica ha rapidamente ampliato il suo significato per abbracciare sia la disciplina scientifica che studia la generazione stessa di radiazione coerente sia il ventaglio di applicazioni, sempre più ampio e diversificato, che utilizzano sorgenti laser.

L'introduzione delle sorgenti di radiazione laser cambia la tradizionale descrizione dell'interazione tra radiazione e materia, basata su un approccio cosiddetto lineare, in cui cioè l'interazione stessa è indipendente dall'intensità di radiazione incidente. In altri termini, nell'approssimazione lineare, ai fini della specifica interazione luce-materia che si prende in esame, non è rilevante la quantità di luce incidente. Poiché le fonti naturali di radiazione luminosa e, più in generale, le sorgenti di luce incoerente (per es. le lampade a incandescenza) emettono luce con intensità generalmente trascurabile rispetto alle sorgenti coerenti (come il laser), gli usuali fenomeni di riflessione, rifrazione, rotazione della polarizzazione, dispersione della luce, da secoli illustrati nei testi di ottica, sono perfettamente descrivibili in regime lineare. L'introduzione del laser, invece, apre una finestra su una gamma totalmente nuova di interazioni luce-materia, denominate non-lineari, in quanto dipendenti dall'intensità della radiazione incidente.

Nel seguito si descriveranno i fondamenti dell'ottica non lineare, che sono anche alla base del funzionamento del laser stesso; verranno illustrate alcune delle recenti applicazioni dell'ottica non lineare, con particolare riguardo alla generazione di radiazione coerente; si daranno cenni su alcune delle nuove sorgenti laser, che consentono ormai di coprire gran parte delle regioni dello spettro elettromagnetico; si descriverà, infine, un nuovo sistema, il sintetizzatore di pettini ottici di frequenza (Optical frequency comb synthesizer, OFS), che contiene le innovazioni fotoniche più recenti e rappresenta un decisivo punto di svolta in molti settori di applicazione della fotonica.

Gli elementi fotonici essenziali in un OFS basato su laser Ti:Sa sono: la cavità laser, che utilizza una tecnica di aggancio in fase dei modi passiva, chiamata Kerr-lens mode-locking, e genera impulsi della durata tipicamente di qualche decina di fs; la fibra microstrutturata, che amplia lo spettro coperto dal pettine, consentendo la copertura di un'ottava; il cristallo non lineare, che, duplicando le frequenze più basse del pettine, consente di misurare la frequenza di offset. n

Elementi di ottica non lineare

Nei sistemi atomici e molecolari l'energia di legame dell'elettrone più esterno (quello più debolmente legato) è di circa 10 eV e la sua distanza dal nucleo è dell'ordine di 10⁻¹⁰ m. Pertanto, il campo equivalente che lega gli elettroni più esterni è dell'ordine di 1 GV/cm. Considerando che la maggior parte dei materiali dielettrici isolanti ha una soglia di rottura (breakdown) in corrispondenza di campi esterni applicati di circa 1 MV/cm, il massimo valore che può raggiungere il campo esterno è molto inferiore (di circa mille volte) al campo interno. È quindi giustificato espandere il momento di dipolo elettrico per unità di volume, denominato P, in serie di potenze del campo elettrico esterno applicato E:

[1] P(E) = ε₀χ(E)E = ε₀[χ⁽¹⁾E + χ⁽²⁾E² + χ⁽³⁾E³ +…].

dove ε₀ è la costante dielettrica assoluta del vuoto, χ è la suscettività elettrica e χ⁽ⁱ⁾ è la suscettività elettrica di ordine i-esimo. P è dunque una funzione di E che descrive la risposta del mezzo attraversato dall'onda elettromagnetica caratterizzata dal campo E. Con questa descrizione è immediato notare che, per valori di campo piccoli, tutti i termini di grado maggiore al primo diventano trascurabili e l'interazione è descrivibile arrestandosi al primo termine dell'espansione (termine lineare); è sufficiente, in altre parole, la sola conoscenza del termine di suscettività del primo ordine, χ⁽¹⁾.

In generale, la relazione tra P ed E richiede una conoscenza microscopica del mezzo attraversato dall'onda elettromagnetica o, in definitiva, della suscettività di ordine i-esimo χ⁽ⁱ⁾ per avere piena conoscenza degli effetti ottici di i-esimo ordine. D'altra parte, χ⁽ⁱ⁾ è una grandezza tensoriale (χ⁽¹⁾ è un tensore χ_ij di rango 2, χ⁽²⁾ è un tensore χ_ijk di rango 3, e così via) e può essere molto difficile da ricavare. Nel seguito, si descriveranno brevemente solo i fenomeni non lineari al secondo ordine (che dipendono cioè da χ⁽²⁾), tralasciando la descrizione dei fenomeni non-lineari di ordine superiore. Tenendo presente che χ⁽²⁾≠0 solo in mezzi privi di centro di simmetria, i processi al secondo ordine di maggiore rilevanza sono: somma e differenza di frequenza, ν₁−ν₂→ν₃ e ν₁+ν₂→ν₃ (si parla di 'duplicazione di frequenza' nel caso particolare di somma con la condizione ν₁=ν₂); generazione parametrica: ν₃→ν₁+ν₂.

La prima osservazione sperimentale della duplicazione di frequenza risale al 1961, a opera di Peter A. Franken e collaboratori i quali, utilizzando un cristallo di quarzo, generarono la seconda armonica, di lunghezza d'onda λ=3471 Å, di un laser a rubino con una lunghezza d'onda di emissione nel rosso (λ=6942 Å). Affinché i processi di conversione di frequenza sopra descritti possano avvenire, deve essere soddisfatto il principio di conservazione dell'energia. Per esempio, nel caso di generazione di frequenza somma, deve essere: hν₁+hν₂=hν₃. In effetti, una conversione efficiente dell'energia a nuove frequenze richiede anche la conservazione della quantità di moto che, nell'esempio citato, si traduce nell'equazione:

[2] ℏk₃− k₁− k₂ = 0

condizione detta di phase-matching, dove ℏk è la quantità di moto del fotone con lunghezza d'onda λ (λ=2π/|k|) e ℏ=h/2π, e la direzione del vettore k è quella di propagazione dell'onda. Il significato fisico della [2] è semplice, se consideriamo la natura ondulatoria dei fotoni: un'efficiente conversione dai campi a frequenza ν₁ e ν₂ a quello a frequenza ν₃ richiede interferenza costruttiva fra le tre onde in tutta la lunghezza del mezzo in cui avviene la conversione. Altrimenti, l'interferenza distruttiva riconverte energia dal campo a frequenza ν₃ verso i campi con frequenze ν₁ e ν₂ di partenza.

Tale approccio, in termini della polarizzazione del mezzo, è molto utile per descrivere le interazioni non lineari in mezzi trasparenti, come i cristalli usati per conversione di frequenza. Se però il mezzo attraversato dalla radiazione è risonante, cioè assorbe la radiazione che lo attraversa, si può utilizzare la cosiddetta matrice densità, che tiene conto anche degli effetti di coerenza, cioè della fase delle onde in relazione alla fase del mezzo che risponde all'onda che lo attraversa. Un simile approccio è però utilizzabile solo per un numero limitato di livelli energetici; se è possibile trascurare gli effetti di coerenza si può applicare il formalismo delle rate equations, che permette di descrivere lo scambio di fotoni tra il mezzo materiale e il campo elettromagnetico tramite un semplice sistema di equazioni differenziali. L'esempio più importante di interazione non lineare in mezzi assorbenti è sicuramente l'amplificazione di radiazione per emissione stimolata, che è alla base del funzionamento delle sorgenti laser.

Evoluzione delle sorgenti di radiazione coerente

Dall'introduzione del laser, nel 1960, è iniziata la ricerca di mezzi attivi che consentissero di coprire porzioni sempre più ampie dello spettro elettromagnetico. Contestualmente, per molte applicazioni del laser, si è manifestata l'esigenza di variare la frequenza di emissione in modo continuo (accordabilità in frequenza). Risultati soddisfacenti a entrambe le richieste si ottennero dapprima nel visibile, soprattutto grazie all'uso combinato di laser a ioni di argon e laser a coloranti. L'introduzione dei laser a semiconduttore consentì successivamente la copertura della regione dell'infrarosso vicino, anche grazie all'enorme impulso impresso dalla necessità di sviluppare sorgenti compatte ed economiche per i sistemi di telecomunicazione nelle regioni di massima trasparenza delle fibre ottiche, comprese tra 1,3 e 1,6 μm circa di lunghezza d'onda. Molto rilevante si rivelò anche lo sviluppo di sorgenti a stato solido, che utilizzano cioè cristalli di vari materiali come mezzo attivo. Esempi importanti in questa categoria sono: i laser operanti con cristalli costituiti da ioni neodimio in una matrice di YAG (Yttrium-Aluminum-Garnet, Y₃Al₅O₁₂), abbreviato Nd:YAG, e con l'emissione più intensa a 1,06 μm; i laser Ti:Sa (ioni titanio in matrice di zaffiro), in grado di coprire tutto l'intervallo spettrale compreso tra circa 700 e 1100 nm di lunghezza d'onda. I laser ad anidride carbonica, con mezzo attivo costituito da una miscela di gas, composta principalmente da He, N₂ e CO₂, sono rimasti per molti anni la principale sorgente nella regione tra 9 e 10 μm circa, con uno spettro discreto di righe. Più recentemente, sono state introdotte le sorgenti laser in fibra, con emissione tra 1 e 2 μm, che utilizzano un vetro drogato con ioni opportuni (per es., erbio o itterbio) come mezzo attivo e la fibra stessa come risonatore. Le regioni dello spettro che si sono rivelate più difficili da coprire con sorgenti laser accordabili in frequenza sono l'infrarosso (a lunghezze d'onda maggiori di circa 2 μm) e l'ultravioletto (fino ad alcuni nm in lunghezza d'onda).

Per l'infrarosso, soluzioni sono arrivate con l'introduzione di cristalli ferroelettrici (per es. LiNbO₃, LiTaO₃, KTP) con polarizzazione periodica, i quali, utilizzando il processo di quasi-phase-matching, garantivano efficienze di conversione della frequenza della radiazione almeno 10-20 volte superiore ai cristalli tradizionali, che fanno uso principalmente del phase-matching basato sulla birifrangenza. Nuovi sistemi basati sul processo di oscillazione parametrica e di generazione di frequenza, in questo nuovo genere di cristalli, hanno consentito, a partire dalla metà degli anni Novanta, un'ampia copertura spettrale dell'infrarosso, fino al limite di trasparenza dei cristalli utilizzati per la generazione (intorno a 4,5 μm). Parallelamente, si sviluppavano nei Bell Laboratories (Stati Uniti), a opera del gruppo di Federico Capasso, nuove sorgenti laser ('a cascata quantica'), basate sulla tecnologia dei semiconduttori, ma con emissione nell'infrarosso, fino a lunghezze d'onda di circa 100 μm.

La frequenza di emissione dei laser a semiconduttore convenzionali è determinata dall'energia dei fotoni emessi nel passaggio degli elettroni dalla banda di conduzione alla banda di valenza, ed è quindi vincolata alla differenza (gap) di energia esistente tra le due bande. Inoltre, ogni elettrone che passa in banda di valenza genera un solo fotone. È però molto difficile trovare semiconduttori con gap sufficientemente piccole da consentire emissione laser a lunghezze d'onda di alcuni micron. I laser a semiconduttore a cascata quantica (QCL), d'altra parte, sono basati sulla deposizione successiva di strati sottilissimi (dello spessore di alcuni nanometri) di semiconduttori, che consentono di controllare i livelli di energia, le funzioni d'onda elettroniche e la struttura delle bande, in maniera da ottenere le prestazioni desiderate. In questo modo, gli elettroni compiono salti di energia definiti a priori, ma sempre all'interno della banda di conduzione, e quindi la differenza di energia, cioè la frequenza dei fotoni, non è più limitata dalla gap tra la banda di valenza e quella di conduzione. Inoltre, è importante notare che la potenza emessa P=ηhν(I−I_th)/2e (dove hν è l'energia del singolo fotone emesso, I e I_th sono rispettivamente la corrente fornita e quella di soglia (threshold), cioè la minima necessaria per avere emissione laser, η è un coefficiente che dipende dalle proprietà della cavità ottica del laser ed e è la carica dell'elettrone) diminuisce proporzionalmente alla frequenza ν della radiazione emessa e cresce in proporzione alla corrente fornita. I laser QCL, quindi, hanno un duplice vantaggio rispetto a quelli convenzionali, in termini di potenza emessa: possono sostenere correnti anche dieci volte superiori e ogni elettrone, grazie a un meccanismo a cascata, genera tipicamente alcune decine di fotoni. Con tale tecnologia sono stati costruiti laser con emissione continua, a temperatura vicina a quella ambiente e con potenze di emissione anche di alcuni watt.

Per quanto riguarda la copertura della regione a lunghezze d'onda inferiori a 400 nm, un possibile approccio è la generazione per duplicazione di frequenza, anche ripetuta, in cristalli non lineari, in modo simile a quanto descritto per la generazione in differenza di frequenza nell'infrarosso. Il limite a frequenze alte è ancora la regione di trasparenza dei cristalli disponibili: con il BBO (β-BaB₂O₄) si può arrivare fino a circa 250 nm. L'altra tecnica è basata sulla generazione di armoniche di ordine elevato mediante la focalizzazione in gas di impulsi ultracorti (della durata di circa 10⁻¹⁴ s per ogni singolo impulso), con intensità dell'ordine di 10¹⁶ W/cm². A questi valori di intensità, il campo elettrico della radiazione laser è superiore a quello che lega gli elettroni più interni negli atomi dei gas nobili. In queste condizioni, non è possibile espandere la polarizzazione P indotta dal laser nel gas in serie di potenze, come riportato nella [1], in quanto il campo esterno non può essere considerato una perturbazione rispetto a quello atomico di legame, e la serie non risulta convergente. L'effetto fisico che si ottiene è la generazione di radiazione a frequenze multiple (armoniche) dispari della frequenza del laser di partenza. Poiché con simile efficienza possono essere generati ordini anche molto elevati di armoniche (oltre la centesima), tale processo consente di coprire la regione compresa tra 1 e 100 nm. Il meccanismo fisico essenziale alla base di questo tipo di generazione è la ionizzazione degli atomi neutri da parte dell'intenso campo laser; l'elettrone è quindi accelerato dal campo stesso e, in determinate condizioni, ritorna sullo ione, si ricombina e riemette sotto forma di fotoni armonici l'energia ricevuta dal laser.

Un nuovo sistema per la fotonica: l'OFS

Per molti anni, la tecnologia per la generazione di impulsi ultracorti (impulsi di durata di decine di femtosecondi (fs), con 1 fs=10⁻¹⁵ s) si è evoluta trovando principale applicazione nella chimica e nella biologia, che sfruttano in particolare la brevissima durata degli impulsi per 'congelare' la dinamica dei legami molecolari, in analogia con i tempi di apertura e chiusura degli otturatori delle macchine fotografiche. Parallelamente, si sviluppavano standard di frequenza basati su sorgenti ad alta stabilità e altamente monocromatiche, con emissione di radiazione rigorosamente non impulsata ma continua (CW). L'utilizzo di elaborate e dispendiose 'catene di frequenza', costituite da molti oscillatori laser con emissione continua, consentiva di trasferire l'unico standard assoluto di frequenza ‒ la transizione tra livelli iperfini del ¹³³Cs, impiegata per definire l'unità di tempo, il secondo ‒ dalle microonde all'infrarosso e al visibile. Dal 1999, principalmente a opera di Theodor W. Hänsch e John L. Hall, si intuisce che le sorgenti di impulsi ultracorti di radiazione possono servire come ponte naturale per trasferire lo standard assoluto di frequenza ad altre regioni dello spettro.

Per comprendere il legame che esiste tra un treno di impulsi laser nel dominio del tempo e la sua rappresentazione nel dominio della frequenza, è possibile decomporre ogni singolo impulso in una funzione inviluppo, V_e(t), sovrapposta a un'onda portante a frequenza ω_p. Il campo elettrico dell'impulso è allora esprimibile come V(t)=V_e(t)exp(iω_pt). La differenza di fase, ϕ_pe, tra la funzione inviluppo e l'onda portante, si può allora definire come lo spostamento di fase tra il picco di V_e(t) e il picco più vicino dell'onda portante. Tipicamente, la fase ϕ_pe varia nei mezzi dispersivi, nei quali le diverse lunghezze d'onda viaggiano a differenti velocità, dando luogo a una differenza tra velocità di gruppo e velocità di fase. Quando ϕ_pe si mantiene costante nel tempo, tutti gli impulsi emessi dal laser sono identici, con uguale fase. Se si considera la trasformata di Fourier di un singolo impulso, passando dal dominio del tempo a quello della frequenza, si troverà che a durate temporali più brevi corrisponderà un contenuto di frequenze più ampio, limitando la massima risoluzione in frequenza ottenibile all'inverso della durata temporale dell'impulso. Ciò spiega l'incompatibilità, sopra menzionata, che per molti anni ha caratterizzato lo sviluppo di laser a impulsi ultracorti rispetto alle applicazioni che richiedevano sorgenti di radiazione a elevata purezza spettrale, sostanzialmente monocromatiche, come la spettroscopia ad alta risoluzione e gli standard di frequenza.

fig. 2

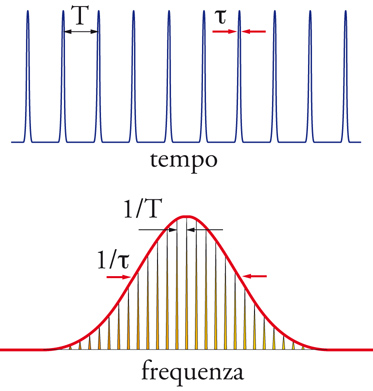
Se, però, al singolo impulso si sostituisce idealmente un numero infinito di impulsi che hanno tutti la stessa fase e sono tutti egualmente spaziati, lo spettro di Fourier risultante nel dominio delle frequenze consisterà di un 'pettine' di righe egualmente spaziate da una frequenza pari all'inverso del tempo intercorrente tra un impulso e il successivo, che è pari alla cosiddetta frequenza di ripetizione f_rep del laser che emette gli impulsi. La spiegazione fisica di questa operazione matematica è la seguente: qualsiasi spettrometro che possieda una risoluzione in frequenza tale da distinguere i singoli 'denti' del pettine di frequenze, non può avere una risoluzione temporale sufficiente a separare impulsi successivi. Di conseguenza, gli impulsi successivi che incidono sullo spettrometro interferiranno tra loro e l'interferenza costruttiva cui periodicamente danno luogo creerà il 'pettine' di denti egualmente spaziati, nel dominio della frequenza. Se invece la fase ϕ_pe non è costante nel tempo, ma c'è una variazione di fase costante Δϕ_pe tra ogni impulso e il successivo, il pettine di denti, nel dominio della frequenza, traslerà rigidamente e le frequenze ottiche, ν_n, del pettine di righe, si potranno esprimere come ν_n=nf_rep+f₀, dove f₀ è la frequenza di offset del pettine, definita come f₀=f_repΔϕ_pe(1/2π). Le relazioni tra gli impulsi emessi, nel dominio del tempo, e il corrispondente spettro nel dominio della frequenza, sono riassunte in fig. 2. Dalla descrizione fin qui data, emerge chiaramente il 'ponte' che l'OFS crea tra le frequenze a microonde e le frequenze visibili. Infatti, ogni frequenza nel visibile è esprimibile mediante la frequenza di ripetizione del laser, f_rep (tipicamente nell'intervallo 0,1÷2 GHz), e una frequenza fissata, f₀. È quindi possibile riferire la frequenza f_rep allo standard assoluto, per esempio attraverso un sistema GPS (Global positioning system) e misurare f₀ per avere disponibile nel visibile un 'righello' naturale rispetto al quale misurare qualsiasi frequenza compresa nell'intervallo coperto dall'OFS. Il metodo più semplice e utilizzato per la misura di f₀ è la generazione di un pettine che copre un'ottava, cioè che contiene tutti i denti dalla frequenza ν a frequenza 2ν. In tal modo, duplicando in un apposito cristallo non lineare la parte del pettine a più bassa frequenza (per es., il dente ν_n viene duplicato in frequenza e diventa 2ν_n) e confrontando, per mezzo di un battimento eterodina, con la parte del pettine a frequenza più elevata (per es., con il dente ν_2n) si ottiene: 2ν_n−ν_2n=2(nf_rep+f₀)−(2nf_rep+f₀)=f₀, che è proprio la frequenza che si intendeva misurare.

È chiaro che tale approccio è perseguibile solo avendo un pettine di frequenze sufficientemente ampio. Per le regole della trasformata di Fourier prima citate, la durata degli impulsi, per esempio di un laser Ti:Sa a circa 800 nm, dovrebbe essere solo di qualche fs, cioè di un solo ciclo ottico. Data la difficoltà di tale tecnologia, il metodo più diffuso per ampliare lo spettro in frequenza del pettine utilizza le cosiddette fibre microstrutturate, chiamate anche photonic crystal fibers, per la loro speciale struttura che alterna, in modo regolare e predefinito, vuoti e vetro, permettendo di ottenere un elevato contrasto di indice di rifrazione. In tal modo, si ottiene un core effettivo molto piccolo e una dispersione controllata, con un confinamento spaziotemporale degli impulsi molto elevato. Ciò permette di avere effetti non lineari particolarmente rilevanti nel percorso compiuto dalla radiazione all'interno di queste fibre ottiche, consentendo un ampliamento significativo del contenuto spettrale (vale a dire i denti) del pettine.

Bibliografia

Bellini 2002: Bellini, Marco, Armoniche laser e supercontinuo: proprietà di coerenza di sorgenti di radiazione estreme, "Il Nuovo Saggiatore", 18, 2002, pp. 43-51.

Boyd 2003: Nonlinear optics, 2. ed., edited by Robert W. Boyd, Amsterdam-London, Academic Press, 2003.

Capasso 2002: Capasso, Federico e altri, Quantum cascade lasers, "Physics today", 55, 2002, pp. 35-40.

Hannaford 2005: Femtosecond laser spectroscopy, edited byPeter Hannaford, New York, Springer, 2005.

Menzel 2000: Menzel, Ray, Photonics: linear and nonlinear interactions of laser light and matter, Berlin, Springer, 2000.