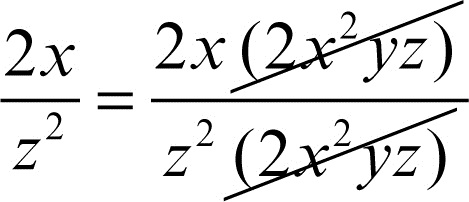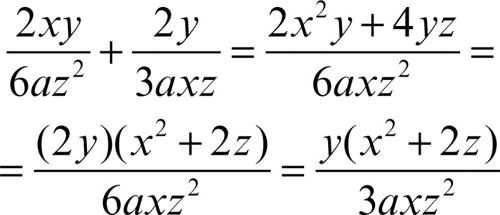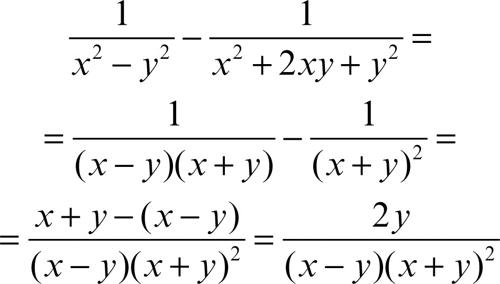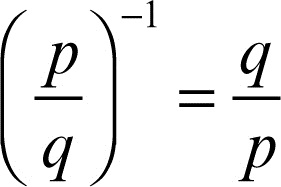frazione algebrica

frazione algebrica

frazione algebrica espressione del tipo p/q, dove p e q sono polinomi, in una o più incognite, contenenti o meno parametri. In altre parole, una frazione algebrica è un’espressione frazionaria in cui si ammette che siano presenti delle lettere incognite al denominatore, come per esempio nel caso

I polinomi costituiscono un caso particolare di frazioni algebriche, in cui il polinomio al denominatore è costante. L’insieme delle frazioni algebriche è un ampliamento dell’insieme dei polinomi, in cui si ammette che due polinomi possano anche essere divisi l’uno per l’altro (a patto che il divisore sia diverso dal polinomio nullo). È possibile operare con le frazioni algebriche seguendo le stesse regole formali usate nelle operazioni tra frazioni: le frazioni algebriche possono dunque essere sommate, sottratte, moltiplicate e divise le une con le altre e se ne possono calcolare le potenze o le radici.

Come nel caso dei polinomi, in una frazione algebrica è possibile attribuire dei valori numerici alle incognite e ai parametri, così da ottenere un valore numerico. Se per esempio p(x) e q(x) sono due polinomi, allora p(x)/q(x) è una frazione algebrica, che è definita per tutti i valori reali per cui q(x) ≠ 0. Tale frazione algebrica definisce a sua volta la funzione razionale y = p(x)/q(x); l’insieme dei valori reali per cui il denominatore della frazione algebrica è diverso da zero è talvolta detto insieme di definizione o anche campo di esistenza della frazione algebrica (non si tratta però di un campo in senso algebrico): esso coincide con l’insieme in cui è definita la funzione associata. Per esempio, nel caso della frazione algebrica a valori reali

il suo insieme di definizione è l’insieme delle coppie di numeri reali (x, y) per cui x ≠ ±1. Due frazioni algebriche p/q e p′/q′ si dicono equivalenti se pq′ = qp′; due frazioni algebriche sono equivalenti se sono ottenibili l’una dall’altra moltiplicando o dividendo numeratore e denominatore per uno stesso polinomio non nullo. Modulo tale equivalenza, l’insieme delle frazioni algebriche viene dunque a coincidere con l’insieme delle funzioni razionali.

Una frazione algebrica si dice ridotta ai minimi termini se il numeratore e il denominatore sono polinomi primi fra loro, vale a dire se non esistono polinomi non costanti che li dividano entrambi. Per ridurre una frazione algebrica ai minimi termini bisogna dividere numeratore e denominatore per il loro massimo comune divisore (mcd): questa operazione viene detta semplificazione della frazione algebrica; più in generale si parla di semplificazione di una frazione algebrica ogni qual volta si dividono numeratore e denominatore per uno stesso fattore comune. Per esempio, la frazione algebrica

non è ridotta ai minimi termini in quanto numeratore e denominatore sono ambedue divisibili per il polinomio 2x ²yz: la frazione algebrica semplificata sarà dunque la frazione algebrica equivalente

ottenuta dividendo numeratore e denominatore per il fattore comune 2x ²yz. Per semplificare una frazione algebrica è talvolta necessario scomporre in fattori i polinomi che ne costituiscono il numeratore o il denominatore: a tal fine, risultano utili i raccoglimenti a fattor comune e il riconoscimento dei prodotti notevoli (→ polinomio, scomposizione in fattori di un).

Per addizionare o sottrarre due frazioni algebriche con lo stesso denominatore, basta addizionare o sottrarre i numeratori lasciando invariato il denominatore. Per addizionare o sottrarre due frazioni algebriche con diversi denominatori, ci si riconduce al caso in cui il denominatore sia lo stesso attraverso la riduzione a denominatore comune, vale a dire si determinano due forme equivalenti alle due frazioni algebriche date in modo che abbiano lo stesso denominatore. La somma e la sottrazione potranno in questo modo essere effettuate sulle due forme equivalenti. Come denominatore comune è opportuno scegliere il minimo comune multiplo (mcm) dei denominatori delle due frazioni algebriche. Per esempio, volendo addizionare

si considera il minimo comune multiplo dei denominatori, 6axz², e le due frazioni algebriche, espresse in questo denominatore, sono rispettivamente

Si ottiene dunque

Analogamente si opera se le due frazioni algebriche presentano al denominatore polinomi che non sono monomi, dopo averli opportunamente scomposti in fattori. Per esempio:

Il prodotto di due frazioni algebriche si ottiene moltiplicando fra loro rispettivamente i numeratori e i denominatori delle due frazioni algebriche

Ogni frazione algebrica diversa da zero (il cui numeratore sia cioè diverso da zero) è invertibile, vale a dire esiste una frazione algebrica, detta la sua inversa (indicata con l’esponente ⁻¹), che moltiplicata per essa dà risultato 1: essa si ottiene scambiando il numeratore p e il denominatore q della frazione algebrica da invertire:

Per dividere due frazioni algebriche si moltiplica la prima per l’inversa della seconda: