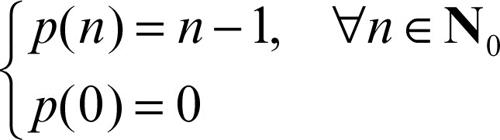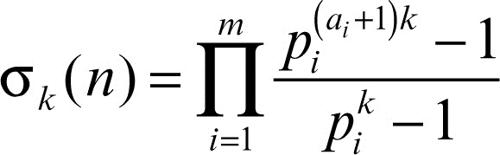funzione aritmetica

funzione aritmetica

funzione aritmetica funzione definita sull’insieme N dei numeri naturali. Semplici funzioni aritmetiche sono, per esempio, la funzione successore, definita come s(n) = n + 1 per ogni n ∈ N, e la funzione predecessore p(n) che è definita per casi nel modo seguente:

avendo indicato con N₀ l’insieme dei numeri naturali diversi da 0. Altri esempi di funzioni aritmetiche sono: la funzione d(n), che dà il numero di divisori di n, compresi 1 e n; la funzione σ(n), che dà la somma dei divisori stessi, e in generale le funzioni σ_k(n), che danno la somma delle potenze k-esime dei divisori di n, per cui d(n) = σ(n), σ(n) = σ₁(n). Per esempio, poiché i divisori di 12 sono 1, 2, 3, 4, 6 e 12, risulta d(12) = 6, σ(12) = 28, σ₂(12) = 210. La formula generale per σ_k(n), se

è:

con d(n) = m. Tutti i precedenti sono esempi di funzioni in cui anche il codominio è N e nella cosiddetta teoria della calcolabilità è questo il significato ristretto che si dà alla locuzione funzione aritmetica, dal momento che un effettivo sistema di calcolo opera necessariamente su un sottoinsieme di N. In altri ambiti, in particolare in teoria dei numeri, non si pongono restrizioni al codominio e dunque è detta funzione aritmetica una funzione da N a C: in tale contesto essa è quindi una successione di numeri complessi.

Una funzione aritmetica è detta moltiplicativa se ƒ(ab) = ƒ(a)ƒ(b) per ogni coppia di numeri a e b primi tra loro; è tale per esempio la funzione toziente di → Eulero. Una funzione aritmetica è completamente moltiplicativa se la relazione ƒ(ab) = ƒ(a)ƒ(b) è vera per ogni coppia di numeri naturali non nulli. Una funzione aritmetica è detta additiva se ƒ(ab) = ƒ(a) + ƒ(b) per ogni coppia di numeri naturali primi tra loro; completamente additiva se la relazione vale per ogni coppia di numeri interi positivi. È tale per esempio la funzione logaritmo ristretta ai numeri interi positivi.