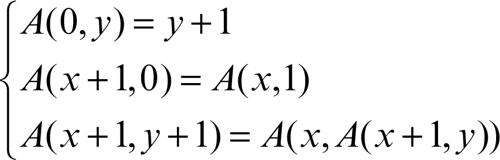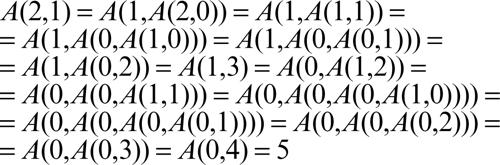Ackermann, funzione di

Ackermann, funzione di

Ackermann, funzione di esempio di → funzione ricorsiva che non è ricorsiva primitiva (→ funzione ricorsiva primitiva). Hilbert formulò l’ipotesi che ogni funzione calcolabile fosse ricorsiva primitiva, cioè ottenibile dalle funzioni di base (funzione zero, funzione successore e funzioni di proiezione) tramite i procedimenti di composizione e ricorsione. Tale affermazione si rivelò infondata quando nel 1928 Ackermann definì una nuova funzione calcolabile, ma non ricorsiva primitiva, poiché per ottenerla è necessario un ulteriore procedimento, detto di minimalizzazione. Questa funzione, che porta il suo nome e che qui di seguito è indicata con A, ha come dominio l’insieme dei numeri naturali N ed è definita nel modo seguente:

Per comprendere il suo modo di operare, si può verificare, per passi successivi, che A(2,1) = 5:

La funzione è calcolabile; tuttavia si può dimostrare che non è ottenibile soltanto per composizione e ricorsione di funzioni di base. Per definirla si deve ricorrere a un procedimento basato sull’applicazione di un operatore di → minimalizzazione, che data una funzione ricorsiva in n + 1 variabili permette di costruirne un’altra in n variabili.