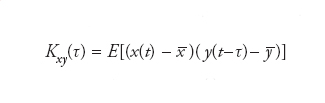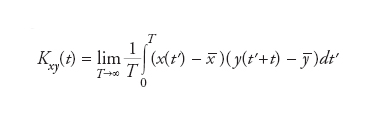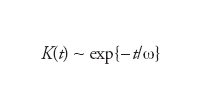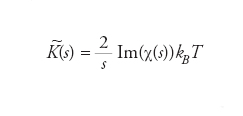funzione di correlazione
funzione di correlazione
Definita matematicamente come il momento misto
di due processi stocastici x(t) e y(t) con sfasamento temporale τ, dove −x=E[x(t)] e −y=E[y(t)] sono i valori attesi (valori medi) dei due processi. Se questi ultimi sono stazionari, ovvero le loro proprietà sono indipendenti per traslazioni temporali, la funzione di correlazione dipende unicamente dallo sfasamento τ. L’importanza pratica della funzione di correlazione è nel suo ruolo di misura dell’indipendenza statistica: essa è infatti pari a zero se i due processi sono completamente scorrelati. In fisica statistica, la funzione di correlazione è utilizzata per caratterizzare la relazione tra grandezze fluttuanti x(t) e y(t) ed è calcolata (ponendo l’origine dei tempi a t=0) a partire dalla formula
Se nella formula precedente alla variabile y(t) si sostituisce la stessa x(t) si ottiene una grandezza detta autocorrelazione. Nel caso di processi non stazionari, si considera spesso il comportamento asintotico (per t→∞) della correlazione, che in molti casi presenta una decrescita esponenziale del tipo
Il parametro ω è dunque una misura della correlazione ed è detto tempo di correlazione: per t>ω quest’ultima diviene trascurabile. In meccanica statistica, la funzione di correlazione è particolarmente significativa poiché produce una relazione con la temperatura del sistema che costituisce il contenuto della teoria della fluttuazione-dissipazione. Indicando con T la temperatura assoluta e con ∼K(s) la trasformata di Fourier di K(t), essa è espressa dalla formula
La funzione χ(s) è chiamata suscettibilità del materiale, Im(χ(s)) è la sua parte immaginaria e k]] la costante di Boltzmann. È importante ricordare che fluttuazioni casuali sono presenti anche in contesti diversi. Per es., nei sistemi disordinati la posizione degli atomi o molecole componenti è una variabile casuale e dalla sua funzione di autocorrelazione (nota anche con il nome di distribuzione radiale) è possibile ricavare in alcuni casi l’equazione di stato.
→ Frattali