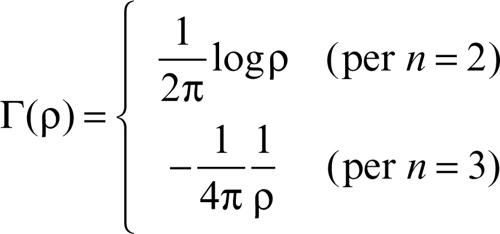Green, funzione di
Green, funzione di
Green, funzione di (di prima specie) in analisi, per l’equazione di → Poisson Δu = ƒ, è una funzione che permette di scrivere la soluzione del problema di → Dirichlet u = φ su ∂Ω. Introdotta la soluzione fondamentale (dato di Dirichlet)
che è la soluzione (a simmetria radiale) dell’equazione Δu = δ, dove δ è la distribuzione delta di → Dirac, e fissato un punto P ∈ Ω, si determini una funzione armonica h(Q) tale che h(Q) = − Γ(|P − Q|) su ∂Ω. Allora la funzione di Green
permette di scrivere la soluzione del problema di Dirichlet nella forma
Basterebbe, quindi, saper risolvere un problema di Dirichlet (col dato Γ dipendente da P) per risolverli tutti. Nella pratica non è però semplice trovare la funzione h, e quindi neppure la G; i due casi più semplici conducono alle cosiddette formule di Poisson:
