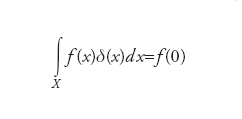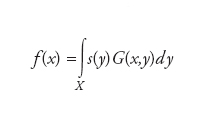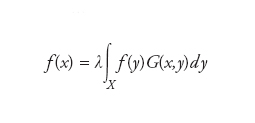funzione di Green

funzione di Green

Una funzione legata alla rappresentazione tramite integrali di soluzioni di equazioni differenziali (su una regione X⊂ℝ^{[) con condizioni al bordo (della regione X, indicato usualmente con il simbolo fX). La funzione di Green G di un problema al bordo per un’equazione differenziale lineare è quella soluzione fondamentale dell’equazione stessa che soddisfa condizioni al bordo omogenee (ovvero della forma B_∥G=0, dove gli operatori B_∥ sono appunto definiti sul bordo). Più precisamente, se D è un operatore differenziale lineare (sufficientemente regolare) definito sulla regione X⊂ℝ^{[ con bordo fX, allora una funzione generalizzata (distribuzione) è la funzione di Green di D se DG(x,y)=δ(x−y), dove x,y∈X e δ(x) è la funzione delta di Dirac definita dalla formula

per ogni f continua su X. Una soluzione particolare dell’equazione Df(x)=s(x) (con s(x) opportuna) è fornita dalla formula

La soluzione generale è quindi come sempre ottenuta aggiungendo una soluzione dell’equazione omogenea Df(x)=0. Alter­nativamente, la funzione di Green può essere definita come nucleo integrale dell’operatore inverso dell’operatore differenziale generato dalla data equazione differenziale con le specifiche condizioni al bordo. Infatti, formalmente dall’equazione Df(x)=s(x) ricaviamo f(x)=D⁻¹s(x), dove D⁻¹ indica l’inverso di D. Determinare la funzione di Green, dunque, riduce lo studio delle proprietà di un operatore differenziale allo studio di quelle del corrispondente operatore integrale. In particolare, il problema agli autovalori Df(x)=f(x) è equivalente all’equazione integrale

alla quale si può applicare la teoria di Fredholm. La teoria delle funzioni di Green è stata in particolare sviluppata per lo studio di equazioni differenziali alle derivate parziali ellittiche e iperboliche, per es., rispettivamente l’equazione del calore e delle onde o di Klein-Gordon. In quest’ultimo caso a partire dalle funzioni di Green si costruiscono i propagatori di Feynmann, di fondamentale importanza nella teoria quantistica dei campi.

→ Equazioni differenziali: problemi non lineari