funzione di n variabili

funzione di n variabili

funzione di n variabili funzione che dipende da n variabili indipendenti. Se le variabili sono poche, si

usa denominarle con lettere diverse, e indicare la funzione con una scrittura come ƒ(x, y), ƒ(x, y, z) ecc. Se le variabili sono numerose o non si vogliono precisare, si raccolgono in un vettore x = (x₁, x₂, ..., x_n) e si scrive ƒ(x). Le definizioni date per le funzioni in una variabile (→ funzione) si estendono con opportune modifiche alle funzioni a più variabili.

Per le funzioni in due varabili, una variabile z si dice funzione delle due variabili indipendenti x e y e si scrive z = ƒ(x, y) se, a ogni coppia ordinata di valori di x e y, appartenenti all’insieme su cui la funzione è definita, resta determinato uno e un solo valore di z.

Per esempio,

sono esempi di funzioni di due variabili. Per la rappresentazione del grafico di una funzione di due variabili si ricorre a una terna di assi cartesiani e la funzione risulta rappresentata da una superficie dello spazio ordinario che gode della proprietà di essere incontrata in un solo punto dalle parallele all’asse z (una superficie di questo tipo è detta superficie topografica). Il dominio in cui possono variare x e y generalmente non abbraccia l’intero piano bensì una sua parte finita o infinita limitata da uno o più contorni costituiti da uno o più archi di → Jordan che tutti assieme costituiscono la frontiera del dominio (spesso il termine dominio è riservato al caso in cui tale frontiera appartenga all’insieme di variabilità di x e y, mentre si parla di campo o regione quando parte della frontiera o tutta la frontiera stessa non è inclusa nell’insieme).

Lo stesso linguaggio si mantiene nel caso di funzioni di più di due variabili e si parla di funzioni definite in un dominio dello spazio n-dimensionale e di grafico di una funzione di n variabili come ipersuperficie (n − 1)-dimensionale rappresentata in un iperspazio cartesiano a n dimensioni. Per tale estensione si definisce intorno circolare di un punto P₀(x₁⁽⁰⁾, x₂⁽⁰⁾, x₃⁽⁰⁾, ..., x_n⁽⁰⁾), di raggio r, dello spazio n-dimensionale, l’insieme dei punti (x₁ x₂, x₃, ..., x_n) per cui

dove si pone ≤ oppure < a seconda che la frontiera sia o meno inclusa. Similmente si definisce un intorno rettangolare di un punto P₀(x₁⁽⁰⁾, x₂⁽⁰⁾, x₃⁽⁰⁾, ..., x_n⁽⁰⁾) dello spazio a n dimensioni (detto anche cella) l’insieme di punti (x₁, x₂, x₃, ...., x_n) per cui sono soddisfatte n disuguaglianze del tipo

Con queste definizioni si dice che la funzione ƒ tende al limite λ per P tendente a P₀ e si scrive

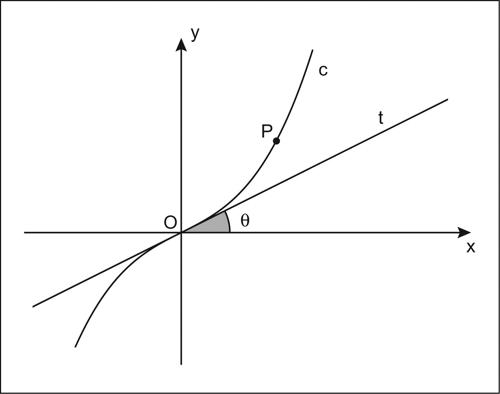
se, dato il numero positivo ɛ, si può determinare un intorno I del punto P₀ tale che in tutti i punti di questo intorno, tranne al più nel punto P₀, sia soddisfatta la diseguaglianza | ƒ(P) − λ | < ɛ. Se n > 3 si intende che l’intorno di cui parla questa definizione è un intorno circolare oppure una cella. La definizione di limite si modifica in modo ovvio quando λ = ∞ oppure quando il punto P₀ è all’infinito. Per il limite di una funzione di n variabili valgono le proprietà che si stabiliscono per i limiti di una funzione di una variabile (→ limite). Tuttavia il limite di una funzione di più variabili ha alcune caratteristiche che lo differenziano da quello di una funzione di una variabile. Si può mostrare che già nel caso di due variabili, può esistere il limite di ƒ(x, y) allorché il punto (x, y) si avvicina a (x₀, y₀) lungo una speciale direzione pur non esistendo il limite di ƒ(x, y) per x → x₀ e y → y₀. Per esempio, la funzione z = y /x non ha alcun limite per (x, y) → 0 (perché il rapporto y /x prende qualsiasi valore in qualsiasi intorno dell’origine). Se tuttavia si fa avvicinare il punto P(x, y) all’origine muovendo su una curva c passante per O e avente in O una determinata tangente t, si ha

essendo θ l’angolo che la tangente t forma con l’asse delle ascisse.

La definizione di continuità di una funzione di n variabili è del tutto analoga a quella di una funzione di una variabile: ƒ(P) è continua in P₀ se esiste il suo limite per P → P₀ ed è uguale a ƒ(P₀). La definizione di derivata di una funzione di n variabili porta all’introduzione di → derivate parziali rispetto a ciascuna delle variabili indipendenti della funzione.

Anche per le funzioni di più variabili si ricercano i valori di massimo e di minimo nonché i punti stazionari del loro grafico. Si dimostra che condizione necessaria affinché una funzione derivabile di n variabili ƒ(x₁, x₂, ..., x_n) sia massima o minima in un punto interno al suo campo di definizione è che in tale punto siano nulle le derivate parziali della funzione rispetto a tutte le sue variabili:

(→ massimo; → massimo vincolato; → minimo).