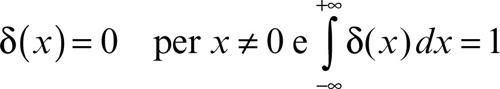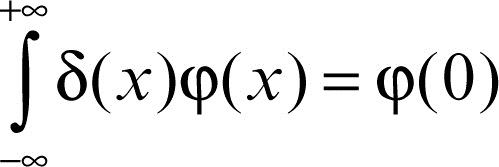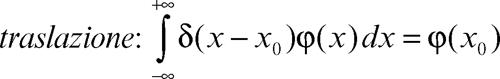funzione impulsiva
funzione impulsiva
funzione impulsiva altra denominazione della funzione di Dirac, detta anche delta di Dirac o impulso ideale; in analisi e nelle sua applicazioni alla fisica, è una distribuzione (o funzione generalizzata). È possibile pensare alla funzione impulsiva, indicata con il simbolo δ(x), come al limite di una sequenza di funzioni che sono diverse da 0 in un insieme sempre più piccolo e che hanno un picco sempre più alto, il cui integrale è sempre uguale a 1:
Un tale oggetto non è una vera funzione, ma può essere definito rigorosamente mediante la sua azione su una funzione regolare φ(x):
Da un punto di vista fisico la funzione impulsiva può rappresentare “oggetti” come un segnale impulsivo di durata istantanea, la densità di massa o la densità di carica di un punto materiale. La funzione impulsiva gode delle seguenti proprietà:
La funzione impulsiva è la derivata della → funzione gradino. Il suo prodotto di convoluzione con una funzione è dato da: g(x) ∗ δ(x − x0) = g(x − x0). La trasformata di Fourier della funzione impulsiva è la funzione costante uguale a 1.