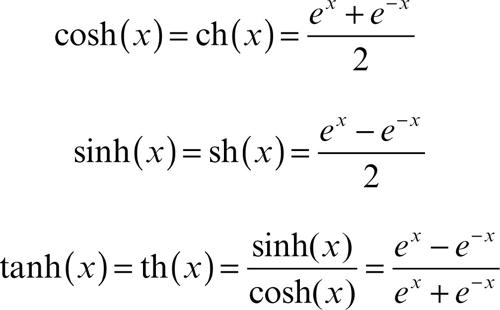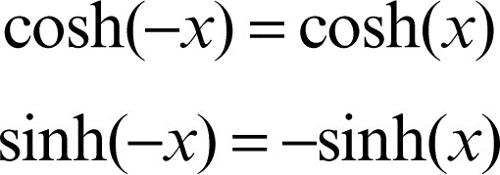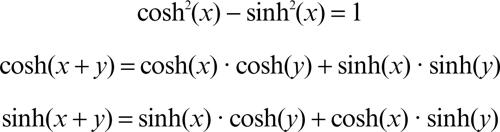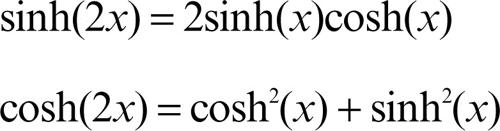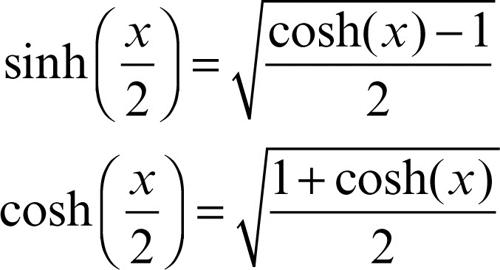funzione iperbolica
funzione iperbolica
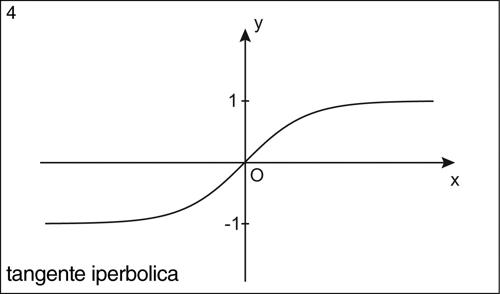
funzione iperbolica particolare funzione definita a partire dalla funzione esponenziale. Le principali funzioni iperboliche sono le funzioni seno iperbolico, coseno iperbolico e tangente iperbolica, definite dalle identità:
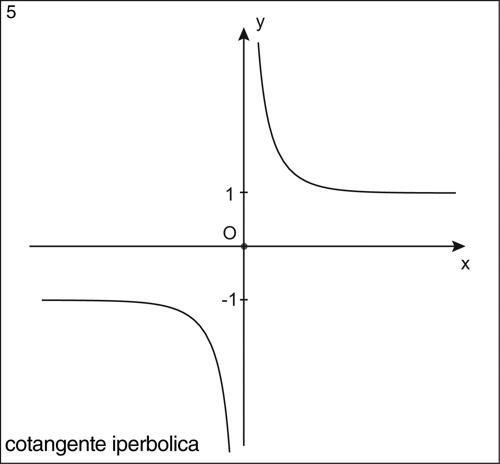
Similmente al caso goniometrico, si possono definire le altre funzioni iperboliche a partire dal coseno e dal seno iperbolici: la cotangente iperbolica, indicata con il simbolo coth e definita da
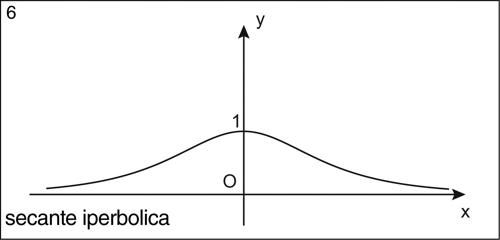
la secante iperbolica, indicata con il simbolo sech e definita da
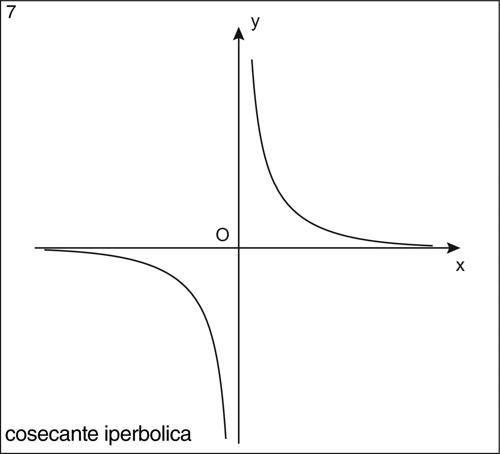
e infine la cosecante iperbolica, indicata con il simbolo csch e definita da
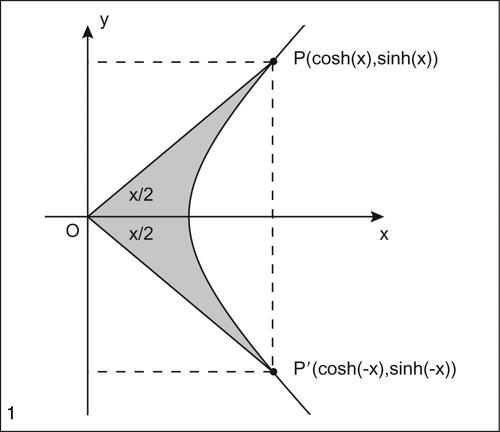
Tali funzioni hanno proprietà analoghe a quelle delle funzioni goniometriche e la loro denominazione deriva dal fatto che sono definite a partire dall’iperbole equilatera x 2 − y 2 = 1 anziché dalla circonferenza unitaria x 2 + y 2 = 1 (→ funzione goniometrica). Più in particolare, in un riferimento Oxy si considera il ramo destro dell’iperbole equilatera x 2 − y 2 = 1 e il suo punto d’intersezione con l’asse delle ascisse H = (1, 0). Dato un numero reale positivo x, si considera il punto P nel primo quadrante tale che il settore iperbolico di vertice O delimitato dai segmenti OH e OP abbia area x/2. Si definiscono allora il coseno iperbolico e il seno iperbolico di x, indicati rispettivamente con cosh(x) e sinh(x), rispettivamente come l’ascissa e l’ordinata di tale punto P.
Se invece x è negativo, si determina, in modo analogo, il punto P′ nel quarto quadrante in modo che il settore iperbolico con vertice in O e delimitato dai segmenti OH e OP′ abbia area |x|/2, e si definiscono il suo coseno iperbolico e il suo seno iperbolico rispettivamente come la sua ascissa e la sua ordinata. Detto altrimenti, P′ è il simmetrico di P rispetto all’asse delle ascisse e valgono dunque le uguaglianze:
Al variare di x, il coseno iperbolico e il seno iperbolico definiscono delle funzioni di variabile reale, che sono rispettivamente una funzione pari e una funzione dispari.
L’iperbole equilatera di equazione x 2 − y 2 = 1 ammette quindi la rappresentazione parametrica x = cosh(t), y = sinh(t). Il legame tra funzioni iperboliche e goniometriche si manifesta nel campo complesso, dove queste funzioni appaiono ottenute le une dalle altre mediante semplici rotazioni del piano complesso, espresse dalle formule cosh(iz) = cos(z), sinh(iz) = i ⋅ sin(z). A ogni formula goniometrica corrisponde così una analoga formula nella trigonometria iperbolica, tra cui notevoli sono le identità
Da queste si deducono le formule di duplicazione:
Valgono inoltre le formule di bisezione:
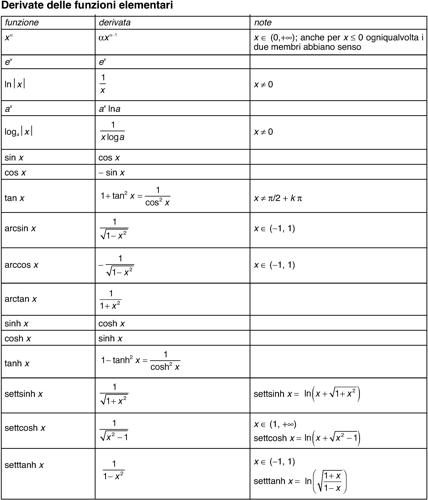
Ogni altra formula (per esempio, le formule di prostaferesi) si può ottenere dalla corrispondente formula per le funzioni goniometriche sostituendo cosh(x) a cos(x), sinh(x) a sin(x) e cambiando il segno dei termini in cui compare sinh2(x). Importante è pure l’identità ex = cosh(x) + sinh(x), che esprime la funzione esponenziale come somma di una funzione pari e di una dispari. Per le derivate e gli sviluppi in serie di Maclaurin si vedano le rispettive tavole.
La curva di equazione y = cosh(x) è detta → catenaria, perché rappresenta la configurazione di equilibrio di una catena, cioè di un filo omogeneo soggetto solo al proprio peso.
