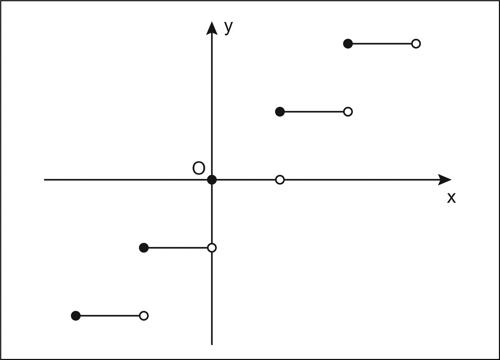
funzione parte intera

funzione parte intera

funzione parte intera o funzione pavimento o funzione floor, funzione di variabile reale, indicata con y = [x] oppure con y = ⌊x⌋ o con int(x), che associa a ogni numero reale x la sua parte intera, cioè il più grande numero intero che non supera x. Per esempio, [π] = 3, [2] = 2, [−π] = −4. È una funzione monotona crescente, di immagine Z, ed è costante in ogni intervallo della forma [n, n + 1), dove n è un qualsiasi numero intero: il suo grafico ha dunque il tipico aspetto a gradini. Si noti che [−x] non è in genere uguale a −[x], ma risulta, se x ∉ Z, [−x] = −[x] − 1. La funzione parte intera è una funzione continua a tratti, essendo continua in RZ, e presentando un salto di altezza 1 in ogni x ∈ Z, dove è continua da destra. Essa non è continua, ma è semicontinua a destra.

Per analogia con la funzione parte intera, si definisce anche la funzione parte intera superiore (detta anche funzione soffitto o funzione ceiling), indicata con y = ⌈x⌉, che associa a ogni numero reale la sua parte intera superiore, cioè il più piccolo numero intero maggiore o uguale a x. Risulta in genere: ⌈x⌉ = −⌊−x⌋ = ⌊x⌋ + 1, salvo che ⌈x⌉ = ⌊x⌋ se x ∈ Z.