funzione polinomiale
funzione polinomiale
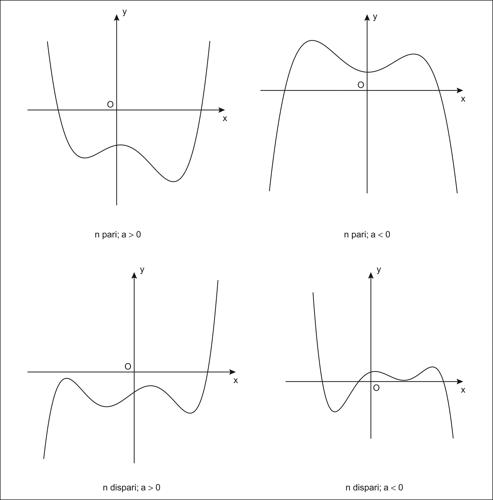
funzione polinomiale funzione la cui espressione algebrica è un polinomio. Si tratta di una funzione razionale intera. Una funzione polinomiale è definita ∀x ∈ R; il suo grado è dato dal grado del polinomio. Una funzione polinomiale di grado n ha al più n − 1 punti stazionari (dove la tangente al grafico della curva è parallela all’asse delle ascisse). Il comportamento all’infinito di una funzione polinomiale è diverso a seconda che il grado del polinomio sia pari o dispari. Poiché, infatti, è sempre possibile riscrivere il polinomio in x ponendo in evidenza il termine di grado massimo xn
dove q indica genericamente il termine noto, i termini frazionari in parentesi tendono a 0 al tendere di x all’infinito e l’espressione in parentesi tende al valore di a. Si hanno allora due possibilità:
• se n è pari, il valore di xn è sempre positivo e la funzione tende a +∞ o a −∞ a seconda del segno di a;
• se n è dispari, il valore assoluto di xn tende a ∞, ma la funzione tenderà a +∞ o a −∞ a seconda che x tenda a +∞ o a ‒∞; moltiplicando il valore di xn per a, che può essere positivo o negativo, si ottiene che la funzione può tendere all’infinito per valori positivi o per valori negativi. Il suo andamento grafico, a meno di punti di massimo e di minimo relativi intermedi, è crescente o decrescente.
Gli zeri reali di una funzione polinomiale sono al più n, ognuno considerato con la sua molteplicità (→ algebra, teorema fondamentale dell’).