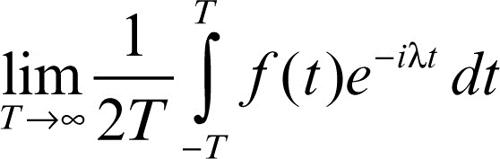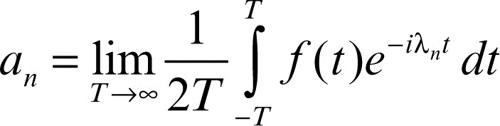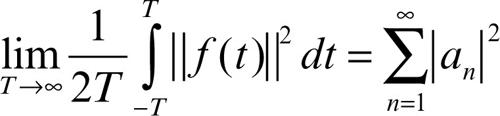funzione quasi-periodica

funzione quasi-periodica

funzione quasi-periodica funzione ƒ: R → R per la quale ∀ε > 0 esiste un insieme {τ}_ε ⊆ R relativamente denso tale che ∀τ ∈ {τ}_ε risulta

Per insieme relativamente denso si intende un insieme tale che esiste un numero l, detto lunghezza di inclusione, per cui in ogni intervallo [a, a + l] cade almeno un suo elemento.

Ogni valore di τ ∈ {τ}_ε si dice un ε-quasi periodo per ƒ: la differenza dei valori di ƒ nei punti di ascissa t e t + τ infatti non è 0, ma è comunque “piccola” al variare di t in R. Naturalmente, gli ε-quasi periodi diventano sempre più lunghi al tendere di ε a 0. La somma di due funzioni continue e periodiche con periodi incommensurabili non è per esempio una funzione periodica, bensì quasi-periodica.

Si dimostra che se ƒ è una funzione quasi-periodica, il limite

vale 0, tranne al più per una successione {λ_n} di valori, detti esponenti caratteristici di ƒ. Tale successione {λ_n} costituisce lo spettro della funzione quasi-periodica ƒ. Posto

si può associare a ƒ lo sviluppo

che costituisce una generalizzazione della serie di Fourier. Da questo sviluppo, con un procedimento che generalizza quello di Fejér per le serie di Fourier classiche, si può ottenere una successione di polinomi trigonometrici che converge uniformemente a ƒ in tutto R.

La nozione di funzione quasi-periodica si estende a funzioni ƒ: R → X, con X spazio di Banach, sostituendo il modulo con la norma. Se in particolare X è uno spazio di Hilbert, vale l’uguaglianza di Parseval nella forma

(→ Parseval, identità di).