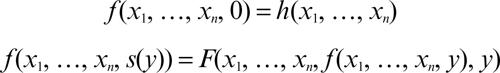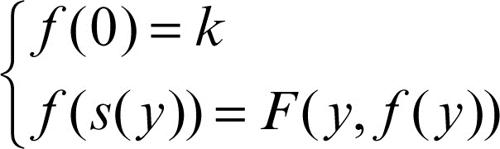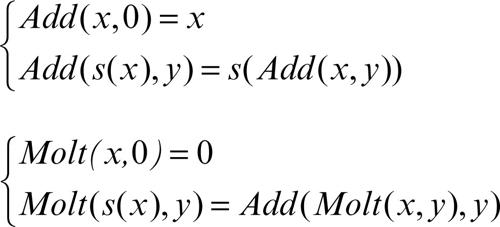funzione ricorsiva

funzione ricorsiva

funzione ricorsiva in logica, funzione aritmetica, cioè di dominio e codominio N, definita a partire da alcune funzioni base e attraverso alcune regole costruttive che ne garantiscono la → calcolabilità. La loro importanza è notevole proprio perché l’insieme delle funzioni ricorsive coincide con quello delle → funzioni calcolabili (è questo il contenuto della cosiddetta tesi di → Church). Le funzioni iniziali o di base da cui si parte sono:

• la funzione zero o funzione annullatore, che associa a ogni numero naturale il numero 0 ed è indicata simbolicamente con Z(x) (si legge «Z di x»). Si ha quindi Z(x) = 0 per ogni numero naturale x;

• la funzione successore, che associa a ogni numero naturale il suo successore ed è indicata con s(x); si ha quindi s(x) = x + 1 per ogni numero naturale x;

• le funzioni di proiezione o funzioni proiettore che associano a ogni ennupla ordinata di numeri naturali (x₁, x₂, ..., x_n) l’i-esimo numero, dove può variare da 1 a n. Si hanno quindi la proiezione

la proiezione

e, in generale,

Per definizione sono funzioni ricorsive tutte e sole le precedenti e tutte quelle che si ottengono da esse mediante l’applicazione di tre regole di formazione: schema della composizione, schema della ricorsione e schema della minimalizzazione.

• Schema della composizione: consiste nel formare una nuova funzione tramite la composizione di due o più funzioni ricorsive. Così, se g e h sono due funzioni ricorsive, anche

è una funzione ricorsiva. Più precisamente, se g è una funzione ricorsiva di m argomenti (funzione m-aria) e h₁ h₂, ..., h_m sono m funzioni ricorsive n arie, la funzione

è ricorsiva.

• Schema della ricorsione: consiste nel formare una nuova funzione ricorsiva di n + 1 argomenti ƒ(x₁, ..., x_n, y) a partire da una funzione ricorsiva di n argomenti h(x₁, ..., x_n) e da una funzione ricorsiva di n + 2 argomenti F(x_1, ..., x_n, z, y) secondo il seguente procedimento costruttivo:

Ciò significa che la funzione F permette di calcolare il valore della funzione ƒ in corrispondenza di un certo valore della variabile y a partire dal valore che essa assume in corrispondenza del valore precedente di y.

È possibile completare la definizione nel caso n = 0 a partire da un numero naturale assegnato k e una funzione ricorsiva F di due argomenti in questo modo:

Le funzioni ottenute dalle funzioni base applicando solo gli schemi di composizione e ricorsione, sono dette funzioni ricorsive primitive. Esempi di funzioni ricorsive primitive sono l’addizione e la moltiplicazione fra numeri naturali, che si possono indicare rispettivamente con Add(x, y) e con Molt(x, y) e che così sono definite con lo schema della ricorsione:

L’insieme delle funzioni ricorsive primitive comprende la maggior parte delle funzioni calcolabili con cui si opera usualmente, tuttavia non tutte le funzioni aritmetiche calcolabili possono essere espresse tramite i due schemi precedenti. Un esempio di funzione che non può essere costruita in questo modo è la funzione di → Ackermann, scoperta nel 1928. Esistono quindi funzioni ricorsive che non sono primitive; per considerarle tutte occorre pertanto aggiungere un ulteriore schema, lo schema della minimalizzazione.

• Schema della minimalizzazione: consiste nel formare una funzione a partire da una funzione ricorsiva per mezzo dell’applicazione dell’operatore di minimalizzazione o µ-operatore. Data una funzione ricorsiva di n + 1 variabili

tale che per ogni n-pla (x₁, x₂, ..., x_n) esista un numero y che verifichi l’uguaglianza

e indicato con

il più piccolo numero naturale y tale che

allora risulta definita una funzione ricorsiva ƒ di n variabili, nel seguente modo:

Il concetto di funzione ricorsiva venne introdotto negli anni Trenta del xx secolo allo scopo di delimitare, in termini matematicamente rigorosi, la classe delle funzioni di numeri naturali computabili algoritmicamente (→ calcolabilità). Furono proposte varie definizioni alternative: in termini di sistemi di equazioni (K. Gӧdel, S.C. Kleene), di lambda-definibilità (A. Church), di automi ideali (A.M. Turing) ecc. L’equivalenza dei diversi approcci venne interpretata come una prova del fatto che essi fornivano davvero una caratterizzazione adeguata della nozione informale di “funzione effettivamente computabile”. Questa convinzione fu codificata nella cosiddetta «tesi di Church», della quale non è possibile dare, in linea di principio, una dimostrazione rigorosa, e che tuttavia è dotata di una innegabile plausibilità.