fuoco
fuoco
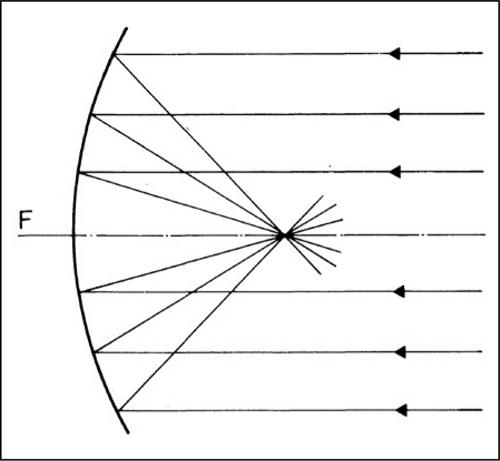
fuoco in geometria piana, particolare punto riferito a una → conica usato per definire la conica stessa. Ogni conica, infatti, può essere definita come luogo geometrico dei punti tali che il rapporto delle loro distanze da un punto fisso detto fuoco e da una retta fissa detta direttrice abbia un valore costante e (detto eccentricità). La polare di un fuoco è la direttrice associata a quel fuoco. Una conica possiede al più due fuochi reali. L’ellisse ha due fuochi reali sull’asse maggiore e due fuochi immaginari sull’asse minore, l’iperbole ha due fuochi reali su un asse e due fuochi immaginari sull’altro, la parabola ha un fuoco reale sul suo asse, mentre nella circonferenza tutti i fuochi coincidono con il centro. Un fuoco di una conica è il centro di un fascio di rette che si corrispondono in una involuzione ortogonale. Proprio a questa proprietà geometrica risale l’origine del termine: in una parete riflettente a forma di parabola tutti i raggi paralleli all’asse della parabola si riflettono in raggi passanti per il fuoco della parabola e dunque se si orienta uno specchio parabolico (cioè a sezione parabolica, → paraboloide) verso il sole tutti i raggi solari si riflettono concentrandosi in quel solo punto in cui, se vi si pone un oggetto combustibile, questo prende, appunto, fuoco; tali specchi sono detti specchi ustori e in questo modo, secondo una nota leggenda, Archimede contribuì alla difesa della città di Siracusa dall’assedio della flotta romana, incendiandone più navi. Per lo stesso motivo, si utilizzano antenne a forma parabolica per concentrare in un solo punto le onde elettromagnetiche. Si parla di fuoco anche nella geometria solida in relazione a solidi derivabili dalle coniche (paraboloide, ellissoide ecc.).
In geometria analitica, si individuano le coordinate dei fuochi di ciascuna conica a partire dalle rispettive equazioni delle coniche in forma canonica. L’ellisse di equazione canonica
(con a > b) ha due fuochi reali di coordinate:
In particolare, se l’ellisse è una circonferenza, i due fuochi coincidono nel centro della circonferenza, che nel caso considerato si identifica con l’origine degli assi cartesiani.
L’iperbole di equazione canonica
ha due fuochi reali di coordinate:
La parabola in forma canonica ha equazione y = ax 2 e il suo fuoco reale proprio F ha coordinate:
Traslando la parabola si ottiene il caso più generale di parabola ad asse parallelo all’asse delle ordinate, di equazione y = ax 2 + bx + c; il suo fuoco reale proprio ha coordinate
essendo ∆ = b2 − 4ac il discriminante del trinomio ax 2 + bx + c. L’altro fuoco è il punto improprio corrispondente alla direzione dell’asse della parabola.