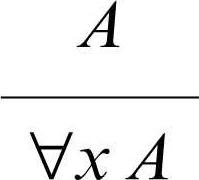generalizzazione

generalizzazione

generalizzazione una delle regole di → inferenza su cui si basa il concetto di deduzione formale nell'ambito di un sistema logico. In particolare, la regola di generalizzazione è presente nel calcolo dei predicati e permette l’introduzione del quantificatore universale, indicato con il simbolo ∀ (si legge «per ogni»), in una formula A nel modo seguente

dove la linea orizzontale separa la premessa A dalla conclusione ∀x A (si legge «per ogni x A»).

Grazie alla regola di generalizzazione è possibile passare da una formula ben formata A che esprime una proprietà relativa alle variabili che in essa compaiono, alla formula ben formata ∀x A che afferma che per ogni variabile x vale la proprietà A. Per esempio, si consideri in N il predicato P «essere un numero primo» e il predicato Q «essere multiplo di 4». Si consideri poi la forma predicativa vera corrispondente alla frase «se x è un numero primo allora x non è multiplo di 4»: P(x) ⇒ ￢Q(x). In base alla regola di generalizzazione è possibile dedurre dalla formula P(x) ⇒ ￢Q(x) la formula ∀x P(x) ⇒ ￢Q(x) per la quale «dato un qualunque numero x si ha che, se x è primo, allora x non è multiplo di 4».