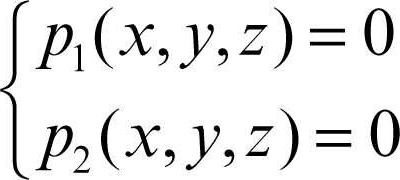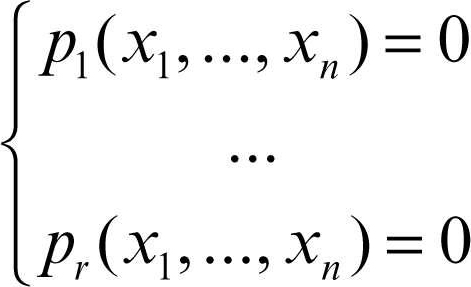geometria algebrica

geometria algebrica

geometria algebrica variante moderna e più astratta della geometria analitica; dato il peso prevalente assegnato alle strutture algebriche (quali, in particolare, anelli, campi e ideali), si può considerare più una branca dell’algebra che della geometria stessa, pur non perdendo di vista gli oggetti geometrici da cui trae origine. A partire da problemi riguardanti la forma e le intersezioni di curve e superfici, in geometria algebrica sono state utilizzate ed elaborate in misura crescente tecniche appartenenti ad altri ambiti della matematica.

La geometria algebrica nasce come studio di curve algebriche del piano o di curve e superfici algebriche dello spazio. Una curva algebrica nel piano affine reale è il luogo dei punti le cui coordinate sono soluzione di un’equazione polinomiale p(x, y) = 0 a coefficienti reali; tali sono per esempio le rette e le coniche, per le quali il polinomio p è rispettivamente di primo e di secondo grado. Una superficie algebrica nello spazio affine tridimensionale reale è il luogo dei punti le cui coordinate sono soluzione di un’equazione polinomiale p(x, y, z) = 0 a coefficienti reali; tali sono per esempio i piani e le quadriche, per le quali il polinomio p è rispettivamente di primo e di secondo grado. Una curva algebrica nello spazio affine tridimensionale reale è invece il luogo dei punti le cui coordinate sono soluzione di un sistema di due equazioni indipendenti:

in cui p₁ e p₂ sono due polinomi a coefficienti reali; tale è per esempio una retta nello spazio se p₁ e p₂ sono polinomi di primo grado che rappresentano due piani non paralleli, di cui il sistema è l’intersezione.

A partire da questi oggetti originari (curve e superfici, nel piano o nello spazio) strettamente collegati a oggetti geometrici disegnabili o quanto meno visibili, la geometria algebrica, a partire dal xix secolo, ha considerato oggetti sempre più generali e la generalizzazione è avvenuta in più direzioni.

Innanzitutto, anziché le sole soluzioni reali, si sono considerate anche le soluzioni nel campo C dei numeri complessi, sicché, per esempio, anche l’equazione polinomiale x ² + y ² + 1 = 0, che non ha alcuna soluzione reale, rappresenta in C una curva algebrica. Un altro tipo di generalizzazione si è avuta passando a considerare anche i “punti all’infinito” di tali curve e superfici, ambientandole cioè in uno spazio proiettivo e, comunque, nell’ambito della → geometria proiettiva: accanto alle curve e alle superfici algebriche affini si considerano così anche curve e superfici algebriche proiettive, vale a dire definite come il luogo dei punti in uno spazio proiettivo le cui coordinate omogenee sono soluzione di una o più equazioni polinomiali omogenee. Ogni curva o superficie algebrica affine può essere “completata” da una curva o superficie algebrica proiettiva, considerando il luogo delle soluzioni dei relativi polinomi resi omogenei.

Già queste generalizzazioni, soprattutto per impulso della cosiddetta scuola italiana di geometria algebrica (i cui principali esponenti furono G. Castelnuovo, F. Enriques e F. Severi), avevano portato, a cavallo tra il xix e il xx secolo, al concetto unificante di → varietà algebrica, che riassumeva in sé quelli di curva algebrica (varietà algebrica di dimensione 1, affine o proiettiva) e di superficie algebrica (varietà algebrica di dimensione 2, affine o proiettiva). Un’ulteriore generalizzazione si è avuta infine nella prima metà del xx secolo, quando si è constatato l’interesse di non limitarsi più soltanto al campo dei numeri reali o dei numeri complessi, ma anche a campi diversi, anche non algebricamente chiusi e finiti. In termini generali, si può dunque affermare che la geometria algebrica è quella parte della matematica che studia le configurazioni formate dagli zeri comuni a una famiglia di uno o più polinomi a n variabili e a coefficienti definiti su un campo. Se i polinomi sono tutti di primo grado, lo studio di tali sistemi rientra nel campo dell’→ algebra lineare. Se uno o più polinomi sono di grado n ≥ 2, occorre poi introdurre altre restrizioni, relative alla irriducibilità dei polinomi considerati. Infatti, se si considera per esempio il polinomio x ² − y, esso è irriducibile in R e i suoi zeri reali descrivono una parabola (che ben a ragione può definirsi una curva e, più in generale, una varietà algebrica affine; vedi fig. 1). Se invece si considera il polinomio x ² − y ², esso non è irriducibile perché può scomporsi come (x − y)(x + y) e conseguentemente i suoi zeri reali descrivono ciò che, da un punto di vista intuitivo, non è una curva, ma l’unione di due distinte curve (vedi fig. 2).

Gli importanti risultati di studio e classificazione di curve e superfici, ottenuti in ambito italiano, acuti, localmente rigorosi e fortemente ancorati a tematiche e problemi innegabilmente di carattere geometrico, mantenevano tuttavia un carattere di disorganicità e segnalavano l’esigenza di un inquadramento teorico più generale, per il quale si rendevano necessari strumenti algebrici opportuni e un nuovo linguaggio. Ciò avvenne a partire dagli anni Cinquanta del Novecento, principalmente in Francia, soprattutto sotto la spinta del bourbakismo e del poderoso cambio di impostazione, in senso strutturalista e su basi algebriche, avviato da questo movimento, che ha radicalmente cambiato il linguaggio per descrivere i tradizionali oggetti geometrici, in qualche modo modificandone così la natura. In ogni caso, poiché i polinomi (dei cui zeri, anche tradizionalmente, si interessa la geometria algebrica) hanno la struttura algebrica di un anello, era piuttosto naturale l’impatto con la nuova sistemazione algebrica. Si affermano quindi nuovi punti di vista: nel 1946 A. Weil introduce le varietà algebriche astratte, svincolando così le varietà algebriche dalla loro immersione in spazi algebrici o proiettivi. Successivamente, A. Grothendieck generalizza ulteriormente il concetto di varietà algebrica con la sua teoria degli schemi (→ schema).

Esaminando per linee generali come si sia sviluppato questo cambio di prospettiva e generalizzando quanto detto in precedenza, si può affermare che l’oggetto di studio della geometria algebrica è l’insieme delle soluzioni di un sistema di equazioni polinomiali a coefficienti in un campo K:

Se I = (p₁, ..., p_r) è l’ideale generato da p₁(x₁, …, x_n), …, p_r(x₁, ..., x_n) nell’anello dei polinomi K[x₁, …, x_n], allora l’insieme degli zeri comuni degli elementi di I coincide con quello dei suoi generatori; d’altra parte K[x₁, ..., x_n], è un anello noetheriano (→ Hilbert, teorema della base di), vale a dire un anello tale che ogni suo ideale è finitamente generato. Pertanto, più in generale, si considera come oggetto di studio della geometria algebrica un insieme algebrico, definito come l’insieme degli zeri comuni di un opportuno ideale / ⊆ K[x₁, …, x_n] nello spazio affine n-dimensionale su K, Aⁿ(K); tale insieme algebrico, definito a partire da /, è solitamente indicato con il simbolo V(l). Si dimostra che gli insiemi algebrici soddisfano le seguenti proprietà:

• l’unione di un numero finito di insiemi algebrici è un insieme algebrico;

• l’intersezione di una famiglia qualunque di insiemi algebrici è un insieme algebrico;

• l’insieme vuoto (definito dall’equazione 1 = 0) e tutto lo spazio (definito dall’equazione 0 = 0) sono insiemi algebrici.

Gli insiemi algebrici soddisfano quindi le caratteristiche dei chiusi di una topologia sullo spazio affine n-dimensionale, detta topologia di Zariski. Se K è un campo algebricamente chiuso (motivo per cui solitamente si assume che tale sia il campo di definizione di una varietà algebrica), è possibile stabilire una corrispondenza biunivoca fondamentale tra gli insiemi algebrici di Aⁿ e una particolare classe di ideali di K[x₁, ..., x_n]. A ogni ideale / di K[x₁, ..., x_n] è infatti associato l’insieme algebrico V(I) ⊆ Aⁿ; tale corrispondenza può essere invertita associando a ogni insieme algebrico Z ⊆ Aⁿ l’ideale ℑ(Z) di K[x₁, ..., x_n] costituito dai polinomi che si annullano su Z. Mentre però è vero che V(ℑ(Z)) = Z, è falso il viceversa: ℑ(V(/)) coincide infatti con Rad(I), l’ideale radicale dell’ideale I (→ Hilbert, teorema degli zeri di; → varietà). D’altra parte, un ideale e il suo ideale radicale definiscono sempre lo stesso insieme algebrico, vale a dire V(I) = V(Rad(/)); pertanto se ci si restringe a considerare gli ideali radicali, si ottiene una corrispondenza biunivoca (che inverte le inclusioni) tra insiemi algebrici di Aⁿ e ideali radicali di K[x₁, ..., x_n]. Secondo tale corrispondenza, i punti di Aⁿ corrispondono con gli ideali massimali di K[x₁, ..., x_n].

Un insieme algebrico Z = V(I) si dice irriducibile se l’ideale I che lo definisce è primo; da un punto di vista geometrico ciò equivale a richiedere che non esistano due chiusi Z₁, Z₂ contenuti strettamente in Z tali che Z = Z₁ ∩ Z₂. Per esempio, nel caso in cui Z è una curva nel piano affine definita da un’equazione p(x, y) = 0, l’irriducibilità equivale ad affermare che p(x, y) è un polinomio irriducibile. Una varietà (algebrica) affine è un insieme algebrico irriducibile Z contenuto in un opportuno spazio affine Aⁿ(K).

Se è data una varietà algebrica affine X = V(I) ⊆ Aⁿ definita su un campo K algebricamente chiuso, allora si definisce il suo anello delle coordinate, indicato con il simbolo K[X], come l’anello quoziente K[x₁, ..., x_n]/I i cui elementi sono le funzioni regolari su X: in virtù del teorema degli zeri di Hilbert, è allora possibile identificare i punti che compongono X con gli ideali massimali dell’anello delle coordinate K[X]. Si definisce infine il campo delle funzioni razionali su X come il campo dei quozienti dell’anello delle coordinate K[X].

Similmente a quanto fatto nel caso dello spazio affine, è possibile definire un’analoga topologia di Zariski anche nello spazio proiettivo Pⁿ(K); i chiusi irriducibili di tale topologia costituiscono le varietà (algebriche) proiettive.

A ogni punto p di una varietà algebrica X si può associare l’anello dei germi delle funzioni razionali su X definite in p (→ germe); poiché tale anello possiede un unico ideale massimale, esso è un anello locale. Poiché ogni varietà proiettiva Z può essere ricoperta con un numero finito di aperti affini (vale a dire di aperti i quali, dotati della topologia indotta dal loro ambiente Z, sono a loro volta varietà affini), in questo modo a ogni punto p di una varietà algebrica X (affine o proiettiva) è possibile associare un anello locale A_p. In tale anello locale è codificata la geometria della varietà X intorno al punto considerato: per esempio, in base alla struttura di A_p, è possibile stabilire se un punto p sia singolare o meno (→ punto singolare). Per esempio, se X è una curva, allora p è un punto non singolare se e solo se l’anello locale A_p è un dominio a fattorizzazione unica. Più in generale, la proprietà di un punto p di una varietà algebrica di essere non singolare equivale a una proprietà algebrica del suo anello locale A_p che va sotto il nome di regolarità e che in questo ambito non è possibile chiarire ulteriormente.

Si introduce pertanto il cosiddetto fascio strutturale O_X di una varietà algebrica X, definito come il fascio che associa a ogni aperto (di Zariski) U ⊆ X l’anello O_X(U) costituito dalle funzioni razionali su X che sono definite in ogni punto di U. Dato un punto p di X, tramite un’operazione di limite a partire dal fascio strutturale O_X è possibile definire un insieme limite di funzioni O_X,p, detto la spiga di X in p, ottenuto considerando il “limite” degli anelli O_X(U) al variare di U tra tutti gli aperti di X contenenti p: tale anello coincide con l’anello locale A_p sopra definito, costituito dai germi di funzioni razionali definiti in p. Il fascio strutturale di una varietà algebrica X si presenta dunque in modo naturale come lo strumento fondamentale per lo studio delle proprietà geometriche locali di X.

Avendo dotato ogni varietà algebrica del suo fascio strutturale, una generalizzazione naturale del concetto di varietà algebrica è quella di spazio localmente anellato: tale è uno spazio topologico X dotato di un fascio di anelli commutativi unitari O_X le cui spighe sono anelli locali; solitamente ci si riferisce a un tale spazio come a una coppia della forma (X, O_X).

Con Grothendieck si afferma infine la nozione di schema, oggetto d’importanza centrale nello sviluppo della geometria algebrica nella seconda metà del xx secolo e che generalizza il concetto di varietà. Uno schema affine è uno spazio localmente anellato (X, O_X) isomorfo (come spazio localmente anellato) allo → spettro di un anello commutativo unitario A, dotato del suo fascio strutturale: ciò vuol dire che, a meno di isomorfismi, si può assumere X = Spec(A) e O_X = O_A; uno schema è invece uno spazio localmente anellato in cui per ogni punto esiste un aperto U che come spazio localmente anellato, dotato del fascio O_X|_U, restrizione a U del fascio O_X, è uno schema affine.

lettG_00590.rtf