geometria analitica

geometria analitica

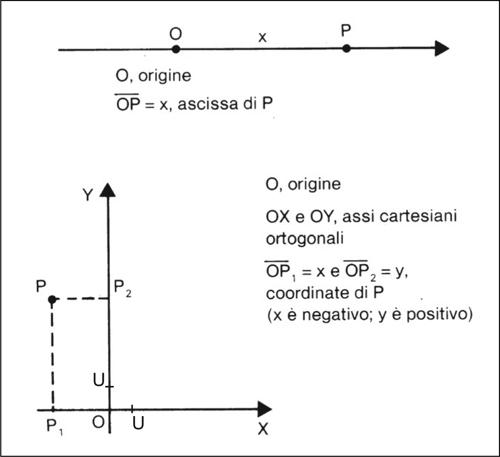
geometria analitica studio degli oggetti e delle relazioni della geometria attraverso l’utilizzo di metodi e strumenti algebrici o, più in generale, analitici, ottenuto tramite l’introduzione di coordinate, e, viceversa, la rappresentazione grafica di relazioni algebriche. L’essenza della geometria analitica consiste nel porre un ambiente geometrico in corrispondenza con un insieme numerico e nel tradurre sistematicamente questioni geometriche in questioni analitiche e viceversa. In tale modo, ai ragionamenti dimostrativi e costruttivi tipici della → geometria sintetica, cui in qualche modo si contrappone, si sostituiscono o si affiancano procedure di calcolo algebriche così che per la soluzione di un problema si utilizzano sia le risorse della geometria sia quelle dell’algebra e dell’analisi. Tale scopo è raggiunto mediante l’introduzione di un sistema di riferimento, detto riferimento cartesiano, che stabilisce una corrispondenza tra i punti di una retta, del piano o dello spazio e, rispettivamente, i numeri reali, le coppie ordinate di numeri reali e le terne ordinate di numeri reali (→ coordinate cartesiane). Sulla retta esso si ottiene fissando un punto O, detto origine del riferimento, e un punto unitario U. Il segmento OU rappresenta l’unità di misura, al punto O si attribuisce come ascissa il numero 0 e al punto U il numero 1. Ogni punto P della retta sarà allora individuato da un numero (la sua ascissa) dato dal rapporto tra OP e OU preso con segno positivo o negativo a seconda che P stia dalla stessa parte di U rispetto a O o dalla parte opposta. Nel piano, un sistema di riferimento Oxy si ottiene considerando due rette indicate con x e y, dette assi, orientate e dotate di unità di misura, tra loro perpendicolari e che si intersecano in un punto O, detto origine del riferimento. L’asse x è detto asse delle ascisse, l’asse y è detto asse delle ordinate. Le coordinate di un punto P del piano si ottengono considerando l’ascissa del punto P_x (ottenuto intersecando la retta per P parallela all’asse y con l’asse x) e quella del punto P_y (ottenuto intersecando la retta per P parallela all’asse x con l’asse y). Ogni punto P del piano è in questo modo individuato da una coppia ordinata di numeri reali, le sue coordinate, e si scrive P(x, y): il numero x è detto ascissa del punto P, il numero y è detto ordinata. Con tale sistema di riferimento cartesiano Oxy si stabilisce la corrispondenza biunivoca tra punti del piano e coppie di numeri reali (x, y), essendo il primo un insieme di oggetti geometrici e il secondo un insieme di oggetti numerici. Un piano in cui sia stato definito un sistema di riferimento cartesiano è, per brevità, detto piano cartesiano.

A partire da tale corrispondenza se ne stabiliscono nel piano molte altre tra classi di oggetti geometrici e classi di oggetti algebrici, quali per esempio:

• rette ↔ equazioni di primo grado;

• coniche ↔ equazioni di secondo grado.

Anche le relazioni tra gli oggetti geometrici possono così tradursi in relazioni numeriche o algebriche e lo studio dei fatti geometrici può ricondursi al calcolo algebrico che, in quanto tale, è dotato di una maggiore automaticità di procedimento.

Per esempio, due rette non parallele all’asse delle ordinate sono tra loro parallele (relazione geometrica) se nelle corrispondenti equazioni, y = m₁x + q₁ e y = m₂x + q₂, sono uguali i loro coefficienti angolari: m₁ = m₂ (relazione algebrica); due rette, di equazioni y = m₁x + q₁ e y = m₃x + q₃ sono invece perpendicolari (relazione geometrica) se i loro coefficienti angolari sono l’uno l’inverso dell’opposto dell’altro: m₃ = −1/m₁ (relazione algebrica). Stabilito ciò, la proposizione che due rette perpendicolari alla stessa retta sono tra loro parallele può essere dimostrata con metodo analitico (o con procedimento analitico) nel seguente modo:

In modo analogo (considerando tre rette tra loro perpendicolari convergenti in un unico punto origine O) si può considerare un sistema di riferimento Oxyz nello spazio tridimensionale e in esso a ogni punto corrisponde una terna ordinata di numeri reali (x, y, z).

È fondata consuetudine attribuire la nascita della geometria analitica a P. de Fermat e, in modo indipendente, a Cartesio, che espose il suo calcolo geometrico nel trattato sulla Geometria (1637), una delle appendici del Discorso sul metodo. Tuttavia, i diversi elementi che la caratterizzano sono presenti nella storia ben prima del xvii secolo. Per esempio, fin dai tempi più remoti le osservazioni astronomiche avevano condotto a utilizzare un sistema di coordinate per identificare la posizione di una stella – l’angolo rispetto all’orizzonte e l’angolo rispetto alla direzione nord (detti rispettivamente altezza e azimut nel cosiddetto sistema altazimutale di riferimento) –, ma tale metodo non era stato messo in relazione con altri fatti geometrici. Analogamente, lo studio di curve attraverso relazioni di tipo algebrico era già stato avviato nell’antica Grecia, nel iii secolo a.C., con Archimede e, soprattutto, Apollonio di Perge, che descrive le coniche a partire dai loro diametri. Anche la rappresentazione grafica di un fenomeno aveva degli illustri precursori: all’anno Mille circa risale infatti l’invenzione, da parte di Guido d’Arezzo, del tetragramma (poi diventato pentagramma) per descrivere la successione delle note, con la loro diversa altezza, allo scorrere del tempo. Indubbiamente, però, è con Fermat e Cartesio che i diversi aspetti trovano un consapevole punto di sintesi, anche perché nel frattempo si erano affermati e consolidati molti simbolismi e regole propri del linguaggio algebrico; tuttavia, ancora in Cartesio è fissato, nel piano, uno solo degli assi e si considerano soltanto coordinate non negative. Il metodo è poi alla base dello sviluppo del calcolo infinitesimale, dovuto a I. Newton e G.W Leibniz, in quanto rende familiare, negli ambienti matematici e scientifici, la rappresentazione delle funzioni in un piano cartesiano e lo studio delle tangenti, delle normali e delle curvature dei rispettivi grafici. Il metodo delle coordinate ha in seguito condotto alla prassi di studiare le curve piane come gli insiemi delle soluzioni di corrispondenti equazioni in due variabili e, nel xvii secolo, con A. Clairaut ed Eulero, viene esteso allo spazio tridimensionale. Clairaut, in particolare, pubblica uno studio sulle curve a doppia curvatura ed Eulero determina l’equazione delle superfici di secondo grado. I metodi della geometria analitica sono poi stati generalizzati allo studio delle caratteristiche di spazi a quattro o a più dimensioni, non più rappresentabili compiutamente attraverso un disegno, ma tuttavia utili modelli per descrivere situazioni e risolvere problemi coinvolgenti anche più di tre variabili.