geometria descrittiva
geometria descrittiva
geometria descrittiva settore della geometria che studia i metodi per rappresentare su un piano gli oggetti dello spazio tridimensionale. La sua origine si deve far risalire agli studi rinascimentali sulla → prospettiva, anche se la sua principale sistemazione risale alla fine del xviii secolo ed è dovuta al matematico francese G. Monge. I metodi della geometria descrittiva si fondano su una serie di operazioni caratteristiche della → geometria proiettiva: proiezioni, sezioni e ribaltamenti. I principali sono: proiezioni ortogonali, proiezioni quotate e proiezioni centrali.
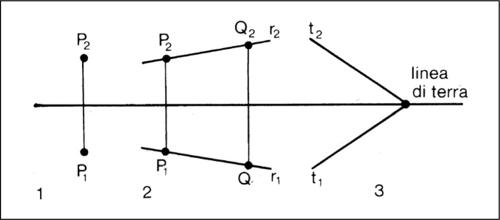
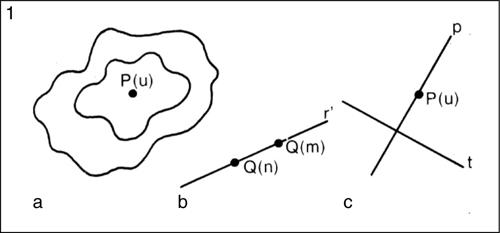
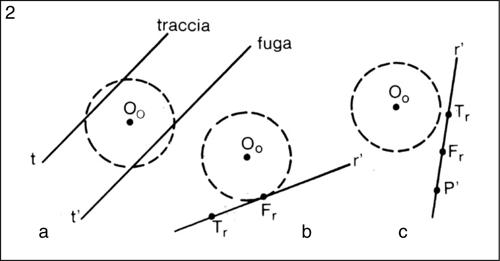
Nel metodo delle proiezioni ortogonali, detto anche metodo di Monge, si fissano due piani fra loro perpendicolari (piano orizzontale e piano verticale), che si intersecano secondo una retta detta linea di terra; per rappresentare una qualunque figura sul piano del disegno, ammettendo che questo coincida col piano orizzontale, si ribalta quello verticale intorno alla linea di terra. In taluni casi particolari, si introduce anche un terzo piano (piano di profilo), perpendicolare ai primi due. Le figure geometriche vengono rappresentate attraverso le proiezioni ortogonali dei loro punti (per esempio un cubo si rappresenta proiettando i sei vertici); una retta può essere rappresentata proiettando due suoi punti, o mediante le proiezioni ottenute con due piani passanti per essa (uno perpendicolare al piano orizzontale e uno perpendicolare al piano verticale); un piano si rappresenta mediante le due sezioni (tracce) col piano orizzontale e con quello verticale (nel caso di piani passanti per la linea di terra, si ricorre alla traccia sul piano di profilo). Mentre le proiezioni ortogonali sono particolarmente adatte alla rappresentazione di oggetti aventi le tre dimensioni spaziali dello stesso ordine di grandezza (edifici e oggetti dell’industria), le proiezioni quotate si adattano alla rappresentazione di figure in cui una dimensione è nettamente inferiore alle altre due: hanno avuto origine da studi di carattere topografico e sono un misto di rappresentazione proiettiva e analitica. Nel metodo delle proiezioni quotate un punto P è rappresentato, nel piano detto quadro, dal punto P′, sua proiezione ortogonale, e dalla sua quota, che è un numero scritto accanto a P′. Una retta r si rappresenta mediante la sua proiezione ortogonale r′ e con la quota di due suoi punti (scritta vicino alle loro proiezioni). Un piano si rappresenta mediante la sua intersezione col quadro (traccia) e con una retta di pendio sulla quale è segnata la quota unitaria del punto del piano che dista di 1 (nell’unità di misura scelta) dal quadro. Per la rappresentazione di oggetti di forma qualsiasi (per esempio i rilievi su una carta topografica) si usano le curve di livello, cioè le linee di intersezione di tali oggetti con piani paralleli al quadro e alle distanze uno, due, tre ecc. Nel metodo delle proiezioni centrali, a partire da un punto O (centro di proiezione) esterno a un piano, detto quadro, si tracciano le rette (raggi) passanti per i punti delle figure da rappresentare, prolungandole fino a intersecare il quadro e ottenendo su questo le immagini dei punti. Poiché tutti i punti da rappresentare incontrati da un raggio hanno la stessa immagine, questa non è sufficiente a definire un punto; si segna pertanto sul quadro il punto O0 (proiezione ortogonale di O sul quadro) e un cerchio di distanza di raggio uguale alla distanza OO0. Rette e piani costituenti le figure vengono poi rappresentati mediante le tracce (punti o rette, intersezioni effettive col quadro) e gli elementi (punti o rette) di fuga determinati da rette o piani passanti per O e paralleli a quelli dati. Questo tipo di proiezioni è strettamente connesso con la prospettiva e il disegno.