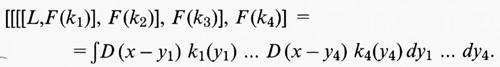Geometria non commutativa

Geometria non commutativa

Sommario: 1. Introduzione. 2. La meccanica quantistica e l'algebra degli operatori. 3. Le forme differenziali quantistiche. 4. Le C*-algebre e la loro teoria L₂. 5. Le W*-algebre e la loro teoria L₂. 6. I campi quantistici universali liberi. 7. Un esempio: le funzioni non lineari dell'equazione d'onda quantistica. 8. Il lemma di Poincaré infinito-dimensionale e la teoria quantistica dei campi multidimensionali. 9. Conclusione. □ Bibliografia.

1. Introduzione

La geometria non commutativa è un nuovo campo di studio emerso dall'analisi funzionale algebrica, originariamente sotto l'impulso della teoria quantistica, ma sviluppatosi in seguito in differenti direzioni. Si deve a John von Neumann, più che a chiunque altro, il merito di aver iniziato l'audace e in definitiva acuta linea di ricerca che ha fatto divenire la geometria non commutativa una realtà tecnica, anche se il contributo di Izrail′ Gel′fand e dei suoi collaboratori è risultato decisivo. In effetti, la differenza tra le due linee di sviluppo può essere essenzialmente considerata come quella tra le W*-algebre da una parte e le C*-algebre dall'altra, cioè una differenza fondamentale, e non meramente tecnica, tra particolari varietà di algebre degli operatori nello spazio di Hilbert.

Ciò che ha fornito l'incentivo principale sia a von Neumann all'inizio, sia all'innovazione attuale, è stata la sfida della teoria quantistica, la quale appare come una varietà naturale della geometria non commutativa. Oltre a rappresentare un valido strumento per chiarire e spiegare gli aspetti generali della teoria quantistica, la geometria non commutativa costituisce il presupposto per l'estensione della teoria quantistica rigorosa del campo non lineare a uno spazio-tempo quadridimensionale. Questo è stato uno dei problemi della fisica matematica più difficili da trattare e la sua parziale risoluzione, in un modo matematicamente coerente, ha per la prima volta fornito la dimostrazione che la teoria quantistica non lineare di campo in uno spazio-tempo quadridimensionale non è un'illusione come molti, dopo diversi decenni di stasi, cominciavano a sospettare, ma un soggetto affrontabile sia dal punto di vista logico che analitico.

La geometria non commutativa, inoltre, è maturata in parte dagli sviluppi verificatisi in topologia algebrica, come ad esempio l'efficace algebrizzazione della teoria omologica da parte di Samuel Eilenberg e Saunders MacLane; quest'ultima a sua volta ha ispirato la teoria coomologica generale di Gerhard Hochschild che forma la base concettuale per le estensioni nel campo della geometria non commutativa: estensioni piuttosto sofisticate e tecnicamente impegnative, alle quali i lavori di Alain Connes e di Gennadi Kasparov hanno contribuito in modo notevole. Comunque, probabilmente, resta da vedere se esse hanno implicazioni fondamentali per problemi al di fuori della matematica e questo articolo, quindi, si concentrerà essenzialmente sull'applicazione fondamentale della geometria non commutativa, cioè sulla teoria quantistica di campo non lineare.

2. La meccanica quantistica e l'algebra degli operatori

La geometria non commutativa deriva dall'analisi astratta, nata negli anni venti sulla base delle possibilità aperte dalla meccanica quantistica, possibilità delle quali si avvalsero in particolare von Neumann e Marshall Stone. Il teorema di Stone-von Neumann (1931), che ha specificato la struttura della rappresentazione unitaria generica delle relazioni di Weyl (v. cap. 4), stabilisce l'equivalenza tra i formalismi quantistici di Heisenberg e di Schrödinger. Le relazioni di Weyl sono un modo diverso di scrivere le relazioni di commutazione di Heisenberg. Precisamente, se p e q sono operatori corrispondenti alla quantità di moto e alla posizione, canonicamente coniugati, la corrispondente relazione di Weyl si scrive:

e^isp e^itq = e^ist e^itq e^isp,

in cui s e t sono numeri reali, peraltro arbitrari. Al contrario della corrispondente relazione di Heisenberg, questa formulazione fa intervenire soltanto operatori limitati. Il teorema di Stone-von Neumann è stato il primo teorema non banale di struttura per una rappresentazione unitaria infinito-dimensionale di un gruppo non commutativo e per tale ragione rappresenta un prototipo molto importante per la teoria infinito-dimensionale dei gruppi di Lie. Von Neumann comprese la grande importanza di questa teoria per la meccanica quantistica e sollecitò fortemente il suo amico e collega Eugene Wigner a sviluppare la teoria nel caso del gruppo di Poincaré. L'articolo pubblicato da Wigner su questo argomento (1940) è stato uno dei lavori più citati del XX secolo e tuttora i fisici vi fanno riferimento quasi con la reverenza dovuta a un testo sacro, malgrado esso fosse stato inizialmente rifiutato da una rivista di fisica e pubblicato in una rivista di matematica grazie ai buoni uffici di von Neumann.

Von Neumann stesso si assunse il compito ancor più impegnativo della razionalizzazione della fenomenologia quantistica, che sviluppò attivamente sia utilizzando i principî fondamentali della fisica, sia in una plausibile forma matematica. Assieme a Stone, egli aveva in precedenza enunciato nella sua forma definitiva il teorema spettrale nello spazio complesso di Hilbert e la teoria dell'estensione degli operatori hermitiani, sviluppando in tal modo fino ai massimi livelli il lavoro iniziato da Hilbert, la cui perspicacia nell'aver usato il termine ‛spettro' già vent'anni prima è tuttora degna di nota.

Von Neumann si rivolse quindi allo studio dei sistemi non commutativi di operatori nel contesto di uno spazio di Hilbert e in particolare iniziò il suo programma di ricerca su ciò che lui chiamò ‛anelli', oggi noti come W*-algebre. I suoi articoli su questi e su argomenti relativi costituiscono probabilmente il contributo più originale e importante alla matematica del XX secolo.

Nel frattempo, la crescente algebrizzazione dell'analisi funzionale, dovuta prevalentemente al lavoro di Frigyes Riesz e Stefan Banach, fu portata ai massimi livelli dai matematici sovietici, in particolare da Gel′fand, Mark Krein e Mark Naimark. La scoperta da parte di Gel′fand e di Andrej Kolmogorov (1939) che l'algebra C(G) delle funzioni continue a valori complessi su uno spazio compatto G determina lo spazio, in maniera puramente algebrica, non solo completò la linea di ricerca di Banach e Stone, ma servì anche a far notare che, in linea di principio, si potrebbe lavorare altrettanto bene con un'algebra funzionale appropriata quanto con uno spazio topologico. La prova era semplice, ma introdusse un potente strumento che era nuovo nel contesto dell'analisi funzionale, l'ideale massimale. Lo spazio di tutti gli ideali massimali in C(G), in cui è stata introdotta una topologia in maniera naturale dal punto di vista algebrico o, equivalentemente, lo spazio dei funzionali lineari moltiplicativi su C(G) nella loro (definibile algebricamente) W*-topologia, era omeomorfo a G. Infine, l'idea della geometria non commutativa divenne inevitabile, specialmente alla luce dell'articolo di von Neumann sul formalismo della meccanica quantistica, presentato nel 1936 alla conferenza di topologia di Mosca, e della successiva straordinaria caratterizzazione delle algebre degli operatori di uno spazio di Hilbert fatta da Gel′fand e Naimark.

Le proprietà dello spazio G potrebbero essere messe in relazione con le proprietà dell'algebra C(G), la quale, se sostituita da una opportuna algebra non commutativa, potrebbe essere utilizzata per descrivere un tipo di spazio virtuale corrispondente (simile a quello introdotto in seguito da George Mackey in relazione alla teoria ergodica), o un sistema quanto-meccanico. Le ragioni a sostegno di questa idea furono rafforzate dalla straordinaria semplicità della caratterizzazione di C(G) sviluppata dalla scuola di Gel′fand. Si dimostrò che ogni algebra di Banach A involutiva con una norma che soddisfi la condizione ∥aa*∥ = ∥a∥², dove ∥a∥ denota la norma dell'operatore a (v. operatori, teoria degli, vol. XI), è algebricamente isomorfa a C(G); inoltre, ciascun isomorfismo di questo tipo è automaticamente una isometria. Questo sorprendente risultato fornì un approccio semplice e dalle grandi potenzialità alla teoria spettrale nello spazio di Hilbert, poiché non fu difficile mostrare che l'algebra generata da ogni insieme commutante di operatori limitati autoaggiunti aveva queste proprietà.

Ancora più essenziale fu la scoperta, già accennata nel 1943 da Gel′fand e Naimark, di una caratterizzazione intrinseca puramente algebrica delle C*-algebre. Tale scoperta rappresentò uno spartiacque nella teoria generale delle algebre autoaggiunte; lo stesso von Neumann manifestò la sua sorpresa per l'inaspettata caratterizzazione degli operatori di uno spazio di Hilbert in maniera puramente algebrica. Già nella sopra ricordata conferenza di topologia del 1936, von Neumann, Stone e altri avevano presentato un lavoro che proponeva una visione dell'analisi funzionale più astratta e algebrica di quella allora corrente in Europa. I risultati ottenuti pochi anni dopo dai matematici sovietici erano in linea con quella impostazione, ma erano tecnicamente molto differenti e di grande originalità. Subito dopo ci si rese conto che le C*-algebre fornivano un linguaggio naturale per la fenomenologia quantistica, cioè per esprimere le relazioni fra osservabili, stati, spettri e il ruolo generale dei gruppi di invarianza, ecc.

3. Le forme differenziali quantistiche

Prima di entrare nei particolari degli sviluppi delle W*-algebre e delle C*-algebre, potrà essere utile chiarire che cosa sia la geometria non commutativa mediante un esempio di come essa può essere espressa in pratica. Una delle più semplici e più naturali esemplificazioni della geometria non commutativa è rappresentata sicuramente dal concetto e dalla teoria delle forme differenziali quantistiche, le quali non sono ottenute dalle forme differenziali classiche per mezzo di un processo di quantizzazione, ma rappresentano piuttosto un tipo più generale di oggetti; le forme differenziali quantistiche, infatti, da una parte includono le forme classiche come un sottosistema, e dall'altra si evolvono a partire dalla teoria quantistica.

Le forme quantistiche potrebbero essere introdotte in diversi contesti, come quello delle W*-algebre o quello delle C*-algebre, ma sarà più semplice e in definitiva più vicino al formalismo della teoria quantistica dei campi trattare queste forme in un contesto puramente algebrico. Indichiamo con L uno spazio complesso finito-dimensionale e con F una forma reale antisimmetrica non degenere su L. Sarà indicato con E(L) il quoziente tra l'algebra libera non commutativa (ma associativa) generata da L e l'ideale generato dalle relazioni [x,y]=(xy - yx)=F(x,y)e per x e y arbitrari in L, dove e è l'identità dell'algebra. E(L) è l'algebra infinitesimale di Weyl ed è isomorfo all'algebra generata dall'insieme di operatori canonici p₁, ..., p_n, e q₁, ..., q_n della meccanica quantistica, dove 2n è la dimensione di L, che soddisfano le relazioni di commutazione di Heisenberg,

[p_j, p_k] = 0, [q_j, q_k] = 0, [p_j, q_k] = - iδ_jk.

Notiamo che la moltiplicazione M_F per un polinomio F in q₁, ..., q_n soddisfa le semplici ‛relazioni di commutazione': [M_F, q_j] = 0, [M_F, p_j] = iM_Fj′, dove F_j′ = ∂F/∂q_j. Il differenziale dF = Σ_j (∂F/∂q_j) dq_j, di conseguenza, è esprimibile semplicemente in termini dei commutatori piuttosto che delle derivate. Una notevole proprietà delle relazioni di commutazione è che si applicano anche quando, al posto dell'operazione di moltiplicazione per un polinomio, è usato un operatore generico. Un'altra proprietà è che le relazioni di commutazione rappresentano tutto ciò che forma la materia della meccanica quantistica pratica. Gli operatori della meccanica quantistica sono in genere funzioni delle p e delle q che soddisfano le relazioni di Heisenberg o di Weyl e non esiste nessuna distinzione invariante tra le p da una parte e le q dall'altra. In una teoria relativistica, ad esempio, le p a un certo istante sono trasformate in funzioni delle p e delle q a un istante successivo. L'analisi di Fourier, inoltre, fornisce una motivazione per trattare le p e le q sullo stesso piano, come è stato spesso proposto su basi fisiche.

Per queste ragioni risulta naturale cercare di generalizzare il concetto di differenziale di una funzione, df = Σ_j (∂f/∂x_j) dx_j mediante una definizione del differenziale di un operatore A in termini dei commutatori, e ciò in effetti semplifica e generalizza il calcolo usuale delle forme. A questo fine una 0-forma quantistica (o Q-0 forma) è definita come un elemento di E(L) e una m-forma quantistica (o Q-m forma) è definita come un'applicazione alternante m-lineare da L a E(L). La derivata ∂K di una data Q-m forma K è allora naturalmente definita dall'equazione

dove la somma è estesa a tutte le permutazioni cicliche t degli interi 1, 2, ..., m, m+1 e sgn (t) è pari a + 1 per le permutazioni di tipo pari, e a - 1 per quelle di tipo dispari. Il prodotto di K per una Q-forma di grado n è definito in maniera simile.

Ne consegue quindi che la somma diretta su m di tutte le Q-m forme (identicamente nulle se m>2n) è un'algebra associativa; e se K è una Q-forma, allora lo è anche ∂K e ∂²K = 0. Se si definisce una Q-forma K come chiusa se ∂K=0 ed esatta quando K=∂H per una data Q-forma H, allora il lemma di Poincaré si estende come segue. Teorema: una Q-forma chiusa è esatta.

Inoltre, le forme differenziali convenzionali o C-forme, sono incluse come un sottosistema sul quale ∂ coincide effettivamente con d.

È interessante e importante per l'analisi dei campi di fermioni che la teoria si adatti completamente al caso di una forma simmetrica F, con la sostituzione delle relazioni di Weyl con quelle di Clifford. Il calcolo delle corrispondenti Q-forme simmetriche assomiglia qualitativamente a quello usato per le Q-forme antisimmetriche appena trattato, anche se è tecnicamente piuttosto differente. Vale ancora che le forme chiuse sono esatte e che le Q-forme costituiscono un'algebra associativa.

Più generalmente, F può essere la somma diretta di componenti simmetriche e antisimmetriche che corrispondono, in termini fisici, al prodotto tensoriale dei campi di bosoni e fermioni, dei quali ci occuperemo in seguito, su spazi finito-dimensionali di ‛particella-singola'. In tutti questi casi, la versione di Wick (‛ordinata') di un monomio u=z₁z₂ ... z_k in E(L), indicata usualmente con :u:, è definibile come un cociclo la cui esistenza è assicurata dal lemma di Poincaré.

Più specificatamente, la versione ‛rinormalizzata' N(u) di u relativa a un dato funzionale lineare e su E(L) è definita grazie alle condizioni di ricorrenza [N(u),z]=N([u,z]) per z arbitrario in L, assieme alla condizione di normalizzazione relativa al dato funzionale lineare e su E(L). Nel caso del prodotto di Wick, e è il ‛vuoto libero' (cioè l'autostato corrispondente al più piccolo autovalore dell'hamiltoniana libera), ma la teoria si applica ugualmente al vuoto fisico (definito dal più piccolo autovalore dell'hamiltoniana totale). Il caso - analiticamente molto più sofisticato - in cui L è infinito-dimensionale sarà trattato nel capitolo seguente.

4. Le C*-algebre e la loro teoria L₂

Uno dei principali obiettivi che von Neumann si poneva era quello di riuscire a ottenere uno schema matematico coerente e rigoroso per la fenomenologia quantistica. Il suo intervento alla conferenza di Mosca diede un contributo di grande interesse che influì in modo determinante nel correlare i fondamenti fisici e un modello matematico rigoroso, ma si basava sul punto di vista della W*-algebra. Egli pensava che i fisici fossero ‟nell'anello sbagliato", cioè la W*-algebra. Infatti, un candidato naturale per l'anello giusto, il suo famoso fattore ‛approssimatamente finito' di tipo II₁, in seguito ha avuto un ruolo basilare nella rappresentazione di campi di fermioni liberi. Ma la trattazione di campi interagenti ha richiesto uno sforzo molto maggiore sotto l'aspetto di nuove considerazioni qualitative.

La scoperta di Gel′fand e Naimark si basava sull'uso di funzionali lineari positivi, che erano stati precedentemente messi in evidenza da von Neumann in connessione con la fenomenologia quantistica ed erano stati studiati indipendentemente da Krein e dai suoi collaboratori in maniera tecnicamente incisiva. Negli anni quaranta fui colpito dalla complementarità tra il punto di vista applicato di von Neumann e quello puramente matematico di Gel′fand, Naimark e Krein. Il risultato fu una versione della fenomenologia quantistica di von Neumann basata tecnicamente sulla teoria della C*-algebra.

In questa teoria, le osservabili quantistiche sono rappresentate da elementi autoaggiunti dell'algebra sui quali gli stati sono funzionali lineari positivi e normalizzati. Gli stati puri sono punti estremi dell'insieme di tutti gli stati, essenzialmente come in una precedente formulazione di Hermann Weyl. La loro esistenza fu dimostrata dal teorema di Krein-Milman che, incidentalmente, fornì un modo per associare stati ben definiti a punti nello spettro continuo e non solamente nello spettro discreto dell'hamiltoniana. La dinamica quantistica divenne più comprensibile grazie alla rappresentazione per mezzo degli ‛automorfismi' dell'algebra delle osservabili, piuttosto che per mezzo di ‛gruppi unitari a un parametro', chiarendo problemi quali quello della consistenza fisica delle energie di punto-zero. Per correttezza va riconosciuto che questo punto di vista oggi non è più controverso, tra i fisici matematici, di quanto lo sia la geometria analitica.

Una C*-algebra è l'analogo non commutativo di uno spazio di funzioni continue, ma spesso nell'analisi funzionale un ruolo più fondamentale è svolto da uno spazio di Hilbert. Questo è l'analogo non commutativo dello spazio L₂, cioè lo spazio delle funzioni di quadrato sommabile, e nasce, per una data C*-algebra, nel contesto di un dato stato per l'algebra. Considerando per semplicità il caso di una C*-algebra C con identità 1, uno stato e è un funzionale lineare tale che e(SS*) ≥ 0 per tutte le S in C, e inoltre e(1)=1. Questo porta a una teoria di tipo L₂ se il prodotto interno 〈S,T〉 tra due elementi di C viene definito come e(T*S). Il completamento di C rispetto al suo prodotto interno è quindi uno spazio di Hilbert su cui C è rappresentata canonicamente tramite l'associazione di un arbitrario elemento R di C con l'operatore che trasforma la classe residua di S in C (modulo lo spazio degli operatori S con 〈S,S〉 = 0) nella classe residua di RS. Il risultato di questa cosiddetta ‛costruzione GNS' (Gel′fand, Naimark e Segal; v. operatori, teoria degli, vol. XI) è una teoria di tipo L₂ per le C*-algebre che fornisce un contesto di spazio di Hilbert indipendentemente dalla sua esistenza precedente e include la struttura nel formalismo delle W*-algebre.

Il formalismo delle C*-algebre conserva alcuni importanti vantaggi algebrici che in generale non si trasportano nel contesto delle W*-algebre. Tra le altre cose, ciò che è rilevante è la facilità con cui gli automorfismi della struttura di particella singola possono essere trasportati nell'algebra del campo quantistico, anche nel caso in cui L sia infinito-dimensionale. Considerando in particolare il caso di una forma antisimmetrica F, ogni trasformazione simplettica (cioè che conserva F) T su L induce un unico automorfismo dell'appropriata algebra di Weyl di ‛tipo finito'. Quest'ultima è definita come la chiusura, nella topologia uniforme dell'operatore, dell'unione delle W*-algebre generate dalle W(z), per z che varia su sottospazi finito-dimensionali di L. Qui si assume che le W(z) soddisfino le relazioni di Weyl nella forma più generale: W(z)W(z′) = exp [(1/2) iA(z,z′)] W(z + z′). La restrizione a sottospazi finito-dimensionali è essenziale per l'unicità della risultante C*-algebra, cioè per la sua indipendenza dalla rappresentazione delle relazioni di commutazione canoniche.

L'algebra di Weyl di tipo finito è un'eccezione tra le C*-algebre coinvolte nella teoria di campo quantistico per la sua invarianza rispetto a trasformazioni simplettiche arbitrarie. Inoltre, il risultato corrispondente rimane valido anche nel caso simmetrico, con la sostituzione delle relazioni di Weyl con quelle di Clifford (C (z) C (z′) + C (z′) C (z) = 0, C (z) C (z′)* + C (z′)* C (z) = 〈z, z′〉, qualunque siano z e z′ in L). Ciò dà luogo a una classe generale di automorfismi non implementabili nel contesto delle W*-algebre, un contesto in cui si richiede che T soddisfi una condizione del tipo Hilbert-Schmidt.

Mentre il formalismo delle C*-algebre elimina alcune divergenze di base della teoria quantistica dei campi, tra cui quella connessa con funzioni quadratiche, per occuparsi delle divergenze connesse a termini non lineari oltre a quelli quadratici si è costretti a tornare nel contesto delle W*-algebre.

5. Le W*-algebre e la loro teoria L₂

La motivazione di base che spinse von Neumann ad affrontare il problema di una teoria generale delle W*-algebre sembra essere stata la loro intima connessione con i fondamenti matematici della meccanica quantistica. Il fatto di non conoscere la loro struttura costituì, apparentemente, un blocco al progresso nel contesto non commutativo, che era chiaramente l'aspetto essenziale della teoria quantistica. Allo stesso tempo, peraltro, motivazioni secondarie ma significative vennero dalle implicazioni della teoria delle rappresentazioni dei gruppi e dalla ricerca di una generalizzazione infinito-dimensionale dei teoremi di struttura di Wedderburn.

Von Neumann collaborò con i fisici Paul Jordan e Eugene Wigner sulle questioni del formalismo algebrico, con Oswald Veblen su quelle di tipo geometrico e con Francis Murray relativamente alle W*-algebre. Von Neumann e Murray chiamarono le W*-algebre ‛anelli' o ‛anelli di operatori', ed esse sono note anche col nome di ‛algebre di von Neumann'. La linea di ricerca sulle W*-algebre, analogamente alla teoria delle C*-algebre, si sviluppò in parte al di fuori della lunga tradizione dell'algebrizzazione dell'analisi funzionale rappresentata da Riesz, Banach, Stone e, indirettamente, da Norbert Wiener e da molti altri, tra cui numerosi rappresentanti della scuola polacca. Fu però la sfida posta dagli importanti problemi irrisolti nella teoria quantistica, che sembra essere la versione della geometria non commutativa nel mondo fisico, a dare una priorità e un interesse speciale alle linee di sviluppo sia delle W*- che delle C*-algebre.

Questi problemi, già abbastanza seri alla fine degli anni venti, avevano portato Heisenberg e Pauli a sviluppare una teoria formale, di vasta portata e invariante, dell'elettrodinamica quantistica, che tuttavia forniva risposte senza senso fisico (infinite) - le cosiddette ‛divergenze dell'ultravioletto' - ad alcune delle questioni più semplici. Contemporaneamente, peraltro, si stavano facendo progressi matematici importanti, il più notevole dei quali fu il teorema di unicità di Stone-von Neumann per gli operatori di Schrödinger. In ogni caso questo lavoro non contribuì molto a risolvere i problemi della teoria quantistica non lineare di campo.

Negli anni trenta Stone continuò a rifinire la teoria spettrale commutativa, che aveva attratto l'attenzione di altri, tra i quali Shizuo Kakutani, e che pochi anni più tardi sarebbe stata definita più precisamente grazie al lavoro della scuola russa. Il teorema di approssimazione di Stone-Weierstrass, che si applica a spazi compatti (o localmente compatti) arbitrari, rappresentò un importante contributo in questo contesto. Von Neumann, comunque, aveva coraggiosamente intrapreso un programma per trattare direttamente l'aspetto specificamente non commutativo. Il teorema del ‛doppio-commutante' rappresentò una straordinaria dimostrazione e una decisa conferma dell'efficacia dello spazio di Hilbert nel compensare la infinito-dimensionalità evidentemente richiesta dalla meccanica quantistica. La relazione di commutazione di Heisenberg pq, - qp= - ih/2π ‛funzionava' empiricamente ma, evidentemente, implicava il fatto che le quantità p e q (interpretate come posizione e quantità di moto) non potevano essere rappresentate da matrici finito-dimensionali.

In un contesto infinito-dimensionale è logico presupporre che per un teorema di struttura sia necessaria la presenza di una chiusura topologica e, nello spazio di Hilbert, la topologia appropriata è la topologia dell'operatore, sia debole che forte. Per un insieme lineare di operatori, la chiusura in ciascuna di queste topologie è equivalente alla chiusura nell'altra. La topologia debole sugli operatori S è definibile come la più debole topologia in cui 〈Sx,y〉 è una funzione continua di S per vettori arbitrari x e y nel soggiacente spazio di Hilbert H. Von Neumann aveva iniziato la sua trattazione generale degli ‛anelli' prendendo in considerazione quelli debolmente chiusi e inoltre autoaggiunti, contenenti cioè insieme a ogni operatore S anche il suo aggiunto S*. L'esempio commutativo più semplice è l'anello L_∞ (M) di tutte le moltiplicazioni per funzioni misurabili limitate che agiscono sullo spazio di Hilbert L₂ (M) di tutte le funzioni misurabili su un dato spazio di misura M. In realtà, questo risulta essere essenzialmente il solo esempio commutativo, se si prescinde dalla ‛molteplicità'.

Se A è una W*-algebra, allora l'insieme di tutti gli operatori (limitati) che commutano con ogni elemento di A è ancora una W*-algebra, indicata con A′, e secondo il teorema del doppio-commutante, il suo commutante, corrispondentemente indicato con A″, è identico ad A. Tale teorema, che una volta formulato esplicitamente non è difficile da dimostrare, segna l'inizio dell'analisi non commutativa moderna e ha dato origine a una serie di classici articoli relativi agli ‛anelli di operatori' che, come si è detto, possono forse essere considerati il più importante lavoro originale nella matematica del XX secolo. Questi lavori hanno immediatamente determinato risultati essenziali nella teoria dello spazio di Hilbert, rendendo al contempo possibile il programma di von Neumann e Murray relativo alla riduzione della teoria globale delle W*-algebre nella teoria ‛locale' dei ‛fattori', unitamente a un'appropriata teoria d'integrazione per legare insieme i fattori.

Murray e von Neumann capirono che gli elementi per la costruzione delle W*-algebre erano questi ‛fattori', definiti come anelli A, i cui centri (l'intersezione di A con A′) erano banali. Inizialmente non era affatto ovvio che oltre ai fattori conosciuti, cioè tutti gli operatori limitati su uno spazio di Hilbert, ne esistessero altri. Von Neumann sviluppò delle costruzioni per i fattori ‛approssimatamente finiti', i quali risultarono tutti equivalenti tra loro, anzi essenzialmente equivalenti all'algebra di Clifford su uno spazio di Hilbert. Quest'algebra è notevole per la sua semplicità e universalità. Essa esemplifica la ‛geometria continua', una delle più memorabili esemplificazioni di una varietà della geometria non commutativa dovuta a von Neumann. La funzione dimensione su questa geometria prende dei valori continui da 0 a 1, in corrispondenza con i valori della traccia (opportunamente normalizzata) nell'algebra infinita di Clifford.

Questo fattore interessante è sostanzialmente l'unico nuovo che realmente ‛viene fuori' in modo essenziale nelle applicazioni analitiche al di fuori della stessa teoria della W*-algebra. Murray e von Neumann non potevano sapere che gli altri fattori, riguardo ai quali abbiamo ora notevoli conoscenze, sono troppo complicati e disparati per servire come base per un esplicito teorema di struttura paragonabile a quello di Wedderburn; tuttavia, ciò che risulta convincente nella teoria della molteplicità globale per le W*-algebre, in contrasto con la loro struttura locale (fattoriale), è il fatto che essa procede lungo linee naturali ed esplicite.

Gli anelli e i fattori sono gli analoghi non commutativi delle algebre L_∞, ma spesso, ad esempio nel caso commutativo, è più vantaggioso utilizzare spazi di tipo L₂, malgrado che i vettori in questo spazio non abbiano bisogno di essere limitati. Il concetto di ‛algebra di Hilbert' fornisce l'analogo della teoria commutativa L₂ ed è alla base del teorema di Plancherel per gruppi unimodulari localmente compatti, così come delle strutture dei campi quantistici, della teoria della probabilità non commutativa e di altre applicazioni.

Un'algebra di Hilbert è il completamento di un'algebra ‛pre-hilbertiana' A, che può essere definita come un'algebra associativa complessa con un'identità che ammette un'operazione aggiunta * assieme a un prodotto interno 〈a,b〉 tra ciascuna coppia di elementi a e b di A che soddisfi le condizioni: 1) 〈ab,c〉 = 〈b,a*c〉, e 〈a*,b*〉 = 〈b,a〉; 2) per ogni a data e tutte le x in A, ∥ax∥ ≤ K ∥x∥ per un'opportuna costante K= K(a); si è assunto qui, per semplicità espositiva, che A abbia un'identità, ma ciò non è essenziale. Un semplice esempio può essere quello dell'algebra di tutte le funzioni continue su una varietà compatta, con * interpretata come la coniugazione complessa, e 〈a,b〉 come il prodotto interno in L₂, ∫ ab*, di a e b. L'esempio non commutativo più semplice è l'algebra di tutte le matrici n × n con a* interpretato come l'aggiunto hermitiano e 〈a,b〉 = tr(ab*). Quest'algebra è isomorfa all'algebra di Clifford su l'n-spazio, generato dagli elementi di una base e₁, ..., e_n assieme alle relazioni e_j e_k + e_k e_j = 2δ_jk. L'algebra di Clifford su uno spazio di Hilbert è definita allo stesso modo, a parte la rinormalizzazione della traccia, così che l'identità possiede la traccia unitaria in tutte le dimensioni.

Il completamento di Hilbert di un'algebra pre-hilbertiana A definisce un'algebra di Hilbert completa H, che è la stessa per tutti i sottospazi densi pre-hilbertiani. In generale gli elementi di H non soddisferanno la condizione 2), una situazione compensata però dall'‛algebra limitata' B di un'algebra di Hilbert, che consiste in tutti i vettori x in H tali che l'applicazione a → ax, definita dalla chiusura della moltiplicazione per a a sinistra, sia limitata. Le W*-algebre L e R generate dalle moltiplicazioni a sinistra e a destra per elementi di B sono commutanti l'una dell'altra. Ciò serve in particolare a costituire la versione L_∞ dell'algebra di Clifford, come anche di L o R, che sono interscambiate dall'azione indotta di * su H.

In aggiunta ad altre applicazioni importanti, quali ad esempio l'analisi armonica sui gruppi di Lie, le algebre di Hilbert forniscono una formulazione universale, probabilmente la più semplice, per campi quantistici liberi. Ciò è indipendente dalla statistica (cioè dal fatto che si tratti di bosoni, fermioni o di un prodotto diretto come nell'elettrodinamica quantistica) e porta, in ultima analisi, a un metodo per trattare espressioni essenzialmente non lineari nei campi quantistici quali le lagrangiane d'interazione.

La teoria è associata con la ‛teoria dell'integrazione non commutativa', che include la teoria astratta di Lebesgue ed è molto più potente della teoria della generale integrazione della C*-algebra, come conseguenza dell'invarianza unitaria dell'integrale nella teoria della W*-algebra.

6. I campi quantistici universali liberi

In aggiunta ad altre importanti applicazioni, le algebre di Hilbert forniscono la più semplice trattazione generale invariante per la teoria del campo quantistico libero. Questa teoria è essenzialmente la stessa per tutti i gruppi di simmetria e tutte le statistiche (bosoni, fermioni o entrambi). Le rappresentazioni più familiari, per i campi liberi, sono la rappresentazione di particella libera e quella dell'oscillatore armonico per i campi di bosoni, che diagonalizzano rispettivamente i numeri di particelle e il campo quantistico a un istante fissato. La rappresentazione di ‛onda complessa', meno familiare ma matematicamente più potente, può essere considerata formalmente come una ‛diagonalizzazione' del campo quantistico complesso piuttosto che di quello reale, cioè lo rappresenta come un operatore di moltiplicazione (benché non normale nello spazio di Hilbert). Opportunamente sviluppata, la rappresentazione di onda complessa è formalmente la stessa per campi fermionici ed è chiaramente invariante; inoltre, essa è la rappresentazione più semplice da un punto di vista simbolico.

La quantizzazione di campo libero universale prende inizio da uno spazio di ‛particella singola', o ‛campo classico', formulato come uno spazio di Hilbert complesso H. Per esempio, H può essere lo spazio di Hilbert di tutte le soluzioni delle equazioni di Maxwell che hanno una norma finita Lorentz-invariante. Questi spazi definiscono rappresentazioni unitarie dei gruppi di simmetria associati in cui il generatore dell'evoluzione temporale rappresenta l'energia di ‛particella singola' e le altre quantità fisiche sono rappresentate da altri generatori o da loro combinazioni.

Le diverse rappresentazioni del campo quantistico libero F(H) su H contengono, in una forma o nell'altra, quattro entità di base: 1) lo ‛spazio di Hilbert del campo quantizzato' K, che è, nella rappresentazione di particella (Fock-Cook), una somma diretta di potenze tensoriali di H con se stesso; 2) un'applicazione lineare C da H in operatori ‛creazione' in K, che soddisfa le semplici relazioni di commutazione o di anticommutazione; 3) una rappresentazione unitaria continua Γ del gruppo unitario U(H) su H nel gruppo U(K) di tutti gli operatori unitari su K, che canonicamente associa le trasformazioni su H a trasformazioni su K, conserva la positività dell'energia e commuta con C(z): Γ(U)C(z) Γ(U)*= C(Uz); 4) uno stato di ‛vuoto' v che è invariante per tutte le Γ(U) le cui trasformate rispetto a C(z) generano K.

Nella rappresentazione di onda complessa, la positività dell'energia è implementata dalla rappresentazione di K per mezzo di quelle che sono sostanzialmente funzioni intere, analitiche e complesse su H nei campi di bosoni, e per mezzo di spinori analoghi (infinito-dimensionali) nei campi di fermioni. La sistemazione formale può essere fatta in termini puramente algebrici, che richiedono solamente la completezza e la chiusura per ottenere il campo quantizzato nella forma descritta sopra.

Più specificamente, sia H* lo spazio di tutti i funzionali lineari z* su H della forma z*:u → 〈u,z〉 per qualche vettore z in H. Inoltre, sia L la somma diretta di H e H* e denotiamo con P la *-algebra associativa e commutativa libera generata da L assieme a una identità, dove * denota l'operazione aggiunta che interscambia z con z*. Gli elementi di P sono chiamati ‛polinomiali' su L; gli elementi della sottoalgebra P⁺ generata da H (e rispettivamente della sottoalgebra P^- generata da H*) assieme con 1 sono chiamati polinomiali (non funzioni polinomiali) olomorfi (rispettivamente anti-olomorfi).

Una funzione a valori complessi f su H (assunto di dimensione maggiore di uno) è intera (o anti-intera) se la sua restrizione a ogni sottospazio finito-dimensionale F è una funzione intera (o anti-intera) su F. L'algebra P⁺ è *-algebricamente isomorfa all'algebra delle funzioni polinomiali anti-olomorfe attraverso l'unico isomorfismo che porta il vettore z in H nella funzione f_z* (u) = 〈u,z〉.

L'integrazione funzionale, che generalizza la teoria di Wiener del moto browniano, è formulata in termini di un funzionale lineare positivo e su P che è invariante rispetto a Γ(U) e che soddisfa le seguenti equazioni: 1) e(zw*)= 〈z,w〉 per z, w in H arbitrari; 2) e(pq)=e(p)e(q), se p e q sono polinomiali basati su sottovarietà ortogonali di H, dove un elemento di P appartiene a un sottospazio M di H se è contenuto nell'algebra generata dalle z e dalle z* con z in M. In conseguenza dell'equazione 2), e può essere dato esplicitamente per mezzo delle restrizioni ai sottospazi monodimensionali di H. Quindi nel campo di bosoni, e(zⁿz*^m) = n!δ_nm ∥z∥²ⁿ; per z arbitrari in H. C(z) è definibile come la chiusura dell'operatore su P⁺, p(z) → zp(z) - e pertanto soddisfa le usuali relazioni di commutazione canoniche - e Γ(U) come la chiusura dell'operatore in K che porta p(z) in p(Uz).

Per costruire il campo di fermioni, si inizia con la *-algebra C′, associativa libera ma non commutativa, generata da L e si forma il quoziente C di quest'algebra per lo*-ideale generato dagli elementi di C′ della forma wz*+z*w - 2 〈w,z〉 per w,z in arbitrari H. La sottoalgebra di C generata dalle z in H è ora C⁺ e i suoi elementi sono ‛olomorfi', mentre quelli generati dalle z* (per z in H) sono ‛anti-olomorfi'. Il funzionale di aspettazione e ha le stesse proprietà generali che aveva in precedenza, ma le sue restrizioni monodimensionali ora prendono la forma e(z) = e(z*) = 0, e(zz*) = ∥z∥². L'operatore speciale ma invariante Γ (- 1) = Ω interviene nella definizione della pseudo-derivazione come un'applicazione lineare d di C su se stessa con le proprietà che d(uv)=(du)v+(Ωu)dv per u e v in C arbitrari; inoltre, per ciascun elemento z in H esiste un'unica pseudo-derivazione D₀ (z) su C che trasporta w in 〈w,z〉 e w* in 0. D₀ (z) è l'aggiunto di C₀ (z), l'operazione di moltiplicazione a sinistra per z su C⁺, e C(z) è appropriatamente definibile come l'aggiunto di D₀ (z) che eguaglia la chiusura di C₀ (z) (e soddisfa le usuali relazioni di anticommutazione).

Non è difficile verificare la validità delle quattro condizioni date sopra e queste caratterizzano in maniera univoca i campi liberi unitariamente equivalenti. Da un punto di vista tradizionale o elementare, le rappresentazioni di particella e oscillatore armonico del campo libero possono apparire più semplici, ma l'olomorfismo nella rappresentazione di onda complessa permette rappresentazioni molto più efficaci degli operatori su K attraverso le quali si riesce a costruire una versione infinito-dimensionale del lemma di Poincaré il quale, a sua volta, fornisce una controparte rigorosa ad alcune delle espressioni della teoria multidimensionale dei campi interagenti, altrimenti puramente simboliche.

7. Un esempio: le funzioni non lineari dell'equazione d'onda quantistica

Il campo relativistico più semplice è quello dato dall'equazione d'onda reale, che fornisce una rappresentazione (complessa!) unitaria e irriducibile del gruppo conforme e del suo sottogruppo di Poincaré. È opportuno chiarire ed esemplificare la quantizzazione astratta appena descritta attraverso casi concreti come il seguente.

Consideriamo uno spazio-tempo minkowskiano M₀ di dimensione pari, maggiore o uguale a quattro per evitare degenerazioni banali. Le soluzioni normalizzabili dell'equazione d'onda (∂0² - Δ) f=0, dove ∂₀ = ∂/∂x₀ (x₀ indica il tempo e Δ il laplaciano sullo spazio) sono distribuzioni che soddisfano questa equazione, la cui norma ∥CF(x₀)∥² + ∥C^-1∂₀ F(x₀)∥², in cui F (x₀) indica la funzione sullo spazio f (x₀, x), dove x è un punto variabile dello spazio e C = (- Δ)^1/4, è finita. Sul duale di M, cioè nel cosiddetto spazio dei ‛momenti', la norma ha un'apparenza locale in termini della trasformata di Fourier di f, ma nello spazio fisico ha la forma non locale data qui; ciò non ha peraltro alcuna conseguenza. Uno spazio complesso è ottenuto introducendo, come struttura complessa, la trasformata di Hilbert rispetto al tempo. Questa è una isometria della metrica data e dà origine a una rappresentazione unitaria del gruppo conforme in cui il generatore autoaggiunto dell'evoluzione temporale è positivo.

L'equazione d'onda quantizzata prende la stessa forma, eccetto che il campo f(x) è ora una distribuzione i cui valori sono operatori hermitiani su K. In altri termini, se k(x) è una funzione regolare e reale, di prova, di supporto compatto su M₀, l'integrale (nel senso usuale associato con le distribuzioni) ∫ f (x) k (x) d₄ x è un operatore hermitiano in K. I ‛valori' di f (x) in punti differenti di M in generale non commutano, ma soddisfano le relazioni di commutazione della forma [f (x), f (y)] = iD (x - y), dove D è una distribuzione reale su M₀, una soluzione singolare dell'equazione d'onda la cui forma esplicita non è qui necessaria. Questa stessa relazione di commutazione è perfettamente regolare; in termini di funzioni di prova h e k si ha:

[F(h),F(k)] = i∫ ∫D(x - y)h(x)k(y)dxdy.

Per un campo libero, l'energia è data semplicemente come generatore autoaggiunto del gruppo unitario a un parametro Γ(U(t)), dove U(t) è la trasformazione unitaria su H che fa progredire di un tempo t ogni soluzione f dell'equazione d'onda. Lo stesso avviene per le altre grandezze quantistiche di base. Le divergenze della teoria non lineare del campo quantistico si verificano non tanto nella teoria di puro campo libero, quanto piuttosto nelle espressioni simboliche, locali e non lineari che sono coinvolte nella lagrangiana o nell'hamiltoniana di interazione dei campi interagenti, sia per auto-interazioni sia per interazioni tra campi differenti.

Il problema è che le più semplici funzioni simboliche non lineari del campo quantistico, ad esempio il suo quadrato o potenze più alte, non solo non hanno a priori alcun significato, ma i tentativi di definizione attraverso argomenti di limite confermano fortemente l'assenza di significato matematico. Ad esempio, l'integrale del quadrato regolarizzato dell'approssimazione al campo, relativa a una funzione di prova regolare, chiaramente diverge a più infinito nel limite della rimozione della regolarizzazione. Non c'è dubbio, pertanto, che in assenza di qualche struttura addizionale, come quella fornita dall'interpretazione del prodotto di Wick per espressioni non lineari, la teoria sia irrimediabilmente divergente.

Questo fatto non implica in alcun modo che tale interpretazione abbia necessariamente un senso fisico, ma la sua semplicità matematica, espressa nei termini delle forme differenziali quantistiche, assieme alle diverse verifiche empiriche dei risultati di questa interpretazione, lascia pochi dubbi al riguardo. Essenzialmente, questa interpretazione dice che una ipotizzata lagrangiana di interazione relativisticamente invariante, quale L = ∫_M f (x)^p d₄ x, è data a priori solamente come una forma quantistica; è allora compito dei teorici rappresentare questa forma come un tipo di operatore differenziale densamente definito nello spazio di Hilbert, proprio come in fisica classica è spesso necessario risolvere una data equazione differenziale che inizialmente determina la teoria.

Per formulare la data espressione simbolica come una forma quantistica consideriamo, nel caso p=4, i suoi commutatori successivi con quattro valori regolari di f(x) e poniamo F(k_j) = ∫ f (x) k_j (x) d₄ x, dove j=1, 2, 3, 4. Il risultato è formalmente:

Il lato destro di questa equazione è perfettamente definito e soddisfa le condizioni formali per definire una forma quantistica di grado 4. La dimostrazione dell'esistenza di un operatore hermitiano corrispondente in K richiede un'estensione appropriata della teoria delle forme quantistiche finito-dimensionali al caso infinito-dimensionale, ottenibile grazie all'analisi nella rappresentazione di onda complessa.

8. Il lemma di Poincaré infinito-dimensionale e la teoria quantistica dei campi multidimensionali

Il lemma di Poincaré può essere formulato parallelamente per i campi di bosoni, di fermioni o dei loro prodotti tensoriali, ma per semplicità qui ci limiteremo al caso dei bosoni. Assumeremo che l'operatore E di energia di particella singola abbia la proprietà che exp [-sE] è un operatore di Hilbert-Schmidt per s>0 (v. operatori, teoria degli, vol. XI). A tal fine è necessario che vi sia equivalenza conforme della varietà H₀, soluzione dell'equazione d'onda in M₀, e la varietà soluzione dell'equazione d'onda conforme nel ricoprimento universale M della compattificazione conforme di M₀. M è conformemente equivalente a R¹ × S³, conosciuto anche con il nome di ‛universo di Einstein', in cui R¹ rappresenta un asse del tempo che non è completamente equivalente a quello in M₀, benché localmente la differenza sia del secondo ordine. D'altra parte, l'operatore energia E in M domina (per esempio, è più grande di) quello in M₀ e inoltre ha la proprietà di Hilbert-Schmidt citata in precedenza. L'equazione d'onda del campo quantizzato è la stessa, entro l'equivalenza unitaria, sia che l'equazione d'onda sia formulata come al solito su M₀ o in maniera conforme su M.

Sia D lo spazio dei vettori interi per E e D* lo spazio dei vettori interi per l'energia di campo quantizzato, cioè il generatore autoaggiunto del gruppo a un parametro Γ (exp (tE)), entrambi presi nelle loro topologie naturali associate con vettori interi (i vettori analitici andrebbero egualmente bene nella loro topologia naturale). Un n-cociclo può essere in questo caso definito come un'applicazione continua e multilineare da Dⁿ sullo spazio di tutte le forme continue lineari alternate su D* che soddisfano le seguenti condizioni: 1) F(z₁, ..., z_n) è una funzione simmetrica dei vettori z₁, ..., z_n; 2) per arbitrari z₁, ..., z_n e z′ in D, [F(z₁, ..., z_n), f(z′)] = [F(z′, ..., z_n), f(z₁)]. Il lemma di Poincaré allora asserisce che ogni n-cociclo è esatto, cioè esiste un operatore lineare continuo F su D* tale che

F(z₁, ..., z_n) = ∂(z₁), ..., ∂(z_n)F,

dove ∂(z) indica l'operatore F → [F, f(z)]. Inoltre, F è unico a meno di una costante additiva ed esiste un'applicazione continua (‛quantizzazione') fra gli n-cocicli e le forme nella topologia dei vettori interi. Applicato al caso dell'equazione d'onda, ciò implica l'esistenza di ∫_M f(x)^p dx come operatore hermitiano densamente definito e non nullo su D*, avente un'estensione autoaggiunta, per ogni valore pari di p ≥ 4. Nel caso conformemente invariante p=4, l'operatore è già essenzialmente autoaggiunto.

Non c'è nulla di molto speciale riguardo all'equazione d'onda in questo contesto, a parte la sua invarianza conforme. Equazioni d'onda massive, comunque, richiedono ulteriori considerazioni, principalmente per il fatto che la larghezza (o dispersione) non banale della massa deve essere incorporata nella struttura di particella singola. Questo fatto è osservabile empiricamente in tutti i casi eccetto quelli dei due fermioni apparentemente stabili (elettroni e protoni), le cui dispersioni di massa possono semplicemente essere troppo piccole per essere rivelate.

9. Conclusione

La geometria non commutativa si sta sviluppando in molte direzioni, anche se non in tutte essa si è già profondamente radicata, e in questo articolo abbiamo potuto presentare soltanto alcuni dei suoi aspetti più significativi. Essa si sta estendendo in direzione dell'algebra e della topologia, cercando di giungere a generalizzazioni non commutative della teoria commutativa usuale. La coomologia ciclica di Connes utilizza proficuamente un operatore introdotto vent'anni prima da G. Rinehart, fornendo un nuovo indirizzo di studio relativamente alla teoria algebrica della coomologia. Il lavoro molto incisivo di Kasparov nella K-teoria è riuscito a far luce su molti problemi classici, come le congetture di Novikov. Studi molto interessanti di A. Kirillov e Bertram Kostant, relativi alla quantizzazione simplettica, o kählerizzazione, per le equazioni d'onda non lineari e al metodo delle orbite nella teoria delle rappresentazioni dei gruppi, rappresentano altri stimolanti campi di applicazione della geometria non commutativa.

La teoria della distribuzione di Clifford fornisce un interessante parallelo con quella della distribuzione normale, e il suo sviluppo ulteriore dovrebbe non solo rappresentare un esempio cruciale per la teoria non commutativa della probabilità, ma dovrebbe risultare di grande importanza anche per i campi di fermioni. La coomologia del gruppo di Heisenberg discussa in precedenza è essenzialmente infinitesimale e ha bisogno di ulteriore considerazione nel contesto globale.

Il campo che forse più di ogni altro deve essere ulteriormente sviluppato all'interno del contesto della geometria non commutativa è la teoria quantistica dei campi, in modo da riuscire a chiarire, ad esempio, la connessione tra la sua formulazione in M₀ e in M, che essenzialmente si deforma in M₀ nel limite di curvatura nulla nella sua componente S³. Ad ogni modo, indipendentemente dalla situazione in M₀, è ora divenuto possibile trattare rigorosamente gli spettri e le asintoticità delle teorie convergenti in M, che è lo spazio-tempo quadridimensionale massimale simmetrico.

Ci auguriamo che questa introduzione alla geometria non commutativa incoraggi queste e molte altre ricerche correlate.

BIBLIOGRAFIA

Baez, J. C., Segal, I. E., Zhou, Z., Introduction to algebraic and constructive quantum field theory, Princeton, N. J., 1992.

Connes, A., Noncommutative geometry, San Diego, Cal., 1994.

Dixmier, J., Les algèbres d'opérateurs dans l'espace hilbertien, Paris 1969.

Gel′fand, I. M., Collected papers, 3 voll., Berlin 1987-1989.

Jerison, D., Singer, I. M., Stroock, D. M. (a cura di), The legacy of Norbert Wiener: a centennial symposium, Providence, R. I., 1997.

Neumann, J. von, Mathematical foundations of quantum mechanics, Princeton, N. J., 1955.

Neumann, J. von, Collected works, 6 voll., New York 1961-1963.

Sakai, S., C*-algebras and W*-algebras, Berlin 1971.

Segal, I. E., Mathematical problems of relativistic physics, Providence, R. I., 1963.