GIOCHI_MATEMATICI
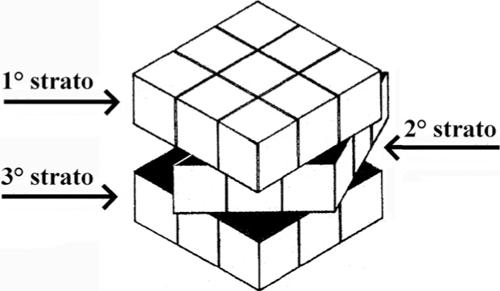
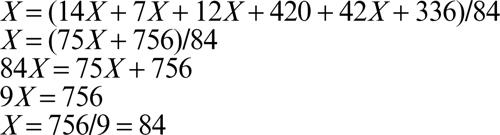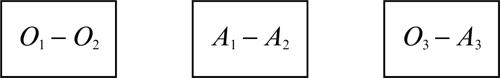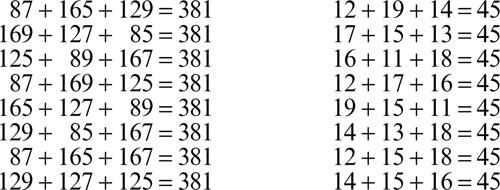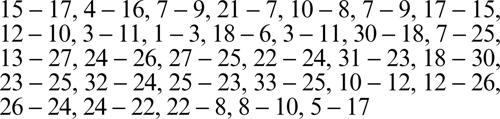GIOCHI_MATEMATICI
GIOCHI MATEMATICI
Con il termine matematica ricreativa si intende quel vasto insieme di questioni logico-matematiche che vengono affrontate per spirito ludico e puro piacere personale e non per la necessità di approfondire degli argomenti di studio o di risolvere casi concreti. Il materiale di cui questa disciplina si occupa si presenta sotto varie forme (enigmi, problemi, paradossi, puzzle, rompicapi, giochi di strategia, costruzioni, trucchi illusionistici ecc.) e coinvolge diverse branche matematiche (aritmetica, algebra, analisi, geometria, logica, topologia, calcolo combinatorio, calcolo delle probabilità ecc.).
La matematica ricreativa ha origini antichissime: già nel papiro egiziano di Rhind, risalente al 1650 a.C., è documentato l’enigma delle sette case, mentre nel Shu-Ching, un testo cinese del vii secolo a.C., sono descritti i quadrati magici.
I problemi e gli enigmi qui illustrati costituiscono una limitata selezione dei più interessanti giochi di matematica ricreativa prodotti dall’antichità a oggi. Sono suddivisi in due principali categorie (giochi matematici e giochi logici) in base a una ripartizione qui di seguito esposta.
■ Giochi matematici
1. Enigmi sequenziali: problemi che si risolvono effettuando una determinata sequenza di calcoli o impostando opportune equazioni algebriche.
2. Enigmi laterali: problemi che, apparentemente, richiedono un intervento matematico piuttosto elaborato, ma che in realtà possono essere risolti abbastanza facilmente, grazie a una trovata ingegnosa.
3. Enigmi ingannevoli: problemi risolubili in maniera relativamente semplice, ma il cui enunciato induce il solutore a fornire una risposta errata, o gli impedisce addirittura di trovarla.
4. Paradossi matematici: problemi che non contengono inganni nell’enunciato, ma la cui soluzione porta a un risultato alquanto diverso da quello che ci si poteva intuitivamente aspettare.
■ Giochi logici
5. Percorsi logici: problemi risolvibili attraverso una sequenza di ragionamenti puramente logici, senza dover eseguire complessi calcoli matematici.
6. Incasellamenti logici: questioni riguardanti la sistemazione di un insieme di elementi, all’interno di una matrice quadrata, nel rispetto di determinate condizioni iniziali.
7. Rompicapi bidimensionali: giochi di ragionamento che possono essere eseguiti solo manipolando degli appositi elementi solidi, disposti in uno spazio a due dimensioni.
8. Rompicapi tridimensionali: giochi di ragionamento che possono essere eseguiti solo manipolando degli appositi elementi solidi, disposti in uno spazio a tre dimensioni.
La fonte principale dei riferimenti temporali adottati, qui e nel seguito, è la Chronology of recreational mathematics, stilata dal divulgatore statunitense David Singmaster, nel 1998.
1. Enigmi sequenziali
Problemi che si risolvono effettuando una determinata sequenza di calcoli o impostando delle opportune equazioni algebriche.
1.1 Le sette case (Papiro di Rhind, 1650 ca a.C.)
Il papiro di Rhind è il più corposo papiro egizio di contenuto matematico di cui si ha conoscenza. Scritto in ieratico, largo 33 centimetri e lungo 3 metri, fu scoperto dall’antiquario scozzese Henry Rhind, che lo acquistò nel 1858 in un mercatino di Luxor, in Egitto. Attualmente è conservato al British Museum. Contiene diverse tabelle di frazioni e 84 problemi di varia natura (aritmetici, algebrici e geometrici), con le relative soluzioni dettagliate. Tra gli enigmi in esso proposti, vi è l’enigma delle sette case.
In una proprietà ci sono 7 case.
In ogni casa ci sono 7 gatti.
Ogni gatto acchiappa 7 topi.
Ogni topo mangia 7 spighe.
Ogni spiga dà 7 heqat (l’heqat è una misura di capacità pari a circa 4,785 litri) di grano.
Quante cose ci sono in tutto in questa storia?
■ Soluzione. Se si esclude dal conteggio delle “cose” la proprietà citata all’inizio, si ha:
• case: 7
• gatti: 7 × 7 = 72 = 49
• topi: 7 × 7 × 7 = 73 = 343
• spighe: 7 × 7 × 7 × 7 = 74 = 2401
• heqat: 7 × 7 × 7 × 7 × 7 = 75 = 16.807
• totale: 7 + 49 + 343 + 2401 + 16.807 = 19.607
In pratica, per risolvere il problema, bisogna effettuare la somma degli elementi di una progressione geometrica di ragione 7. Al giorno d’oggi, un calcolo del genere può essere svolto agevolmente ricorrendo a una calcolatrice, ma richiedeva un notevole impegno al tempo degli egizi.
■ Nota. Nel corso dei secoli, sono state elaborate diverse versioni di questo problema, alcune anche ingannevoli, come la seguente:
Mentre andavo a Saint Ives
Incontrai un uomo con sette mogli.
Ogni moglie aveva sette sacchi,
Ogni sacco aveva sette gatti,
Ogni gatto aveva sette mici;
Mici, gatti, sacchi e mogli,
In quanti andavano a Saint Ives?
In questo caso, la risposta (beffarda) è: una sola persona. Infatti, solo il narratore andava a Saint Ives. Tutti gli altri, andavano nella direzione opposta.
1.2 La cisterna (Chiu Chang Suan Shu, 150 a.C.)
L’enigma della cisterna è contenuto nel Chiu Chang Suan Shu (Nove capitoli sulle arti matematiche), il più famoso testo cinese di matematica. Affronta questioni concrete di ingegneria e di contabilità, oltre a illustrare pratiche tecniche di calcolo. Rivolto a lettori non principianti, contiene ben 246 problemi con le indicazioni generali per poterli risolvere. Per riempire una cisterna ci sono tre rubinetti. Il primo impiega 10 ore per riempirla, il secondo impiega 20 ore e il terzo 60 ore.
Se si aprono tutti e tre i rubinetti, quanto tempo ci metterà la cisterna a riempirsi?
■ Soluzione. In assoluto, se un rubinetto impiega X ore per riempire tutta la cisterna, in una sola ora riempie 1/X di cisterna. Di conseguenza, in un’ora:
• il primo rubinetto riempie 1/10 di cisterna;
• il secondo rubinetto riempie 1/20 di cisterna;
• il terzo rubinetto riempie 1/60 di cisterna.
Per cui, in un’ora, i tre rubinetti insieme riempiono:
In definitiva, la cisterna verrà riempita in 6 ore.
1.3 L’epitaffio (Diofanto, 250 ca)
Il matematico greco Diofanto volle che sulla propria tomba fosse inciso il seguente epitaffio, in modo che chiunque fosse in grado di sapere quanti anni visse.
«Dio gli concesse di rimanere fanciullo per un sesto della sua vita, e trascorso un altro dodicesimo, Egli gli coperse le guance di peluria; dopo un settimo della sua vita Egli gli accese la fiaccola del matrimonio, e cinque anni dopo il matrimonio gli concesse un figlio. Purtroppo questo bambino nato dopo tanto tempo fu sfortunato: dopo aver raggiunto la metà della vita di suo padre, fu portato via da un Destino crudele. Dopo aver consolato il proprio dolore con la scienza dei numeri per quattro anni, pose termine alla propria vita».
Quanti anni visse Diofanto?
■ Soluzione. Se si indica con X il numero di anni vissuti da Diofanto, si può impostare la seguente equazione:
da questa, svolgendo opportuni passaggi, si ricava:
In definitiva, Diofanto visse 84 anni.
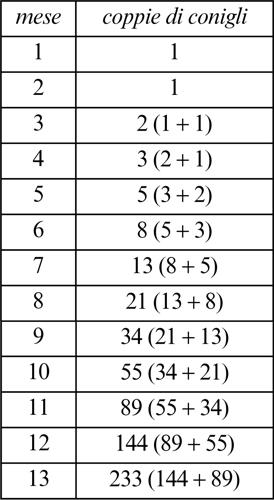
1.4 Coppie di conigli (Leonardo Fibonacci, 1202)
Il Liber abaci (1202 d.C.) è il più importante trattato medievale di matematica. Leonardo Fibonacci, figlio di un mercante pisano, lo scrisse per introdurre in Europa il sistema di numerazione decimale e gli algoritmi di calcolo da esso derivati che aveva appreso nel corso di vari viaggi compiuti in Oriente. Contiene un capitolo dedicato interamente a problemi di carattere ricreativo, chiamato scherzosamente Questioni erranti (cioè “vagabonde”, senza concrete applicazioni immediate); tra le questioni proposte vi è la seguente: supponiamo che una generica coppia di conigli coetanei cominci a procreare al compimento dei due mesi di età e che, da quel momento in poi, si riproduca regolarmente, allo scadere di ogni mese successivo. Supponiamo anche che ogni coppia di conigli generi, ogni volta, solo un’altra coppia di conigli. Se in un recinto vuoto viene posta una coppia di conigli appena nata, quante ce ne saranno in quel recinto, al termine di 12 mesi, ipotizzando che nessuna di esse muoia? (per “coppia di conigli” si intende l’insieme di un coniglio maschio e di una coniglia femmina).
■ Soluzione. Per risolvere questo problema bisogna osservare che, all’inizio di ogni mese, la quantità di nuove coppie è esattamente uguale a quella delle coppie presenti due mesi prima (trascorso un tale periodo di tempo, infatti, ciascuna di esse è in grado di procreare). Di conseguenza, la quantità di coppie presenti all’inizio di un generico mese è uguale alla quantità delle coppie presenti all’inizio del mese precedente, più quella delle coppie appena nate. Un tale valore, quindi, si può ricavare semplicemente sommando le quantità di coppie presenti all’inizio dei due mesi immediatamente precedenti, come mostrato nella tabella.
Sulla base di tali considerazioni, si deduce che, dopo 12 mesi (ovvero, all’inizio del 13° mese), nel recinto ci saranno 233 coppie di conigli.
■ Nota. Nella seconda metà del xix secolo, il matematico francese Édouard Lucas studiò a fondo le sequenze che iniziano con una qualsiasi coppia di numeri interi e nelle quali ogni valore successivo è uguale alla somma dei due che lo precedono e, memore del problema dei conigli, chiamò serie di Fibonacci quella che inizia con una coppia di 1 (ovvero: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233...). Sorprendentemente, questa particolare sequenza numerica si ritrova nei contesti più disparati, dalla biologia all’economia, dalla fisica all’informatica.
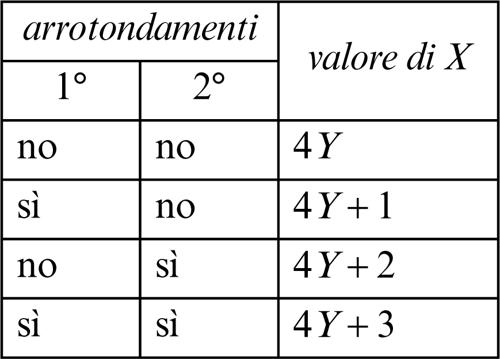
1.5 Pensa a un numero (Luca Pacioli, 1508)
Il De viribus quantitatis (1496-1508 d.C.) è un manoscritto in copia unica redatto dal matematico italiano Luca Pacioli, attualmente conservato nella biblioteca dell’università di Bologna. Composto da oltre 600 pagine, è diviso in tre parti, la prima delle quali costituisce la prima grande collezione di giochi matematici e questioni dilettevoli e riprende anche diversi problemi proposti da autori precedenti. Il gioco di magia matematica di Pacioli qui proposto è piuttosto sorprendente, in quanto le informazioni a disposizione sembrano troppo vaghe. Le sue modalità di esecuzione sono le seguenti.
1. Fornite a un vostro amico le seguenti istruzioni
a) pensa a un numero X (per esempio: 5);
b) somma al numero X la sua metà; se questa metà non è intera, arrotondala per eccesso e fammi sapere se hai dovuto effettuare un tale arrotondamento (5 + 3 = 8, arrotondando il quoziente di 5/2);
c) al risultato ottenuto, somma la sua metà; di nuovo, se questa metà non è intera, arrotondala per eccesso e fammi sapere se hai dovuto effettuare un tale arrotondamento (8 + 4 = 12, senza arrotondamenti);
d) dividi per 9 il risultato, ignorando l’eventuale resto e fammi sapere quanto ti è venuto (12/9 = 1, omettendo il resto di 3).
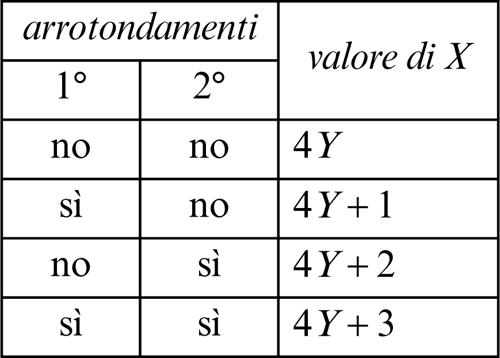
2. Conosciuto il risultato finale Y di queste operazioni, potete risalire al numero iniziale X, in funzione degli eventuali arrotondamenti effettuati dallo spettatore, consultando la seguente tabellina.
Dato che, nell’esempio indicato, il vostro amico ha dovuto arrotondare solo il quoziente della prima divisione, dovete prendere in considerazione la formula riportata nella seconda riga della precedente tabellina. Quindi, siccome il risultato comunicatovi è Y = 1, potete ricavare, correttamente:
Come mai questo procedimento funziona sempre?
■ Soluzione. Non è facile ottenere una formula generale, che consenta di risalire dal risultato finale al numero pensato all’inizio. Conviene, invece, concentrarsi sugli effetti derivanti dalle azioni previste, in funzione delle proprietà attribuibili al numero iniziale.
A tale scopo, si può osservare che, dividendo un qualsiasi numero intero X per 4, il resto ottenibile può assumere solo un valore compreso tra 0 e 3.
Di conseguenza, sotto tale aspetto, X può assumere soltanto una delle seguenti quattro forme:
(dove Y indica il quoziente intero della divisione X/4). Nella tabella sono riportati, in verticale, gli effetti prodotti dalle varie mosse previste dal gioco, in funzione della forma assunta dal numero iniziale X.
Dall’ultima riga di questa tabella emerge che, dato qualsiasi valore di X, se si divide per 9 il numero finale e si trascura il resto si ottiene sempre Y.
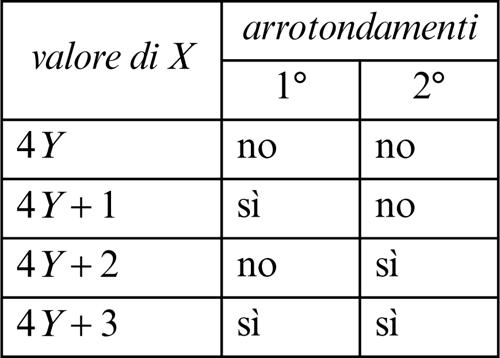
Inoltre, si può notare che ognuna delle quattro potenziali forme di X produce una diversa coppia di risposte in merito ai due possibili arrotondamenti, come evidenziato dalla seguente tabellina.
Di conseguenza, ricavato il valore di Y, è possibile risalire a quello di X, rovesciando le due colonne principali di tale tabellina e prendendo in considerazione le risposte ottenute, in merito agli eventuali arrotondamenti effettuati.
2. Enigmi laterali
Problemi che, apparentemente, richiedono un intervento matematico piuttosto elaborato, ma che in realtà possono essere risolti abbastanza facilmente, grazie a una trovata ingegnosa.
2.1 Turchi e cristiani (Niccolò Tartaglia, 1550)
L’equipaggio di un’antica galea era composto da 15 turchi e 15 cristiani. Un giorno la nave, colpita da un tremendo fortunale, stava per affondare; il capitano decise quindi, per alleggerire l’imbarcazione, di gettare in mare 15 marinai. Mentre si discuteva sui criteri da seguire per compiere questa dolorosa scelta, il membro più anziano dell’equipaggio, un turco, avanzò la seguente proposta. I 30 marinai si sarebbero disposti in circolo e poi, contando da sinistra verso destra, a partire da lui, sarebbe stato sacrificato un marinaio ogni 9, fino ad arrivare a eliminarne 15. Il criterio venne accettato all’unanimità, perché sembrava affidato totalmente alla sorte; il vecchio turco, però, dispose i marinai, in modo tale che a essere eliminati fossero solo i cristiani. Come vennero disposti i 30 marinai?
■ Soluzione. Questioni di questo tipo, non sono agevolmente affrontabili in termini rigorosamente matematici. Il sistema più pratico per risolverli è quello di riprodurre la situazione su un foglio di carta, o di simularla, utilizzando degli oggetti (come, per esempio, delle carte da gioco).
In particolare, per risolvere il problema in questione, il matematico italiano Niccolò Tartaglia, nel suo General trattato di numeri e misure, propone la seguente, ingegnosa procedura:
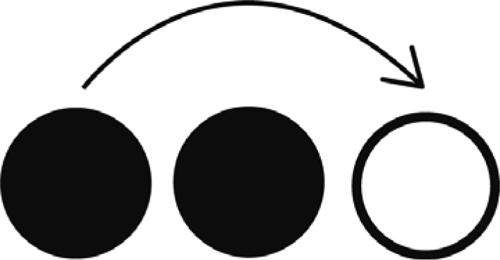
• si disegnano 30 cerchietti bianchi, per simboleggiare l’insieme globale dei marinai, e se ne sceglie uno, per indicare il marinaio più anziano, da cui iniziare il conteggio;
• successivamente, cominciando a contare di 9 in 9 (a partire da un determinato cerchietto) si anneriscono quelli, di volta in volta, toccati (escludendoli dai conteggi successivi).
• Dopo aver annerito 15 cerchietti, la situazione che si viene a generare, fornisce la disposizione iniziale cercata: i cerchietti bianchi corrispondono alle posizioni dei 15 turchi, quelli anneriti corrispondono alle posizioni dei 15 cristiani.
■ Nota. Macabri problemi di questo genere, detti di decimazione, abbondano negli antichi trattati di matematica ricreativa del medioevo (anche se, per amor di fede, in alcune versioni sono i turchi che finiscono in mare...); la loro formulazione sembra però essere ancora più antica, anche se in forma meno complessa. Diversi autori citano al riguardo un leggendario episodio di analoghe connotazioni, risalente alla rivolta antiromana della Giudea (66-70 d.C.), che avrebbe avuto come protagonista lo scrittore ebreo Giuseppe Flavio, autore del De bello Judaico.
2.2 Acqua e vino (Lewis Carroll, 1885)
Si supponga di avere due bottiglie, una contenente un litro di acqua e l’altra contenente un litro di vino. Si immagini ora di prelevare un centimetro cubo di acqua, di travasarlo nel vino e, dopo aver mescolato completamente i due liquidi, di ripassare nell’acqua un centimetro cubo della miscela così ottenuta. Al termine di tale procedura, quindi, le due bottiglie tornano a contenere un litro di liquido, ciascuna. A questo punto, la quantità di acqua presente nella bottiglia di vino è maggiore o minore della quantità di vino presente nella bottiglia di acqua?
■ Soluzione. Se si pensa di affrontare la soluzione di questo problema, cercando di interpretare matematicamente gli effetti di ogni operazione di travaso, si rischia di impelagarsi in una sequenza di calcoli, alquanto intricata e insidiosa. Si può ottenere lo stesso risultato, molto più rapidamente, considerando che le due bottiglie, alla fine, tornano a contenere un litro di liquido ciascuna. Di conseguenza, la quantità di liquido originario che manca in ognuna di esse deve necessariamente essere stata rimpiazzata con un’uguale quantità dell’altro tipo di liquido.
In definitiva, alla fine, ci deve essere tanta acqua nel vino, quanto vino c’e nell’acqua.
■ Nota. A onor del vero, bisogna precisare che il volume occupato da una miscela di acqua e vino è leggermente inferiore alla somma dei volumi dei due liquidi separati; preferibile, però, ignorare questa bizzarria della natura, per non perdere l’occasione di elaborare un ragionamento troppo bello per essere accantonato.
2.3 Il volo fra due treni (Charles-Ange Laisant, 1906)
Due treni che si trovano sullo stesso binario si mettono contemporaneamente in moto, dirigendosi uno contro l’altro, il primo alla velocità di 40 km/h, il secondo alla velocità di 60 km/h. Nello stesso istante una mosca che si era adagiata sulla locomotiva del primo treno, si mette a volare in direzione dell’altro treno a una velocità di 80 km/h. Appena arriva a toccarlo, inverte istantaneamente il proprio senso di marcia e torna verso il treno di partenza. Toccato anche questo treno, inverte di nuovo il senso di marcia e continua a procedere così, avanti e indietro, da un treno all’altro finché questi non si scontrano. Sapendo che, alla partenza, la distanza tra i due treni era di 100 km, quanto spazio avrà percorso in tutto la mosca, dall’inizio del volo al momento della collisione?
■ Soluzione. Non è assolutamente consigliabile tentare di risolvere il problema seguendo nei dettagli l’azione descritta. La soluzione può essere trovata in maniera molto più semplice, concentrandosi solo sulla situazione finale e considerando, in particolare, che lo scontro tra i due treni avverrà esattamente un’ora dopo la loro partenza. Trascorsa un’ora, infatti un treno avrà percorso 40 km e l’altro 60 km, annullando così la distanza di 100 km (40 + 60 = 100) che li divideva all’inizio. Di conseguenza, dato che la mosca ha viaggiato alla velocità di 80 km/h, in un’ora avrà percorso 80 km.
2.4 La colletta (Anonimo, 1997)
Nel corso di una serata di beneficenza alla quale partecipano 100 persone, un certo numero di queste versa 100 euro a testa. Delle restanti persone, una metà versa 200 euro a testa, mentre l’altra metà non versa nulla. Quanti soldi vengono raccolti in tutto?
■ Soluzione. Questo problema sembrerebbe non ammettere una soluzione determinata, perché il suo enunciato non specifica il numero di persone che versa 100 euro a testa. In realtà può essere risolto facilmente considerando che, se la metà di un numero qualsiasi di persone versa 200 euro a testa e l’altra metà non versa niente, è come se ciascuna di loro versasse 100 euro (come tutte le altre). In definitiva, l’incasso totale è di: 100 × 100 euro = 10.000 euro.
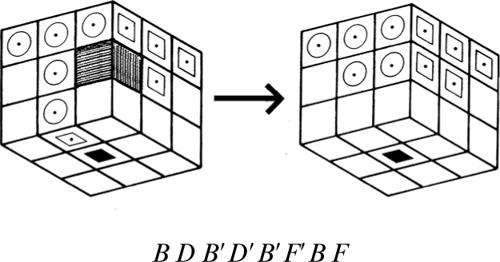
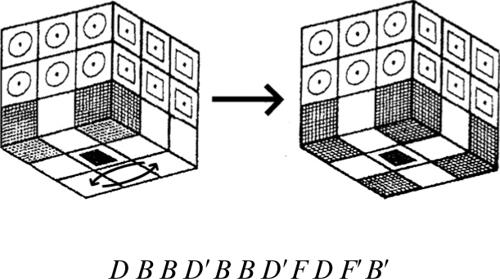
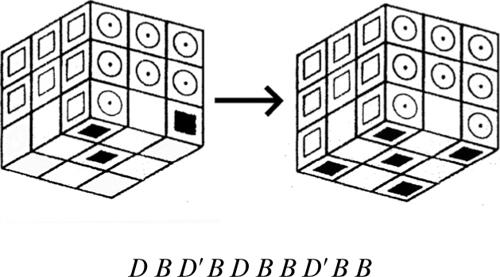
2.5 Il cubo di Serse (Anonimo, 2007)
Si narra che, dopo essere stato sconfitto dai greci a Salamina, il re persiano Serse si recò presso l’oracolo di Delfi portando in dono un cubo di piombo con la superficie esterna dorata. Egli chiese quali possibilità di vittoria avrebbe avuto, se avesse affrontato il nemico ancora una volta. L’oracolo gli rispose: «Taglia il cubo in 27 cubetti uguali e mettili in una borsa. Poi estrai un cubetto a caso e fallo rotolare; se si ferma con una faccia d’oro rivolta verso l’alto, la tua prossima campagna avrà successo». Quali erano le probabilità di vittoria di Serse?
■ Soluzione. Si può pensare di risolvere questo problema analizzando in dettaglio le caratteristiche dei vari cubetti ottenibili. In maniera più rapida, però, si può trovare la soluzione, effettuando il seguente, semplice ragionamento:
• in totale, le facce di 27 cubi sono: 6 × 27 = 162;
• le facce dorate sono solo: 9 × 6 = 54;
• di conseguenza, le probabilità di uscita di una faccia dorata sono: 54/162 = 1/3.
■ Nota. Storicamente, il desiderio di rivalsa del re Serse venne definitivamente soppresso, nel giro di una settimana, da altre due cocenti sconfitte infertegli dai greci (a Platea, il 20 agosto del 479 a.C., e a Micale, il 27 agosto del 479 a.C.).
3. Enigmi ingannevoli
Problemi risolubili in maniera relativamente semplice, ma il cui enunciato induce il solutore a fornire una risposta errata oppure lo trae in inganno impedendogli di trovarla.
3.1 La lumaca rampicante (Manoscritto di Bakhshali, 700 ca d.C.)
Il manoscritto di Bakhshali è un antico manoscritto matematico redatto su fogli di corteccia di betulla e ritrovato nell’estate del 1881, nei pressi del villaggio di Bakhshali (oggi in Pakistan). Andato distrutto in larga parte, ne sono sopravvissuti solo 70 fogli. Contiene regole e tecniche per risolvere problemi aritmetici, algebrici e geometrici. La sua data di origine è molto incerta, anche se in genere è collocata intorno al 700 d.C. In esso è possibile leggere il problema della lumaca rampicante.
Una lumaca intende arrivare in cima a un muro alto 7 metri; durante il giorno sale di 4 metri, ma nel corso della notte scivola indietro di 3 metri. Dopo quanti giorni, dall’inizio della scalata, riuscirà a raggiungere la sommità del muro?
■ Soluzione. In pratica, la lumaca sale di 1 metro ogni 24 ore; quindi si è istintivamente portati a concludere che le siano necessari 7 giorni per attivare in cima al muro (alto 7 metri). In realtà, se così fosse, all’alba del quinto giorno, partendo da 4 metri di altezza, non avrebbe la possibilità di salire per altri 4 metri, in quanto il tratto di muro rimasto, ne misurerebbe solo 3. La lumaca, quindi, riuscirà ad arrivare in cima al muro al termine del quarto giorno, salendo di 4 metri dopo essere partita da un’altezza di 3 metri (a quel punto, trovandosi sulla sommità del muro, non dovrebbe più scivolare indietro, di notte).
3.2 Gatti e topi (Italo Ghersi, 1913)
Un gatto e mezzo mangiano un topo e mezzo, in un minuto e mezzo. Quanti gatti occorrono per mangiare 60 topi in 30 minuti?
■ Soluzione. L’enunciato del problema induce a pensare che il tempo occorrente per mangiare i topi dipenda dalla quantità di gatti. In realtà, il tempo impiegato da un gatto per mangiare un topo non è influenzato dall’eventuale presenza di altri gatti. Di conseguenza, se 1,5 gatti mangiano 1,5 topi in 1,5 minuti, vuol dire che, nello stesso lasso di tempo, una generica quantità X di gatti mangia un’uguale quantità X di topi. In particolare, un solo gatto mangia un solo topo in 1,5 minuti. Quindi, in 30 minuti, un solo gatto mangia: 30/1,5 topi = 20 topi. Per mangiarne 60 (il triplo) nello stesso tempo, occorrono 3 gatti.
3.3 Il paradosso della scatola (Joseph Bertrand, 1889)
Si hanno tre scatole identiche per forma e colore; una contiene due monete d’oro, un’altra due monete d’argento e la terza una moneta d’oro e una d’argento. Si chiudono le tre scatole e si dispongono su un tavolo in un ordine qualsiasi; poi, se ne sceglie una a caso e si preleva da questa una moneta, senza guardare l’altra. Se la moneta estratta è d’oro, qual è la probabilità che anche l’altra sia d’oro?
■ Soluzione. Avendo estratto una moneta d’oro, non è possibile che la scatola scelta sia quella che conteneva due monete d’argento; di conseguenza, questa poteva contenere o due monete d’oro o una moneta d’oro e una d’argento. Siccome queste due possibilità sono equivalenti, viene spontaneo attribuire il valore di 1/2 alla probabilità che nella scatola sia rimasta una moneta d’oro. Un tale deduzione, però, è erronea.
Per trovare la soluzione corretta, conviene denominare le tre monete nel seguente modo:
• O1 e O2: le due monete d’oro che si trovano nella stessa scatola;
• A1 e A2: le due monete d’argento che si trovano nella stessa scatola;
• O3: la moneta d’oro che si trova nella scatola con quella d’argento;
• A3: la moneta d’argento che si trova nella scatola con quella d’oro.
Relativamente a tale convenzione, la moneta d’oro estratta può essere:
• O1 e, in questo caso, l’altra moneta è d’oro (O2);
• O2 e, in questo caso, l’altra moneta è d’oro (O1);
• O3 e, in questo caso, l’altra moneta è d’argento (A3).
Siccome, in due casi su tre, la moneta rimasta nella scatola è d’oro, la relativa probabilità è uguale a 2/3.
3.4 Il dollaro scomparso (Eugene P. Northrop, 1944)
Tre amici si recano al ristorante. Quando hanno terminato di mangiare, il cameriere presenta loro un conto di 30 dollari, ossia 10 dollari a testa. I tre protestano giudicando la somma troppo alta, ma alla fine accettano di pagare. Il cameriere riferisce la protesta al padrone del ristorante e questo, per quieto vivere, gli consegna 5 dollari da rendere ai tre clienti. Ma il cameriere (mariolo) si mette in tasca 2 dollari e restituisce solo 3 dollari. In pratica, i tre amici finiscono per pagare 27 dollari, ossia 9 dollari a testa. Aggiungendo i 2 dollari trafugati dal cameriere, la spesa totale ammonta a 29 dollari. Che fine ha fatto l’altro dollaro?
■ Soluzione. Se si accetta acriticamente l’impostazione del calcolo finale fornita dall’enunciato, questo problema (un piccolo capolavoro, nel suo genere) sembra proprio inestricabile. In realtà, i 2 dollari trafugati dal cameriere mariolo sono già compresi nei 27 spesi dai tre amici e non devono essere ulteriormente conteggiati. Per far tornare i conti, bisogna semplicemente sommare ai 27 dollari spesi (25 per il pranzo e 2 per il cameriere) i 3 riavuti indietro (27 + 3 = 30).
3.5 Il dilemma dei tre prigionieri (Martin Gardner, 1959)
Nel braccio della morte, tre prigionieri (Alfio, Berto e Carlo) aspettano di essere fucilati all’alba del giorno dopo. In onore del compleanno del re, però, è stato reso noto che uno dei tre verrà graziato. Il guardiano sa chi di loro avrà salva la vita, ma non lo può rivelare. Alfio, però, attanagliato dall’angoscia, gli dice: «Siccome solo uno di noi tre sarà graziato, almeno uno, tra Berto e Carlo, dovrà morire. Se mi dici il nome di chi sicuramente non si salverà, ti regalerò il mio orologio d’oro. In questo modo, non tradirai il tuo segreto, perché non svelerai chi sarà graziato». Il guardiano si fa convincere e gli riferisce che verrà giustiziato Berto. Come promesso, Alfio gli dona l’orologio e si sente un po’ più sollevato. Prima la sua probabilità di salvarsi era uguale a 1/3; ora che la questione riguarda solo lui e Carlo, è convinto che sia salita a 1/2. È corretto il suo ragionamento?
■ Soluzione. Siccome è sicuro che almeno uno degli altri due prigionieri sarà giustiziato, venire a sapere chi sarà dei due non fornisce alcuna informazione aggiuntiva. Di conseguenza, la probabilità che Alfio possa salvarsi resta uguale a 1/3, in quanto la risposta fornita dal guardiano non può modificare tale valore. È oggettivamente difficile accettare una tale affermazione, ma ci si può convincere della sua esattezza riflettendo sulla contraddizione a cui può portare il ragionamento di Alfio. Infatti, prima di conoscere la risposta del guardiano, lui avrebbe potuto pensare: «Se morirà Berto, resteremo in ballo solo io e Carlo e, quindi, la probabilità che io possa salvarmi è di 1/2. Ma se morirà Carlo, resteremo in ballo solo io e Berto e, quindi, anche in questo caso, la probabilità che io possa salvarmi è di 1/2. In definitiva, indipendentemente da chi degli altri due è destinato a morire, la probabilità che io possa salvarmi sale sempre a 1/2 e non è più di 1/3...».
■ Nota. L’intrigante meccanismo di questo problema ne ha generato diverse altre varianti. Una di queste è stata impiegata per mettere a punto il gioco finale della popolare trasmissione televisiva a premi statunitese, Let’s Make a Deal, condotta da Monty Hall. In quel contesto, il concorrente di turno veniva portato di fronte a una parete con tre porte chiuse; dietro una di queste si nascondeva un’auto di lusso, mentre dietro ognuna delle altre c’era una capra. In prima istanza, il concorrente veniva invitato a scegliere una delle tre porte (che, comunque, restava chiusa). Poi il conduttore apriva un’altra porta e mostrava, intenzionalmente, una capra. A quel punto, al concorrente veniva offerta la possibilità di cambiare la scelta iniziale, optando per l’altra porta rimasta chiusa. Col tempo, i telespettatori cominciarono a domandarsi se al concorrente convenisse cambiare la prima scelta o no. L’opinione più diffusa era che le due possibilità fossero equivalenti, in quanto alla fine restavano due soli casi, ugualmente probabili. In realtà, al concorrente conveniva cambiare la scelta. Nel 1990, un’autorevole redattrice della rivista «Parade», Marilyn vos Savant, pubblicò la risposta corretta al quesito, ma ricevette migliaia di lettere infuriate (molte delle quali, inviate da docenti di matematica) che l’accusavano di ignorare la teoria delle probabilità. Il caso finì in prima pagina sul «New York Times» e il problema acquistò in breve tempo una popolarità planetaria, arrivando addirittura a essere votato da una giuria di esperti come il più bel dilemma probabilistico del secondo millennio.
4. Paradossi matematici
Problemi che non contengono inganni nell’enunciato, ma la cui soluzione porta a un risultato alquanto diverso da quello che ci si poteva intuitivamente aspettare.
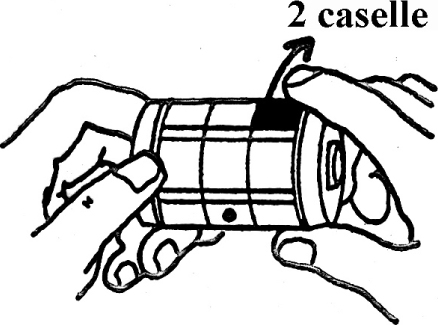
4.1 I chicchi sulla scacchiera (Leggenda persiana, 500 ca a.C.)
Il saggio Sussa ibn Dahir al-Hindi, inventore del gioco degli scacchi, venne invitato dal suo re Shiram a esprimere qualsiasi desiderio che sarebbe stato esaudito come ricompensa per la sua geniale invenzione. Egli chiese semplicemente del grano, la cui quantità sarebbe stata così calcolata: un chicco di grano sulla prima casella della scacchiera, più due chicchi sulla seconda, più quattro sulla terza e così via, raddoppiando ogni volta la quantità precedente, fino ad arrivare alla sessantaquattresima casella. Il re si meravigliò molto per l’entità apparentemente modesta di quella richiesta. Ma aveva ragione?
■ Soluzione. In realtà, la richiesta del saggio Sussa era tutt’altro che modesta. La quantità N di chicchi di grano da lui richiesta è uguale alla somma delle prime sessantaquattro potenze di 2, da 20 a 263, ovvero: N = 20 + 21 + 22 + 23 + ... +262 + 263.
Ricorrendo all’uso di una buona calcolatrice elettronica, ci si può rendere conto che questo numero vale circa 18,5 miliardi di miliardi (per la precisione: 18.446.744.073.709.551.615). Con una tale quantità di grano a disposizione, si potrebbe ricoprire tutta l’intera superficie terrestre (compresi mari, oceani, deserti e ghiacciai), collocando circa 3 chicchi e mezzo in ogni cm2. Un computer molto veloce, in grado di smistare un miliardo di chicchi al secondo, impiegherebbe più di 593 anni per riuscire a contarli tutti.
4.2 La corda intorno al mondo (William Whiston, 1702)
Si immagini di far passare intorno alla Terra una corda che abbia la stessa lunghezza dell’equatore (circa 40.000 km) e che, quindi, aderisca perfettamente al suolo in ogni punto. Si supponga, ora, di allungare di un metro questa corda e di sollevarla uniformemente, in modo che ogni suo punto abbia la stessa distanza dall’equatore. Quanto misurerà questa distanza?
■ Soluzione. Se si indica con C la circonferenza della Terra, all’equatore, il valore del relativo raggio R è dato dalla formula: R = C /2π. Nel caso in esame, se si indica con R′ il raggio in metri relativo alla circonferenza della corda allungata, si ha: R′ = (C + 1)/2π.
Siccome la distanza D cercata è uguale alla differenza di questi due raggi, si può porre:
Considerando che π ≈ 3,14, allora si ha: (1/2π) m ≈ (1/6,28) m ≈ 0,16 m ≈ 16 cm. Questo risultato è piuttosto sorprendente, perché intuitivamente si è portati a pensare che la distanza in questione debba essere uguale a pochissimi millimetri.
4.3 Sei gradi di separazione (Frigyes Karinthy, 1929)
Nel 1929, lo scrittore ungherese Frigyes Karinthy, in un proprio racconto, Catene, ipotizzò che ogni abitante della Terra può essere connesso a un altro suo simile attraverso una brevissima catena di conoscenze personali (amicizie, parentele, rapporti di lavoro ecc.) presumibilmente costituita da non più di sei livelli (e quindi da non più di cinque intermediari). Se si indicano i due soggetti da collegare con X, Y e i cinque intermediari, con A, B, C, D, E, una situazione del genere, può essere schematizzata nel seguente modo:
Nel 1967, il sociologo statunitense Stanley Milgram riuscì a dimostrare la veridicità di una tale teoria (denominata sei gradi di separazione), pianificando un esperimento concreto che coinvolse un folto gruppo di volontari.
Ma in che modo si può spiegare un simile risultato paradossale?
■ Soluzione. Si supponga che ogni abitante della Terra conosca almeno altri 50 suoi simili (cifra nettamente sottostimata). Sotto tale plausibile ipotesi, una persona qualsiasi è in grado di mettersi in contatto, attraverso tutte le proprie conoscenze, con almeno altre: 50 × 50 = 502 = 2.500 persone. Analogamente, attraverso le conoscenze di queste ultime, può mettersi in contatto con almeno altre 50 × 50 × 50 = 503 = 125.000 persone. Procedendo nello stesso modo, dopo appena sei di questi passaggi, le persone che può potenzialmente raggiungere diventano almeno: 50 × 50 × 50 × 50 × 50 × 50 × 506 = 15.625.000.000 (più del doppio della popolazione mondiale attuale).
■ Nota. Pur avendo la certezza che sia possibile mettere in contatto due persone qualsiasi attraverso una quantità estremamente bassa di contatti, resta il problema di riuscire a individuare la giusta concatenazione di intermediari. Da qualche anno, una ricerca del genere è diventata meno complessa, grazie al diffondersi su Internet di social network come Facebook.
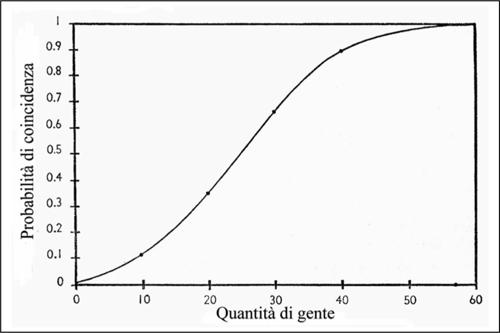
4.4 I compleanni comuni (Richard von Mises, 1939)
Qual è la probabilità che, in un gruppo di N persone, due di queste festeggino contemporaneamente il compleanno ossia che siano nate nello stesso giorno dello stesso mese, anche se in anni diversi?
■ Soluzione. Se si indica con Q(N) la probabilità che in un gruppo di N persone due di queste non festeggino il compleanno nello stesso giorno, si può calcolare che:
• se N = 2, Q(2) = 365 × 364/3652;
• se N = 3, Q(3) = 365 × 364 × 363/3653;
• se N = 4, Q(4) = 365 × 364 × 363 × 362/3654;
In generale, quindi, si ha:
Si può notare che, al crescere di N, il valore di Q(N) tende rapidamente a 0. Di conseguenza il valore della probabilità opposta (ossia che almeno due persone compiano gli anni nello stesso giorno) tende velocemente a 1, essendo dato da:
Il quadro completo della situazione è riassunto dal seguente diagramma, dove sull’asse delle ascisse sono riportati i valori di N e su quello delle ordinate sono riportati i valori di P(N).
Valori del genere sono veramente inattesi. Per esempio si stenta a credere che, in un gruppo di appena 50 persone, la probabilità in questione non è del 15%-20% (come si potrebbe intuitivamente pensare), ma arriva quasi al 100%.
■ Nota. Per comprendere meglio la natura di questo paradosso, può essere utile calarsi in una situazione più familiare. Si pensi, per esempio, a una raccolta di figurine composta da 365 pezzi; qual è la probabilità di non trovare neanche un doppione, tra le prime 50 figurine acquistate? Chi non ha perso memoria dei propri passatempi fanciulleschi, dovrebbe convenire che un’eventualità del genere è estremamente improbabile.
4.5 Cifre iniziali dei numeri (Frank Benford, 1938)
Intorno al 1881 l’astronomo Simon Newcomb si accorse che le tavole dei logaritmi (utilizzate allora come strumento di calcolo veloce) erano molto più consumate nelle prime pagine che nelle ultime. Ciò lo indusse a supporre che, nella pratica quotidiana, i numeri inizianti con la cifra «1» fossero molto più numerosi degli altri. Questa osservazione venne ripresa circa mezzo secolo più tardi dal fisico Frank Benford che, nell’intento di verificare l’attendibilità di una tale ipotesi apparentemente bizzarra, cominciò a raccogliere una grande mole di dati dalla natura più disparata. Al termine delle sue indagini, nel 1938, arrivò a formulare una legge di distribuzione della prima cifra significativa, relativa a un insieme di numeri generati casualmente in un contesto reale. Tale legge assegna le seguenti percentuali di frequenza alle nove cifre diverse da zero.
Come si può notare, non solo la frequenza della cifra «1» è nettamente predominante, ma quella relativa alle cifre successive assume un regolare andamento decrescente.
Ma in che modo si può spiegare un simile risultato paradossale?
■ Soluzione. Ovviamente le percentuali di distribuzione rilevate da Benford non sarebbero valide se si prendessero in considerazione tutti i numeri interi compresi tra 1 e infinito: in questo caso infatti ogni potenziale prima cifra sarebbe equamente rappresentata. Siccome però i numeri con cui abbiamo a che fare nella realtà quotidiana hanno sempre un valore finito e vengono spesso generati in ordine crescente, si può comprendere come mai quelli che iniziano con una cifra di basso valore possano avere maggiore probabilità di essere generati rispetto agli altri. Per esempio, mentre questo paragrafo è ancora in fase di stesura, non è possibile conoscere la connotazione precisa che assumerà alla fine. Però si può prevedere che, elencando i valori relativi alla lunghezza in lettere delle sue parole, quelli che presenteranno la cifra «1» al primo posto saranno in netta maggioranza (chi ne avrà voglia, potrà verificarlo). Infatti, oltre alle parole composte da una sola lettera, contribuiranno a incrementare un tale insieme anche tutte quelle che conterranno più di 9 lettere e meno di 20.
■ Nota. La legge di Benford non costituisce solo un’intrigante curiosità matematica, ma si presta anche a delle interessanti applicazioni pratiche. Per esempio, negli usa viene utilizzata per scovare gli evasori fiscali: tutte le dichiarazione dei redditi i cui importi non presentano un’adeguata distribuzione delle prime cifre vengono considerate sospette e sottoposte a un controllo più accurato. Si narra che, in un accertamento del genere, fosse incappato anche Bill Clinton, prima di diventare presidente degli usa.
5. Percorsi logici
Questi problemi possono essere risolti attraverso una sequenza di ragionamenti puramente logici, senza dover eseguire complessi calcoli matematici.
5.1 Lupo, capra e cavolo (Alcuino di York, 800 ca)
Alcuino di York mise a punto nel 789 d.C. il trattato di didattica matematica Propositiones ad acuendo iuvenes, destinato ai giovani allievi delle scuole carolingie. Per il proprio contenuto, incentrato essenzialmente su 56 problemi di natura giocosa, è considerato il più antico trattato dedicato alla matematica ricreativa. Alcuino di York propose il problema del lupo, della capra e del cavolo.
Un contadino viaggia con un lupo, una capra e un grosso cavolo. Arrivato sulla sponda di un fiume, vorrebbe traghettare tutto il suo carico dall’altra parte, ma dispone solo di una piccola barca sulla quale, oltre a lui, può prendere posto soltanto o il lupo, o la capra, o il cavolo. Il contadino sa che se lascia il lupo da solo con la capra quest’ultima verrà mangiata dal lupo; allo stesso modo, allontanandosi dalla riva solo con il lupo, il cavolo verrà divorato dalla capra. Come deve organizzare i traghettamenti per riuscire nel proprio intento, facendo in modo di non lasciare mai la capra da sola con il cavolo, o il lupo da solo con la capra?
■ Soluzione. La sequenza di azioni che il contadino deve compiere per salvare capra e cavoli può essere ricavata abbastanza facilmente, effettuando di volta in volta l’unica mossa consentita che non riporti alla situazione precedente.
La successione di mosse che risolve il problema è presentata nella seguente tabella (dove il pallino indica il contadino e le abbreviazioni Ca, Cv e Lu, indicano rispettivamente: la capra, il cavolo e il lupo).
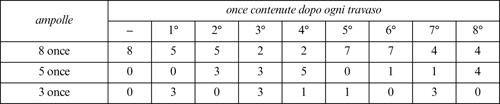
5.2. I travasi (Paolo dell’Abbaco, 1360 ca)
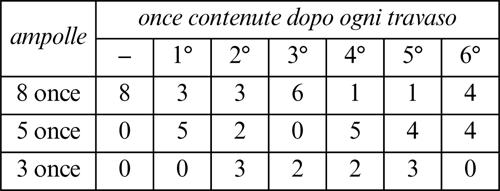
Si hanno a diposizione tre ampolle: la prima da 8 once, la seconda da 5 e la terza da 3. La prima ampolla è piena d’olio, mentre le altre due sono vuote. Qual è il minor numero di travasi che consente di avere al termine 4 once di olio nella prima e nella seconda ampolla?
■ Soluzione. Per risolvere questo problema, è necessario procedere per tentativi. Di volta in volta bisogna prendere in considerazione tutti i travasi effettuabili, scartando quelli che riportano a situazioni precedenti, finché non si riesce a ricavare la configurazione cercata.
Qui di seguito è riportato la tabella che schematizza la soluzione fornita da Paolo dell’Abbaco, composta da otto travasi.
■ Nota. Esiste una soluzione composta da soli sei travasi (sfuggita a Paolo dell’Abbaco), che può essere schematizzata con la seguente tabella.
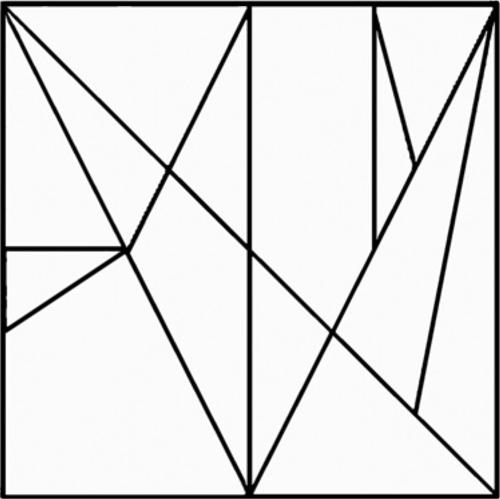
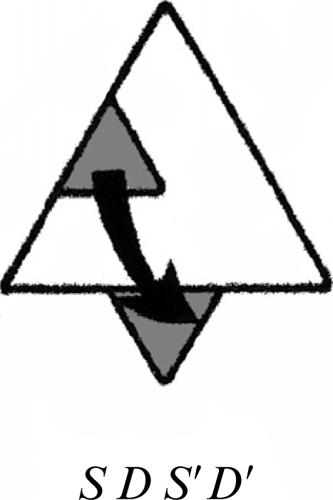
5.3 I ponti di Königsberg (Eulero, 1736)
La città di Königsberg (oggi Kaliningrad) è attraversata dal fiume Pregel, all’interno del quale sorgono due isolette. All’inizio del Settecento a cavallo di questo fiume erano stati eretti sette ponti che consentivano di effettuare tutti i vari collegamenti tra una riva e l’altra.
Durante le rituali passeggiate domenicali, gli abitanti del luogo si divertivano a cercare un percorso continuo che consentisse di transitare sopra tutti i ponti, senza mai ripassare su alcuno di essi. La questione appariva piuttosto semplice ma, nonostante gli innumerevoli tentativi effettuati, nessuno riusciva a risolverla.
A titolo d’esempio, nella seguente figura, è riportato un tracciato non valido, in quanto passa una seconda volta su uno dei due ponti che collegano le zone A e B.
Ma questo tipo di problema ammette almeno una soluzione, oppure no?
■ Soluzione. La questione arrivò alle orecchie di Eulero che, in quel periodo, si trovava in servizio presso la corte dell’imperatrice Caterina la Grande, a Pietroburgo. Per cercare di risolvere il problema Eulero mise a punto un nuovo strumento matematico, oggi chiamato grafo, costituito da un insieme di punti (nodi) e di linee (rami) che li connettono tutti o in parte.
A tale riguardo coniò le seguenti definizioni:
• un nodo è detto pari se in esso converge un numero pari di rami; al contrario, è detto dispari se in esso converge un numero dispari di rami;
• un grafo viene detto percorribile se può essere percorso in maniera continua, senza mai ripassare su uno stesso tratto.
Per stabilire la percorribilità di una rete, basta analizzare la natura dei suoi nodi: se sono tutti pari o solo due sono dispari, la rete è percorribile, altrimenti no.
Questo assunto si può giustificare considerando che in un nodo pari convergono tanti rami di arrivo quanti sono quelli di partenza, mentre uno dei rami collegato a un nodo dispari rimane necessariamente non accoppiato. Di conseguenza, un nodo dispari può costituire soltanto o un punto di partenza o uno di arrivo. Siccome nel tracciare una figura si può avere un solo punto di partenza e un solo di arrivo, non è possibile percorrere dei grafi che possiedono più di due nodi dispari.
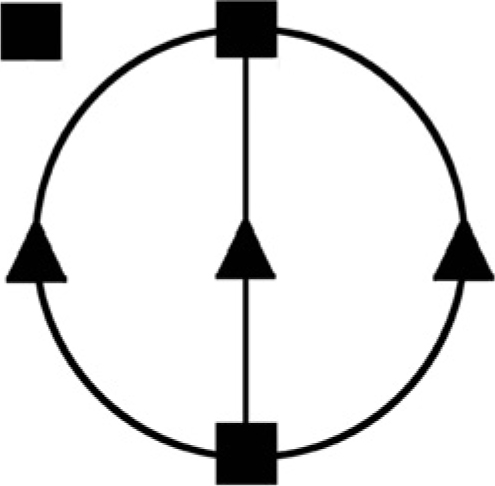
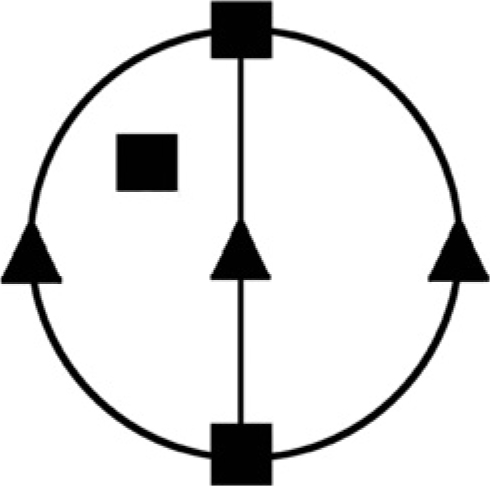
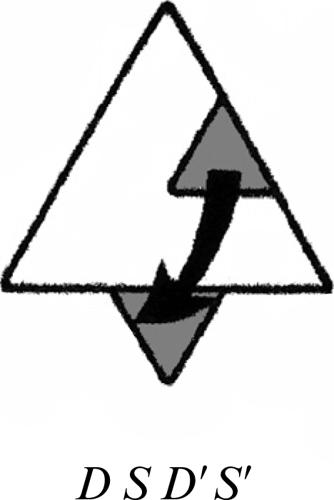
Per esempio, il seguente grafo possiede quattro nodi dispari e quindi non è percorribile.
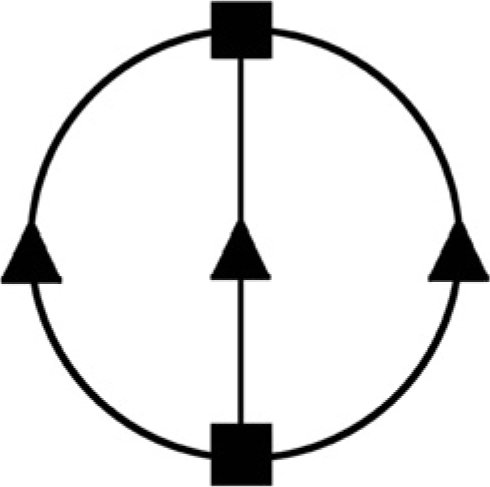
Invece il seguente grafo possiede due soli nodi dispari (quelli posti in basso) e, quindi, può essere percorso (purché si parta da uno di questi due nodi).
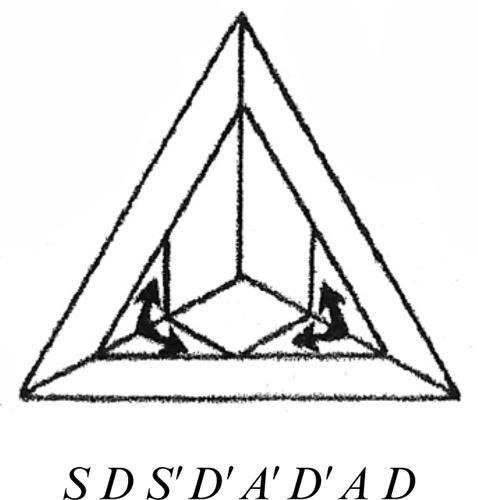
Sulla base di tali concetti Eulero schematizzò la pianta della cittadina, raffigurando ogni zona di terra con un punto e ogni ponte con un ramo. In questo modo ottenne una configurazione analoga alla seguente.
Quindi dimostrò che il problema in questione non è risolvibile, in quanto i quattro nodi del grafo da esso derivato sono tutti dispari.
■ Nota. Il problema dei ponti di Königsberg è all’origine della teoria dei grafi e costituisce uno dei primi problemi di topologia. In particolare, il confronto fra la pianta della cittadina di Königsberg e la raffigurazione del grafo che la schematizza è un primordiale esempio di come la topologia prescinda dalla forma rigida degli oggetti che studia.
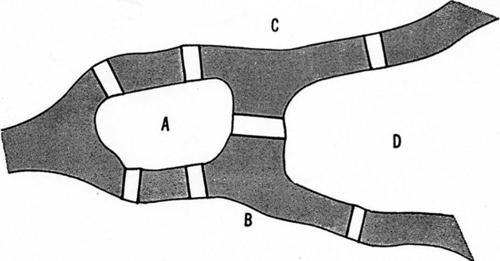
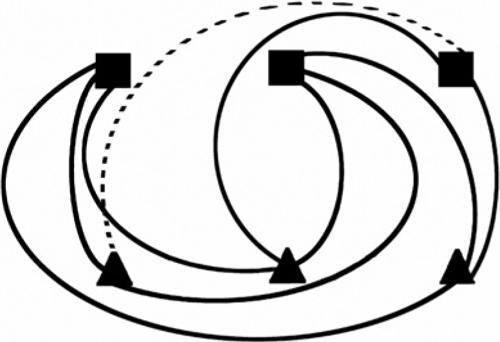
5.4 Acqua, luce e gas (Henry Dudeney, 1913)
Su un appezzamento di terreno sono state costruite tre nuove case, ognuna delle quali deve essere allacciata a tre diverse centrali di approvvigionamento (rispettivamente di acqua, luce e gas). Come è possibile effettuare tutti i collegamenti necessari facendo in modo che nessuno dei relativi tracciati si sovrapponga a un altro?
La seguente figura (dove ogni casa è rappresentata da un quadratino e ogni centrale da un triangolino) riproduce un tentativo di soluzione non valido, in quanto l’ultima linea di connessione (quella tratteggiata) ne incrocia un’altra.
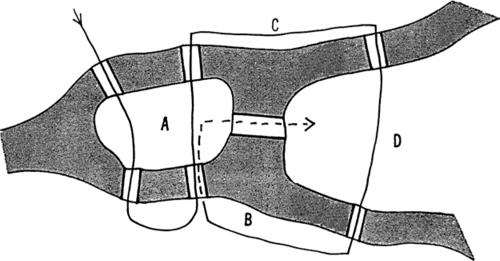
■ Soluzione. Questo problema non ammette soluzioni perché inevitabilmente, nell’effettuare i vari collegamenti richiesti, ci si ritrova a dover unire due punti che si trovano uno all’interno e un altro all’esterno di una curva chiusa. Come afferma un fondamentale teorema topologico (ma come è anche facile intuire, con un po’ di buon senso) non è possibile tracciare una linea che connetta due punti del genere senza essere costretti a intersecare la curva.
Per capire come mai non sia possibile sfuggire a tale situazione, conviene affrontare il problema senza assegnare una posizione prestabilita alle case e alle centrali, ma disponendole in modo da ottenere una struttura dai collegamenti più schematica possibile.
Per prima cosa si può osservare che, nel momento in cui si collegano due case a due centrali, si crea inevitabilmente una curva chiusa, come qui indicato.
Quando poi si congiunge ciascuna delle due case a tutte e tre le centrali, si generano necessariamente due curve chiuse aventi un tratto in comune, come qui indicato.
A questo punto, qualsiasi sia la posizione della terza casa, non ci sarà possibile connetterla a tutte le tre centrali senza passare su uno dei collegamenti già tracciati.
In assoluto le situazioni ipotizzabili sono solo due:
1. La casa si trova all’esterno di entrambe le curve chiuse, come nell’esempio qui riportato.
In tal caso, non è possibile collegare la casa alla centrale posta sul tratto interno delle due curve senza intersecare uno degli altri due tratti.
2. La casa si trova all’interno di una curva chiusa, come nell’esempio qui riportato.
In tal caso, non è possibile collegare la casa alla centrale posta sul tratto più esterno della seconda curva senza intersecare uno degli altri due tratti.
In questo modo sono state prese in considerazione tutte le possibili configurazioni derivabili dall’enunciato del problema. Qualsiasi altra potenziale configurazione è infatti riconducibile a una delle due precedenti mediante opportuni spostamenti delle case e delle centrali e conseguenti deformazioni elastiche dei tratti di curva.
Di conseguenza, si può affermare che il problema dato non ammette alcuna soluzione (almeno nello spazio a due dimensioni).
5.5 Alice & Bob (Ron Rivest, 1978)
Bob vuole inviare un oggetto a Alice. È un oggetto privato e non deve essere aperto da nessuno se non da lei. Decide di spedirlo in una scatola di metallo, ma l’unico modo per chiuderla è di usare un lucchetto. Scambiarsi le chiavi sarebbe troppo pericoloso. Entrambi dispongono solo di lucchetti. Come può Bob essere sicuro che la scatola possa essere aperta solo da Alice?
■ Soluzione. Nel modo più efficace e rapido, l’invio riservato segreto può essere effettuato mediante la seguente procedura:
• Bob chiude la scatola con un lucchetto e la invia ad Alice;
• Alice chiude la scatola con un altro lucchetto e la rispedisce a Bob;
• Bob rimuove il proprio lucchetto e rispedisce la scatola ad Alice;
• Alice riceve la scatola (ora protetta solo dal lucchetto apposto da lei) e la apre con facilità.
Nei vari tragitti effettuati nessun altro può essere stato in grado di aprire la scatola, dato che non ci sono stati scambi di chiavi.
■ Nota. I nomi Alice e Bob sono usati spesso, nelle esposizioni scientifiche, per indicare dei personaggi invece di ricorrere alle semplici lettere A e B (che possono dar luogo a fraintendimenti). Questa usanza venne inaugurata dal matematico statunitense Ron Rivest nel 1978 (proponendo proprio il precedente problema), allo scopo di illustrare in termini divulgativi la logica su cui si basa il sistema di crittografia asimmetrica rsa, utilizzato per codificare delle informazioni con un alto grado di sicurezza.
6. Incasellamenti logici
Questioni riguardanti la sistemazione di un insieme di elementi all’interno di una matrice quadrata, nel rispetto di determinate condizioni iniziali.
6.1 Quadrati magici (Shu-Ching, ca 650 a.C.)
Il Shu-Ching è considerato il più antico testo storico cinese (Il libro della storia) e consiste in una vasta raccolta di discorsi, colloqui e brevi trattazioni politiche, attribuiti a vari sovrani e ministri. Non si occupa specificamente di matematica, ma descrive, per la prima volta, una configurazione numerica, analoga a quella del quadrato magico 3 ↔ 3.
Il quadrato magico consiste nell’inserire in una matrice quadrata di lato N > 1, gli N 2 numeri interi compresi tra 1 e N 2, facendo in modo che, sommando i numeri presenti in ogni riga, in ogni colonna e in entrambe le diagonali principali, si ottenga sempre lo stesso valore (detto costante magica).
■ Soluzione. Per N = 2, il problema proposto non ammette soluzioni.
Infatti, una matrice 2 × 2 contiene due righe, due colonne e due diagonali; di conseguenza per poterla riempire in base alle regole esposte, sarebbe necessario ottenere l’eventuale costante magica in sei modi diversi, come somme di due numeri interi, compresi tra 1 e 4. Le uniche somme ottenibili in tale modo, però, sono solo queste sei, non tutte uguali tra loro: 1 + 2 = 3; 1 + 3 = 4; 1 + 4 = 5; 2 + 3 = 5; 2 + 4 = 6; 3 + 4 = 7.
Per N = 3 esiste un’unica soluzione (a meno di rotazioni e ribaltamenti).
È possibile trovare rapidamente questa soluzione effettuando le seguenti considerazioni logiche:
• la somma dei nove valori da inserire, da 1 a 9, è uguale a 45;
• il quadrato contiene tre righe (e tre colonne), quindi il valore della costante magica deve essere necessariamente uguale a: 45/3 = 15;
• il valore medio dei nove numeri da utilizzare è: 45/9 = 5; quindi è opportuno inserire questo numero al centro della matrice per avere la possibilità di ottenere la costante magica nella maggiore quantità di modi possibile.
In effetti, adottando tale accorgimento, si può completare facilmente il riempimento della matrice, trovando i seguenti otto modi diversi di ottenere la costante magica: 4 + 9 + 2 = 15; 3 + 5 + 7 = 15; 8 + 1 + 6 = 15; 4 + 3 + 8 = 15; 9 + 5 + 1 = 15; 2 + 7 + 6 = 15; 4 + 5 + 6 = 15; 2 + 5 + 8 = 15.
Per N > 3 il riempimento delle matrici diventa abbastanza difficoltoso; in compenso però il numero delle configurazioni possibili aumenta notevolmente. In particolare, per N = 4 sono addirittura 880, contando anche tutte quelle ottenibili mediante rotazioni o ribaltamenti di altre.
A titolo d’esempio, qui di seguito è riportato il quadrato magico utilizzato dal pittore tedesco, Albrecht Dürer, nella propria incisione, Melancholia I. È interessante notare che i due numeri posti nelle caselle centrali dell’ultima riga formano il valore dell’anno in cui venne realizzata l’opera: 1514.
■ Nota. In base alle teorie esoteriche cinesi, la configurazione di dimensioni 3 × 3 (detta Lu Shu) riunisce in sé i principi che sono alla base della Vita e del Cosmo. I numeri pari corrispondono alla natura femminile dello Yin e quelli dispari alla natura maschile dello Yang. Il numero 5, al centro, rappresenta la Terra, mentre gli altri otto numeri, a coppie di due, simboleggiano i quattro elementi principali: il 4 e il 9 i metalli, il 2 e il 7 il fuoco, l’1 e il 6 l’acqua, il 3 e l’8 il legno. Venne spontaneo quindi attribuire allo Lu Shu dei poteri straordinari.
I magi di Persia, per esempio, lo incidevano su una lastrina d’argento che poi applicavano sulla parte malata di un infermo, convinti di poterlo guarire. Per tale motivo gli aggregati numerici di questo genere sono stati denominati quadrati magici.
L’arte di confezionare queste particolari alchimie matematiche affonda le proprie radici in tempi remoti. Una popolare leggenda cinese narra che, mentre era in meditazione sul Fiume Giallo, l’imperatore e filosofo Yu (vissuto intorno al 2200 a.C.) vide materializzarsi d’improvviso una tartaruga sul cui dorso erano incisi i numeri dall’1 al 9, disposti a forma di quadrato magico, di dimensioni 3 × 3 e di costante 15. Non esistono però documenti che comprovano tale racconto.
6.2 Quadrati latini e greco-latini (Eulero, 1782)
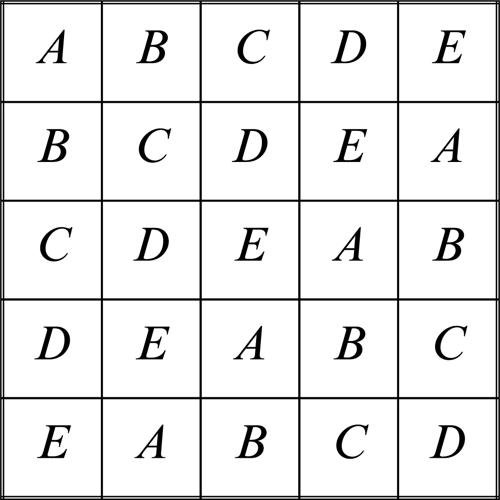
Per quadrato latino si intende una matrice quadrata di lato N, contenente N simboli diversi, ripetuti N volte e disposti nelle varie caselle in modo che nessuno di loro compaia più di una sola volta in ogni riga e in ogni colonna. Qui è riportato un semplice esempio di ordine 5.
Una variante più impegnativa di questo gioco è costituita dal quadrato greco-latino, che contiene in ogni casella due simboli (e non uno solo) disposti in modo che ognuno compaia una sola volta in ogni riga e in ogni colonna, e che ogni coppia di simboli sia presente una sola volta. Il nome di questa particolare configurazione deriva dal fatto che in passato venivano utilizzati come simboli le lettere degli alfabeti greco e latino. Qui di seguito è riportato un esempio di ordine 4, ma è possibile comporne altri di dimensioni maggiori.
■ Soluzione. Un modo per costruire un quadrato greco-latino consiste nel sovrapporre due opportuni quadrati latini ognuno dei quali costruito su un diverso insieme di N × N simboli.
Qui di seguito è riportato un esempio di ordine 5.
Stranamente, è possibile costruire dei quadrati greco-latini di un qualsiasi ordine N > 2, ma non di ordine 6.
■ Nota. Nel 1782, il matematico svizzero Eulero propose un gioco logico basato sulla costruzione di un quadrato greco-latino di ordine 6, noto come il Problema degli ufficiali. Il quesito chiedeva di disporre su una matrice quadrata 36 ufficiali appartenenti a 6 reggimenti diversi e con 6 gradi diversi in modo che in ogni riga e in ogni colonna fossero rappresentati tutti i reggimenti e tutti i ranghi. Eulero dimostrò che si possono costruire quadrati greco-latini di ordine N per ogni N dispari o multiplo di 4, congetturando che non fosse possibile farlo per N = 4K + 2, con K = 0, 1, 2... Nel 1901 il matematico francese Gaston Tarry verificò la correttezza della congettura di Eulero limitatamente al caso N = 6. Nel 1959 però, il matematico statunitense E.T. Parker e i suoi colleghi indiani, R.C. Bose e S.S. Shrikhande, provarono che l’ipotesi di Eulero era falsa per tutti i valori di N = 4K + 2, con N > 6. Per questo motivo vennero definiti i guastafeste di Eulero.
6.3 Le otto regine (Carl Friedrich Gauss, 1850)
Su una comune scacchiera 8 × 8, bisogna riuscire a collocare otto regine in modo che nessuna di esse possa venire catturata da una delle altre (ossia in modo che non vi sia mai più di una regina su una stessa linea parallela a uno dei lati della scacchiera o a una sua diagonale).
■ Soluzione. Un procedimento che consente di trovare alcune soluzioni analizzando in maniera sistematica le varie disposizioni possibili è il seguente:
• si colloca una regina nella prima casella in alto a sinistra;
• si procede poi collocando una regina per ogni riga nella prima casella verso sinistra che soddisfa i requisiti richiesti;
• se non è più possibile posizionare altre regine e non si è ancora arrivati a una soluzione, si sposti verso destra l’ultima regina collocata fino alla prima casella consentita, e si riprenda il procedimento;
• se non ci sono verso destra altre caselle consentite, si riporti la regina nella sua ultima posizione e si cerchi di spostare, con lo stesso criterio, quella che si trova nella riga immediatamente superiore;
• si proceda con gli stessi accorgimenti, finché non si arriva a una configurazione corretta.
A titolo d’esempio, qui di seguito è riportata una possibile soluzione, che presenta la singolare caratteristica di restare invariata, se viene ruotata di 180°.
■ Nota. Questo rompicapo è stato pubblicato per la prima volta su una rivista di scacchi nel 1848. Alla ricerca della sua soluzione si dedicò anche il matematico tedesco Carl Friedrich Gauss che nel 1850, dopo aver ideato il procedimento prima illustrato, riuscì a trovare tutte le 92 diverse soluzioni.
Con il nome di backtracking (letteralmente «seguendo le tracce all’indietro») il metodo ideato da Gauss è attualmente usato in informatica per la risoluzione di problemi di varia natura.
6.4 Quadrati alfamagici (Lee Sallows, 1986)
In ciascuna casella di una matrice quadrata 3 × 3 bisogna riuscire a inserire un diverso numero intero nel rispetto delle seguenti regole:
• la somma dei numeri disposti in ciascuna riga, colonna e diagonale deve fornire sempre lo stesso valore (come in un tradizionale quadrato magico);
• se si rappresenta ognuno dei nove numeri con il proprio nome in una determinata lingua (antica o moderna) e si sostituisce ciascuno di questi nomi con la quantità di lettere in esso contenuta, si deve ottenere di nuovo una struttura analoga a un tradizionale quadrato magico.
■ Soluzione. Questo problema presenta un alto grado di difficoltà e può essere affrontato solo con un programma per computer. A titolo di esempio, qui di seguito è riportata una soluzione in italiano.
■ Nota. I quadrati alfamagici sono stati inventati dall’esperto olandese di matematica ricreativa Lee Sallows. In una pubblicazione del 1986 presentò molti esempi di questo tipo composti in varie lingue (moderne, antiche e arcaiche...), tutti realizzati grazie a un programma per computer di sua ideazione, scritto in GW Basic. Mentre alcune lingue offrono un gran numero di possibilità diverse, l’unico esempio ottenibile in italiano, a meno di banali derivazioni, è quello sopra riportato.
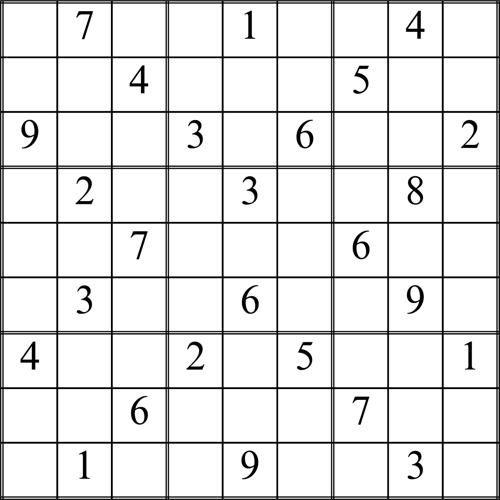
6.5 Sudoku (Howard Garnes, 1979)
Lo schema standard di un problema di Sudoku è formato da un quadrato di 9 × 9 caselle suddiviso in nove riquadri di formato 3 × 3. All’inizio alcune caselle sono riempite con dei numeri composti da una sola cifra. Il gioco consiste nel riempire tutte le altre caselle inserendo in ognuna di esse una cifra compresa tra 1 e 9 in modo che in ciascuna riga, in ciascuna colonna e in ciascun riquadro 3 × 3 uno stesso numero compaia una sola volta.
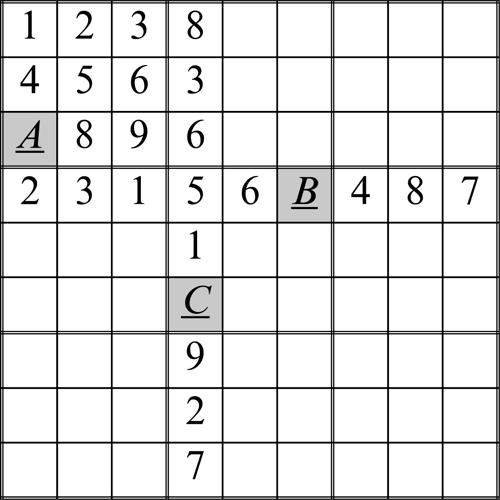
Consideriamo, per esempio, la situazione descritta nel seguente schema.
• Nella casella contrassegnata dalla lettera A può essere inserita solo la cifra 7, perché tutte le altre compaiono già nel relativo riquadro.
• Nella casella contrassegnata dalla lettera B può essere inserita solo la cifra 9, perché tutte le altre compaiono già nella relativa riga.
• Nella casella contrassegnata dalla lettera C può essere inserita solo la cifra 4, perché tutte le altre compaiono già nella relativa colonna.
Come si vede, le regole sono molto semplici; la ricerca di una soluzione corretta, però, richiede buone capacità di concentrazione.
Qual è il metodo migliore per risolvere un problema di Sudoku, nel modo più funzionale?
■ Soluzione. È possibile mettere a punto un metodo di risoluzione generale per i problemi di Sudoku basato sull’applicazione ripetuta di due soli tipi di ragionamento deduttivo:
• individuare in quale casella può essere inserita, con certezza, una data cifra;
• individuare quale cifra può essere inserita, con certezza, in una data casella.
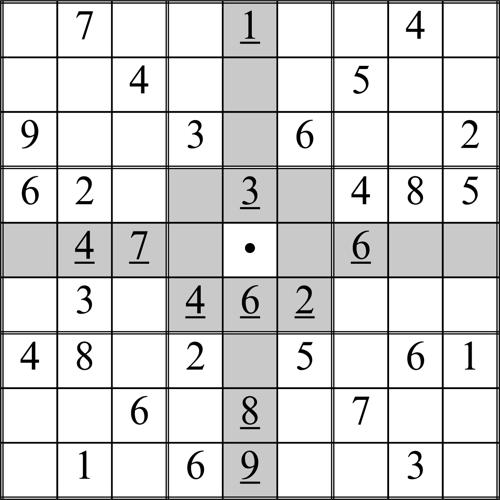
Un consiglio pratico per agevolare il primo tipo di ragionamento (individuare in quale casella può essere inserita, con certezza, una data cifra), consiste nel prendere in considerazione, di volta in volta, la cifra che compare in maggiore quantità nello schema. Per esempio si può notare che, nella seguente situazione, la cifra 6 compare quattro volte (mentre ognuna delle altre cifre al massimo tre).
Se per una visualizzazione più evidente si anneriscono tutte le righe e le colonne nelle quali la cifra 6 già compare, si può notare che nel primo riquadro della fascia centrale c’è una sola casella nella quale può essere inserita (evidenziata da un pallino nel seguente schema).
Il secondo tipo di ragionamento (individuare quale cifra può essere inserita, con certezza, in una data casella) è un po’ meno lineare dell’altro e, in genere, può essere messo in atto solo quando lo schema comincia a contenere un consistente numero di cifre.
Un consiglio pratico per applicarlo è nel prendere in considerazione, di volta in volta, la casella nella cui riga, nella cui colonna e nel cui riquadro compare globalmente la maggiore quantità di cifre diverse.
Si analizzi, per esempio, la casella evidenziata con un pallino nel seguente schema.
Si può notare che tutte le cifre, tranne la 5, compaiono globalmente almeno una volta nel relativo riquadro (2 − 3 − 4 − 6), nella relativa riga (4 − 7 − 6) e nella relativa colonna (1 − 3 − 6 − 8 − 9).
Di conseguenza, in quella determinata casella può essere inserita con certezza la cifra 5.
■ Nota. Nel 1979 un rompicapo molto simile al Sudoku venne messo a punto, con il nome di Number Place, dall’architetto statunitense Howard Garnes, ma l’idea non ebbe il successo sperato. Nel 1984 il gioco venne importato in Giappone dall’editore Nikoli, specializzato in pubblicazioni enigmistiche, ma neanche allora suscitò un grande interesse. Stranamente l’attenzione nei suoi confronti cominciò a imporsi dal momento in cui, due anni dopo, l’editore decise di pubblicare solo schemi con una disposizione simmetrica dei numeri.
Il Sudoku è stato importato in Occidente dal giudice neozelandese Wayne Gould, residente a Hong Kong, che racconta così la propria esperienza: «Nel 1997 mi trovavo in vacanza a Tokyo. Siccome sono un appassionato bibliofilo, un giorno sono entrato in una libreria. Ma non sapendo una parola di giapponese, ho comprato un libro di Sudoku, l’unico che conteneva solo numeri e non parole... Ho cominciato a risolvere quei problemi e non ho più smesso. A un certo punto, mi sono detto: se piace a me, forse divertirà anche altri. Allora ho acceso il computer e ho provato a costruire un software in grado di creare nuove griglie. Ma, essendo un programmatore dilettante, ho impiegato circa sei anni prima di riuscire nel mio intento...».
Nell’ottobre del 2004, Gould trovò il coraggio di bussare alle porte del «Times» di Londra, per proporre la pubblicazione dei primi problemi che aveva così realizzato. Da quel momento in poi il Sudoku cominciò a conoscere un successo incredibile, che si estese rapidamente a livello planetario.
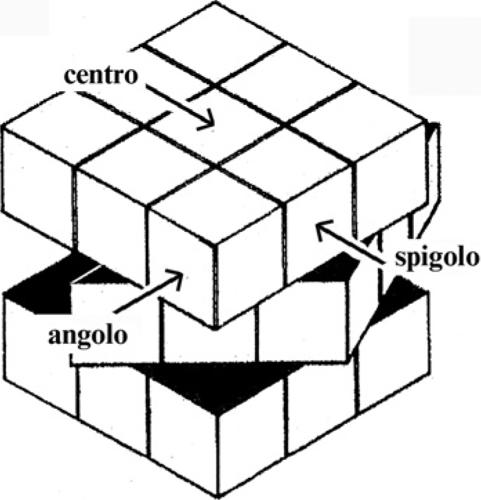
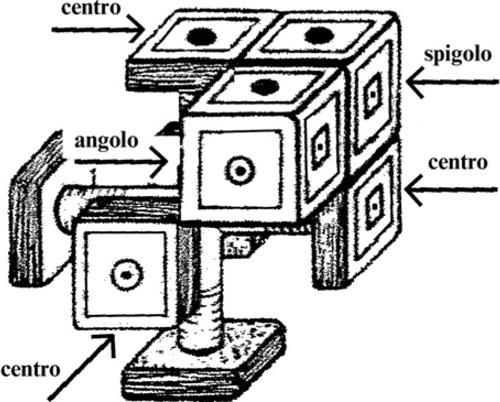
7. Rompicapi bidimensionali
Giochi di ragionamento che possono essere eseguiti solo manipolando degli opportuni elementi solidi, disposti in uno spazio a due dimensioni.
7.1 Stomachion (Archimede, ca 200 a.C.)
Il materiale di gioco è composto dal seguente insieme di 14 poligoni non regolari di vario formato (11 triangoli, 2 quadrilateri e un pentagono).
L’obiettivo principale consiste nel sistemare tutti i 14 pezzi senza sovrapposizioni, in modo da comporre un quadrato.
La particolare natura delle sagome a disposizione consente di ottenere anche numerose figure di fantasia (poligoni regolari, fiori, oggetti, animali ecc.) che possono indurre ulteriori problemi di ricomposizione.
■ Soluzione. Il nome di questo gioco, Stomachion («mal di stomaco» in greco) allude alla grande difficoltà della ricerca di una soluzione. In realtà un’impresa del genere è meno ardua di quanto si possa pensare perché è molto alta la quantità di diversi procedimenti attuabili per poterla portare a termine. In particolare nel 2003 il matematico statunitense Bill Cutler ha dimostrato che esistono ben 536 modi differenti di ottenere un quadrato utilizzando tutti i 14 pezzi (senza contare le soluzioni equivalenti per rotazione o riflessione).
Il modo più razionale per impostare la ricerca di una possibile soluzione consiste nel cominciare dalla ricostruzione della cornice esterna (come avviene per un comune puzzle). Quindi, per prima cosa, bisogna cercare di posizionare ai quattro vertici del quadrato dei pezzi che consentano di formare degli angoli retti (direttamente o mediante opportune combinazioni).
Un modo di applicare tale criterio, per esempio, può essere il seguente.
Una volta disposti i primi pezzi secondo la configurazione sopra indicata, non sarà difficile posizionare i pezzi rimanenti per completare il quadrato, come qui indicato.
■ Nota. Questo antico rompicapo era noto tra i romani con il nome di Loculus Archimedius. Ciò testimonia che la sua paternità è stata sempre attribuita al celebre matematico greco Archimede (287-212 a.C.). Nel 1998 si è avuta un’inoppugnabile conferma al riguardo: l’analisi ai raggi ultravioletti di una pergamena ritrovata nel 1906 nella biblioteca della Chiesa del Santo Sepolcro di Istanbul, ha fatto riaffiorare una trascrizione del x secolo di alcuni lavori di Archimede, tra i quali la descrizione dello Stomachion. Molto probabilmente, Archimede mise a punto un tale singolare strumento per verificare le grandi potenzialità dei meccanismi combinatori.
7.2 Solitario (Gottfried Wilhelm Leibniz, 1716)
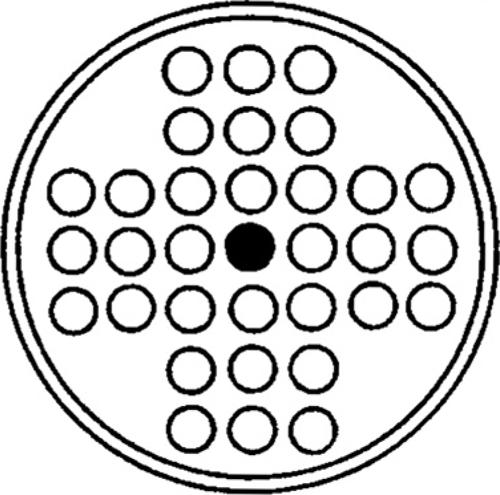
Il materiale di gioco è composto da 32 pedine e da un particolare tavoliere contenente 33 caselle disposte a croce. Inizialmente tutte le caselle, eccetto quella centrale, sono occupate da pedine.
L’unico tipo di mossa consentita si effettua con le seguenti modalità:
• una pedina può essere spostata, solo se si trova accanto a un’altra, contigua a una casella vuota;
• a partire da tali condizioni, è possibile trasferire la prima pedina nella casella vuota, saltando la seconda;
• la pedina saltata viene tolta dal tavoliere;
• una mossa può essere eseguita solo in orizzontale o in verticale (non in diagonale) e non è possibile scavalcare più di una pedina con un unico salto.
L’obiettivo principale consiste nel riuscire a eliminare tutte le pedine tranne una, posizionata al centro.
■ Soluzione. Ciascun potenziale percorso che consente di raggiungere la configurazione finale deve necessariamente essere composto da 31 mosse, dato che ognuna di esse consiste nell’eliminazione di una pedina. La ricerca di una possibile soluzione è però piuttosto impegnativa, perché non è facile riuscire a prevedere le ripercussioni finali che possono avere le mosse compiute all’inizio.
Il modo migliore di affrontare questo tipo di problema, quindi, consiste nel suddividerlo in due o più sottoproblemi meno complessi.
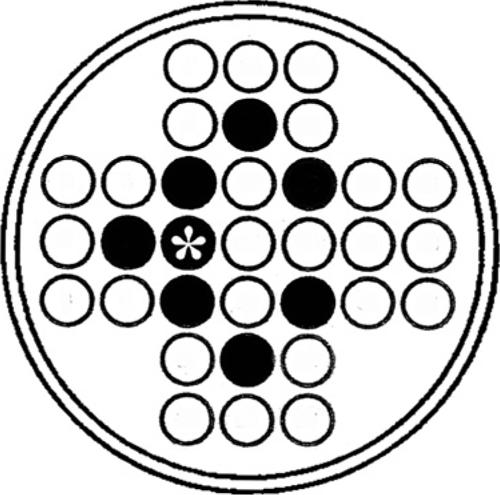
Per esempio si può osservare che, partendo dalla seguente situazione, è possibile arrivare a quella finale spostando circolarmente (in senso orario o antiorario) la pedina marcata con un asterisco.
Di conseguenza, si può impostare un possibile procedimento risolutivo cercando di compiere le prime mosse in modo da ottenere questa configurazione (e non direttamente quella finale).
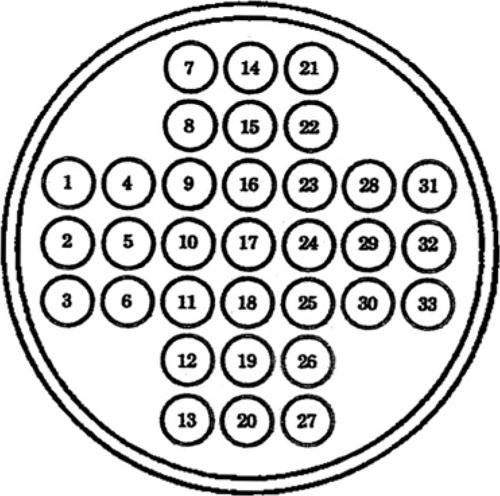
Qui di seguito viene riportata una soluzione che sfrutta un’impostazione del genere. Per rappresentarla in maniera sintetica, ogni casella del tavoliere è stata numerata in base alla seguente convenzione.
Ogni mossa da compiere è rappresentata mediante una coppia di numeri: il primo indica la casella di partenza della pedina che deve essere mossa, il secondo indica la casella di arrivo.
■ Nota. L’invenzione di questo rompicapo viene attribuita a un anonimo aristocratico francese che, rinchiuso nella Bastiglia per motivi politici all’inizio del xvii secolo, lo mise a punto utilizzando il materiale di un gioco di strategia noto come La volpe e le oche.
Successivamente il rompicapo si diffuse in Francia e in altre zone dell’Europa, attirando l’attenzione di insigni studiosi. In particolare, il filosofo e matematico tedesco Gottfried Wilhelm Leibniz in una lettera del 1716 scrisse: «Il gioco chiamato Solitario mi piace moltissimo; io lo gioco alla rovescia, vale a dire, anziché costruire una data figura spostando le pedine verso gli spazi vuoti e rimuovendo i pezzi via via sorpassati, come prescrivono le regole del gioco, ho trovato più interessante ricostruire ciò che era stato prima distrutto, facendo saltare alle pedine degli spazi vuoti e riempiendo tali spazi. In tal modo ci si può provare a costruire una data figura, cosa che deve sempre essere possibile, almeno per quelle figure che vengono distrutte nel corso del gioco ordinario. Ma a che scopo tutto ciò, vi chiederete. Rispondo: per perfezionare l’inventiva; giacché tutto ciò che si scopre con l’esercizio della ragione deve in qualche modo potersi costruire».
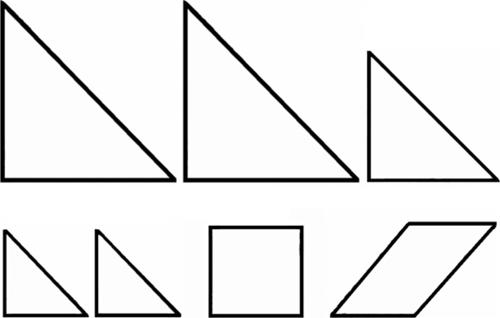
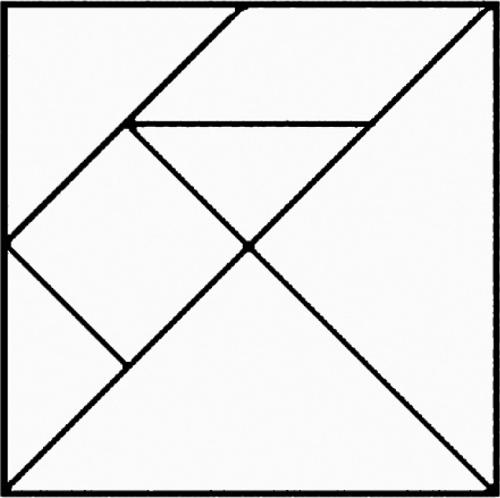
7.3 Tangram (Kan Chu Sen, 1721)
Il materiale di gioco è costituito dal seguente insieme di 7 poligoni (5 triangoli rettangoli, un quadrato e un parallelogramma).
L’obiettivo principale consiste nel sistemare tutti i 7 pezzi senza sovrapposizioni, in modo da comporre un quadrato.
Analogamente a quanto visto per lo Stomachion, la particolare natura delle sagome a disposizione consente di ottenere anche numerose figure di fantasia (poligoni regolari, fiori, oggetti, animali ecc.), che possono indurre ulteriori problemi di ricomposizione.
■ Soluzione. Data la minore quantità di pezzi rispetto allo Stomachion, la ricerca della soluzione di questo gioco potrebbe apparire meno complessa. Bisogna tener conto, però, che in questo caso esiste un solo modo di disporre i pezzi per ottenere un quadrato (senza contare le soluzioni equivalenti per rotazione, riflessione o scambio di due pezzi uguali). Anche in questo caso, comunque, il modo più razionale per impostare la ricerca di una possibile soluzione consiste nel cominciare dalla ricostruzione della cornice esterna, posizionando ai vertici del quadrato dei pezzi che consentano di formare degli angoli retti. A tale scopo verrebbe spontaneo utilizzare il pezzo quadrato, ma un’impostazione del genere impedirebbe di sistemare adeguatamente gli altri pezzi.
Un modo funzionale per compiere le prime mosse, può essere il seguente.
Una volta disposti i primi pezzi secondo la configurazione sopra indicata, non sarà difficile posizionare i pezzi rimanenti per completare il quadrato.
■ Nota. Un’antica leggenda giapponese sull’origine del Tangram narra di un monaco che donò a un proprio discepolo un quadrato di porcellana e un pennello, consigliandogli di viaggiare e dipingere sulla porcellana le bellezze che avrebbe incontrato nel proprio cammino. Il discepolo, emozionato, lasciò cadere il quadrato, che si ruppe in sette pezzi. Nel tentativo di ricomporre il quadrato, formò delle figure interessanti. Capì, da questo, che non aveva più bisogno di viaggiare, perché poteva rappresentare le bellezze del mondo solo con quei sette pezzi.
In realtà non si hanno notizie precise sull’origine del Tangram, né sul significato del suo nome. Pur essendo comunemente ritenuto di origine molto remota, le prime fonti conosciute che ne parlano risalgono al xviii secolo. In particolare viene citato nel libro giapponese Wakoku Chiyekurabe, una raccolta di problemi logici curata da Kan Chu Sen e pubblicata nel 1721.
In Occidente, il gioco apparve intorno al 1805. Uno dei primi testi in inglese che lo analizzò a fondo, The fashionable chinese puzzle, lo scrisse Lewis Carroll (l’autore di Alice nel paese delle meraviglie) e venne pubblicato a New York nel 1817.
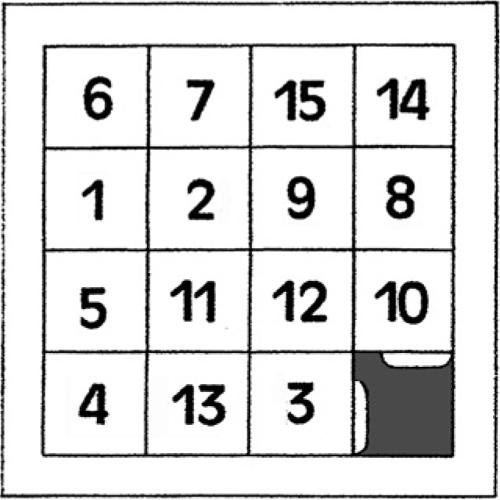
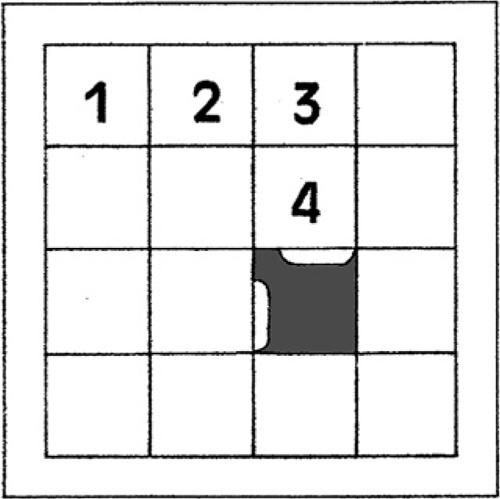
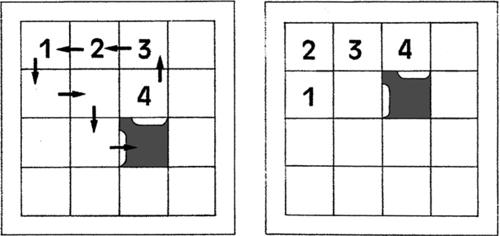
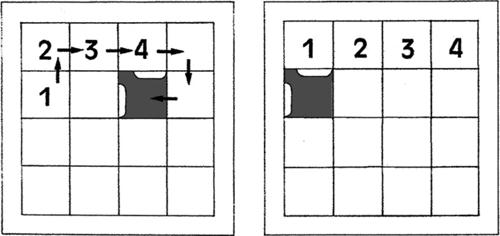
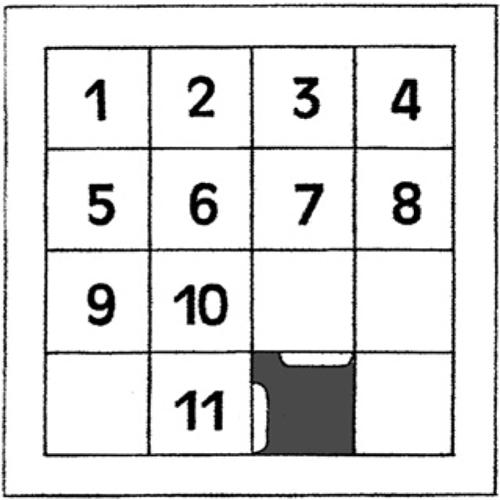
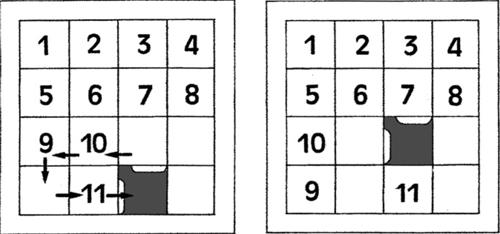
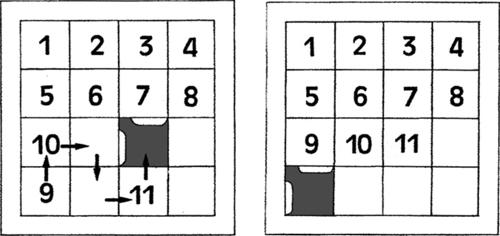
7.4 Il gioco del 15 (Samuel Loyd, 1879)
Il materiale di gioco è composto da un telaio quadrato all’interno del quale sono inserite 15 tessere numerate (da 1 a 15), sagomate in modo da poter essere agevolmente spostate (in orizzontale e in verticale) rimanendo sempre agganciate tra loro.
Partendo da una qualsiasi situazione disordinata (come, per esempio, quella precedente), l’obiettivo principale consiste nel riuscire a disporre in ordine crescente tutti i numeri riportati sulle tessere.
■ Soluzione. In teoria, il numero di permutazioni ottenibili con i 16 elementi costitutivi di questo rompicapo (considerando anche la casella vuota) è uguale a 16! Solo una metà di queste configurazioni, però, può essere potenzialmente ottenuta, spostando le tessere in maniera corretta. Infatti (come si può verificare praticamente), lo scambio di due tessere qualsiasi genera inevitabilmente lo spostamento di altre due; quindi è impossibile invertire solo le posizioni di due tessere, lasciando il resto immutato. L’insieme di tutte le potenziali permutazioni si suddivide dunque in due sottoinsiemi non collegati tra loro. In pratica, non è possibile passare da una configurazione appartenente a un dato sottoinsieme a una configurazione appartenente all’altro. Ne deriva, comunque, un numero di possibili configurazioni estremamente alto, dell’ordine di 1013.
Non è umanamente possibile prendere in considerazione tutte le potenziali soluzioni derivabili da ognuna delle possibili configurazioni di partenza. Per risolvere il gioco, a partire da una configurazione qualsiasi, bisogna quindi riuscire a mettere a punto delle manovre generali che consentano di posizionare opportunamente delle tessere, senza mettere in disordine quelle già sistemate. Il posizionamento di una tessera nella prima casella a sinistra di una riga si può effettuare con una certa libertà, perché le altre tessere della stessa riga non hanno ancora assunto posizioni vincolanti. Qui di seguito, vengono illustrate le manovre fondamentali che consentono di risolvere ogni altro tipo di situazione.
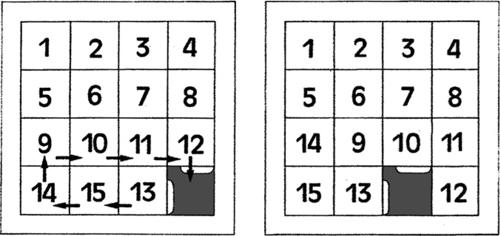
a) Per portare una tessera in una casella (dalla seconda in poi) appartenente a una delle prime due righe, conviene prima spostarla in una posizione che si trovi sotto la tessera da affiancare e sopra la casella vuota.
Se si spostano le tessere in base alle indicazioni del sottostante schema di sinistra, si ottiene la configurazione riportata in quello di destra.
A partire da questa nuova situazione, se si spostano le tessere in base alle indicazioni del sottostante schema di sinistra, si ottiene la configurazione desiderata, riportata in quello di destra.
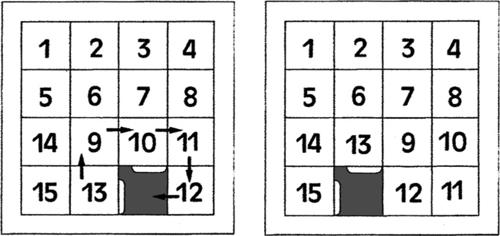
b) Per portare una tessera in una casella (dalla seconda in poi) appartenente alla terza riga, conviene prima spostarla in una posizione che si trovi sotto la tessera da affiancare e accanto alla casella vuota.
Se si spostano le tessere in base alle indicazioni del sottostante schema di sinistra, si ottiene la configurazione riportata in quello di destra.
A partire da questa nuova situazione, se si spostano le tessere in base alle indicazioni del sottostante schema di sinistra, si ottiene la configurazione desiderata, riportata in quello di destra.
c) Dopo aver completato le prime tre righe, l’assetto della quarta può assumere solo una di queste tre configurazioni: 13 − 14 − 15; 14 − 15 − 13; 15 − 13 − 14 (per i motivi analizzati in precedenza, infatti, le altre tre potenziali disposizioni non sono possibili).
Nel primo caso, il rompicapo è già risolto (fortunatamente!). Negli altri due casi, bisogna compiere una manovra un po’ delicata, dato lo stretto margine di azione a disposizione.
Si supponga, per esempio, che la situazione di partenza sia la seguente.
Se si spostano le tessere in base alle indicazioni del sottostante schema di sinistra, si ottiene la configurazione riportata in quello di destra.
A partire da questa nuova situazione, se si spostano le tessere in base alle indicazioni del sottostante schema di sinistra, si ottiene la configurazione, riportata in quello di destra.
A questo punto non è difficile completare l’ordinamento di tutte le tessere, facendo ruotare quelle delle ultime due righe, due volte, in senso antiorario.
Nel caso in cui le tessere dell’ultima riga siano disposte, invece, nell’ordine: 15 − 13 − 14, bisogna compiere una manovra analoga a quella appena vista, ma svolta in maniera simmetrica.
■ Nota. Questo rompicapo è stato ideato da Samuel Loyd, il più celebre enigmista statunitense del xix secolo. Per lanciare il gioco sul mercato, nel 1873, mise in palio un premio di 1000 dollari (una cifra da capogiro per quei tempi) a disposizione per chi fosse riuscito per primo a ordinare i quindici numeri in ordine crescente. Grazie a un sotterfugio beffardo, però, la versione da lui proposta presentava una posizione di partenza che rendeva impossibile la risoluzione del gioco. Le tessere erano tutte disposte in ordine crescente, tranne le ultime due (14 e 15) che erano invertite di posto. Come si è visto in precedenza, però, questa è una configurazione impossibile da ottenere.
Centinaia di migliaia di persone tentarono disperatamente di aggiudicarsi l’allettante premio. I giornali di allora registrarono più di 1500 casi di persone letteralmente impazzite, nel disperato tentativo di ricostruire un’inesistente soluzione che erano convinte di avere trovato, senza aver avuto l’accortezza di annotarla.
7.5 Asino rosso (John Harold Fleming, 1934)
Il materiale di gioco è costituito da dieci tasselli di forma e grandezza diversa, inseriti in una scatola rettangolare.
I tasselli possono essere spostati all’interno della scatola in orizzontale o in verticale, ma non possono essere né ruotati, né sollevati.
L’obiettivo principale consiste nel riuscire a liberare il tassello quadrato più grande (sul quale è disegnato un asino rosso), facendolo uscire attraverso la fessura posta in basso.
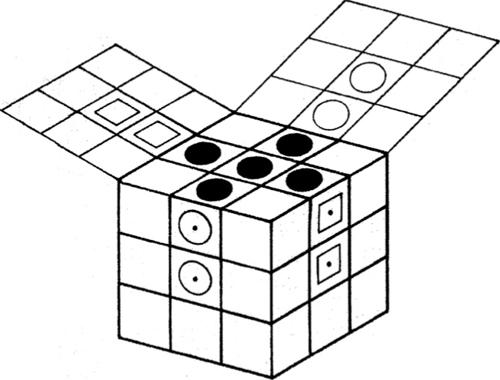
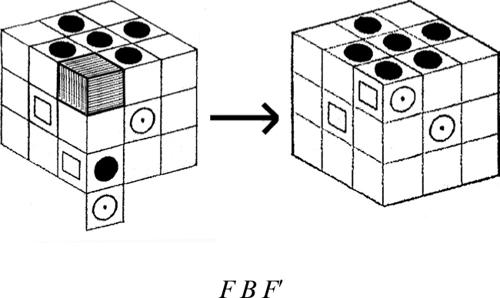
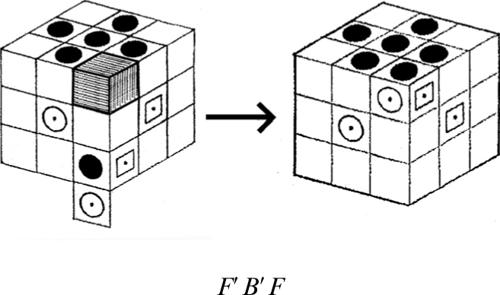
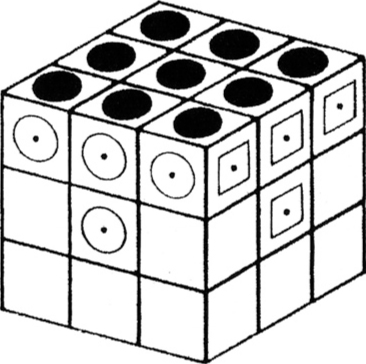
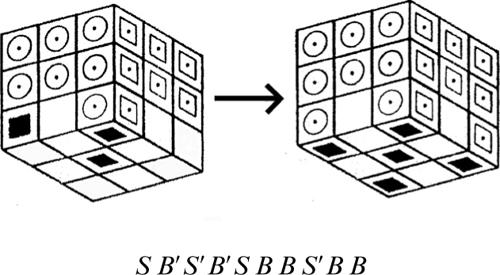
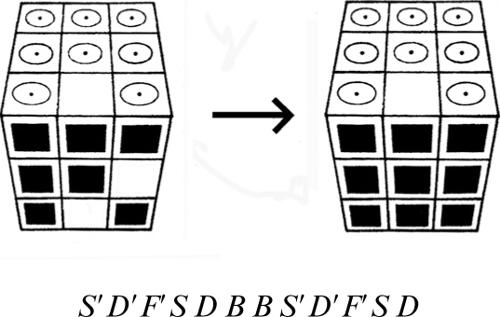
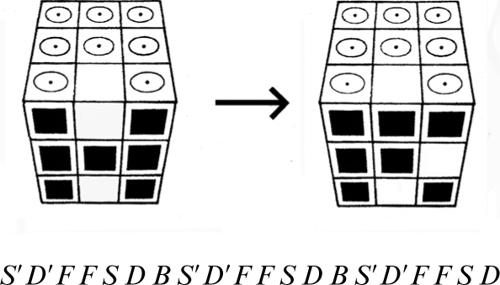
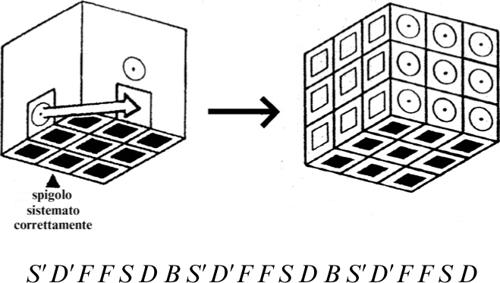
■ Soluzione. La ricerca di una possibile soluzione di questo rompicapo è alquanto impegnativa, soprattutto perché il numero di mosse richieste è piuttosto elevato. In particolare, nel 1964, il matematico inglese John Larmouth dell’Università di Cambridge ha dimostrato, con l’uso di un computer, che non è possibile risolvere il gioco compiendo meno di 81 mosse. Il modo migliore di affrontare questo tipo di problema, quindi, consiste nel suddividerlo, in due o più sottoproblemi meno complessi. Per esempio, si può osservare che per portare l’asino rosso in prossimità della fessura inferiore, è necessario prima spostare in alto i quattro tasselli rettangolari verticali (quelli che lasciano meno libertà di manovra), come indicato nella seguente figura.
Non è difficile verificare che, da questa situazione, si riesce a risolvere velocemente il gioco, facendo ruotare in senso antiorario i sei tasselli posti nella parte inferiore della scatola.
Di conseguenza, si può impostare un possibile procedimento risolutivo cercando di compiere le prime mosse, in modo da arrivare a una configurazione analoga alla precedente (e non direttamente a quella finale).
Qui di seguito, viene riportata una soluzione che sfrutta un’impostazione del genere. Per rappresentarla in maniera sintetica, ogni tassello del rompicapo è stato numerato in base alla seguente convenzione.
Ogni mossa prevista è indicata mediante il numero relativo al tassello da spostare. Se il movimento da compiere è obbligato, non sono riportate ulteriori specificazioni; altrimenti, se esistono delle potenziali alternative, viene specificata tra parentesi la posizione finale che il tassello deve raggiungere:
9 (al centro), 4, 5, 8 (in basso), 6, 10 (al centro), 8, 6, 5, 7 (in alto, a sinistra), 9, 6, 10 (a sinistra, in basso), 5, 9, 7, 4, 6, 10, 8, 5, 7 (in basso, a destra), 6, 4, 1, 2, 3, 9, 7, 6, 3, 2, 1, 4, 8, 10 (a destra, in alto), 5, 3, 6, 8, 2, 9, 7 (in alto, a sinistra), 8, 6, 3, 10 (a destra, in basso), 2, 9 (in basso, a destra), 1, 4, 2, 9, 7 (al centro), 8, 6, 3, 10, 9 (in basso), 2, 4, 1, 8, 7, 6, 3, 2, 7, 8, 1, 4, 7 (a sinistra, in alto), 5, 9, 10, 2, 8, 7, 5, 10 (in alto a sinistra), 2
■ Nota. L’origine di questo rompicapo è ignota, anche se alcuni esperti ritengono che derivi da un gioco thailandese denominato Khun Phaen. Non esiste, però, alcun tipo di documentazione a sostegno di tale tesi. All’inizio del xx secolo si sono diffusi in Occidente diversi rompicapi basati sullo spostamento di tasselli a volte simili nella struttura, a volte piuttosto differenti. La versione presentata in questo contesto, la più interessante in assoluto, è stata brevettata nel 1934 dall’enigmista inglese John Harold Fleming, ottenendo un largo successo in Europa e in particolare in Francia.
8. Rompicapi tridimensionali
Giochi di ragionamento che possono essere eseguiti solo manipolando appositi elementi solidi, disposti in uno spazio a tre dimensioni.
8.1 Torre di Hanoi (Édouard Lucas, 1883)
Il materiale di gioco è composto da una certa quantità di dischetti di diverso diametro, forati al centro, e da una tavola orizzontale, nella quale sono innestati tre pioli verticali. All’inizio tutti i dischetti vanno inseriti in uno dei tre pioli, in ordine di diametro decrescente verso l’alto (in modo che l’intera pila assuma una configurazione conica).
Il gioco consiste nello spostare i dischi su un altro piolo.
■ Soluzione. Si può spostare un solo disco alla volta, secondo le regole seguenti:
• dopo ogni mossa i dischi dovranno trovarsi tutti collocati su uno, due o tre pioli, sempre in ordine decrescente, dal basso al vertice;
• si può togliere il disco superiore di uno dei tre pioli per infilarlo in una colonnina vuota, senza dischi;
• è possibile togliere il disco superiore di uno dei tre pioli e spostarlo su un altro piolo, soltanto se il disco superiore di quest’ultimo è più grande di quello che viene spostato.
Da ciò ne deriva che il procedimento risolutivo deve consistere in un susseguirsi di manovre analoghe a quella qui di seguito descritta (denominando gli N dischetti, con un numero da 1 a N, in ordine di diametro crescente):
• si compone una pila con i dischetti da 1 a K (con K ≤ N − 1), liberando un piolo;
• si sposta il dischetto K + 1 nel piolo vuoto;
• si scompone la pila precedente;
• si compone una nuova pila con i dischetti da 1 a K + 1.
Alla luce di quanto esposto, si può intuire che il numero di mosse necessario per risolvere completamente il gioco cresce a dismisura all’aumentare di N. In particolare, è stato dimostrato che, per una torre composta da N dischetti, il minimo numero di mosse richiesto e uguale a: 2N − 1. Per esempio, con 4 dischetti le mosse minime sono: 24 − 1 = 16 − 1 = 15; con 8, arrivano a: 28 − 1 = 256 − 1 = 255.
Un metodo risolutivo molto semplice che garantisce il raggiungimento dell’obiettivo nel minor numero di mosse possibile, può essere così descritto:
• si sposta alternativamente il dischetto piccolo (n. 1), una mossa sì e una no, facendolo procedere sempre nello stesso senso (orario o antiorario), attorno ai tre pioli;
• subito dopo aver spostato il dischetto piccolo, si effettua l’unica mossa che può essere compiuta con un dischetto grande.
Questo procedimento è giustificato dalle seguenti osservazioni:
• dopo aver spostato un dischetto grande, si può muovere solo il dischetto piccolo (a meno di non compiere, inutilmente, la mossa opposta a quella appena effettuata);
• è controproducente spostare due volte di seguito il dischetto piccolo, perché in questo modo si altera la successione delle mosse necessarie per la composizione o la scomposizione di una pila;
• analogamente, non conviene muovere il dischetto piccolo nel senso opposto a quello della mossa precedente, perché ciò equivarrebbe a spostarlo due volte di seguito.
La seguente tabella mostra un’applicazione del metodo prima descritto, relativa a una pila composta solo da 4 dischetti.
Nella prima colonna, sono indicati i numeri progressivi delle mosse effettuate; nelle altre tre colonne sono riportate le situazioni relative ai tre pioli, indicati con A, B e C. In relazione a ogni mossa è evidenziato in neretto il numero del dischetto spostato.
■ Nota. Questo rompicapo è stato inventato dal matematico francese Édouard Lucas, che lo mise in commercio nel 1883 con lo pseudonimo di Prof. Claus del Collegio di Li-Sou-Stìan (anagrammi di Prof. Lucas del collegio di Saint Louis). Nel foglietto illustrativo il gioco veniva spacciato come la versione semplificata di una fantomatica Torre di Brahma, conservata in un tempio di Benares e composta da 64 dischi d’oro. Si affermava, al riguardo, che ai monaci di quel tempio era stato assegnato il compito di ricomporre l’intera torre, lavorando notte e giorno e spostando un disco al secondo; quando quest’opera sarà compiuta, il mondo scomparirà in un boato di tuono. Tutto sommato in merito a tale profezia si può stare abbastanza tranquilli. La quantità minima di mosse necessarie per raggiungere l’obiettivo stabilito è uguale a: 264 − 1, ovvero a un numero composto da 20 cifre, uguale a: 18.446.744.073.709.551.615. Quindi dovranno passare molte migliaia di milioni di anni prima che i monaci di quel tempio riescano a portare a termine il proprio incarico.
8.2 Cubo soma (Piet Hein, 1936)
Il materiale di gioco è costituito dal seguente insieme di 7 solidi irregolari (numerati convenzionalmente, nel modo indicato), ognuno dei quali composto da una diversa aggregazione non lineare di non più di 4 cubetti, tutti delle stesse dimensioni.
L’obiettivo principale consiste nel combinare i 7 pezzi in modo da comporre un cubo di dimensioni 3 × 3 × 3 cubetti. Analogamente a quanto visto per lo Stomachion e per il Tangram, la particolare natura delle sagome a disposizione consente di ottenere anche numerose figure di fantasia (scale, edifici, mobili, animali ecc.), che possono indurre ulteriori problemi di ricomposizione.
■ Soluzione. La soluzione di questo rompicapo non è molto impegnativa, essendo piuttosto ampia la varietà di procedimenti per portarla a termine. In particolare, nel 1961, il matematico inglese John Horton Conway ha dimostrato che esistono ben 240 modi differenti di ottenere un cubo utilizzando tutti i 7 pezzi (senza contare le soluzioni equivalenti per rotazione o riflessione).
Un ovvio accorgimento da seguire per impostare la ricerca di una possibile soluzione, consiste nel cercare di connettere all’inizio almeno due tra i pezzi 5, 6 e 7 (i più irregolari) e di sistemare solo alla fine il pezzo 1 (il più semplice da inserire).
Uno dei possibili modi per applicare un criterio del genere può essere così descritto.
Per prima cosa, si accostano i pezzi 5 e 7; a essi si affianca il pezzo 3 e, poi, si inserisce il pezzo 7 nello spazio superiore così creato. La seguente figura di sinistra indica in dettaglio il compimento di questa manovra, mentre quella di destra mostra la configurazione risultante.
Subito dopo, negli spazi così generati, si inseriscono i pezzi 2 e 6; solo alla fine, si sistema il pezzo 1. La seguente figura di sinistra indica in dettaglio questa manovra, mentre quella di destra mostra la configurazione risultante.
■ Nota. Questo rompicapo, inventato dal matematico e poeta danese Piet Hein, è stato commercializzato nel 1970 dalla Parker Brothers. L’autore lo aveva però ideato nel 1936, quando sentì parlare di uno spazio suddiviso in cubi durante una lezione di meccanica quantistica. In quel momento gli venne in mente che, prendendo le 7 forme irregolari che possono esser costruite combinando non più di quattro cubi tutti uguali, fosse possibile costruire un cubo di dimensioni più grandi.
8.3 Pyraminx (Uwe Mèffert, 1970)
Il materiale di gioco è costituito da un tetraedro regolare, suddiviso in 14 blocchetti mobili, collegati tra loro e sagomati in maniera tale che ciascuna delle 4 facce della piramide risulti scomposta in 9 faccette a forma di triangolo equilatero, colorate in 4 tinte diverse (per un totale di 4 × 9 = 36 faccette).
Partendo da una configurazione disordinata in cui le diverse faccette sono disposte in maniera casuale, l’obiettivo principale consiste nel rendere ogni faccia di colore uniforme, ruotando opportunamente i vari blocchetti mobili.
■ Soluzione. Per affrontare in maniera razionale la soluzione di questo rompicapo, è opportuno analizzare la struttura meccanica dell’oggetto da manipolare.
Come evidenziato dalla seguente figura, i blocchetti mobili sono di tre tipi diversi: angoli, supporti e spigoli.
In dettaglio, si contano:
• 4 angoli, ognuno dei quali mostra 3 faccette;
• 4 supporti, ognuno dei quali mostra 3 faccette;
• 6 spigoli, ognuno dei quali mostra 2 faccette.
Per quanto riguarda i potenziali movimenti, si può notare che:
• ogni angolo è imperniato sul sottostante supporto; quindi, può solo girare su sé stesso, senza spostarsi dalla propria posizione;
• ogni supporto è incernierato a una sferetta centrale; quindi, può solo ruotare intorno a essa, senza staccarsi dalla propria posizione;
• ogni spigolo è incastrato tra due diversi supporti, ma non è agganciato a essi; quindi, può cambiare la propria posizione, mediante l’effettuazione di opportune manovre.
Da quanto esposto, si deduce che le uniche mosse effettuabili sono le seguenti:
• ruotare un angolo su sé stesso;
• ruotare un insieme di blocchetti, composto da: un supporto, l’angolo a esso collegato e i tre spigoli appoggiati su di esso (strato triangolare);
• ruotare un insieme di blocchetti, composto da: tre supporti, i tre angoli a essi collegati e i tre spigoli appoggiati su di essi (strato trapezoidale).
In realtà, invece di muovere uno strato trapezoidale in un dato verso, è preferibile muovere nel verso opposto lo strato triangolare a esso complementare; questa mossa, infatti, è più agevole dell’altra.
Alla luce di queste osservazioni, è possibile ricavare un metodo risolutivo, rapido ed efficiente, che può essere descritto nel modo seguente.
☐ Si gira ciascuno dei 4 angoli, facendo coincidere i colori delle sue 3 facce con quelli del supporto sottostante; in questo modo, in ogni vertice di una faccia triangolare compare una sorta di rombetto di colore uniforme.
☐ Si ruotano opportunamente alcuni strati triangolari, facendo in modo che i 3 rombetti presenti ai vertici di ciascuna delle 4 facce della piramide siano tutti dello stesso colore.
☐ A questo punto, grazie alle due precedenti manovre, molto semplici, si trovano al posto giusto ben 24 faccette (i 2/3 del totale). Restano da sistemare solo le 12 faccette appartenenti ai 6 spigoli.
☐ La messa a punto degli spigoli comporta l’esecuzione di alcune manovre un po’ più complesse delle precedenti; per indicarle in maniera sintetica conviene adottare la seguente simbologia, relativamente ai 3 strati triangolari che convergono su una determinata faccia della piramide:
• A → lo strato superiore viene ruotato di una posizione verso sinistra;
• A′ → lo strato superiore viene ruotato di una posizione verso destra;
• S → lo strato inferiore sinistro viene ruotato di una posizione verso il basso;
• S′ → lo strato inferiore sinistro viene ruotato di una posizione verso l’alto;
• D → lo strato inferiore destro viene ruotato di una posizione verso il basso;
• D′ → lo strato inferiore destro viene ruotato di una posizione verso l’alto;
☐ Per seguitare nel procedimento risolutivo, è opportuno tenere la piramide in una determinata posizione (senza più ribaltarla in seguito) e osservare quanti spigoli bisogna spostare nello strato trapezoidale inferiore, per renderlo tutto di colore uniforme.
☐ Se un potenziale spigolo da spostare si trova nello strato triangolare superiore, si possono avere tre possibilità.
a) Lo spigolo si trova a sinistra e mostra una faccetta dello stesso colore di quello della base inferiore dello strato trapezoidale; in questo caso, la manovra da compiere è la seguente:
b) Lo spigolo si trova a destra e mostra una faccetta dello stesso colore di quello della base inferiore dello strato trapezoidale; in questo caso, la manovra da compiere è la seguente:
c) Lo spigolo non si trova in nessuna di queste due posizioni; in questo caso bisogna:
• ruotare lo strato superiore, verso destra o verso sinistra, in modo da ottenere una delle due configurazioni prima indicate;
• eseguire la manovra relativa alla situazione raggiunta;
• ruotare lo strato superiore, in modo da riportarlo nella posizione precedente.
☐ Se un potenziale spigolo da spostare si trova già nello strato trapezoidale inferiore ma in posizione ribaltata (con i due colori invertiti), bisogna portarlo nello strato triangolare superiore, eseguendo una delle due manovre precedenti, e poi procedere di conseguenza.
☐ Dopo aver completato lo strato trapezoidale inferiore, rimangono da collocare i tre spigoli del corrispondente strato triangolare; i modi in cui questi possono presentarsi sono solo quattro.
a) I tre spigoli si trovano al posto giusto, correttamente sistemati; in questo caso, il rompicapo è già risolto.
b) I tre spigoli si trovano al posto giusto, ma solo uno di loro è correttamente sistemato; in questo caso, per ribaltare gli altri due, basta effettuare la seguente manovra:
c) I tre spigoli si trovano sfalsati di una posizione in senso antiorario (non necessariamente tutti correttamente sistemati); in questo caso, per portarli negli alloggiamenti giusti, basta effettuare la seguente manovra:
d) I tre spigoli si trovano sfalsati di una posizione stavolta in senso orario (non necessariamente tutti correttamente sistemati); in questo caso, per portarli negli alloggiamenti giusti, basta effettuare la seguente manovra (speculare alla precedente):
• Se al termine di una delle due manovre precedenti (punti c o d), due spigoli risultano non correttamente sistemati, per completare la sistemazione della piramide, basta applicare la manovra descritta al punto b.
■ Nota. Il primo prototipo di questo rompicapo è stato realizzato in maniera artigianale nel 1970 dall’artista svizzero Uwe Mèffert, residente a Hong Kong; la sua commercializzazione, è avvenuta solo nel 1981. Mèffert, infatti, non pensava che la propria creazione potesse suscitare l’interesse del pubblico. Dopo l’enorme successo incontrato dal Cubo di Rubik (vedi scheda successiva), decise di proporla a un distributore giapponese e, con suo grande stupore, riuscì a venderne ben 90 milioni di pezzi in soli tre anni.
8.4 Cubo di Rubik (Ernö Rubik, 1975)
Il materiale di gioco è costituito da un cubo di plastica suddiviso in un insieme di 26 blocchetti mobili, collegati tra loro e sagomati in maniera tale che ciascuna delle 6 facce del cubo risulti scomposta in 9 quadratini uguali, colorati in 6 tinte diverse (per un totale di 6 × 9 = 54 quadratini).
Partendo da una configurazione disordinata in cui i quadrati sono disposti in maniera casuale, l’obiettivo principale consiste nel rendere ogni faccia di colore uniforme, ruotando opportunamente i vari blocchetti mobili.
■ Soluzione. La ricerca di un procedimento risolutivo per questo rompicapo è estremamente complessa, per almeno due motivi principali:
• la quantità delle potenziali configurazioni di partenza è estremamente elevata (circa 43 miliardi di miliardi), mentre è praticamente unica quella che bisogna riuscire a ottenere;
• non è facile riuscire a visualizzare, in uno spazio tridimensionale, gli effetti che possono derivare da una sequenza formata anche da poche rotazioni di insiemi di blocchetti.
Da quando il gioco è stato inventato solo pochissime persone, in tutto il mondo, sono riuscite a ricavare in maniera autonoma un algoritmo risolutivo completo. La maggior parte di coloro che sono in grado di ricomporre le facce del cubo in maniera più o meno veloce ricorre all’applicazione di uno di tali procedimenti, divulgati dagli autori.
Il metodo risolutivo proposto nel presente contesto è una rielaborazione di quello ideato nel 1980 dal matematico Stefano Pallottino (il primo italiano a riuscire nell’impresa). La sua applicazione è relativamente semplice in quanto avviene per gradi e richiede solo sette manovre principali da apprendere.
In seguito, per praticità espositiva, i potenziali colori dei vari quadratini vengono indicati mediante dei simboli geometrici. Questa scelta è motivata sia dalla difficoltà di contrastare adeguatamente, in bianco e nero, le sfumature di grigio corrispondenti ai 6 colori previsti, sia dalla constatazione che i vari cubi in commercio non sono tutti colorati nello stesso modo. È bene precisare però che tali simboli non vanno associati a dei colori prestabiliti, ma a quelli che si vedrebbero tenendo il cubo in una determinata posizione. In particolare, il simbolo del cerchietto con un puntino al centro, corrisponde sempre al colore della faccia che va tenuta in posizione frontale nel corso di una determinata manovra. Ovviamente, quando la posizione del cubo viene modificata, cambia anche la corrispondenza tra i simboli e i colori. Ogni quadratino che non può essere associato a un colore determinato, viene lasciato privo di simboli (ovvero bianco).
In merito alle potenziali posizioni che possono assumere i vari blocchetti, per sinteticità espositiva, nel seguito vengono adottate le seguenti definizioni:
• posto giusto, la posizione che un determinato blocchetto deve occupare, nel cubo risolto, indipendentemente dall’orientamento dei propri quadratini;
• collocazione corretta, la posizione che un determinato blocchetto deve occupare per trovarsi non solo al posto giusto, ma anche con tutti i quadratini orientati in base al colore delle facce di appartenenza.
Per affrontare in maniera razionale la ricerca di un procedimento risolutivo per questo rompicapo, è necessario analizzare la struttura meccanica dell’oggetto da manipolare.
Innanzitutto, si può notare che i blocchetti mobili in cui è suddiviso il cubo sono di tre tipi diversi: angoli, centri e spigoli.
In dettaglio, si contano:
• 6 centri, ognuno dei quali mostra un quadratino;
• 12 spigoli, ognuno dei quali mostra 2 quadratini;
• 8 angoli, ognuno dei quali mostra 3 quadratini.
Per quanto riguarda i potenziali movimenti effettuabili, è importante notare che i 6 centri sono imperniati su una struttura fissa e che, quindi, possono solo ruotare su sé stessi, senza spostarsi dalle rispettive posizioni.
Di conseguenza, il colore di ciascun quadratino centrale deve necessariamente coincidere con quello assunto dalla relativa faccia nel cubo ricomposto. In pratica intorno a ciascun centro devono essere sistemati i restanti quadratini dello stesso colore.
Se si osserva il modo in cui sono disposti gli altri blocchetti intorno alla struttura centrale, si può notare che ogni spigolo confina con 2 centri lungo 2 lati, mentre ogni angolo tocca 3 centri solo mediante 3 vertici.
A causa di questa particolare costruzione è evidente che, nel corso dei vari spostamenti possibili, ciascuno di tali blocchetti (spigolo o angolo) può andare a occupare solo la posizione di un analogo blocchetto.
Si può verificare che l’unico tipo di mossa effettuabile comodamente consiste nel ruotare uno strato esterno, composto da un centro, 4 spigoli e 4 angoli. In teoria, sarebbe anche possibile ruotare, in un dato verso, uno strato centrale composto da 4 centri e 4 spigoli; è preferibile, però, ottenere lo stesso risultato ruotando nel verso opposto i due strati esterni che lo racchiudono. Analogamente sarebbe possibile ruotare insieme, in un dato verso, due strati contigui (uno centrale e uno esterno); è preferibile però ottenere lo stesso risultato ruotando nel verso opposto l’altro strato esterno, a essi parallelo.
In seguito, per indicare in maniera sintetica le singole mosse richieste dal procedimento risolutivo, viene adotatta la seguente simbologia, riferita ai cinque strati esterni che convergono su una stessa faccia frontale (non viene preso in considerazione solo lo strato posteriore, non visibile a chi manipola il cubo):
• A → lo strato superiore viene ruotato di una posizione verso sinistra;
• A′ → lo strato superiore viene ruotato di una posizione verso destra;
• B → lo strato inferiore viene ruotato di una posizione verso sinistra;
• B′ → lo strato inferiore viene ruotato di una posizione verso destra;
• D → lo strato destro viene ruotato di una posizione verso il basso;
• D′ → lo strato destro viene ruotato di una posizione verso l’alto;
• S → lo strato sinistro viene ruotato di una posizione verso il basso;
• S′ → lo strato sinistro viene ruotato di una posizione verso l’alto;
• F → lo strato frontale viene ruotato di una posizione verso sinistra;
• F′ → lo strato frontale viene ruotato di una posizione verso destra;
Durante l’esecuzione di una manovra, è importante mantenere il cubo sempre nella stessa posizione in modo da poter individuare con coerenza gli strati che devono essere ruotati.
Solo prima di passare a eseguire un’altra sequenza di mosse, se necessario, si può far ruotare il cubo intorno all’asse verticale (per scegliere la faccia frontale più opportuna).
I tre strati orizzontali in cui può essere suddiviso il cubo vengono abitualmente denominati nel seguente modo.
Il procedimento illustrato nel presente contesto, è suddiviso in queste tre fasi:
• sistemazione del primo strato, in modo che la sua faccia assuma lo stesso colore del relativo centro e che ognuno dei suoi 4 bordi mostri lo stesso colore del corrispondente centro sottostante;
• sistemazione del secondo strato, in modo che ognuno dei suoi 4 bordi mostri lo stesso colore del relativo centro;
• sistemazione del terzo e ultimo strato, in modo che ciascuna delle 6 facce del cubo assuma lo stesso colore del proprio centro.
☐ Primo strato
La messa a punto del primo strato non crea grandi difficoltà, potendo essere effettuata senza la preoccupazione di mantenere l’assetto degli altri due strati (ancora da sistemare).
• Per compiere questa operazione nel modo più rapido, conviene collocare prima i 4 spigoli e poi i 4 angoli. Infatti, non sempre è possibile incastrare uno spigolo tra due angoli, senza spostarne almeno uno, mentre è più agevole inserire un angolo tra due spigoli, mantenendo le loro posizioni.
• Prima di iniziare, per tentare di risparmiare qualche mossa, è consigliabile controllare se, casualmente, in qualcuno dei 6 strati esterni del cubo vi siano già alcuni spigoli sistemati correttamente (o che possano esserlo mediante una semplice rotazione). In tal caso, conviene fissare come primo strato quello che ne contiene il numero maggiore.
• Siccome in questa fase iniziale la composizione del cubo è ancora disordinata, esistono vari potenziali casi da esaminare in merito alla sistemazione degli spigoli. Non è però indispensabile analizzarli tutti in dettaglio, essendo in buona parte risolvibili in maniera intuitiva mediante l’effettuazione di poche mosse elementari.
• L’unica situazione relativamente meno immediata si presenta quando uno spigolo si trova (o può essere facilmente portato) nel terzo strato, sotto un centro che non può scavalcare e che gli impedisce di raggiungere direttamente la propria collocazione corretta. In questo caso, la manovra da compiere per ottenere tale risultato, senza spostare eventuali spigoli già sistemati, è la seguente.
• Questa stessa successione di mosse può tornare utile anche per modificare adeguatamente la posizione di uno spigolo collocato in uno dei 3 strati orizzontali, in maniera non funzionale.
• Una volta sistemati correttamente i 4 spigoli del primo strato, il cubo viene ad assumere un aspetto analogo al seguente.
• Per completare la costruzione del primo strato, quindi, bisogna riuscire a sistemare correttamente anche i 4 angoli. I casi da analizzare al riguardo non sono molti perché, per la struttura del cubo, questi possono trovarsi solo o nel primo o nel terzo strato.
• Se un angolo si trova (o può essere facilmente portato) nel terzo strato, in posizione tale da poter raggiungere la propria collocazione corretta mediante una semplice rotazione antioraria dello strato laterale sinistro, la manovra da effettuare per ottenere tale risultato (senza spostare i blocchetti già sistemati) è la seguente.
• Analogamente, se un angolo si trova (o può essere facilmente portato) nel terzo strato, in posizione tale da poter raggiungere la propria collocazione corretta mediante una semplice rotazione oraria dello strato laterale destro, la manovra da effettuare per ottenere tale risultato (senza spostare i blocchetti già sistemati) è la seguente (speculare della precedente).
• Queste stesse due successioni di mosse possono tornare utili anche per rimuovere dal primo strato un angolo collocato in maniera non corretta o per orientare in maniera conveniente un angolo posto nel terzo strato.
Il completamento del primo strato, quindi, può essere attuato effettuando solo le due manovre precedenti, eventualmente più volte di seguito.
Una volta messo a posto il primo strato, il cubo viene ad assumere un aspetto analogo al seguente.
☐ Secondo strato
La messa a punto del secondo strato è meno semplice della precedente, dovendo essere effettuata senza alterare l’assetto del primo strato appena sistemato. I casi da prendere in considerazione non sono comunque molti, perché riguardano solo le possibili dislocazioni di 4 spigoli (i 4 centri, infatti, si trovano già al posto giusto, per costruzione).
• Se uno spigolo si trova (o può essere facilmente portato) nel terzo strato, in posizione tale da poter raggiungere la propria collocazione corretta mediante una semplice rotazione antioraria dello strato frontale, la manovra da effettuare per ottenere tale risultato e senza spostare i blocchetti già sistemati è la seguente.
• Similmente, se uno spigolo si trova (o può essere facilmente portato) nel terzo strato, in posizione tale da poter raggiungere la propria collocazione corretta mediante una semplice rotazione antioraria dello strato frontale, la manovra da effettuare per ottenere tale risultato, senza spostare i blocchetti già sistemati, è la seguente (speculare della precedente).
• Queste stesse due successioni di mosse possono tornare utili per rimuovere dal secondo strato uno spigolo posizionato a colori invertiti.
La sistemazione del secondo strato, quindi, può essere attuata effettuando solo le due manovre precedenti, eventualmente più volte di seguito.
Una volta messo a posto anche il secondo strato il cubo viene ad assumere un aspetto analogo al seguente.
☐ Terzo strato
La messa a punto del terzo strato è indubbiamente la più complessa, dovendo essere effettuata senza alterare l’assetto del primo e del secondo strato (già sistemati). Inoltre i casi da prendere in considerazione non sono pochi perché riguardano le possibili dislocazioni di 4 spigoli e di 4 angoli.
A tale scopo è opportuno ricorrere a delle successioni di mosse che agiscano su più blocchetti contemporaneamente, non essendo conveniente spostarli uno alla volta. Considerati i particolari effetti di tali manovre, risulta più vantaggioso sistemare prima gli angoli e poi gli spigoli.
Alla luce di tali considerazioni, la successione delle operazioni da compiere per sistemare il terzo strato può essere esposta nel modo seguente.
1. Collocazione degli angoli al posto giusto
Per compiere rapidamente questa prima operazione, bisogna ruotare il terzo strato cercando di individuare la posizione che presenta il maggior numero di angoli al posto giusto. Matematicamente tale valore può essere uguale solo a 2 o 4.
• Nel caso fortunato in cui si riescono a portare tutti e 4 gli angoli al posto giusto, la situazione è già risolta e si passa direttamente all’operazione successiva.
• Se gli angoli al posto giusto sono 2 e si trovano affiancati (ovvero se appartengono a uno stesso strato verticale), è possibile scambiare di posto gli altri 2 angoli, effettuando la seguente manovra (dopo avere posto come faccia frontale quella in cui si trovano i 2 angoli al posto giusto).
• Se i 2 angoli al posto giusto non sono affiancati (ovvero se si trovano su due vertici opposti del terzo strato), si può effettuare una sola volta la manovra precedente per scambiare la posizione di due angoli qualsiasi e riportarsi così al caso prima analizzato.
2. Corretto orientamento degli angoli
Per poter compiere rapidamente questa seconda operazione è necessario controllare quanti degli angoli, messi prima al posto giusto, sono anche già correttamente sistemati. Matematicamente, possono essere: 0, 1, 2 o 4.
• Nel caso fortunato in cui tutti e 4 gli angoli si trovano in questo stato, la situazione è già risolta e si passa direttamente all’operazione successiva.
• Se un solo angolo è già correttamente sistemato, bisogna posizionare il cubo frontalmente in modo che questo particolare angolo sia affiancato nell’angolo opposto da un quadratino del colore della faccia inferiore.
• Partendo da una configurazione del genere, se l’angolo già orientato si trova sulla sinistra, è possibile sistemare gli altri tre, con una sola esecuzione della seguente manovra.
• Analogamente, se l’angolo già orientato si trova sulla destra, è possibile sistemare gli altri tre con una sola esecuzione di quest’altra manovra (speculare della precedente).
• Se (contrariamente a quanto prima ipotizzato) la situazione iniziale dovesse mostrare 0 o 2 angoli già correttamente sistemati, ci si può ricondurre a quella prima analizzata (nella quale un solo angolo è in tale condizione), effettuando opportunamente le due manovre precedenti.
• Per evitare di dover compiere più volte e più volte tali successioni di mosse prima di riuscire a ottenere la configurazione desiderata, è necessario posizionare il cubo in base ai seguenti accorgimenti:
a) se nessun angolo è già correttamente orientato, bisogna scegliere come faccia frontale quella che non mostra, negli angoli, due quadratini dello stesso colore della faccia inferiore;
b) se ci sono 2 angoli già correttamente orientati, bisogna scegliere come faccia frontale quella che mostra, nell’angolo sinistro, un quadratino dello stesso colore di quello della faccia inferiore.
• Rispettando tali indicazioni, è sufficiente eseguire una sola volta la seconda delle due manovre precedentemente illustrate, per riportarsi al caso in cui uno solo dei quattro angoli è già correttamente orientato.
3. Corretto orientamento degli spigoli
Per poter compiere rapidamente questa terza operazione è necessario controllare quanti spigoli del terzo strato mostrano, nella faccia inferiore, dei quadratini dello stesso colore di quello centrale (ma non necessariamente già correttamente orientati). Matematicamente possono essere: 0, 2 o 4.
• Nel caso fortunato in cui tutti e 4 gli spigoli si trovano in tale stato, la situazione è già risolta e si passa direttamente all’operazione successiva.
• Se, nella faccia inferiore ci sono 2 quadratini di colore diverso da quello centrale e confinano per un vertice, bisogna posizionare il cubo in modo che questa coppia di quadratini sia collocata in fondo a destra.
• Partendo da una configurazione del genere, è possibile fare in modo che tutti i quadratini della faccia inferiore mostrino lo stesso colore, con una sola esecuzione della manovra qui di seguito illustrata.
• Nel caso in cui nessuno spigolo dovesse mostrare, nella faccia inferiore, un quadratino dello stesso colore di quello centrale, effettuando la manovra precedente è possibile ricondursi alla situazione prima analizzata (nella quale due spigoli sono in tale condizione).
• Se, invece, nella faccia inferiore ci sono quadratini di colore diverso da quello centrale che però non confinano per un vertice, non è possibile ricondursi alla situazione prima analizzata effettuando la manovra precedente. Questa, infatti, non si limita a ribaltare gli spigoli, ma modifica anche la loro posizione. Quindi se viene eseguita a partire dalla configurazione in oggetto finisce per riproporne una analoga.
• Per aggirare l’ostacolo, bisogna posizionare il cubo in modo che i due quadratini anomali si trovino alle estremità dello strato centrale verticale e, dopo, compiere la manovra qui di seguito indicata.
4. Corretta sistemazione degli spigoli (e completamento del cubo)
Per poter compiere rapidamente quest’ultima operazione, è necessario controllare quanti spigoli del terzo strato sono già correttamente sistemati. Matematicamente, possono essere: 0, 1 o 4.
• Nel caso fortunato in cui tutti e 4 gli spigoli sono correttamente sistemati, la situazione è già risolta e il riordino del cubo è terminato.
• Se c’è un solo spigolo correttamente sistemato, bisogna orientare il cubo in modo che questo spigolo si trovi nello strato posteriore. Poi, tenendo il cubo in tale posizione, bisogna osservare dove si trova il quadratino che ha lo stesso colore della faccia frontale.
• Se quel quadratino si trova alla sinistra della faccia frontale, è possibile sistemare correttamente tutti i 4 spigoli del terzo strato, con una sola esecuzione della seguente manovra.
Analogamente, se quel quadratino si trova alla destra della faccia frontale, è possibile sistemare correttamente tutti i 4 spigoli del terzo strato, con una sola esecuzione della seguente manovra (speculare della precedente).
• Se, contrariamente a quanto prima ipotizzato, la situazione iniziale non dovesse mostrare alcuno spigolo già correttamente sistemato effettuando una delle due manovre precedenti, ci si può ricondurre a una delle due situazioni prima analizzate (nelle quali uno spigolo è in tale condizione).
■ Nota. Il geniale meccanismo su cui si basa questo rompicapo è stato inventato nel 1974 dal professore di architettura e scultore ungherese Ernő Rubik, nell’intento di realizzare una particolare giuntura per la costruzione di mobili. Il prototipo messo a punto in quell’occasione era di legno, aveva gli angoli smussati e ogni faccia mostrava lo stesso colore. All’inizio del 1975, dopo aver apportato alla propria creazione le sostanziali modifiche che permangono nel modello attuale, Rubik la brevettò, denominandola Magic Cube.
Nel Natale del 1977 la fabbrica ungherese Politechnika mise in vendita, in un grande magazzino di Budapest, i primi 5000 pezzi del rompicapo, che vennero venduti tutti in pochissimi giorni. Qualche settimana dopo in quella stessa città venne fondato un Club del Cubo, la cui prima riunione vide la partecipazione di circa duemila persone.
Nell’estate del 1978 il gioco venne presentato dal matematico ungherese Tamas Varga, amico di Rubik, al Congresso internazionale di matematica che si teneva ad Helsinki in Finlandia. David Singmaster, professore di teoria dei gruppi presso il Polytechnic of South Bank di Londra, ne rimase affascinato e prese l’iniziativa di diffonderlo, curandone anche il lancio commerciale su vasta scala. Poco dopo, l’azienda statunitense Ideal Toy ribattezzò il rompicapo Rubik’s Cube (cubo di Rubik) e cominciò a produrlo a ritmo sostenuto nei propri stabilimenti negli Stati Uniti, a Hong Kong e nelle Antille, inondando il mercato mondiale già alla fine del 1978. Attualmente, il Cubo di Rubik risulta essere il gioco più diffuso di tutti i tempi, con circa 300 milioni di esemplari venduti (considerando anche le versioni non ufficiali).
È da sottolineare che lo straordinario successo di questo rompicapo ha avuto un provvidenziale effetto per il settore dei giochi matematici. Infatti ha favorito il sorgere, in tutto il mondo, di un grande fermento di attività ludiche legate alla matematica (cura di rubriche specialistiche, pubblicazione di libri e riviste, costituzione di associazioni e federazioni, organizzazione di campionati e convegni e così via), molte delle quali ancora attive, a distanza di più di trent’anni.
8.5 Genius (Anonimo, 1981)
Il materiale di gioco consiste in un cilindro di plastica, suddiviso in 3 parti ruotanti attorno a uno stesso asse; su ognuna di queste parti è avvolto ad anello uno strato di 6 caselle. La superficie laterale del cilindro risulta ripartita in 6 settori paralleli non comunicanti direttamente tra loro, ognuno dei quali contiene 3 caselle. Su tale superficie sono inserite 17 tessere di 6 colori differenti (5 colori sono presenti su 3 tessere ciascuno, mentre un colore è presente solo su 2 tessere). Una casella è lasciata vuota, per consentire gli spostamenti delle tessere.
Quando una tessera si trova in una posizione adiacente a quella della casella vuota, può essere spostata orizzontalmente (a destra o a sinistra), andando a occuparne lo spazio.
Partendo da una configurazione disordinata e casuale, l’obiettivo principale consiste nel rendere di colore uniforme ognuno dei 6 settori, ruotando le parti mobili del cilindro e spostando le tessere nella maniera più funzionale.
■ Soluzione. La soluzione di questo rompicapo è piuttosto semplice, sia perché il numero di disposizioni ottenibili non è molto elevato, sia perché esistono diverse classi di configurazioni equivalenti. L’assegnazione dei colori ai vari settori, infatti, non è prestabilita; inoltre le tessere di uno stesso colore sono interscambiabili, non essendo vincolate ad appartenere a determinate posizioni.
L’unico problema da affrontare consiste nel riuscire a trovare il modo di trasferire una qualsiasi tessera in un particolare punto del cilindro (senza guastare la situazione già impostata), tenendo conto dei vincoli di movimento imposti dalla struttura dell’oggetto da manipolare.
Qui di seguito viene descritta una manovra molto semplice che consente di scambiare la posizione della casella vuota con quella di una determinata tessera lasciando immutata la disposizione delle altre 16 tessere. Per risolvere completamente il gioco, basta quindi applicare più volte questa unica manovra, adattandola opportunamente alle circostanze.
• All’inizio, la tessera da spostare e la casella vuota da riempire devono trovarsi su due strati contigui.
Per ottenere una condizione del genere (se non è già in atto), basta trasferire nella casella vuota una delle 2 tessere che si trova nello stesso suo settore.
• Si ruota lo strato contenente la tessera della quantità di caselle necessaria per portarla accanto a quella vuota.
• Si inserisce la tessera nella casella vuota.
• Si riposiziona lo strato ruotandolo all’indietro della stessa quantità di caselle di cui era stato spostato.
• Se la casella che una determinata tessera dovrebbe raggiungere si trova in uno dei settori senza casella vuota, bisogna applicare due volte la manovra precedente: una volta per liberare la casella di arrivo desiderata (trasferendo nella casella vuota la tessera che la occupa); un’altra per inserirvi la tessera presa in considerazione.
■ Nota. Non è noto l’inventore di questo gioco, ma è certo che è stato realizzato nel 1981 con il nome di Whip-it da una ditta di Taiwan e commercializzato da un grande distributore statunitense. Fra tutti i rompicapi tridimensionali che hanno invaso il mercato, dopo il grande successo del Cubo di Rubik, questo è indubbiamente il più semplice. Tra l’altro, può essere definito tridimensionale solo per la propria forma: in realtà consiste in una sorta di Gioco del 15 arrotolato su un cilindro. Nonostante tali caratteristiche poco stimolanti, il gioco ha avuto una larga diffusione a livello mondiale anche perché in vari paesi (tra cui l’Italia) è stato messo in vendita in una speciale confezione contenente anche il Cubo di Rubik. La sua semplicità di risoluzione lo rende decisamente più rilassante di tutti gli altri rompicapi della stessa categoria.