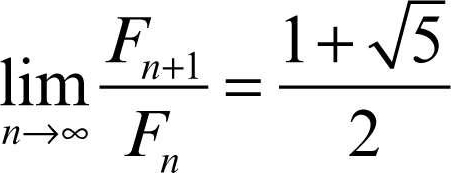Girard

Girard

Girard Albert (Saint-Mihiel, Lorena, 1595 - L’Aia 1632) matematico francese. È noto per i suoi lavori in algebra, aritmetica e trigonometria, nell’ambito della quale gli si deve il teorema sui triangoli sferici che porta il suo nome (→ triangolo sferico). Membro della chiesa riformata, si stabilì in Olanda, dove studiò matematica all’università di Leida, iscrivendosi tuttavia soltanto all’età di 22 anni, essendo il suo interesse prevalente la musica: suonava, infatti, il liuto a livello professionistico. Nel 1625 preparò una versione critica della Arithmétique di S. Stevin cui aggiunse una traduzione dal greco dei libri 5 e 6 della Aritmetica di Diofanto di Alessandria. L’anno successivo, nel volume Trigonométrie, utilizzò per primo le notazioni sin, cos, tan per le funzioni goniometriche e ne fornì delle tavole di valori che miglioravano quelli proposti dallo stesso Stevin. Nel testo Invention nouvelle en algèbre (Nuova invenzione in algebra, 1629) presentò quello che sarà poi conosciuto come triangolo di Tartaglia o di Pascal (→ Tartaglia, triangolo di), da lui chiamato triangolo di estrazione, ed enunciò, senza dimostrarlo, il cosiddetto teorema fondamentale dell’algebra (un’equazione algebrica di grado n ha esattamente n radici nel campo complesso). A Girard si devono anche la prima formulazione della definizione ricorsiva della successione di Fibonacci, F_n+2 = F_n+1 + F_n, a partire dai dati iniziali F₀ = 0, F₁ = 1, e l’affermazione che il rapporto tra due successivi numeri di Fibonacci tende al → numero aureo:

Girard intravide, prima di Cartesio, la regola dei segni per le equazioni di secondo grado e fu il primo a esprimere la somma delle potenze di uguale esponente delle radici di una equazione algebrica (fino al quarto grado) in funzione dei coefficienti.