Gli strumenti dello scambio: i sistemi di misura
Gli strumenti dello scambio: i sistemi di misura
Vicino oriente ed egitto
i sistemi di misura lineari, ponderali e di capacità vicino-orientali
di Maria Giovanna Biga
Le unità di misura (di lunghezza, di peso e di capacità) nel Vicino Oriente antico sono variate a seconda dei luoghi e dei periodi. È possibile però riconoscere dei sistemi standardizzati di misura dal momento che furono sovente utilizzati come unità di misura degli elementi "naturali", di dimensioni quindi pressappoco uguali dovunque. La conversione delle antiche unità di misura con le corrispondenti nostre misure può essere solo approssimativa.
Misure di lunghezza
Le misure di lunghezza in tutto il Vicino Oriente antico furono abbastanza standardizzate perché si basavano su unità di misura tratte dalla natura e il loro uso era semplice (Tab. 1). La più piccola unità di misura di lunghezza (utilizzata anche come unità di peso e base per tutte le altre misure di lunghezza e di superficie e di volume da esse derivate) era il grano d'orzo (sumerico: š e ; accadico: uṭṭetu). Suoi principali multipli erano: il dito (considerato equivalente a 6 grani d'orzo); il palmo (della mano, cioè una mano chiusa); la spanna (distanza tra il pollice e l'indice a mano aperta); il cubito (l'avambraccio, la distanza tra il gomito e la punta delle dita); la canna (strumento di misura oltreché misura equivalente a 6 cubiti, cioè 3 m ca.). Il cubito standard mesopotamico era di 50 cm circa ed era la misura più usata; si misurava in cubiti l'altezza di una persona, ci si basava su di esso per determinare le dimensioni di un edificio. Una rappresentazione del cubito sumerico è pervenuta da una statua di Gudea, sovrano della città di Lagash (databile al 2100 a.C. ca.), conservata al Louvre e detta "l'architetto con pianta", perché il sovrano è seduto e sul grembo ha la pianta di un edificio misurata in cubiti. Il cubito ebraico misurava 44,45 cm circa. Veniva utilizzato però anche un cubito ''reale", più lungo del cubito standard, corrispondente al cubito mesopotamico e approssimativamente equivalente anche al cubito egiziano. Misure più lunghe del cubito e della canna servivano a misurare i campi e le distanze tra due luoghi. Tali misure sono tutte multipli del cubito e della canna. Tra le principali si annoverano: la pertica -nindan (6 m ca., cioè 2 canne = 12 cubiti); la fune (o fune mensoria, usata per misurare i campi, lunga 60 m ca., cioè 10 pertiche-nindan = 20 canne = 120 cubiti); la misura bēru con cui si indicava una ''tappa'', chiamata anche ''doppia ora'', 10,8 km circa, quanto cioè si calcolava si percorresse in due ore di marcia. Queste misure di lunghezza ''naturali'' erano abbastanza standardizzate e sono state utilizzate in tutto il Vicino Oriente antico (con piccole oscillazioni di valori a seconda dei luoghi e dei periodi) a partire dal periodo sumerico. Nei testi matematici paleobabilonesi le unità di lunghezza sono normalmente espresse come frazioni sessagesimali o multipli della pertica-nindan.
Misure di superficie
Le unità di misura di superficie e la geometria piana mesopotamica furono determinate da problemi pratici, come la necessità di misurare i campi e le esigenze dell'amministrazione. In Mesopotamia le parcelle di terra coltivabili dovevano essere misurate con la più grande esattezza per poter calcolare esattamente la quantità di semenza necessaria e per poter anche calcolare preventivamente il rendimento dei campi. Esistevano campi e parti di campi rettangolari e in triangolari, ma anche in forma di poligoni irregolari. Per poterne calcolare l'area i Mesopotamici li divisero in triangoli e in rettangoli, dopo che ne erano stati misurati i confini. La somma delle aree di queste figure semplici forniva l'area totale. Una tavoletta paleobabilonese ad esempio descrive un campo diviso in quattro triangoli, tre trapezoidi e sette triangoli regolari. Si utilizzò come base di computo la misura di lunghezza della pertica-nindan, fissando una stabile connessione tra il quadrato di tale pertica e il sistema per calcolare l'area. La pertica- nindan fu infatti definita già in periodo sumerico come il lato di un š a r (piccolo appezzamento di terreno) e quindi costituì l'unità di base di calcolo non solo nei sistemi di lunghezza, ma anche nei sistemi da questi derivati e con questi messi in relazione, di area e di volume. Le misure di lunghezza poi furono poste anche in relazione con quelle di capacità e di peso. Tale sistema di misurazione fu adottato nei testi matematici e costituì dunque il fondamento per la geometria scientifica; è documentato fino al periodo seleucide anche nei calcoli delle distanze celesti. Dal periodo cassita al periodo neobabilonese la superficie di un terreno venne calcolata in unità di capacità, cioè con la quantità di orzo necessaria per seminarlo. Si calcolava che un b u r di terra richiedeva 240 s ì l a di semenza. Sono comunque documentati anche altri modi di misurare le superfici in Mesopotamia settentrionale e in Siria. Nella Bibbia non vi sono termini per le misure di superficie; questa era determinata con l'indicazione della lunghezza dei lati di un rettangolo o di un quadrato. I terreni erano misurati con misure ricavate empiricamente; lo iugero (letteralmente giogo, coppia) era l'estensione di terreno che una coppia di buoi poteva arare in un giorno. Inoltre, come in Mesopotamia, si calcolava anche la superficie di un terreno in base alla quantità d'orzo necessaria per seminarlo. In Mesopotamia nel III e nel II millennio, fino al periodo paleobabilonese, si utilizzò come unità base di misure di superficie lo š a r, che equivaleva ad un quadrato di una pertica- nindan di lato. Molto usata era la misura i k u, ''diga di terra'', che equivaleva a 100 š a r, cioè 0,36 ha circa. Il multiplo più grande era il b u r, cioè un lungo rettangolo avente come base una pertica-nindan (6 m ca.) e un lato di 1 bēru (10,8 km ca.). La misura base i k u aveva una serie di sottomultipli, frazioni equivalenti a 1/8, 1/4, 1/2 di i k u.
Misure di volume
Anche le misure di volume utilizzate nel Vicino Oriente antico erano derivate da necessità pratiche, ad esempio per stimare quanta terra era stata scavata per un canale, quanti mattoni sarebbero stati necessari (e quindi quanti lavoratori servivano e per quanto tempo) per costruire un tempio, ecc. Il sistema standard di misure di volume fu canonizzato nei testi matematici paleobabilonesi. Le unità di volume erano definite come solidi rettangolari aventi la base di una unità di superficie e l'altezza/profondità di 1 cubito. Il sistema è basato su questa equivalenza: 1 š a r di area per 1 cubito di altezza/profondità = 1 š a r di volume = 60 sicli di volume = 60 g u r (= 18.000 s ì l a ) di capacità.
Unità di misura ponderali
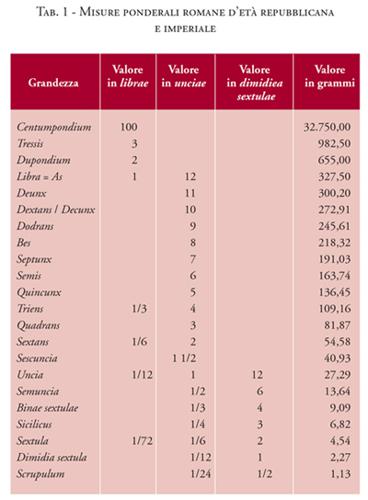
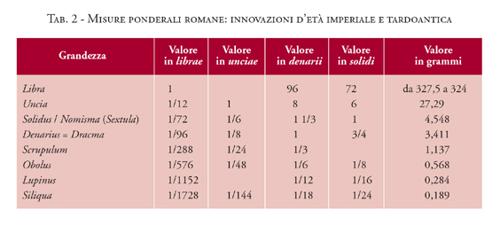
In tutto il Vicino Oriente antico si utilizzavano come pesi le pietre semplicemente appiattite da un lato oppure modellate ad esempio in forma ellissoidale con le estremità appiattite, oppure in forma di animale (pesci, anatre, leoni e bovidi vari, stambecchi, gazzelle, falchi, ippopotami, topi, rane) o di figura umana. Sovente un'iscrizione indicava il peso e l'unità di misura rappresentata. I musei conservano molti di questi pesi. Sono conosciuti parecchi sistemi ponderali diversi nel Vicino Oriente antico a seconda dei luoghi e del periodo. Comuni a tutti i periodi sono: lo š e, il grano di orzo, la più piccola unità di misura di peso corrispondente a 0,04629 g; il suo multiplo, il siclo (g ín / šiklu) = 8,333 g; la mina (ma - na /manû) = 60 sicli = 50 g; il talento (g ú/biltu) = 60 mine = 30 kg (Tab. 2). Naturalmente nei diversi periodi e nei diversi paesi si usarono sicli e quindi mine e talenti di pesi variati, maggiori o minori. La frazione più piccola del siclo (= 1/24 di siclo) era l'obolo. Dalla Bibbia è evidente che si utilizzavano le stesse unità di misura di peso; in 2 Re, 18,14 si ricordano i 30 talenti d'oro pagati dal re Ezechia in tributo al re assiro Sennacherib, che nei suoi Annali ricorda di aver ricevuto esattamente questa somma. In parecchi scavi del Vicino Oriente (Mesopotamia, Siria, Cipro) sono stati rinvenuti dei pesi. Erano degli oggetti comunque preziosi, che appartenevano solo al re e ai grandi commercianti. Dai testi in cuneiforme è evidente che erano già considerati, come i sigilli, degli oggetti di valore. Sono generalmente in pietra dura e di fattura molto curata. Ad esempio, nel Palazzo Reale Q di Ebla del periodo paleosiriano (1800- 1600 a.C. ca., Bronzo Medio) sono stati ritrovati pesi, tra cui uno, in ematite, a forma di leone. Il leone pesa 913 g; considerando che la mina siriana, già documentata ad Ebla nel III millennio a.C., aveva un valore standard di 470 g, il peso del leone corrisponde a una doppia mina siriana. La mina siriana era intermedia tra la mina babilonese di 491/505 g e quella egiziana di 437 g. La tipologia di pesi a forma leonina documentata già ad Ebla paleosiriana si affermerà poi ad Ugarit tra il XIV e il XIII sec. a.C., in Egitto nel Nuovo Regno (dalla XVIII Dinastia) e in Assiria nel I millennio a.C. Nella città di Ugarit, un regno della costa siriana fiorente tra XIV e XIII sec. a.C., sono stati rinvenuti molti pesi di diverse forme e materiali (pietre varie, tra cui ematite, bronzo, piombo, oppure di bronzo, cavi, e riempiti in piombo) i quali servivano ai mercanti di questa città che fu un grande centro di commercio e crocevia tra l'Egitto, il regno hittita, la Siria e la Mesopotamia. Dal momento che lo sviluppo e l'estensione dei commerci di Ugarit furono grandissimi, in questa città sono stati rinvenuti pesi sia delle unità ponderali locali (1 mina divisa in 50 sicli; il siclo è di 9,4 g), sia dei sistemi ponderali mesopotamici, egiziani e hittiti. Sono state pure ritrovate, più frequentemente in tombe, sia nel mondo egeo (dal periodo elladico in poi) sia nel Vicino Oriente, databili a partire dal periodo del Bronzo Recente, delle bilance. Normalmente negli scavi si rinvengono piatti rotondi fatti di una placca di bronzo circolare con i bordi rialzati che facevano parte di tali piccole bilance, usate in Siria- Palestina soprattutto dai mercanti di porpora e dagli orefici. Non dovevano servire per pesare oggetti molto pesanti; ne sono state scoperte alcune con giochi di pesi diversi e grani d'argento d'una frazione di grammo che permettevano il peso di oggetti molto delicati. Sull'Obelisco nero del re assiro Assurnasirpal II (887-853 a.C.) sono raffigurati gli Assiri che pesano le merci offerte come tributo su una bilancia a due piatti. La bilancia, di metallo, era comunque un oggetto importante e prezioso. È stata sempre preoccupazione dei vari sovrani di unificare i sistemi di e far adottare in tutto il territorio da loro dominato le stesse unità. Così già il re Ur-Nammu, il fondatore della III Dinastia di Ur (2100- 2000 a.C. ca.), che resse per un secolo tutta la Mesopotamia, in un codice di leggi da lui promulgato afferma: ''Io stabilii un recipiente 'b a r i g a ' di rame e lo standardizzai come 60 s ì l a (60 l ca.). Io fabbricai una misura 'b an' di rame e la standardizzai come 10 s ì l a (10 l ca.) di capacità. Io fabbricai una misura regale 'b an' di valore corrente (fatta) di rame e la standardizzai come misura di capacità di 5 s ì l a (5 l ca.) ... Io standardizzai le pietre-pesi dal peso di un siclo fino al peso di una mina''. Di suo figlio Shulgi si conservano in vari musei, tra cui il British Museum e il Louvre, pesi di forme diverse recanti l'iscrizione cuneiforme con indicato il valore ponderale rappresentato: sono per lo più dedicati al dio Nanna, il dio lunare venerato a Ur; verosimilmente tali pesi erano conservati nel tempio di tale dio. È ben probabile che questi pesi standard fossero conservati nei templi a garantire valore universale per quel periodo e sotto quel sovrano ad uno specifico sistema di misura e che quindi corrispondessero ai pesi di materiale meno pregiato che venivano usati comunemente dai mercanti. Così in un inno alla divinità solare Samash, il dio che tutto vede dal cielo e che è il dio della prosperità e della giustizia, si dice: ''Chi manomette le bilance, commette frode, chi sostituisce le pietre della borsa ... L'onesto nell'uso delle bilance ... di tutto gli si dona in copia ... Chi manomette la misura commette frode ... Chi impresta con la misura media, ma si fa restituire secondo la grande, in giorno non di suo destino la maledizione della gente lo coglie". Sono chiari gli intenti di eliminare le frodi, le falsificazioni delle unità di misura. Così nella Bibbia i profeti criticano i mercanti perché imbrogliano appesantendo o alleggerendo i pesi o usando pesi e bilance falsi. Già durante il III millennio a.C., quando la quantità di rame e argento aumentò grazie al commercio, questi metalli divennero unità di misura; gli scambi si effettuavano barattando il bene con una quantità di argento. Di ogni bene si calcolava il valore in argento. Perciò pezzi di argento pesati servivano come mezzo di pagamento. Il verbo per pesare (sumerico l á, accadico šaqalu) divenne il verbo usuale per ''pagare".
Misure di capacità per aridi e liquidi
Le unità di misura di capacità prendono il nome dai recipienti usati fin dai tempi più antichi per contenere aridi e liquidi, recipienti che fungevano anche da misura (Tab. 3). Sono documentati parecchi distinti sistemi di unità di misura di capacità nei vari periodi e luoghi. Il valore dell'unità di base, il g u r / kurru, è variato nei diversi periodi; sono noti g u r che oscillano da 120 a 360 s ì l a. Ad esempio nel periodo presargonico (2450-2350 a.C.) il g u r aveva una capacità di 240 s ì l a, corrispondente cioè a circa 240 l. Dal periodo di Akkad fino al periodo paleobabilonese (2350-1600 a.C. circa) venne utilizzato un gur della capacità di 300 s ì l a = 300 l circa, mentre nel periodo neobabilonese (VI sec. a.C.) un gur aveva la capacità di 180 s ì l a = 180 l circa. Sono stati utilizzati anche sistemi diversi. Ad esempio il sistema paleoassiro (2000-1800 a.C.) aveva come unità di misura base il ''sacco'' (naruqqu) che equivaleva a 4 vasi (karpatu); il vaso standard conteneva 30 s ì l a /qû. I sistemi più usati nel Nord della Mesopotamia dal II millennio a.C. in poi furono i sistemi iméru (etimologicamente: carico, soma di un asino); la misura base era quanto poteva trasportare un asino carico. Tale misura, in ebraico ḥomer, letteralmente ''soma d'asino'', era anche utilizzata in Israele come unità di misura per gli aridi.
Bibliografia
Per la traduzione dell'inno a Shamash:
G.R. Castellino, Testi sumerici e accadici, Torino 1977, pp. 383-91.
Per il codice di Ur-Nammu:
D. Frayne, Ur III Period, Toronto 1997, pp. 43-49; C. Saporetti, Antiche leggi, Milano 1998, pp. 115-21.
Per i pesi di Shulgi:
D. Frayne, Ur III Period, Toronto 1997, pp. 153-55.
Sulle unità di misura del Vicino Oriente:
M.A. Powell, s.v. Masse und Gewichte, in RlA, VII, pp. 457-517; Th. P.J. van den Hout, s.v. Masse und Gewichte. Bei den Hethitern, ibid., pp. 517-30.
La metrologia egizia
La metrologia dell'antico Egitto non presenta la stessa unitarietà di composizione di quella mesopotamica, né altrettanto consistenti sono le informazioni su cui ci si può basare, particolarmente per la definizione di valori assoluti. È possibile peraltro delineare alcune linee fondamentali di orientamento riguardo ai sistemi metrologici. L'unità di lunghezza è il cubito (meh). L'antico segno geroglifico egizio per il cubito era un avambraccio e su diverse aste cubitali egizie di pietra o legno appaiono le suddivisioni in dita, palmi, spanne grandi e piccole e piedi. Il cubito regio egizio era suddiviso in 7 palmi e 28 dita, forse in connessione con i 28 giorni del mese lunare con cui si calcolava il trascorrere del tempo, con l'ovvio rapporto di suddivisione di quattro dita per un palmo. Il cubito egizio rappresenta un elemento fondante nei sistemi generali di misura mediterranei; il cubito corto (o piccolo) egizio di 6 palmi e 24 dita fu anche il primo cubito ebraico. Il piede comune greco, che è attestato con minime varianti di lunghezza ad Atene come a Egina e in Etruria, sembra essere correlato al cubito regio di 52,3 cm nella proporzione di 3/5; la diffusione e la sopravvivenza di tale rapporto saranno avvertibili ancora nell'Inghilterra medievale nel piede di 31,7 cm in uso fino al XII secolo e negli Stati germanici medievali con l'unità rappresentata dal piede renano di 31,4 cm, forse mediante il tramite del piede romano, anch'esso derivato dal cubito reale egizio. Per quanto riguarda le misure di superficie, in particolare per definire la grandezza di un terreno, ci si avvaleva del setat. Esistono varie frazioni del setat, la più piccola delle quali è il cubito che è pari a 1/100 setat (il nome di cubito deriva dal fatto che corrisponde a una striscia di terra d'un cubito in larghezza e una canna ‒ ossia 100 cubiti ‒ in lunghezza). Unità base di capacità era il barile o heqat, quella ponderale il deben, benché il peso dei metalli pregiati sia espresso anche in kite. Definire principi unitari nella metrologia egizia è problematico; non sembra che le diverse misure (lineari, ponderali e di capacità) fossero tra loro strettamente collegate, soprattutto nel rapporto tra misure di lunghezza e di capacità e in quello tra misure di capacità e di peso. L'eccezione è rappresentata, nel primo caso, dall'heqat equivalente a 1/20 del cubito corto e, nel secondo, dal deben che equivale approssimativamente a 1/50 heqat d'acqua. Inoltre esse non appaiono bene articolate rispetto alla numerazione: questa è decimale, mentre i multipli e sottomultipli delle varie misure si ottengono con fattori che sono ora 10 e le sue potenze (1 canna = 100 cubiti), ora 6 e i suoi multipli (1 cubito = 6 palmi = 24 dita), ora 2 e le sue potenze, come nel caso del frazionamento dell'heqat in subunità secondo la scomposizione dell'Occhio di Horus, con un metodo usato nell'aritmetica per realizzare le moltiplicazioni (mediante duplicazioni successive) e le divisioni. Va infine rilevato che, nell'economia dell'antico Egitto, non basata sul libero mercato ma regolata dall'amministrazione centrale, alcune forme di remunerazione prevedevano una quantificazione necessariamente legata al peso; si utilizzavano come denaro pezzature standard di metalli preziosi oppure semplici sacchi di granaglie (orzo o farro) di peso predefinito che venivano usati come merce di scambio o come forma di paga. Queste quantità potevano essere convertite in argento o rame secondo un cambio fisso. Ad esempio, i due caposquadra e lo scriba di Deir el-Medina ricevevano 2 sacchi d'orzo e 5,5 sacchi di farro al mese; gli operai 4 sacchi d'orzo e 1,5 di farro, gli apprendisti 1,5 sacchi di orzo e mezzo di farro. Un sacco conteneva circa 77 l di granaglie; il rame veniva quantificato in deben, mentre l'argento era pesato in sbenati (7,6 g) o kite (9,1 g). Il rapporto tra il valore dei metalli e delle granaglie era peraltro soggetto a oscillazioni notevoli. Un ostrakon risalente alla XX Dinastia illustra come avvenivano gli scambi commerciali nel villaggio di Deir el-Medina; esso riferisce "quanto verrà dato a Paidehu in pagamento per una brocca di rame: 10 deben di rame; 5 hin (2,5 l) di olio di sesamo, per un controvalore di 1 deben per ogni hin, che fanno 5 deben; una tunica di stoffa liscia, che fa 5 deben; due sacchi di cuoio, fanno 4 deben; 4 stuoie, fanno 2 deben; 4 hin di olio balsamico, fanno 2 deben. Totale: 28 deben di rame, resto: 9 deben". Dunque l'acquirente corrisponde parte del suo pagamento con prodotti per la cui quantificazione si ricorre al calcolo in deben di rame. *
Bibliografia
F.G. Skinner, Pesi e misure, in Ch. Singer et al., Storia della tecnologia, I, Torino 1966² (trad. it.), pp. 786-89; S. Vleming, s.v. Masse und Gewichte in den demotischen Texten, in LÄ, III, coll. 1209-214; A. Pichot, La nascita della scienza. Mesopotamia, Egitto, Grecia antica, Bari 1993, pp. 182-84; M. Gutgesell, Economia e commercio, in R. Schulz - M. Seidel (edd.), Egitto. La terra dei faraoni, Köln 1997, pp. 371-72; M.A. Powell, s.v. Weights and Measures, in ANE, V, pp. 339-42 (con bibl.).
Mondo fenicio e punico
di Lorenza-Ilia Manfredi
I sistemi lineari e ponderali
I sistemi di misurazione in vigore nelle città della Fenicia e nel mondo punico d'Occidente sono poco conosciuti nella loro articolazione. Quattro le unità di capacità documentate in Fenicia: il lg, di 0,6 l circa, attestato al singolare in un'iscrizione di Tiro (RÉS 1204, 2) e forse al plurale in un ostrakon fenicio di Saqqara; lo s'h, probabilmente corrispondente al seāh biblico di 13 l e riconosciuto nell'abbreviazione s incisa su un coperchio di anfora dell'VIII sec. a.C. da Tiro; il kd documentato in un'iscrizione fenicia rinvenuta a Ialisos a Rodi del 750 a.C. e rapportato al kd ugaritico di 22 l circa; il mslt ripetuto su tre recipienti d'alabastro rinvenuti a Cartagine e ancora di valore indeterminato. Maggiormente articolata la documentazione riguardante i sistemi lineari. In Fenicia e nelle regioni limitrofe sono attestati i cubiti egiziani di 0,55 m (cubito reale o "lungo") e di 0,45 m (cubito "corto") e quello di tradizione biblica di 0,56 m. Una pluralità di unità di misura è attestata anche nell'Occidente punico con un interessante fenomeno di continuità in epoca romana. La mensa mensuraria di Leptis Magna del III sec. d.C. riporta tre diverse unità di misura: il piede romano di 0,29 m; il cubito punico di 0,51 m; il cubito egiziano di 0,52 m. Allo stesso modo, nei monumenti romani della Mauretania sono stati individuati e riportati nell'ambito della tradizione fenicia d'Occidente il cubito di 0,55 m e quello di 0,46 m (in rapporto di 6:5). Quest'ultimo, in particolare, è ampiamente documentato nell'edilizia cartaginese e neopunica del Nord Africa, della Sardegna, della Sicilia e della Penisola Iberica. Complessa e di non facile lettura è la documentazione relativa ai sistemi ponderali fenici e punici: non si hanno, infatti, fonti dirette o indirette che forniscano elementi utili alla ricostruzione dei valori teorici su cui si basavano i sistemi ponderali delle città dell'Oriente e Occidente fenicio. Dalle iscrizioni si deduce soltanto che il siclo (šql ) è l'unità di peso fenicia e punica principale, e scarsa e di difficile interpretazione è la documentazione relativa ai sui multipli e sottomultipli. Tuttavia, sembra plausibile ipotizzare che con il termine siclo si intendessero diverse misure a cui si affiancavano unità e sistemi designati con nomi e pesi differenti. La diversificazione ponderale emerge in modo evidente dall'esame dei pesi-campione rinvenuti in Fenicia. Emblematica è, a tale proposito, la documentazione di Tiro dell'VIII sec. a.C., nella quale i pesi in bronzo di forma quadrata con la lettera ḥet documentano la contemporanea adozione del sistema compreso tra 8,02 e 8,42 g, probabilmente legato al siclo babilonese di 8,42 g, e quello oscillante tra 10,23 e 10,69 g, che sembra avvicinarsi maggiormente ai sicli attestati ad Arado (10,65 g) e a Tarso (10,45 g) durante la dominazione persiana. Inoltre, nella regione di Tiro sono stati rinvenuti pesicampione di forma diversa, ancora dell'VIII sec. a.C., che potrebbero rifarsi allo šql ṣdn "siclo di Sidone", di 11,26-12,74 g, legato forse al siclo hittita di 11,75 g o a quello ebraico di 11,33 g, per il quale è difficile stabilire eventuali punti di contatto con lo 'bn ṣr, "unità (ponderale) di Tiro", documentata in un'epigrafe del centro e risalente al medesimo orizzonte cronologico (RÉS 1204, 2). Meglio documentata risulta la situazione fenicia di epoca ellenistica. Tre le unità ponderali attestate: 8,5 g circa; 9,5 g circa; 10,5 g circa. I dati di questo periodo si riferiscono essenzialmente alla regione di Arado dove è accertata l'adozione del piede di 9,25-9,5 g, probabilmente legato al siclo siriano. Per la città sembra ipotizzabile l'utilizzo di sistemi diversi basati su unità di 9,97-10,81 g e di 11,96-14,36 g. Quest'ultimo piede, in particolare, potrebbe riferirsi al siclo attestato ad Hamat nell'VIII sec. a.C. o al siclo monetario fenicio di 14 g. Nei pesi-campione fenici databili all'epoca ellenistica diventa evidente l'apporto dei sistemi ponderali greci che determina il progressivo allineamento del siclo alla mina, anche se di fatto sembra prevalere l'equivalenza tra didramma e siclo: ancora nella regione di Tiro, sono stati rinvenuti pesi in bronzo rapportabili ad un piede di 8,29-9,91 g e pesi in piombo con iscrizione in greco, legati ad un'unità di 8,9-9,3 g. Per quanto riguarda il sistema monetale adottato dalle città fenicie a partire dalla metà del V sec. a.C., è prevalente il piede di 7,76 g (siclo fenicio) con una maggiore diffusione di quello pesante di 14 g circa, piuttosto che quello leggero di 7 g circa. Soltanto Arado conia costantemente sul piede microasiatico (siclo di 11,75 g), mentre nelle prime coniazioni di Biblo è forse riconoscibile l'utilizzo del piede siriano di 9,4 g. Il piede attico di 4,36 g compare solamente nel IV sec. a.C. a Sidone e Tiro in corrispondenza della rivolta contro i satrapi. I sistemi ponderali premonetali vicino-orientali, il microasiatico di 5,8 g e forse il siriano di 9,4 g, giungono in Occidente già nell'XI sec. a.C. seguendo le rotte commerciali che passando per Cipro toccano la Sardegna e la Penisola Iberica. Il piede fenicio di 7,76 g si diffonde più tardi, dopo essersi affermato lungo tutta la costa siriana, e si inserisce in un contesto occidentale in cui il piede microasiatico aveva avuto un'ampia e capillare diffusione soprattutto tra il VI e il V sec. a.C., quando comincia ad essere sostituito da quello euboico-attico. In ambito punico, i due piedi di origine orientale sembrano integrarsi formando, almeno secondo i dati che emergono dall'esame delle monete cartaginesi e in particolare di quelle in bronzo testa maschile/cavallo al galoppo e kore/cavallo dietro palma della prima metà del IV sec. a.C., un sistema misto aperto al confronto con le unità di tradizione occidentale. Testimonianza in tal senso è fornita dall'iscrizione dedicatoria rinvenuta a San Nicolò Gerrei in Sardegna del II sec. a.C. (IFP, pp. 91-92, n. 9) in cui compare l'espressione mzbḥ nḥšt mšql lṭrm m't 100, "altare di bronzo del peso di 100 litre", dove il termine lṭr è inteso come litra, unità ponderale di origine greca, documentata anche a Cipro in un'iscrizione fenicia di Lapethos del 345-315 a.C. Allo stesso modo, le più antiche coniazioni puniche in argento (410 a.C.) risultano battute sul piede euboico-attico, mentre le serie in oro ed elettro sono coniate sul siclo fenicio di 7,76 g. Di notevole interesse è la possibile adozione per le serie in oro del 350-320 a.C. dell'unità di origine siriana di 9,4 g, forse riconoscibile anche nel sistema ponderale di 8-9 g utilizzato per le emissioni ispano-cartaginesi di età barcide e per quelle delle città neopuniche di Malaga, Gadir, Ebusus. Dalla fine del III sec. a.C. nella Penisola Iberica è attestata anche l'unità di 10-11 g, ritenuta di tradizione cartaginese, ma che potrebbe anch'essa ispirarsi a sistemi di origine orientale. La mancanza di uno studio comparato dei pesi-campione provenienti da Cartagine e dalle regioni puniche non permette di valutare la dinamica formativa ed evolutiva dei sistemi ponderali commerciali e il loro rapporto con quelli monetali sviluppatisi nell'Occidente punico. Tuttavia, la documentazione dei pesi ritrovati ad Ibiza sembra confermare la notevole influenza locale sui sistemi ponderali adottati nelle diverse aree puniche, a riprova della costante volontà delle città di origine fenicia prima, di Cartagine e quelle neopuniche poi, di integrarsi e interagire attivamente con le realtà economiche con cui erano in relazione. I pesi-campione provenienti da Ibiza, infatti, datati all'VIII sec. a.C., pur presentando evidenti affinità formali ed epigrafiche con i coevi pesi rinvenuti in Fenicia, non ne condividono i valori ponderali. Tale dicotomia sembra rapportabile a un fenomeno generale che documenta, a fronte di una diversificazione ed evoluzione ponderale, una continuità tra Oriente e Occidente nella terminologia adottata per indicare la quantità di metallo non monetato e le monete. Un esempio in tal senso è rappresentato dal termine prs attestato nei testi ugaritici, aramaici e fenici per indicare la mezza mina e messo in relazione all'accadico parīsu, corrispondente a mezzo kōr. Il nome ricompare su una moneta tripolitana di Oea del I sec. a.C. nell'espressione prz mš e su un ostrakon della regione di Msellata del I sec. d.C. (IPT, 86) in riferimento al valore di cinque prṣm. In entrambi i casi il termine è stato interpretato come il nome della stessa moneta. Ancora la leggenda prš šlš compare sulle emissioni attribuite dubitativamente alle isole della Tunisia del II-I sec. a.C. La seconda parola šlš è il numerale 3, che potrebbe indicare il valore della moneta equivalente a 3 prš. In questa prospettiva è interessante notare la presenza sulle monete di Tiro del 450 a.C. del termine šlštn interpretato, sia pure dubitativamente, come trentesima parte di mina. Lo stesso processo che vede l'utilizzo della medesima terminologia per indicare pesi e monete è riscostruibile per il kkr, "talento" messo in relazione, in Fenicia, con il krš persiano di 83,33 g, riconosciuto nel kr dell'iscrizione fenicia di Lapethos (KAI 43, 14) della fine del III sec. a.C. in cui compare l'espressione b k(ṣ)p mšql kr 100 w 2, "in argento del peso di 102 kr", e attestato nell'Occidente fenicio fino al I sec. d.C. Il termine, infatti, compare nell'iscrizione punica CIS I, 17,4 e in un ostrakon neopunico della Tripolitania. Ma il nome qr compare anche nell'iscrizione di Kition CIS I, 86 datata alla prima metà del IV sec. a.C., dove indica la maggiore delle tre unità monetali citate: il qr, forse il didramma; qp', tetrobolo; p', obolo. La documentazione punica d'Occidente, infine, testimonia sulle emissioni in elettro, argento e bronzo che si pongono tra il 264 e il 237 a.C. numerali e lettere interpretati come indici del valore della serie di riferimento o, nel caso delle monete enee, come il rapporto del bronzo rispetto all'argento. In particolare, la zayn, presente sulle emissioni in elettro della rivolta libica, in bronzo della Sardegna e della Penisola Iberica, è stata messa in relazione con il termine zr, attestato nelle tariffe sacrificali cartaginesi del IV-III sec. a.C. e interpretato come nome di una moneta dal valore di 1/8 di siclo. Nella Tariffa di Marsiglia, accanto allo šql è anche documentato il 'grt, ritenuto un nominale di valore inferiore allo zr, comparato allo āgorāh di tradizione ebraica e riconosciuto anche in contesto spagnolo con il valore di un obolo. Non sono documentati, né in ambito fenicio né punico, regolamenti o controlli di fabbricazione degli strumenti e delle operazioni di pesatura simili a quelli attestati in ambito greco. Tuttavia, in Fenicia è stata rinvenuta una tessera di controllo di bronzo risalente all'VIII sec. a.C. che riporta un'iscrizione con il presunto toponimo di una dogana posta sulle montagne dell'Amano, per la quale è stato ipotizzato un utilizzo come sigillo per i sacchi di metallo prezioso già controllato. Interessante è anche l'attestazione su un'iscrizione fenicia, databile tra la metà del IV e l'inizio del III sec. a.C., rinvenuta ad Atene (Pireo) e sul più tardo testo neopunico della Tripolitania (IPT 37, 16-17), del termine lmḥt, "legale", riferito a monete diverse per definirne il corso autorizzato e controllato. Al controllo della produzione monetale erano preposti, almeno nell'Occidente punico secondo la documentazione epigrafica e numismatica dalla fine del IV sec. a.C., i mḥšbm, "controllori" finanziari cartaginesi. Dai testi e ancora dalle monete neopuniche degli emporia della Tripolitania emergono altre magistrature locali con il ruolo di garanti del valore delle monete battute dalla zecche cittadine, tra cui il mpqd, "tesoriere, responsabile della zecca", di Leptis Magna alla fine del I sec. a.C.
Bibliografia
Sui sistemi di capacità, lineari e ponderali in Oriente:
P. Bordreuil, s.v. Métrologie, in DCPP, pp. 291-92; A. Ben-David, The Hebrew-Phoenician Cubit, in PEQ, 1978, pp. 27-28; M. Heltzer, Some Questions of the Ugaritic Metrology and its Parallels in Judah, Phoenicia, Mesopotamia and Greece, in UgaritF, 21 (1989), pp. 195-208; J. Elayi - A.G. Elayi, Recherches sur les poids phéniciens, Paris 1997; L. Sole, Nuove considerazioni sull'unità ponderale della prima serie monetale di Biblo, in Transeuphratène, 20 (2000), pp. 45-60.
Per gli sviluppi in Occidente:
A. Jodin, Recherches sur la métrologie du Maroc punique et hellénique, Tanger 1975; E. Acquaro, Tharros tra Fenicia e Cartagine, in CFP II, pp. 547-58; P. Barresi, Sopravvivenze dell'unità di misura punica e i suoi rapporti con il piede romano nell'Africa di età imperiale, in Africa Romana VIII, pp. 479-502; A. Planas Palau - A. Martín Mañanes, Pesas premonetales de la Ibiza arcaica, Eivissa 1992; L. Villaronga, Metrologia de les monedes antigües de la Península Ibérica, in ActaNum, 28 (1998), pp. 53-74.
Mondo egeo
di Nicola Parise
I sistemi ponderali
Nella Creta minoica le quantità di aridi e di liquidi erano registrate nei documenti in lineare A mediante sequenze scalari come 1 + 1/2 + 1/4 + ... + l/n. Le corrispondenti unità di volume erano rappresentate dagli ideogrammi dei prodotti che venivano misurati: ad esempio, AB 120 per grano, AB 131 per vino. Con lo stesso criterio si registrava il valore delle cose pesate; in questo caso la notazione era preceduta dall'ideogramma della bilancia (AB 118). Non ci sono dati sicuri per determinare la grandezza delle unità degli aridi e dei liquidi. Per i pesi, invece, è stato possibile isolare, fra i materiali recuperati, un'unità (m) di 61,2 g; 61,71 g; 61,94 g; 62,646 g; 66,357 g nota, oltre che a Creta, nelle Cicladi e nel Peloponneso. Le unità secondarie erano calcolate prevalentemente in base a rapporti binari e ternari. Il multiplo secondo 48 (2937,6-3185,136 g) era impiegato come unità speciale per pesare la lana. Non è escluso che i pesi egei potessero essere riscontrati con le unità di 11,75 g; 9,4 g; 7,83 g correnti in Asia Minore, Siria e Palestina, fra le quali, sin dall'antica età del Bronzo, si era venuta instaurando una serie di rapporti di conversione come 4:5:6. Ma, se è così, l'unità fondamentale di 61,2-66,357 g doveva in realtà avere un peso "teorico" tale da corrispondere agevolmente ai valori orientali. Ad esempio: (65,27 g × 360) = (11,75 g × 2000) = (9,4 g × 6500) = (7,83 g × 3000). In contrasto con le pratiche minoiche, per registrare le diverse partite di aridi e di liquidi e delle cose valutate a peso, la ragioneria dei palazzi micenei faceva uso di un insieme strutturato di misure di peso e di capacità, quasi integralmente ricostruito sulla base dei testi in lineare B che riferiscono somme di quantità frazionarie. Le unità superiori degli aridi e dei liquidi continuavano ad essere rappresentate dagli ideogrammi dei prodotti registrati (ad es., *121, HORDEUM, per orzo; *130, OLEUM, per olio) e si dividevano in decimi (*112, T) per i primi ed in terzi (*113, S) per i secondi. Altre due unità rappresentate da segni comuni ad entrambe le serie (*111, V; *110, Z) avevano rispettivamente il valore di 1/6 di T o di S e di 1/4 di V. Così, per x e y uguali ad un'unità di aridi (a) o di liquidi (b), si avevano le equivalenze seguenti:
a) x = T 10 = V 60 = Z 240;
b) y = S 3 = V 18 = Z 72.
In seguito alle misurazioni del vasellame rinvenuto a Pilo è stato possibile suggerire per ciascuna misura i valori assoluti riportati di seguito:
a) x = l 96; b) y = l 28,8
T = l 9,6; S = l 9,6
V = l 1,6
Z = l 0,4
La maggiore delle unità di peso era rappresentata, invece, dall'ideogramma della bilancia *118 (L). Essa si divideva in 30 unità rappresentate dall'ideogramma *117 (M) ed ognuna di queste in 4 rappresentate dall'ideogramma *116 (N):
Per analogia con i sistemi ponderali orientali le unità di L, M, N sono state identificate con quelle del talento, della mina "pesante" e della mezza mina "leggera". Più incerta appare, invece, la determinazione delle misure minori (*115-*114, P-Q). Comunemente si ritiene che P debba essere considerato 1/12 di N e Q 1/6 di P. Ma non c'è niente di certo. La proposta di assegnare a P il valore di 1/60 di M o di N non ha finora trovato conferma. Un'unità speciale uguale a 1/10 di L era adoperata per pesare la lana (*145, LANA). Nei testi di Cnosso i segni sillabici RO e QI ricorrevano con lo stesso valore di N e di Q. Per definire i valori assoluti delle diverse unità è stato attribuito al talento il peso di 29 kg corrispondente a quello del tronco di piramide di gesso rossastro rinvenuto nelMagazzino 15 del Palazzo di Cnosso, ricostruendo la seguente scala di misure:
Ma, una volta accertato che il gesso di Cnosso era un'ancora votiva e non un peso, tutto è tornato ad essere oggetto di discussione. È stata avanzata, allora, l'ipotesi che il sistema ponderale miceneo dovesse essere il risultato di un riordinamento di vecchie unità minoiche in base a nuovi rapporti, secondo l'esempio dei criteri di organizzazione delle misure in uso nel Vicino Oriente antico. Di fatto il valore di m non era mai stato dismesso, anzi esso avrebbe mantenuto un ruolo importante fin nello scorcio della tarda età del Bronzo. E così, per m = 65,27 g, si è potuto redigere il prospetto seguente:
Imprecisati restano i pesi delle unità minori. La conversione con le misure d'Asia Minore, Siria e Palestina si faceva come per il passato, essendo 360m pari ai 3/4 del nuovo talento.
Bibliografia
A.J. Evans, Minoan Weights and Mediums of Currency from Crete, Mycenae and Cyprus, in Corolla numismatica, London 1906, pp. 336-67; A. Segrè, Metrologia e circolazione monetaria degli antichi, Bologna 1928, pp. 160, 175; E.L. Bennett, Fractional Quantities in Minoan Bookkeeping, in AJA, 54 (1950), pp. 204-22; M. Lang, The Palace of Nestor. Excavations 1963. II, Pylos Pots and the Mycenaean Unit of Capacity, in AJA, 68 (1964), pp. 99-105; A. Sacconi, Gli ideogrammi micenei per le cifre ed i segni di misura, in Kadmos, 10 (1971), pp. 135-49; M. Ventris - J. Chadwick, Documents in Mycenaean Greek, Cambridge 1973², pp. 53-60, 393-94; G.F. Bass (ed.), Cape Gelidonya. A Bronze Age Shipwreck, Philadelphia 1977, pp. 136-37; K.M. Petruso, Lead Weights from Akrotiri. Preliminary Observations, in C. Doumas - H.C. Puchelt (edd.), Thera and the Aegean World, I, London 1978, pp. 547-53; Id., Reflections on Cycladic and Minoan Metrology and Trade, in J.L. Davis - J.F. Cherris (edd.), Papers in Cycladic Prehistory, Los Angeles 1979, pp. 135-52; J. Chadwick, Il mondo miceneo, Milano 1980 (trad. it.), p. 142; N.F. Parise, Unità ponderali egee, in M. Marazzi - S. Tusa - L. Vagnetti (edd.), Traffici micenei nel M editerraneo. Problemi storici e documentazione archeologica, Taranto 1986, pp. 303-14; K.M. Petruso, Keos VIII. Ayia Irini. The Balance Weights. An Analysis of Weigh Measurement in Prehistoric Crete and the Cycladic Islands, Mainz a. Rh. 1992.
Mondo greco
di Annalisa Polosa
I sistemi ponderali e i sistemi lineari, di superficie e di capacità dall'età arcaica all'ellenismo
I sistemi ponderali
La determinazione delle misure di peso, come quella delle altre misure, ha come origine una serie di criteri soggettivi: l'unità fondamentale del sistema ponderale greco, il talento, corrisponde, oltre che al termine con il quale si indica il piatto della bilancia, alla quantità del carico che un uomo in marcia poteva sopportare. È evidente che ad altre culture corrispondevano altri parametri, così il corrispettivo del talento greco era, altrove, il carico di un cammello o di un asino. I termini utilizzati per individuare le unità di peso sono talvolta una spia delle origini geografiche e culturali di questa, come è per la mina (mna), termine che ne denota l'origine orientale. Altrove segnalano la funzione premonetaria di alcuni oggetti, come l'obolo (obelos), sesta parte di una manciata (drax, da cui deriva il termine drachmè) di spiedi utilizzati nelle pratiche di sacrificio e di spartizione rituale delle carni. In molti casi, i termini utilizzati per indicare i valori ponderali sono gli stessi che definiscono le unità monetarie. L'identità fra i termini adoperati per le unità ponderali e quelli che identificano le monete non sempre corrisponde a un'identità di peso: questo perché mentre i sistemi ponderali hanno la tendenza ad una forte stabilità, la monetazione è soggetta in prosieguo di tempo a manipolazioni determinate da fattori economici, perciò i due sistemi tendono a discostarsi. Così, un'identità reale tra pesi e monete è verificabile soltanto in determinate situazioni e spesso si può constatare l'esistenza contemporanea di due diversi sistemi, uno commerciale e uno monetale, come ci lascia supporre l'indicazione specifica della materia misurabile apposta sui pesi-campione, specialmente per i metalli preziosi. Le prime menzioni di misure ponderali nella letteratura si trovano nei poemi omerici, dove compare il talento d'oro (Chrysoio talanton), generalmente nella descrizione dei premi nelle gare. Ovviamente, la ricostruzione del peso teorico del talento omerico può farsi soltanto in base al confronto con pesi noti provenienti da contesti culturalmente e cronologicamente affini. Le classi di testimonianze in base alle quali possiamo ricostruire gli antichi sistemi ponderali sono quindi rappresentate dalle fonti letterarie, dai pesi-campione e dalle monete. Nella storia dei sistemi ponderali è a lungo invalsa la tendenza a considerare quelli greci come derivati da unità di misura vicino-orientali. Più recentemente i precedenti dei sistemi in uso in Grecia dall'età arcaica sono stati ricondotti piuttosto ad archetipi definiti "egei". La scarsità dei materiali disponibili per un esame ed un corretto riconoscimento delle unità per il periodo miceneo obbliga comunque a risalire all'età e alla cultura minoica, con tutte le conseguenze storiche e culturali che ciò comporta in termini di riconoscimento di continuità e cesure nel passaggio tra le due epoche. Il sistema ponderale miceneo è parzialmente ricostruibile in base alle testimonianze forniteci dalle tavolette in lineare B degli archivi palaziali. Le unità micenee, indicate mediante i segni 118-114 e trascritte convenzionalmente con le lettere L-Q, sono legate in un sistema di rapporti che, sulla base di alcuni elementi, sembra essere fondato sul sistema sessagesimale in uso nel Vicino Oriente antico. Più recentemente si comincia a comprendere che il sistema miceneo altro non è che il risultato di un adattamento, in base a nuovi rapporti, di precedenti unità minoiche, mai soppiantate e rimaste in uso nella pratica degli scambi sino alla fine dell'età del Bronzo e convertite regolarmente nei contemporanei valori correnti di Siria, Palestina, Anatolia. È quindi più giustificato adesso supporre che i piedi ponderali greci abbiano le proprie radici, piuttosto che da mine e sicli mesopotamici, nella civiltà egea. In Lidia, al tempo di Creso (561-546 a.C.) è in uso un sistema bimetallico. Per l'oro esistono due stateri, uno pesante, probabilmente più antico, di 10,7 g, e uno leggero di 8,05 g, entrambi divisi in terzi (trite), sesti (hecte) e dodicesimi. Il piede ponderale dello statere d'argento è contemporaneo e uguale a quello pesante dell'oro, con un peso che si attesta fra 10,4 e 10,7 g; vengono battuti emistateri di 5,35 g fino al periodo achemenide, per circa un trentennio dopo la morte di Creso. In Persia sono in uso il piede di 8,35 g per il darico aureo e quello di 5,23-5,36 g per il siclo (siglos) d'argento. A.S. Hemmy (1938) propone di vedere due diversi standard per l'argento, uno pesante di 5,36 g e uno leggero di 5,23 g, il primo da mettere in rapporto con il darico, il secondo con lo standard ponderale di Creso. I principali sistemi ponderali in uso in Grecia e nelle aree soggette alla colonizzazione greca sono quello attico, quello eginetico e quello corinzio. Il sistema attico è stato introdotto in Attica, come pare, da Solone e probabilmente è di derivazione euboica (ragione per cui viene denominato "euboicoattico"). È quello meglio conosciuto, ma non è certa la sua derivazione da sistemi ponderali orientali noti. Nel sistema attico, il talento si divide in 60 mine, ciascuna formata da 100 dracme; la dracma, a sua volta, è divisa in 6 oboli:
Il peso teorico di 4,36 g della dracma attica, ottenuto calcolando il punto di addensamento (e non il peso medio) degli esemplari studiati a tale scopo, è confermato da un passo di Livio (XXXVIII, 38) che equipara il talento attico a 80 libbre romane di 327 g circa. Sulla base del peso della dracma attica di 4,36 g si possono così ricostruire i valori assoluti:
talento 26,19 kg mina 436,6 g dracma 4,36 g obolo 0,72 g Accanto alla mina di 436,6 g, che potremmo definire "leggera", esisteva anche una mina di peso doppio (872 g), perciò "pesante", denominata "statere" e utilizzata nella determinazione del peso dell'altra unità monetaria fondamentale greca, lo statere, appunto. Vale la pena di tenere presente il fatto che lo statere può di volta in volta indicare sia la mina pesante, sia l'unità principale dei vari sistemi monetari greci, talvolta del valore di due dracme (didrammi), talvolta del valore di quattro dracme (tetradrammi). Il sistema eginetico, tradizionalmente attribuito a Fidone di Argo, è fondato su un didrammo di 12,32 g; l'articolazione è analoga a quella del sistema euboico-attico:
Nei testi antichi non abbiamo mai una distinzione specifica tra misure eginetiche e misure euboico-attiche. È stato perciò ipotizzato che le unità fondamentali potessero essere le stesse e che la distinzione si verificasse soltanto nel sistema di frazionamento delle unità. Sulla ricostruzione del sistema attico, sulla sua introduzione ad Atene ad opera di Solone e sulla sua posteriorità rispetto al sistema eginetico è tuttavia ancora aperto il dibattito, soprattutto in seguito all'abbassamento della cronologia delle emissioni monetarie di Egina, recentemente ritenute coeve delle più antiche emissioni ateniesi. La riforma di Solone si data all'inizio del VI sec. a.C. ed è alla base del sistema ponderale attico; su di essa conserviamo due tradizioni, quella di Aristotele (Ath. Pol., X) e quella di Androzione (apud Plut., Sol., XV, 4). Secondo Aristotele la riforma consiste, per ciò che concerne i pesi, nel "colmare" la mina formata da 70 dracme portandola al peso di 100 dracme, e per la moneta nello stabilire un talento di 63 mine con una diminuzione del peso della dracma del 5%. La tradizione confluita in Androzione riferisce del passaggio da una mina di 70 dracme ad una di 100, avvenuto non con un aumento di dracme per mina, ma con una diminuzione del peso della dracma. In questo modo la seisachteia (scuotimento dei pesi) avrebbe agevolato i debitori, che restituivano gli importi dovuti in dracme-moneta, più leggere delle dracme-peso, ma non danneggiava i creditori, che avrebbero ricevuto lo stesso valore concesso in prestito, ma in moneta: indizi di una mentalità abituata a pensare in termini di economia monetaria, quale non può accettarsi per l'età soloniana. In conclusione, se la riforma si è attuata nel senso proposto da Androzione, mina e dracma in uso ad Atene prima della riforma sarebbero state eginetiche (mina = 70 dracme di 6,1 g) e dopo la riforma si arriva a una combinazione fra dracma euboica di 4,36 g e mina eginetica di 70 dracme di 6,1 g. Se invece si segue Aristotele, ad Atene già circolava la dracma euboica con una mina leggera di 70 dracme. Più tardi, il decreto di Tisameno (Andoc., De Mysteris, 81-82 e IG II², 1013) del 403 a.C. prescrive il ritorno a leggi, pesi e misure di Solone; secondo Lang (Lang - Crosby 1964) con questo decreto si sancisce il ritorno alla mina di Solone di 105 dracme-moneta; in realtà si tratta di una revisione di leggi. Una legge successiva (IG II², 1013), databile al II sec. a.C., sancisce il passaggio da una mna emporikè di 138 dracme ad una nuova mna emporikè di 150 dracme (tutte di stile nuovo); questa mina, secondo L. Breglia Pulci Doria (1985), non valeva per vendere l'argento oppure ciò che si vendeva pagando in moneta. Il provvedimento serve a creare una mina commerciale destinata all'ambito della potenza economica romana. Dunque, le fluttuazioni servono a creare mine di cambio, unità di aggancio con gli altri sistemi ponderali. La caratteristica della fluttuazione nei pesi allo scopo di creare le possibilità di conversione tra sistemi ponderali differenti è particolarmente evidente, se si esamina la testimonianza fornita dalle emissioni monetarie, nella Grecia occidentale. Qui le colonie adottano i sistemi ponderali in uso nelle rispettive città d'origine, ma i sistemi monetari conoscono variazioni degli standard ponderali originate dalle necessità di scambio con le diverse aree in cui si esercitava la loro influenza commerciale. Il sistema monetario adottato dalle città che per prime coniano in Italia meridionale con la tecnica del rovescio incuso (Sibari, Metaponto, Crotone, Caulonia, colonie achee) è comunemente denominato acheo, ma si tratta del sistema cosiddetto "euboico-corinzio", nato a Corinto e diffuso nelle sue colonie e nelle altre zone sottoposte alla sua influenza commerciale. Il sistema corinzio era basato su uno statere di 8,7 g circa, identico allo statere euboico-attico (diffuso in Attica, nelle zone di influenza ateniese e più tardi adottato da Alessandro Magno per tutto il mondo ellenistico); la differenza è nel fatto che nel sistema corinzio lo statere era diviso in 3 dracme di 2,9 g circa, mentre in quello attico lo statere conta 2 dracme di 4,35 g circa. Nelle città achee della Magna Grecia, tuttavia, i valori standard adottati sono leggermente più bassi che nella madrepatria (lo statere pesava 8 g ca., la dracma 2,7 g ca.); è stato supposto che la variazione di peso fra lo statere acheo e quello corinzio corrisponda ad una sorta di tassa di scambio imposta sull'acquisto della valuta achea. A Posidonia e Velia viene adottato per la monetazione il sistema ponderale detto "foceo", basato su uno statere di 7,5 g circa, diviso in due dracme di 3,65 g, in cui è la dracma a costituire l'unità fondamentale, forse per la necessità di adeguarsi al nominale in uso a Velia. A Reggio, colonia calcidese come Naxos e Zancle in Sicilia, che partecipa della circolazione siceliota anziché di quella italiota, il sistema ponderale è calcidese (usato per un certo periodo anche a Cuma e forse in Etruria), basato su una dracma di 5,7 g. Per il sistema calcidese, in uso anche a Naxos, Zancle e Imera, era stata proposta un'identificazione con il sistema eginetico; più recentemente è stata riconosciuta un'origine microasiatica, oppure l'identificazione con il sistema in uso nella madrepatria Calcide. Sulla costa meridionale della Sicilia possiamo riconoscere un'area "del didrammo" (cui partecipano le colonie doriche, fra cui Selinunte e Agrigento, poi Gela e Camarina) che adotta il sistema euboico-attico (o euboico-corinzio) e usa un didrammo di 8,7 g circa. Anche Siracusa imposta le sue emissioni sul sistema euboico-attico usando come base il tetradrammo, fino all'età di Timoleonte quando passa a quello corinzio fondato sullo statere di 8,7 g diviso in 3 dracme di 2,9 g. Con Agatocle si ritorna al sistema attico. Durante le imprese di Pirro si assiste all'emissione di serie d'argento basate sul sistema calcidese con unità di 5,7 g. In Sicilia, tuttavia, era in uso anche un sistema ponderale ancorato inizialmente all'uso monetario del bronzo; adattato all'argento prima della prima metà del V secolo, esso è fondato sull'unità fondamentale della litra, corrispondente ad un obolo eginetico (0,872 g) e rapportata come 1:10 allo statere corinzio; l'unità maggiore del sistema, il nomos, corrisponde al didrammo (dekalitron) di 8,72 g. Il sistema prevede dunque un talento di 104,64 g, composto da 12 nomoi e, quindi, da 120 litrai. Ogni litra si divide poi in 12 once di 0,072 g. Questi valori sono riferibili al sistema dopo che questo conobbe una riduzione al tempo di Dionisio I di Siracusa; in precedenza i nomoi pesavano il doppio, secondo l'ipotesi di H. Mattingly (1943), in contrasto con la testimonianza di Aristotele secondo il quale il talento pesava 24 nomoi. Il passaggio dal talento di 240 litre a quello di 120 viene realizzato attraverso il frazionamento dell'unità in 6 nomoi di 4 dracme ciascuno (nomoi pesanti, che valgono il doppio dei nomoididrammi). Il sistema della litra, come è testimoniato dalle leggi conservate nell'archivio del tempio di Zeus, passa dalla Sicilia a Locri, quando Dionisio I stringe rapporti matrimoniali e politici con l'aristocrazia locrese. Il caso di Locri è particolarmente interessante, perché a quel tempo a Locri non si batteva moneta, quindi il sistema della litra giunse in prima istanza come sistema ponderale. Nell'area tirrenica dell'Occidente mediterraneo sono dunque in uso tra VI e V secolo quattro unità monetarie fondamentali: la dracma calcidese (5,82 g), il piede "fenicio" (7,76 g), lo statere acheo (8,06 g) e il didrammo e il tetradrammo euboico-attici (rispettivamente 8,73 e 17,46 g). Queste unità sono convertibili per mezzo di un sistema di ragguagli e vengono definiti sistemi "misti", come quello in uso più tardi a Cartagine. Un esempio di sistema misto è quello di Crotone, che conia frazioni recanti il tripode al dritto e al rovescio tipi ripresi da quelli di Corinto, di Atene e di alcune città siceliote (Siracusa, Reggio, Messana, Agrigento) e che permettono l'aggancio della valuta crotoniate a quella euboica in uso nei centri citati. Anche a Massalia, che adotta dapprima l'unità focea di 2,29 g, mutuata dalla madrepatria, e in seguito quella "milesia" di 1,29 g, le unità di conguaglio permettono le conversioni con le valute in uso nelle aree verso le quali era rivolta l'attività commerciale della città. Per il riconoscimento dei sistemi ponderali in uso nel mondo greco e orientale durante il periodo ellenistico, la nostra fonte principale è costituita dalle emissioni monetarie. Con il regno di Alessandro il mondo greco-orientale si avvia a superare la molteplicità di sistemi monetari propria dell'ambito egeo e microasiatico e dell'epoca precedente. Alessandro, infatti, al contrario di Filippo che aveva adottato unità ponderali attiche per le serie in oro, ma aveva mantenuto per l'argento lo standard traco-macedone di 14,5 g, decide di tagliare entrambi i metalli sul piede ponderale attico (1 statere aureo = 20 dracme d'argento, con un rapporto di 1:10, e non più epitrito come quello in uso nell'ambito persiano; l'unità di bronzo corrispondeva a 1/8 dell'obolo d'argento). Gli Antigonidi mantengono l'assetto metrologico secondo il sistema ponderale attico fino alla conquista romana, ma abbandonano l'oro come metallo monetario mantenendo solo argento e bronzo, eccezion fatta per la riduzione di 1/12 del peso del tetradrammo da parte di Perseo durante la terza guerra macedonica (171-168 a.C.). Anche i Seleucidi mantengono il sistema monetario ancorato al sistema ponderale attico, eccetto che per l'esperienza della zecca di Babilonia che sotto il regno di Seleuco batte una serie di tetradrammi attici che presto perdono peso attestandosi al valore di 3 sicli persiani (16,8 g): l'emissione è stata interpretata come dedicata al commercio interno in una regione assuefatta al sistema del siclo, ma essa è forse da vedersi come destinata ad un ristrettissimo ambito locale in rapporto al tempio di Baal-Marduk. Anche a Susa e a Ecbatana esiste una serie basata sullo stesso valore ponderale, sempre durante il regno di Seleuco. In Oriente, al di là dell'Eufrate, la zecca di Bactra emette dapprima (dal 289 a.C.) serie basate sul sistema attico, ma intorno al 285 a.C. introduce un piede ponderale indiano di 3,75 g, destinato evidentemente alla circolazione interna della regione. Le emissioni di Antiochia sotto Antioco Epifane segnano una prima disgregazione della valuta fondamentale dell'impero, che in Occidente durante il regno di Alessandro Balas sarà compiuta con le emissioni di piede fenicio (14,2 g) nelle zecche di Acco, Tiro, Sidone, Berytos. Cessano contemporaneamente le emissioni auree, che vengono confinate a occasioni commemorative, mentre aumentano quelle enee, destinate alla circolazione locale. Ad Occidente, erano di piede attico le emissioni d'argento in Bitinia, Ponto, Cappadocia e Pergamo. Qui, probabilmente dopo la pace di Apamea, durante il regno di Attalo I o Eumene II ha inizio la coniazione dei cistofori, battuti su un piede di 12,65 g prossimo a quello rodio (almeno al valore delle monete rodie a quel momento) e che era facilmente convertibile in dracme attiche e in denari romani. In Egitto, dove la conquista macedone aveva coinciso con l'introduzione dell'uso della moneta, le prime innovazioni rispetto al sistema ponderale attico hanno luogo negli anni fra 315 e 313 a.C., quando le serie di Tolemeo mostrano una riduzione ponderale per la dracma, che pesa 3,75 g. Piuttosto che un adeguamento al piede rodio diffuso nei mercati del Mediterraneo orientale, il peso ridotto della dracma sembra essere la conseguenza di un'alterazione del rapporto oro/argento, da 1:10 a 1:10,5 (1 statere aureo = non più 5 tetradrammi d'argento, ma 5 tetradrammi + 1 nuova dracma). Dopo la guerra contro Demetrio Poliorcete (311 a.C.) anche il tetradrammo subisce una riduzione ponderale arrivando al peso di 15,7 g, a testimonianza di una nuova variazione del rapporto oro/argento, stavolta passato a 1:11 (1 aureo = 6 tetradrammi d'argento). Dopo che Tolemeo ebbe assunto il titolo di re a seguito della fallita spedizione di Antigono contro l'Egitto, fu ripresa la coniazione dell'oro, con un peso diverso rispetto a quello tradizionale, di 7,15 g. In questo modo si ristabiliva il rapporto 1 statere aureo contro 5 tetradrammi d'argento sempre secondo la ratio di 1:11. Dopo la battaglia di Ipso assistiamo all'ultima trasformazione del sistema tolemaico: vengono coniati emidracme e pentadrammi (trichrysa) d'oro e tetradrammi e ottodrammi d'argento, con un rapporto tra i due metalli di 1:12 e con un'unità monetaria attestata su valori più bassi del solito, simili a quelli del sistema ponderale fenicio. L'Egitto diviene così un distretto monetario chiuso, contrapposto alle aree di circolazione del piede attico.
I sistemi lineari, di superficie e di capacità
La soggettività che è alla base della determinazione delle misure ponderali è l'iniziale fondamento anche delle altre misure, quelle di lunghezza, di superficie e di capacità. Anche in questo caso, infatti, è l'uomo ad essere il riferimento di partenza e la "misura di tutte le cose", come dice Protagora (fr. 263, 3 Diels) e come testimoniano i termini utilizzati per indicare le misure di lunghezza (ad es., cubiti, palmi, piedi). In relazione all'uomo e alle sue attività vengono stabilite anche le misure itinerarie, per cui le distanze vengono determinate rapportandole alle giornate di marcia, e le misure di superficie, che sono fissate, partendo dalle misure di lunghezza, in base alla quantità di cereali necessari per seminare un campo o all'area arabile dai buoi in un giorno. Questi ultimi due esempi mostrano anche la correlazione fra ordini diversi di misure: misure lineari, misure di capacità e misura del tempo. La soggettività nella determinazione delle misure ha come conseguenza naturale una certa variabilità di queste e rende quindi necessaria la creazione di un sistema che non dipenda più da rappresentazioni concrete (il "mio" dito o il "tuo" piede), ma che si fondi su misure oggettive, astratte e quindi fisse. Un passo in questa direzione può forse vedersi nella creazione, all'interno dell'impero persiano, di misure "regali" che coesistono con quelle "medie" e sono leggermente maggiori rispetto a queste, quasi che la persona del re potesse garantire un punto di riferimento più saldo di quello variabile della moltitudine del popolo. È anche interessante sottolineare che riforme fondamentali in materia di misure vengono riferite all'opera dei più celebri legislatori dell'età arcaica come Solone ad Atene e Fidone ad Argo (su quest'ultimo, Hdt., VI, 127). L'ufficialità delle misure è garantita dallo Stato, attraverso l'opera di magistrati preposti al loro controllo nell'ambito delle loro funzioni nel campo commerciale che consistevano nel misurare e stabilire i confini dei terreni, gestire gli affitti, sovrintendere alla consegna dei cereali all'ammasso pubblico: conosciamo, fra gli altri, gli agoranomoi (Arist., Pol., 1299b, 17) e i sitophylakes (Arist., Ath. Pol., 51, 3), ad Atene sono noti anche i metronomoi (Arist., Ath. Pol., 51, 2), mentre le Tavole di Eraclea testimoniano l'esistenza dei sitagertes (I, 102, 177), chiamati agertes a Tauromenion (IG XIV, 423), e degli oristes che operavano in base alle indicazioni del gametras (Tab. Heracl., I, 2 e 187). Lo Stato provvede anche alla creazione di misure-campione (symbola) sulla base delle quali venivano prodotte le misure legali (sekomata), come testimonia il decreto sulla cura delle misure-campione e sulle repressioni di frodi e abusi (IG II, I, 476). Un decreto da Atene del II sec. a.C. (IG II², 1013) ci informa del fatto che in Attica, in quel periodo, tre serie di misure-campione venivano conservate ad Atene, al Pireo e ad Eleusi. Conosciamo anche l'uso, affermatosi dall'età ellenistica, di esporre pubblicamente mensae lapidee con incavi corrispondenti alle misure ufficiali di capacità e iscrizioni esplicative. Più tardi, un altro esempio di misura legale esposta in luogo pubblico è rappresentato dal "piede" con iscrizione ΠΟΥΣ rinvenuto nell'agorà di Gortina (Inscr. Cret. IV, 411), lungo 29 cm e diviso in 16 frazioni (daktyloi). La relazione tra misure greche e romane è testimoniata da un rilievo da Salamina (Berriman 1953) nel quale è raffigurato di fronte il torso di un uomo con le braccia distese (orgyia, di 112 daktyloi), mentre nel campo è impresso un piede (di 16 daktyloi). Frequentemente le misure-campione recano simboli o iscrizioni (generalmente l'iscrizione demosion accompagnata dall'etnico della comunità) che ne garantiscono l'ufficialità. Come e forse più delle misure ponderali, anche le altre categorie di misure, una volta stabilite, rimangono praticamente invariate per lunghissimi periodi: i termini che compaiono in Omero (plethron: Il., XXI, 407, Od., XI, 577; pygon: Od., X, 517, XI, 25; pous ‒ nella forma composta ekatompedon ‒: Il., XXIII, 164; doron: Od., IV, 109) e in Esiodo ( pechus, pous, doron, spithamè: Op., v. 423 ss.) mostrano la corrispondenza fra i sistemi organizzati dell'età arcaica e quelli citati più tardi da Erodoto (II, 6, 9, 149). Ancora Plinio (Nat. hist., II, 21) ci testimonia dell'identità fra misure di lunghezza dell'ambito greco e di quello romano. Agli influssi teorici, testimoniati dalla persistenza in uso di termini che in Grecia spesso derivano dalle culture orientali e dal sistema di divisione delle unità, corrisponde anche una relazione pratica, che consiste nella creazione di agganci fra i sistemi greci e quelli del Vicino Oriente. Il sistema di misure principale del mondo greco è quello attico, che verrà trasmesso al mondo romano. Nel mondo greco occidentale si afferma invece il sistema dorico, del quale conosciamo le misure di lunghezza e di superficie diffuse in area italiota attraverso la testimonianza delle tavole di Eraclea. Oltre alle misure di superficie, che conosciamo attraverso le disposizioni relative alla divisione della terra, conosciamo anche misure siceliote caratteristiche degli aridi. Un altro sistema di misure diffuso nel mondo greco orientale ellenistico è quello detto filetereo o tolemaico (il nome filetereo deriva dal fatto che i Romani lo trovarono attestato nel regno di Pergamo, che era stato fondato da Philetairos): questo sistema era in uso nelle regioni un tempo soggette al dominio persiano e forse anche in alcune aree dell'Egeo (in particolare a Samo).
Sistema attico - L'unità fondamentale per la misura degli aridi è il medimnos, che equivale a 51,8 l e che è equivalente al peso di 120 mine; il medimno è suddiviso in 6 ekteis di 8,6 l, 12 emiekteis di 4,3 l e 48 koinikes di 1,07 l. L'ekteus sarebbe poi stato usato in età romana con il nome di modius. Il fatto che a partire dal III sec. a.C. le misure greche attiche verranno adottate nel mondo romano permette di determinare il loro valore in base alle equivalenze in rapporto alla libbra romana. I liquidi venivano misurati in base al metretès, che equivale a 39,39 l; esso è diviso in 12 choes di 3,274 l o in 144 kotylai di 0,274 l. Anche qui conosciamo l'equivalenza con le misure romane. Le misure di lunghezza attiche hanno come unità fondamentale il piede ( pous) di 0,296 m. Questo, diviso 4, dà il palaistes (di 0,074 m) e diviso 16 il daktylos (0,0185 m). L'unità maggiore è invece lo stadion, formato da 600 piedi, che misura 177,6 m; questo viene diviso per 6, 60, 100, 120 o 240, 400 per ottenere rispettivamente plethron (29,6 m), akaina o kalamos (1,776 m), bema diploun o bema (1,48 o 0,74 m), e pekus (0,44 m).
Sistema filetereo o tolemaico - Nel sistema filetereo o tolemaico il pous misura 0,35 m; l'unità minore è il suo quarto, il palaistes di 0,0875 m. Lo stadion di 210 m, anch'esso formato da 600 piedi come quello attico, conta 6 plethra di 35 m, 100 orgyia di 2,1 m, e 400 pechoi o cubiti (che costituiscono l'unità di base) di 0,525 m. La misura fondamentale degli aridi è l'artaba, formata da 40 choenikes.
Sistema dorico: misure italiote - Dalle Tavole di Eraclea conosciamo particolari misure di lunghezza in uso nelle colonie greche d'Occidente: l'unità fondamentale è lo schoinos di 35,52 m, diviso in 30 oregmata di 1,184 m; l'oregma è a sua volta diviso in 4 piedi di 0,296 m; conosciamo un'altra unità, il gyes di 16,42 m che equivale a 46,225 schoinoi. Delle misure italiote per gli aridi conosciamo il modios di 8,73 l e lo xestes di 0,545 l.
Sistema dorico: misure siceliote - In Sicilia era in uso per la misura degli aridi un medimno di 52,6 l, composto da 4,5 modii di 11,64 l; il medimno si divideva anche in 12 emiekteis di 4,36 l. L'unità di misura fondamentale per i liquidi era invece il kados, che equivaleva al metretès attico, diviso in 6 prochoi, 12 trimetroi e 36 metroi.
Bibliografia
In generale sui sistemi di pesi e misure:
F. Hultsch, Griechische und römische Metrologie, Berlin 1882²; E. Pernice, Griechische Gewichte, Berlin 1894; C.F. Lehmann-Haupt, s.v. Gewichte, in RE, suppl. 3, 1918, pp. 588-654; O. Viedebannt, Antike Gewichtsnormen und Münzfüsse, Berlin 1923; A. Segrè, Metrologia e circolazione monetaria degli antichi, Bologna 1928; A. Bockh, Metrologische Untersuchungen über Gewichte, Münzfüsse und Masse des Altertums in ihren Zusammenhang, Berlin 1938; L. Breglia, Le antiche rotte del Mediterraneo documentate da monete e pesi, in RendNap, 30 (1955), pp. 211-326; A. Stazio, La metrologia, in C. Del Grande (ed.), Enciclopedia Classica. I, Storia e Antichità, III, 6, Torino 1959, pp. 535- 83; S. Grimaudo, Misurare e pesare nella Grecia antica. Teoria, storia, ideologie, Palermo 1998.
Fonti letterarie sulla metrologia:
F. Hultsch, Metrologicorum Scriptorum Reliquiae, I-II, Leipzig 1864-66.
Per i precedenti orientali e micenei delle misure ponderali greche si vedano i contributi precedenti. Sui sistemi ponderali nella Grecia arcaica e classica:
A.S. Hemmy, The Weight Standards of Ancient Greece and Persia, in Iraq, 5 (1938), pp. 65-81; M. Lang - M. Crosby, The Athenian Agora. X, Weights, Measures and Tokens, Princeton 1964; J.H. Kroll - N. Waggoner, Dating the Earliest Coins of Athens, Corinth and Aegina, in AJA, 88 (1984), pp. 325-40; M. Vickers, The Metrology of Gold and Silver Plate in Classical Greece, in Boreas, 21 (1991), pp. 53-72.
Sui sistemi ponderali in età ellenistica:
O. Mørkholm, Early Hellenistic Coinage from the Accession of Alexander to the Peace of Apamea (366-188 BC), Cambridge 1991.
Sulla riforma di Solone:
D. Foraboschi - A. Gara, Misurare, in G. Maddoli (ed.), L'Athenaion Politeia di Aristotele 1981-1991, Napoli 1994, pp. 285-93.
Decreti ateniesi su pesi e misure e decreti monetari:
D. Lewis, The Athenian Coinage Decree, in I. Carradice (ed.), Coinage and Administration in the Athenian and Persian Empires, Oxford 1987, pp. 53-63; L. Breglia Pulci Doria, Per la storia di Atene alla fine del II sec. a.C. Il decreto sui pesi e misure IG II² 1013, in MEFRA, 97, 1 (1985), pp. 412-30.
Sui sistemi ponderali di Magna Grecia e Sicilia:
H. Mattingly, The Little Talents of Sicily and the West, in NumChron, 6, 3 (1943) pp. 14-20; N. Parise, Il sistema della litra nella Sicilia antica tra V e IV sec. a.C., in AnnIstItNum, 21-22, suppl. 6 (1979), pp. 293-308; G. Le Rider, A propos d'un passage des Poroi de Xénophon: la question du change et les monnaies incuses d'Italie du Sud, in G. Le Rider et al. (edd.), Kraay- Mørkholm Essays. Numismatic Studies in Memory of C.M. Kraay and O.M. Mørkholm, Louvain-La-Neuve 1989, pp. 159-72.
Sui sistemi di misura, superficie e capacità:
H. Berriman, Historical Metrology, London - New York 1953; A. Uguzzoni - F. Ghinatti, Le tavole greche di Eraclea, Roma 1968; L. Dubois, Inscriptions grecques dialectales de Sicile, Rome 1989; P. Mayerson, Measures (μετϱηται) and Donkeyloads of Oil in P. Wisc. II. 80, in ZPE, 127 (1999), pp. 189-92.
Mondo etrusco-italico e romano
di Emanuela Alberti
Sistemi e strumenti delle misure lineari, di superficie e di capacità sistemi lineari, di superficie e di capacità
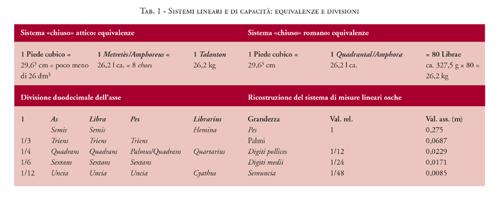
L'importanza del ruolo delle misure nell'Italia antica è attestato dalle numerose rappresentazioni di strumenti e di azioni di misurazione. Tavole di pietra con incisi i campioni di riferimento (mensae mensurariae o ponderariae) sorgevano numerose nei luoghi pubblici delle città, spesso dono di privati cittadini (CIL XI, 5695; V, 6771). Ogni thermopolium disponeva di una propria serie di recipienti standard per misurare vino e altre derrate liquide. La misura accompagnava ogni momento della vita antica e, nel caso specifico di Roma, accompagnava anche il divenire storico della città e dello Stato. Se in un primo momento è Roma, che si andava affacciando allo scenario mediterraneo, ad adeguare il suo sistema metrico a quello più diffuso nel mondo ellenistico, cioè quello attico, saranno poi gli altri popoli della penisola e dell'Impero a mutuare le misure romane, accanto a o in sostituzione delle tradizioni metriche locali. In ambito italico, per quanto è possibile giudicare, le diverse misure convissero fino all'età augustea, quando la pressione ufficiale determinò una romanizzazione completa del sistema metrico. In ambito provinciale, dove i sistemi metrici locali vantavano tradizioni secolari se non millenarie, soprattutto nel settore orientale dell'Impero, le soluzioni adottate furono molteplici, determinando il più delle volte l'uso contemporaneo dei diversi sistemi. Per Roma impiantare una viabilità, colonizzare territori, costruire mercati e presidi significava in primo luogo riordinare la realtà secondo i propri canoni, commisurarla alle proprie necessità e ai propri standard, codificarla, conoscerla: la misura, riduzione del mondo in quantità note, è strumento dell'Impero. Le conoscenze attuali relative alla metrologia in uso presso le diverse popolazioni della penisola prima della diffusione del sistema romano sono piuttosto incerte, anche se non mancano del tutto dati al riguardo, soprattutto per l'ambito osco ed etrusco. La differenziazione metrologica regionale in origine doveva essere piuttosto forte, come emerge da diversi tipi di documentazione di misure di lunghezza, di capacità e di peso. Il sistema metrico romano di età storica, così come può essere ricostruito sulla base delle fonti e della documentazione archeologica, si presenta, alla fine del suo processo formativo, come un sistema "chiuso", in cui le unità di misura ponderali, lineari e volumetriche hanno rapporti ben precisi e definiti tra loro. Tale situazione è il frutto dell'adattamento del sistema di misura locale a quello attico, ampiamente diffuso e perciò ottimo medium verso il sistema di scambi mediterranei, avvenuto secondo modi e tempi che non sono sempre facili da cogliere. Alcune particolarità del sistema romano, probabilmente dovute a persistenze delle tradizioni locali, possono fornire elementi utili alla ricostruzione del quadro originario. Parte integrante dell'atticizzazione è l'assunzione di misure "naturali" di matrice empirica, quali il piede e lo iugero, all'interno di un sistema strutturato più complesso e astratto. Non tutte le grandezze attiche trovano un equivalente diretto nel sistema romano: il talento, la mina e lo statere non sono introdotti affatto, così come lo stadio; la dracma lo è solo in un secondo momento. Accanto ai fondamenti empirici e in combinazione con gli apporti attici, rimane fondamentale la struttura di calcolo originaria, che vede le tre unità di misura di peso, di lunghezza e di capacità (la libra, il pes e l'antico librarius) equiparate tra loro e con la prima unità monetale (as), e divise tutte secondo un medesimo sistema duodecimale (Tab. 1).
Misure lineari e di superficie e relativi strumenti
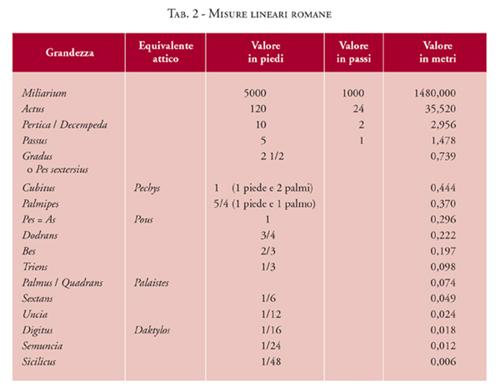
Nell'ambito dei sistemi lineari e di superficie, il sistema romano mostra le tracce dell'adattamento di misure locali, "naturali", al più strutturato sistema attico. Come in gran parte del mondo antico, la base originaria è antropometrica: l'unità fondamentale di ogni misurazione è il piede o pes, diviso in palmi e digiti; le grandezze maggiori sono calcolate in passi e in cubiti. Il piede diffuso in ambito osco è lungo 27,5 cm. In ambito romano, viene adottato il piede attico di 29,6 cm, con un'organizzazione di multipli e sottomultipli a base duodecimale che riflette la tradizionale divisione librale: di fatto, il piede è equiparato all'asse. Per le distanze, i multipli utilizzati sono soprattutto il passus e l'actus. La misura itineraria per eccellenza sono 1000 passi (miliarium o milia passuum, pari a 5000 piedi), equiparati a 8 stadi e 2 plethra (cioè 8 stadi e 1/3) in piedi attico-romani, o a 8 stadi di piedi alessandrini. In ogni caso, il sistema dello stadio greco non è introdotto in Italia (Tab. 2). Il piede è il riferimento anche per le dimensioni di superficie: l'unità più usata è lo iugero, pari a 240 × 120 piedi, con i suoi multipli (heredium, centuria, saltus). L'uso predilige una grandezza "naturale" come lo iugero (pari in origine all'estensione di terreno arabile in un giorno di lavoro da un giogo di buoi) alle grandezze come il versus (di cui il vorsus è la versione in ambito osco) pari a 10.000 piedi quadrati ed equivalente all'attico plethron (Varro, Rust., 1, 10, 1-2; Colum., 5, 1) (Tab. 3). L'importanza che tali misure hanno rivestito nel mondo antico, nel suo paesaggio e nei suoi monumenti, è grandissima, data l'intensa attività costruttiva e colonizzatrice di Roma. Le strade romane con i loro miliari, le divisioni ancora visibili nell'agro centuriato, le proporzioni delle più diverse realizzazioni architettoniche, sono una viva testimonianza dei fondamenti metrici dell'attività romana. A titolo d'esempio, le maglie della centuriazione individuabili tra Lazio e Campania (nella Pianura Pontina meridionale e presso Terracina e Cures Sabini) riflettono le diverse soluzioni adottate dagli agrimensores romani. Gli impianti urbani delle città di Pompei e di Ercolano, nelle diverse fasi, illustrano a livello architettonico e metrico il passaggio da un ambiente culturale osco a uno romanizzato: l'impianto originario delle due città, risalente all'età sannitica (III sec. a.C.), è modulato sulla base del piede osco; le realizzazioni successive alle deduzioni coloniali d'età sillana, soprattutto a partire dall'età augustea, sono basate sempre più sul piede romano. Sempre in Italia, si è visto che sono stati progettati secondo moduli architettonici basati sul piede romano, tra gli altri, il Foro e il Comizio di Paestum (III sec. a.C.), il tempio di Giunone a Gabi e il tempio di Portunus al Foro Boario a Roma (II sec. a.C.), il tempio cosiddetto "dorico-corinzio" (detto anche "della Pace") a Paestum (fine II - inizio I sec. a.C.), il tempio di Venere a Baia, molti insiemi di Villa Adriana a Tivoli, la Basilica Ulpia, la Colonna Traiana (II sec. d.C.), le Terme di Caracalla (III sec. d.C.) e il mausoleo di Massenzio (IV sec. d.C.) a Roma. Squadre (normae) e righe (regulae) costruite e graduate sulla base del piede romano e delle sue partizioni, spesso realizzate in metallo e pieghevoli, sono documentate in gran numero soprattutto da Pompei, Ercolano e Ostia. Simili strumenti sono sovente raffigurati, per lo più in grandezza reale, in rilievi funebri di artigiani, tra cui il monumento di T. Statilius Aper, quello di Aebutius e il Lapis Capponianus, tutti ai Musei Capitolini di Roma; la stele funeraria di P. Celerius Amandus presso il Cardo Maximus di Ostia; un sarcofago nelle catacombe di Pretestato (III sec. d.C.) e alcune pitture delle catacombe di S. Agnese (IV sec. d.C.), ora nel Palazzo dei Conservatori a Roma. Non mancano rappresentazioni di simili strumenti su monumenti di altro tipo, come sull'arco di Traiano a Benevento. Secondo le fonti antiche (Vitr., X, 9, 1), inoltre, esisteva uno strumento, l'odometro (di cui non è però pervenuta finora alcuna documentazione archeologica), che consentiva di misurare la distanza percorsa durante un viaggio in carrozza, e che quindi doveva avere la sua utilità nella redazione di carte e itineraria.
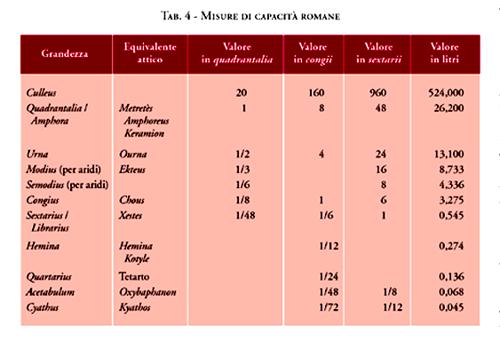
Misure e campioni di capacità
L'uso di misure di capacità locali in ambito italico è attestato solo sporadicamente. Su alcuni contenitori per derrate lucani (soprattutto da Buccino) sono iscritte delle misure che fanno riferimento a standard non romani. Le cavità della mensa mensuraria rinvenuta nel foro di Pompei, su cui al momento della scoperta si poteva ancora leggere l'originaria scritta in osco Kuinikis, erano state allargate in età augustea per adeguarle alle capacità romane. Nella villa di Boscoreale sono stati rinvenuti gli elementi bronzei di un modius campione, la cui capacità ricostruita (20,555 l) equivarrebbe al cubo di un piede osco. Il sistema di misure di capacità romano è fortemente influenzato da quello attico, che in età ellenistica è ormai organizzato secondo le regole di un sistema "chiuso"; le tracce di tale adattamento sono chiaramente individuabili. L'unità teorica fondamentale è il quadrantal o amphora, corrispondente ad uno dei valori possibili dell'amphoreus attico, di volume pari al cubo del piede di 29,6 cm, cioè a 26,2 l, e di peso in acqua di 80 libbre, così come stabilito dal Plebiscito Silio nel III sec. a.C. Di fatto, l'unità d'uso più comune è il sextarius, originariamente detto librarius, che doveva essere l'unità di riferimento tradizionale equiparata alla libra, come attesta l'andamento duodecimale della serie dei suoi sottomultipli. L'atticizzazione si manifesta probabilmente nel cambiamento del nome, che pare indicare come unità d'uso il congius, equivalente alla chous. Del pari estranee all'andamento duodecimale sono le grandezze per misurare gli aridi, il modius (pari a 1/3 del quadrantal ) e il semodius (Tab. 4). La documentazione archeologica di campioni per le misure di capacità è piuttosto scarsa: un buon esempio è costituito dai due vasi cilindrici di bronzo (rispettivamente da 20 e 8 sextarii) del Museo Archeologico Nazionale di Napoli. Gli esemplari del Museo Nazionale Romano sono esposti ora nelle Terme di Diocleziano. Più ricca è la documentazione fornita dalle mensae mensurariae, a Minturno, a Ostia (dove ne sono state rinvenute quattro), a Pompei e a Tivoli. Il volume delle anfore da trasporto, classe da cui prende nome la misura fondamentale, sembra variare in relazione al contenuto. Per quanto è possibile stabilire, le anfore vinarie più diffuse tra I sec. a.C. e II sec. d.C. nel mondo romano hanno una capacità media di circa 1 quadrantal (Dressel 1 A e B, Dressel 2-4) o di poco superiore (Haltern 70). In seguito, tra la fine del I e il III sec. d.C., alcuni tipi, probabilmente vinari, coprono una gamma completa di dimensioni e capacità, dal formato di circa 2 congii, all'urna, al quadrantal e mezzo (Gauloise 12). Le anfore adibite al trasporto di olio o di pesce conservato tra I e IV sec. d.C. hanno una capacità media maggiore, pari o superiore ai 2 quadrantal (Dressel 20, Tripolitana, Africana grande). Le iscrizioni sui dolia (ca. 1500- 2000 l / 3-4 cullei ciascuno) rinvenuti in una serie di relitti databili tra la metà di I sec. a.C. e la metà del I sec. d.C. indicano chiaramente che la capacità era per lo più calcolata in anfore /quadrantalia.
Diffusione in ambito provinciale
Durante l'età imperiale, le misure romane si diffondono in tutte le province, il più delle volte accanto a quelle locali. Si determina anche un progressivo adattamento delle misure locali a quelle romane, soprattutto nell'ambito dei territori appartenuti a regni ellenistici, dove spesso le unità in uso erano già adattate a quelle attiche. Rimangono però forti particolarità, specialmente in Egitto, dove sopravvivono, anche con nome e adattamenti romani, misure tolemaiche ed egiziane di peso, di capacità, di lunghezza e di estensione. L'unità di superficie è l'arura. Il miglio è ragguagliato a 8 stadi, e corrisponde così a quello romano. Particolarità sono attestate anche in Siria e in Palestina. In ambito occidentale, la lega gallica è equiparata a 1 miglio romano, il pes Drusianus e l'hasta germanici rispettivamente a pes et sescuncia e a 3 miglia. Nelle province, insomma, tradizioni locali e usanze romane convivono ed è possibile riscontrare la presenza e l'impiego di diversi standard (soprattutto nell'ambito delle misure lineari) non solo nei monumenti, ma anche nelle mensae mensurariae, per facilitare la comparazione, come attestano vari ritrovamenti in Francia, Libia e Tunisia. La situazione metrologica delle province africane è piuttosto complessa: come misure lineari sono usati contemporaneamente il cubito punico structorius di 51,6 cm, il più facile da convertire in misure romane (4 cubiti equivalgono a 7 piedi romani) e quindi il più usato in costruzioni che prevedevano l'impiego di marmi pregiati tagliati in province lontane su misure attico-romane; il cubito punico fabrilis di 50,9 cm, appena più corto del precedente e di lunga tradizione artigianale locale; il cubito tolemaico di 52,5 cm; il piede romano. Su una stessa mensa proveniente dal mercato augusteo di Leptis Magna (Libia) sono incisi i modelli metrici per il cubito punico structorius, il piede romano e il cubito tolemaico. I maggiori edifici della città sono costruiti secondo due ordini di misure: il progetto e le partizioni architettoniche sono in piedi romani; i blocchi sono tagliati secondo il cubito punico fabrilis. Una breve rassegna delle altre città africane della Tunisia e della Libia (antica Africa Proconsularis) mostra come l'unità più usata sia il cubito punico structorius, impiegato sia in tipologie architettoniche di tradizione locale che in quelle di tradizione romana, ma che anche il piede romano è piuttosto frequente; in alcuni casi, le due misure coesistono. Tale molteplicità continua anche in età tardoantica, almeno fino a tutto il V sec. d.C. A Palmira (Siria) i principia dell'accampamento romano (300 d.C.) e molti altri edifici cittadini sono costruiti sulla base del piede romano, ma spesso i rifacimenti, i reimpieghi e le decorazioni sono attuati secondo altre misure. Le misure lineari romane trovano applicazione anche in Grecia, sia ad Atene (il Tempio di Roma e di Augusto sull'Acropoli, la Porta e la Biblioteca di Adriano, l'Orologio di Andronikos, l'Agoranomion) sia fuori (l'heroon a ovest del santuario di Delfi e l'arco di Caracalla a Taso). Ben si prestano all'analisi metrologica i resti degli impianti militari romani, concepiti spesso secondo piani prestabiliti e sulla scorta di una dettagliata manualistica. Sulla base delle istruzioni fornite da Polibio e da Igino (Mun. Castr.) è infatti possibile ricostruire la geometria ideale dei castra e ricercarne poi le diverse applicazioni sul terreno. L'esame di una serie di forti romani e di città che sorgono su antichi accampamenti sul suolo britannico ha messo in luce l'estrema variabilità degli impianti, tutti però basati su moduli multipli del piede romano. La diffusione delle misure romane nelle province è attestata anche dal ritrovamento di strumenti di misurazione tarati su standard romani. La centuriazione coloniale è tradotta su tavole marmoree, come quelle di Orange (Francia). Non manca una documentazione relativa ai modii, soprattutto nelle province occidentali (Spagna, Regno Unito); in oriente il modius è equiparato a unità locali. Regulae sono note, oltre che dall'Italia, da varie città di Francia e da Magdalensberg (Austria). Fanno sempre riferimento al piede attico-romano le regulae rappresentate in mano alle personificazioni di Ktisis ("costruzione") nei mosaici di Kourion (Cipro) e di Antiochia sull'Oronte (Turchia), e quella incisa sull'acquedotto nei pressi di Betlemme, accompagnata dall'iscrizione di Flavius Eneas Silentiarius: to de metron tou podos hypotetaktai toutois tois typois (la misura del piede segue questo modello).
Bibliografia
In generale sui sistemi metrici (di lunghezza, di capacità e di peso) e sulla loro documentazione archeologica:
A. Segré, Metrologia e circolazione monetaria degli antichi, Bologna 1928; Id., Pesi e misure, in V. Ussani - F. Arnaldi (edd.), Guida allo studio della civiltà romana antica, I, Napoli 1959, pp. 533-40; A. Stazio, Lineamenti di metrologia romana, ibid., pp. 541-45; M.H. Crawford, Coinage and Money under the Roman Republic. Italy and the Mediterranean Economy, London 1985; M. Cattani, Numeri, pesi e misure; il calcolo del tempo, in S. Settis (ed.), Civiltà dei Romani, III, Il rito e la vita privata, Milano 1990, pp. 115-23; D. Ahrens - R.C.A. Rottländer (edd.), Ordo et mensura. I. Interdisziplinärer Kongreß für Historische Metrologie vom 7 bis 10 September 1989 im Städtischen Museum Simeonstift Trier, III, St. Katharinen 1991; M. Cattani, s.v. Misura, in Enciclopedia Oraziana, II, Roma 1997, pp. 215-16; A. Ciarallo - E. De Carolis (edd.), Homo Faber. Natura, scienza e tecnica nell'antica Pompei (Catalogo della mostra), Milano 1999, pp. 152, 224-25, 281-85, nn. 153, 300-308, 314, 364-77, 380, 384, 387.
Misure di capacità delle anfore:
D.P.S. Peacock - D.F. Williams, Amphorae and the Roman Economy. An Introductory Guide, London - New York 1986, p. 52. Misure lineari: G. Ioppolo, La tavola delle unità di misura nel mercato augusteo di Leptis Magna, in QuadALibia, 5 (1967), pp. 89-98; Bauplanung und Bautheorie der Antike. Bericht über ein Kolloquium vom Architekturreferat des Deutschen Archäologischen Instituts mit Unterstützung der Stiftung Volkswagenwerk in Berlin vom 16.11. bis 18.11.1983, Berlin 1984; Le dessin d'architecture dans les sociétés antiques (Actes du Colloque de Strasbourg, 26-28 janvier 1984), Strasbourg 1985; D. Theodorescu, Le Forum et le temple "doriquecorinthien" de Paestum. Une expérience pre-vitruvienne, in H. Geertman - J.J. de Jong (edd.), Munus non ingratum. Proceedings of the International Symposium on Vitruvius' "De Architectura" (Leiden 20-23 January 1987), Leiden 1989, pp. 114-25; P. Barresi, Sopravvivenze dell'unità di misura punica e i suoi rapporti con il piede romano nell'Africa di età imperiale, in Africa Romana VIII, pp. 479-502; Id., Unità di misura nell'architettura dell'Africa tardoromana e bizantina, in Africa Romana IX, pp. 831-42; G. Ioppolo, Le Terme del Sarno a Pompei. Iter di un'analisi per la conoscenza, il restauro e la protezione sismica del monumento, Roma 1992, pp. 109-18; Ph. Crummy, Metrological Analysis of Roman Fortresses and Towns in Britain, in S.J. Greep, Roman Towns: the Wheeler Inheritance. A Review of 50 Years' Research, York 1993, pp. 111-19; J.-P. Adam, Le temple de Portunus au Forum Boarium, Rome 1994.
Sistemi ponderali
di Maria Emanuela Alberti
Le fasi formative dei sistemi metrici in uso nella penisola italiana in età storica sono in genere di difficile definizione: solo per quelli ponderali è possibile disporre di alcune informazioni dirette e indirette. Ciononostante, le realtà ponderali in ambito non romano o non romanizzato sfuggono quasi completamente. Il sistema ponderale romano nella sua formulazione tardorepubblicana è più conservativo rispetto a quello lineare e a quello di capacità, con strutture di computo ancorate al sistema di calcolo originario. In età imperiale e poi tardoantica il sistema subisce alcuni cambiamenti, a causa del legame diretto tra misure di peso e standard monetali, modificati a più riprese per le vicissitudini economiche dell'Impero.
Le origini
Per quanto riguarda il periodo compreso tra il VI e il IV sec. a.C., la documentazione dei primi scambi in metallo in ambito italico non consente la definizione di norme precise. Né i materiali dei ripostigli, né le forme di metallo fuso circolanti nell'Italia centro-settentrionale (aes rude e lingotti, spesso contrassegnati con il tipo del "ramo secco") sembrano seguire alcun riferimento ponderale. A Roma un'unità di metallo pesato, che prende il nome dalla libbra (libra, esito parallelo al greco litra), sarebbe stata impiegata nel corso del V sec. a.C. per quantificare e pagare le ammende e gli indennizzi. Nel IV sec. a.C., con l'inizio della monetazione librale in bronzo fuso a Roma e nei centri sotto la sua influenza (aes grave), l'unità monetaria è l'asse (as), del valore di una libbra. Anche se il diffondersi di tale monetazione segue con ogni probabilità l'impulso di Roma, le emissioni dei singoli centri sembrano riflettere tradizioni locali. L'area tirrenica (Etruria, Lazio, Umbria interna, fino alla Sicilia) è caratterizzata dall'uso di un sistema di frazionamento duodecimale, quella adriatica (dall'Umbria all'Apulia) da un sistema decimale. Il valore stesso della libbra si differenzia da centro a centro, anche in funzione del periodo e delle alleanze politiche. I contemporanei lingotti di bronzo fuso contrassegnati, o aes signatum (IV-III sec. a.C.), emessi a Roma a fianco della moneta, hanno un valore ponderale definito di circa 5 libbre. In area osca e umbra, l'unità di monetazione usata non è l'asse, ma il nummus, termine di chiara derivazione greca, probabilmente designante in origine un'unità di bronzo pesato.
Mondo etrusco-italico
Nell'ambito delle misure di peso, il panorama delle testimonianze note per il mondo italico non romano o non romanizzato è alquanto deludente, se si prescinde delle emissioni di bronzo librale. Una documentazione ponderale cospicua, purtroppo sprovvista di dati precisi su contesto e cronologia, è quella della città etrusca padana di Marzabotto. I pesi che vi sono stati rinvenuti sono ciottoli fluviali, levigati artificialmente per consentire un più facile appoggio sui piatti della bilancia e per aggiustare il peso. I numerosi segni incisi, spesso numerali, fanno riferimento a un sistema di frazionamento decimale. La principale unità di peso individuata, di 370-379 g, è comparabile con l'unità dell'aes grave emesso in ambito adriatico o italico-orientale, vicina a quella romana ma divisa su base decimale, mentre non trova paragoni con l'aes grave noto per l'Etruria propria.
Mondo romano
Fin dalle prime attestazioni, l'unità di misura di peso fondamentale in ambito romano e italico è dunque la libra, detta anche pondus, cui viene equiparato l'asse monetale. In età repubblicana, probabilmente già nell'età dei decemviri, nell'adeguamento al sistema attico un talento di 26,2 kg viene ragguagliato a 80 libbre (Liv., XXXVIII, 38, 13), per un valore teorico della libbra di 327,45 g. Di fatto, tale valore oscilla tra 327,5 g e 323,5 g a seconda del dato diretto (pesi rinvenuti) o indiretto (equiparazione con misure greche, attiche e alessandrine). Proprio la mancata corrispondenza 1:1 tra le misure della libbra e del talento, e ancor di più tra la libbra e il peso in acqua della maggiore unità di capacità romana, il quadrantal (equivalente al talento e quindi a 80 libbre), è il segno del persistere di radicate tradizioni metrologiche locali all'interno di un sistema atticizzato. L'intero sistema librale, nella denominazione delle grandezze e nel sistema di frazionamento duodecimale, sfugge all'equiparazione con i nominali greci; la laboriosità del calcolo per passare da un sistema di conto duodecimale a uno decimale è testimoniata anche dalla letteratura (Hor., Ars, 325-26). In ambito monetale, il sistema di divisione decimale attico è adottato per i valori del denarius, per necessità di commercio e scambio con l'intero mondo ellenistico. Se i sottomultipli della libbra seguono un sistema duodecimale (12 once, ciascuna di 24 scrupula), i suoi multipli seguono quello decimale, fino al centumpondium (Tab. 1). In età imperiale vengono compiuti ulteriori passi per l'adeguamento del sistema di conto romano a quello attico: la dracma, equiparata al denario neroniano di 3 scrupula, è inserita tra le frazioni della libbra. Le modifiche più importanti però fanno seguito alla riforma monetale costantiniana del 307 d.C.: il solidus aureus diventa unità di peso, col nome di solidus in occidente e di nomisma in oriente; corrisponde a 1/72 di libbra, che ha pertanto subito una riduzione a 326,6 g teorici. In relazione alla medesima riforma, viene inoltre introdotta la divisione in lupini e siliquae (gr. keratia) e vengono creati dei pesi monetali, gli exagia solidi, destinati al controllo delle nuove emissioni e provvisti di indicazioni cronologiche (nomi o monogrammi imperiali, nomi di funzionari). Nel 363 d.C. Giuliano stabilisce che siano posseduti e usati solo dai fabbricanti di pesi ufficiali. Sempre a partire dall'inizio del IV sec. d.C., inoltre, i pesi sono tagliati sia su base librale che su base onciale. In età tardoantica, la libbra continua a subire un calo progressivo, fino a pesare 324 g tra il IV e il VI sec. d.C., con un'oncia di 26,667 g (Tab. 2). Nel mondo romano, la pesatura avviene con due tipi di bilance, restituite in gran numero dall'indagine archeologica: la bilancia a due piatti (trutina o libra) e la stadera, in genere a più portate (statera, trutina campana). La prima era usata da tempo nel bacino del Mediterraneo; la seconda, che con ogni probabilità era già nota in ambiente campano in età ellenistica, è il tipo più comune in età romana, quando conosce un'applicazione pratica su larga scala; ancora oggi è molto diffusa. Per quanto riguarda le trutinae, in età romana e bizantina si realizzano esemplari da trasporto con l'asse pieghevole, nonché alcuni tipi speciali: bilance di piccole dimensioni per la pesatura di determinate monete, con un piatto più pesante dell'altro (trutina momentana o moneta), e bilance molto grandi, per carichi grossi che richiedevano la stabilità dello strumento (si veda, ad es., il rilievo sul sepolcro di Eurisace presso Porta Maggiore a Roma). Ci sono poi numerose attestazioni di tipi intermedi tra la trutina e la statera: bilance a due piatti dotate di scala graduata e peso cursore. Per utilizzare la trutina, vengono impiegati pesi da bilancia veri e propri: essi hanno spesso una forma sferoidale o ellissoide con le due basi piatte, non sono forati, e sono realizzati in pietra o in metallo (piombo o bronzo). Per la pesatura dei carichi maggiori, si usano pesi litici a forma di tronco di cono su base ellissoidale, generalmente molto pesanti. Non mancano però esemplari di altra forma, anche figurata. Comune è anche la presenza di una maniglia per la presa. In alcuni casi, è possibile rilevare tracce dell'aggiustamento della massa: i pesi più leggeri (unciali) sono massicci e si agisce ritoccando il manubrio o asportando materia; quelli più pesanti (librali) sono vuoti internamente e la taratura avviene con materiale di riempimento (sabbia, piombo, ferro). I pesi sono spesso contrassegnati con sigle, numerali e puntini. I pesi campione sono ageminati. In età tardoantica, a partire dal IV sec. d.C. fino all'età giustinianea, in Oriente sono utilizzate correntemente, al posto dei numerali, le lettere dell'alfabeto greco. Allo stesso periodo risale l'introduzione di simboli speciali per l'oncia e per la libbra, nonché la rinnovata popolarità del peso di piombo quadrangolare, con le sigle ageminate, che soppianterà ben presto il tipo sferoidale a basi piatte, attestato per l'ultima volta sotto Giustiniano. Per la stadera, invece, non si usano tanto dei veri e propri pesi, quanto dei contrappesi: gli aequipondia hanno un anello di sospensione e sono realizzati in bronzo con le forme più svariate. Bilance, stadere e pesi venivano controllati alla fabbricazione (o anche in circolazione) per mezzo di campioni conservati presso templi (a Roma, presso il Tempio di Giove Capitolino e quello dei Castori) o alcuni edifici pubblici. Tale controllo era pertinenza degli edili in età repubblicana (Cic., Epist., 8,6,4; Digesta Iustiniani Augusti, 19, 2, 13, 8) e del praefectus urbi in età imperiale (almeno dal II sec. d.C.). Non mancano iscrizioni su bilance e pesi che attestano l'avvenuto controllo (CIL III, 12645; V, 8118, 4; X, 8067, 3; X, 8068 a-d; X, 28067, 2; XI, 6727, 1). L'attenzione governativa verso l'affidabilità di pesi e monete è costante, soprattutto in età tardoantica: nel 363 d.C., Giuliano crea dei nuovi magistrati, gli zygostates, provvisti di pesi garantiti dallo Stato e di bilance ben calibrate, disposti in tutte le città dell'Impero per controllare il commercio dell'oro e scoraggiare la tosatura delle monete. Nel Tardo Impero il compito di sorvegliare pesi e misure è affidato, a seconda dei tempi e dei luoghi, al praefectus urbi, al proconsul, al comes sacrarum largitionum. La documentazione archeologica dei vari tipi di pesi e bilance romani è ricchissima, rinvenuta soprattutto nella zona di Roma e nelle rovine di Ercolano e Pompei, dove molte bilance sono state trovate in casa di medici, farmacisti, vasai, orafi e commercianti. Cospicua è anche la documentazione dell'Italia settentrionale, ad esempio del territorio di Adria, di Aquileia e di Bolzano.
Diffusione in ambito provinciale
Come per le misure di capacità e di lunghezza, nelle province sistemi ponderali di tradizione locale coesistevano con quello romano: in Egitto, ad esempio, la libra era di 349,3 g. La documentazione di pesi e bilance romane nelle province dell'impero è pure cospicua: pesi per trutina e aequipondia sono stati rinvenuti, tra l'altro, nell'Agorà di Atene, a Treviri, a Gerusalemme; bilance e stadere provengono da numerosi relitti d'età romana in tutto il Mediterraneo. Per quanto riguarda il commercio dei metalli, il centumpondium è il valore teorico dei lingotti di piombo betico (Spagna) fusi tra I sec. a.C. e I sec. d.C.: i numerali che vi sono iscritti indicano il numero di libbre in esubero rispetto a tale massa. Di gran lunga meno standardizzata risulta la produzione di lingotti di rame.
Bibliografia
Per le misure e gli strumenti ponderali:
M. Lang - M. Crosby, Weights, Measures and Tokens. The Athenian Agora. X. Results of Excavations Conducted by the American School of Classical Studies at Athens, Princeton 1964; B. Kisch, Scales and Weights. A Historical Outline, New Haven - London 1969; P. Lopreato, I pesi ageminati del Museo di Aquileia e il sistema ponderale bizantino, in I Musei di Aquileia. Arti applicate - ceramica - epigrafia - numismatica, in Antichità Altoadriatiche, 14 (1984), pp. 71-102; R. Bussi - V. Vandelli (edd.), Misurare la terra: centuriazione e coloni nel mondo romano. Città, agricoltura, commercio: materiali da Roma e dal suburbio, Modena 1985, pp. 23-61, 208-223; E. Cavada et al., Lineamenti di metrologia antica: stadere e bilance romane nel Trentino, in Archeologia delle Alpi, 2 (1993), pp. 83-127; M. Cattani, Il sistema ponderale di Marzabotto, in AnnIstItNum, 42 (1995), pp. 21-79.
Per il bronzo librale:
R. De Marinis (ed.), Gli Etruschi a Nord del Po, I, Udine 1988, pp. 201-210; F. Panvini Rosati, Aes signatum. Un aspetto dell'economia nell'Emilia preromana (Catalogo della mostra), Reggio Emilia 1988; N.F. Parise, Libbre e bronzo librale nell'Italia antica, in G. Pugliese Carratelli (ed.) Italia omnium terrarum parens. La civiltà degli Enotri, Choni, Ausoni, Sanniti, Lucani, Brettii, Sicani, Siculi, Elimi, Milano 1989, pp. 581-99.
Per i lingotti:
B. Liou - C. Domergue, Le commerce de la Bétique au Ier siècle de notre ère. L'épave Sud-Lavezzi 2 (Bonifacio, Corse Sud), in Archaeonautica, 10 (1990), pp. 11-124.
Periodo tardoantico e medievale
di Paolo Güll
I sistemi di misura lineari, ponderali e di capacità
Le linee di sviluppo della metrologia medievale vanno tracciate a partire da due grandi quadri di riferimento: da un lato il mondo tardoantico, luogo di una sostanziale uniformità metrologica e, all'opposto, la frammentazione caratteristica del Basso Medioevo, efficacemente dipinta da molte fonti, tra tutte le pratiche di mercatura. In quest'ambito, le conoscenze in materia incontrano ostacoli rilevanti proprio nel cercare di comprendere il modo con cui il sistema romano si sia sfaldato, lasciando tuttavia tracce evidenti in tutto il Mediterraneo, e soprattutto le cause di questa trasformazione. Gli studi risentono significativamente di questa bipartizione. La bibliografia sul mondo tardomedievale è numerosa e di facile reperibilità: per l'Italia, è opportuno segnalare il repertorio di R.E. Zupko (1981), che sistematizza, nei limiti obbligati della ricostruzione storica, le principali conoscenze sulla metrologia dall'XI secolo in poi, corredate da numerosi esempi desunti dalle fonti scritte più significative, equivalenze e rapporti tra unità di misura; per l'Alto Medioevo, invece, l'analisi dei mutamenti che investono il sistema metrologico romano è fondata su un dossier costituito principalmente da ipotesi, anche se spesso ben fondate, specie quando si cerchi la causa originante di queste trasformazioni. Sono state chiamate in causa a tale proposito varie eventualità, in cui differenti apporti avrebbero contribuito a modificare in modo sostanziale equivalenze e rapporti interni del sistema romano, ma nessuna sembra finora totalmente convincente, o, meglio, nessuna sembra aver agito in modo autonomo.
Tarda antichità e alto medioevo
Sembra accertato che, come accade per molti altri aspetti dell'organizzazione sociale, il sistema metrologico romano sia sopravvissuto in molte zone del Mediterraneo fino all'VIII secolo: nei territori bizantini ancora nel pieno VI secolo si utilizzava, per la misura delle superfici, uno iugero di 2520 m² e i primi denari di Carlo Magno risultano coniati a partire da una libbra di circa 327 g: si tratta dunque ancora dei valori in uso in età imperiale. Anche se alcune unità di misura di tradizione preromana, mai abbandonate dalle popolazioni locali, possono aver influito su modificazioni metrologiche anche significative, resta il fatto che da un punto di vista concettuale il sistema romano continua a prevalere; ciò avviene infatti sia da un punto di vista linguistico (i nomi che identificano le varie unità di misura sono e restano quelli latini), sia, ciò che è più importante, da quello dei rapporti interni fra le diverse misure, che continuano in larga parte ad obbedire alla logica duodecimale del sistema metrico classico. A questo stadio, alcuni elementi sono di difficile inquadramento e nascondono questioni più complesse, ad esempio il problema dell'equivalenza geometrica di quelle unità di grandezza "naturale" che hanno come origine la misura della quantità di semenza. Non sempre questa misura viene fissata in un valore geometrico, come però sembra accadere al modius, unità di misura del volume di semenza che fissa il proprio valore geometrico attorno ad 1/3 di iugero. Un primo mutamento significativo sarebbe avvenuto, almeno in Italia, nella prima metà dell'VIII secolo, con l'introduzione del cosiddetto "piede liprando" o piede di Liutprando, una misura lineare di supposta origine longobarda che corrisponderebbe a 1,5 piedi romani. Questa unità di misura ha un suo multiplo, la pertica di 12 piedi liprandi, cioè 18 piedi romani. Pur nella variazione metrologica che potrebbe avere realmente una sua origine in una misura in uso presso le popolazioni germaniche, la logica duodecimale del sistema romano continua, come si vede, a prevalere. Per alcuni autori, inoltre, questa variazione del valore del piede sarebbe all'origine dell'abbandono nei documenti dell'indicazione della superficie dei lotti di terra, dato che le vecchie misure contenute nella documentazione anteriore sarebbero in tal modo divenute prive di significato.
Età carolingia - Si deve a Carlo Magno una fondamentale riforma del sistema metrico, oggetto di vastissima bibliografia da parte degli studiosi di numismatica per quanto riguarda le unità di misura ponderale: per la storia della monetazione europea, infatti, il passaggio dalla libbra di 326 g a quella di 408 g, valore per il quale c'è maggiore unanimità tra gli studiosi, riveste un'importanza capitale. Tuttavia, le cause che vengono invocate per questa trasformazione sono molto diverse, spesso basate su pure ipotesi metrologiche. Inizialmente era stata evocata un'influenza del marco, un'unità ponderale di origine germanica: in questa tesi viene assunto un valore di 0,0637 g per il grano (la ventiquattresima parte di un denaro) sulla base del quale si ottiene un valore della libbra di circa 367 g in rapporto di 9 a 8 con la libbra romana di 326 g. Supponendo anche il passaggio da una divisione in 8 once ad una in 12, si ottiene un valore finale per la libbra carolingia di 489 g (questo secondo valore in realtà non più accettato dagli studiosi). Un'altra ipotesi chiama in causa un'influenza araba: partendo dal valore più plausibile di 408 g per la libbra carolingia, calcolando che 30 denari d'argento del peso di 1,701 g (tagliati appunto in una libbra di 408 g), cioè un mancus, corrispondono a 51,03 g d'argento, e dividendo questo valore per 12 (che rappresenta il rapporto di cambio tra oro e argento nel sistema carolingio), si ottiene il peso in oro di 4,2525 g, corrispondenti al dīnār arabo. La libbra romana di 326 g e questa libbra carolingia di 408 g sono inoltre in rapporto 12 a 15, cosa che ha fatto pensare al passaggio da una libbra di 12 a una di 15 once. L'attività normativa di Carlo Magno, però, non trascurò le misure di capacità, stanti le numerose indicazioni delle fonti, e neanche quelle di superficie, molte delle quali sono, come si è detto, tradizionalmente connesse alle prime. Sono stati fatti vari calcoli per stabilire l'equivalenza del moggio, ma nessuno sembra allo stato attuale soddisfacente, per gli scarsissimi elementi su cui questi computi si fondano. Un dato invece certo, su cui le fonti scritte sono unanimi, è l'esistenza di una volontà di controllo sulle unità di misura, che testimonia il tentativo da parte del potere centrale di assumere una reale funzione di controllo in questo campo: numerosi capitolari carolingi sottolineano la necessità di avere "aequales mensuris et recta et pondera iusta et aequalia (...) sive ad dandum in illis sive ad accipiendium". In particolar modo le relazioni dei vescovi all'imperatore si soffermano sulle conseguenze della mancata osservanza di tali disposizioni che colpirebbe specialmente i più poveri.
Pieno e basso medioevo
È solo verso la fine del X secolo che si manifestano pienamente i fenomeni di frammentazione metrologica, specialmente in Europa meridionale ed in particolare in Italia, dove il fenomeno diventerà particolarmente avvertibile anche per la forte parcellizzazione dei poteri locali. La documentazione scritta e la bibliografia che ne deriva sono per questa epoca molto più ricche ed aumentano in modo esponenziale a mano a mano che ci si addentra nel Basso Medioevo: del resto, gran parte delle fonti rientrano nelle categorie maggiormente utilizzate dagli storici dell'economia, per i quali i dati in grande serie acquistano senso solo se convertiti in unità di misura da noi utilizzabili. L'impalcatura linguistica dei sistemi bassomedievali, che saranno poi ereditati da quelli metrici predecimali di epoca moderna, resta ancora quella latina. Si osserva, però, l'introduzione di alcune unità di misura di origine araba alcune delle quali denunciano anch'esse una precedente origine latina. Il caso di un'unità di peso, il qinṭār, da cui cantarus, termine che proviene da centenarius (ed infatti corrisponde a 100 raṭl ), pare significativo in questo senso; tuttavia, altre unità come il rubbio (rub'a), una misura di capacità per liquidi e aridi ed anche di superficie della terra, il caffiso (qafīz), unità di misura per liquidi, ed il carato (qīrāt, fagiolo), unità di peso, denunciano un apporto reciproco, conseguenza della ormai complessa articolazione del commercio col Levante. Similmente, anche nel mondo bizantino molte unità di misura, specialmente quelle non ufficiali, testimoniano meccanismi simili, di cui le pratiche di mercatura danno ragione, ed apporti in entrambe le direzioni. Se l'influenza del sistema romano continua ad essere evidente soprattutto nell'origine dei termini, in quest'epoca si verifica invece una innovazione sostanziale nel rapporto fra le differenti unità di misura, e cioè il passaggio da un sistema duodecimale (che pure non verrà mai completamente abbandonato fino all'avvento del sistema metrico decimale) ad un sistema definito "a base 2". Nelle misure per liquidi, ad esempio, i tipici rapporti metrologici nel Basso Medioevo sono rappresentati dal boccale che equivale a due mezzi, che equivalgono a loro volta a quattro fogliette, ed analogamente per i multipli fino alle capacità maggiori come la botte: in questo sistema, dunque, molte unità equivalgono al doppio o alla metà di un'altra. A questo proposito è impossibile entrare nel dettaglio delle varie equivalenze con le misure moderne, per le quali da un lato si può rinviare ai numerosi repertori e dall'altro va ricordata l'esistenza di numerosi campioni conservati dalle magistrature comunali in diverse città ed ancor oggi visibili; è però da sottolineare ancora una volta l'estrema variabilità delle stesse, fenomeno di anarchia metrologica per cui non esistono spiegazioni completamente convincenti. Si può osservare una tendenza di massima all'aumento del valore di ciascuna unità espresso in misure attuali e questo fenomeno potrebbe suffragare le due principali teorie che sono state formulate nelle quali si ipotizza una progressiva manipolazione dei campioni delle varie unità per consentire o un aumento surrettizio della pressione fiscale o un maggiore sfruttamento della manodopera. Tuttavia queste interpretazioni si scontrano con la frequente evidenza di unità di misura che riducono anche sensibilmente il proprio valore.
Bibliografia
Repertori generali di equivalenze tra i sistemi predecimali ed il sistema moderno:
J.-J. Bourgeois, Nouveau manuel des poids et mesures, Paris 1879; A. Martini, Manuale di metrologia, Torino 1883; F.W. Clarke, Weights, Measures and Money of All Nations, New York 1988.
Per le pratiche di mercatura:
F. Balducci Pegolotti - A. Evans, La pratica della mercatura, Cambridge (Mass.) 1936; A. Borlandi, Il manuale di mercatura di Saminiato de' Ricci, Genova 1963; C. Ciano, La "pratica di mercatura" datiniana (secolo XIV), Milano 1964; B. Dini, Una pratica di mercatura in formazione (1394-1395), Firenze 1980.
Per un repertorio di unità di misura a partire dai secoli centrali del Medioevo italiano:
U. Tucci, Pesi e misure nella storia della società, in Storia d'Italia. V, I documenti, Torino 1973, pp. 581-612; R.E. Zupko, Italian Weights and Measures from the Middle Ages to the Nineteenth Century, Philadelphia 1981.
Studi di base sulla metrologia:
W. Kula, Les mesures et les hommes, Paris 1984; R.E. Zupko, Revolution in Measurement: Western European Weights and Measures since the Age of Science, Philadelphia 1990; Id., s.v. Metrologia architettonica, in EAM, VIII, 1997, pp. 354-57.
Sul passaggio dalla Tarda Antichità all'Alto Medioevo:
H.A. Miskimin, Two Reforms of Charlemagne? Weights and Measures in the Middle Ages, in EconHistR, ser. 2, 20 (1967), pp. 35-52; A. Chiavari, Misure agrimensorie altomedievali dell'Italia centrale. Il piede di Liutprando ed il moggio nell'area marchigiana nei secoli VIII-XII, in Atti e Memorie della Deputazione di Storia Patria per le Marche, 86 (1981), pp. 895-953; H. Witthöft, Thesen zu einer karolingischen Metrologie, in P.L. Butzer - D. Lohrtnann (edd.), Science in Western and Eastern Civilization in Carolingian Times, Basel - Boston - Berlin 1993, pp. 503-24.
Per la metrologia carolingia:
Ph. Grierson, Carolingian Europe and the Arabs: the Myth of the "mancus", in RBelgPhilHist, 32 (1954), pp. 1059-1075; P. Portet, Remarques sur les systèmes métrologiques carolingiens, in Le Moyen Âge, 97/1 (1991), pp. 5-24.
Mondo bizantino
di Daniele Castrizio
Sistemi ponderali
In linea generale, il sistema di pesi e misure in vigore nell'ambito dell'impero bizantino era ancora lo stesso usato in quello romano. Non è però facile determinare, trattandosi di un arco temporale molto ampio e di un altrettanto vasto ambito territoriale, se tale sistema sia stato modificato su base regionale (anche se sembra naturale che ciò sia avvenuto, almeno in parte) o se, nel corso dei secoli, i pesi siano stati, più o meno inconsapevolmente, mutati. La questione riguardante più specificamente i pesi è ulteriormente complicata dalle evidenti difformità che si notano nell'ambito del campione degli esemplari originali pervenutici. Ciò ha portato gli studiosi a risultati divergenti: se Th. Mommsen calcolava il peso teorico della libbra romana (in greco litra) in 327,45 g, sulla base della ricca collezione di pesi bizantini del Museo di Ginevra, N. Durr perveniva ad una libbra di 348 g, calcolata sulla media ponderale dei reperti. Usando lo stesso sistema, il catalogatore di una vendita d'asta del Munz Zentrum, avendo un altrettanto nutrito campione statistico, perveniva ad un dato difforme: 344 g. E. Schillbach, in un ampio lavoro di sintesi, ha calcolato una litra di 313-322 g come quella ufficiale nell'ambito dell'impero nel corso dei secoli VI e VII, ma credette di potere identificare anche una contemporanea libbra "provinciale" di circa 285 g. Un importante contributo viene dai pesi del relitto di Yassi Ada, studiati da K. Sams: dai reperti lo studioso riconobbe l'esistenza di una libbra di 284 g, mentre tutti i sottomultipli si attestavano su pesi sostanzialmente inferiori a quelli teorici. Lo studioso si spinse oltre, ipotizzando la presenza contemporanea di altri due sistemi ponderali, uno in cui la libbra si dividesse in 14 invece che in 12 once ed un altro in cui ogni oncia contenesse 7 solidi invece che 6. Nella pubblicazione dei pesi del Museo Numismatico di Atene, A.N. Oikonomides ha offerto un quadro d'insieme del problema da cui emerge chiaro come almeno il 30% dei pesi da una libbra si situi tra 325 e 315 g. Non solo, la studiosa greca ha notato come i pesi più piccoli divergano dallo standard ponderale in misura più consistente rispetto a quelli più grandi, che mostrano una variazione dalla misura teorica meno netta. Tirando le somme, esistette in epoca bizantina, come del resto anche precedentemente, una scarsa accuratezza nella realizzazione dei pesi, con valori spesso inferiori o addirittura superiori alla norma teorica. Come ha notato M. Hendy, è difficile arrivare a calcolare con certezza quanto le antiche misure ponderali abbiano perso del loro peso originario: ciò è tanto più vero ove si consideri che spesso gli stathmia e gli exagia erano ricoperti in argento o in altro metallo più o meno prezioso, oggi di solito completamente scomparso. Solo nei pesi di pietra e di vetro (in questo caso sempre pesi di monete, exagia) la perdita ponderale sembra essere stata di minore entità. Lo studioso ha rilevato anche come altri due fattori impedissero una precisione assoluta: i limiti fisiologici delle bilance medievali di essere accurate nel pesare e l'impossibilità a mantenere stabile un peso in un grande impero per la durata di molti secoli. Questa situazione si rispecchia nelle fonti, con molte leggi tendenti a disciplinare i pesi adottati nelle transazioni e a punire coloro che usavano misure ponderali appositamente falsate, evidentemente presenti in larga misura. Gli studiosi moderni non sono riusciti a pervenire al peso teorico della libbra nemmeno tramite la pesatura degli esemplari monetali, pur essendo noto che da una litra di metallo prezioso si dovessero battere 72 nomismata. Un altro sistema per accertare il peso reale della libbra si è basato su alcuni documenti del XIV secolo, in cui l'imperatrice reggente Anna di Savoia, vendendo a commercianti veneziani i gioielli della Corona, stabilì che si dovessero pesare ad pondus Constantinopolis e ad pondus Venetiarum. L'incrocio di questi due pesi, di cui quello veneziano noto, ha dato la sicurezza che a quella data la litra bizantina pesasse 304,13 g. Nonostante questa fonte, lo Hendy ha dimostrato che tale peso non rappresenta la vera misura della libbra bizantina dei tempi di Giustiniano I, ma che la litra romana è decaduta dal IX e poi ancora di più dal XIII secolo. Tutte queste considerazioni hanno portato la maggioranza degli studiosi ad assumere per la litra romana il peso teorico di 327,45 g ‒ o di 324/5 g circa ‒ come base del sistema ponderale, da cui anche quella bizantina strettamente discende. I pesi giunti sino a noi si possono dividere in due categorie: pesi commerciali (stathmia) e pesi di monete d'oro (exagia). Nei primi il sistema adottato è quello della libbra o litra, abbreviata con la lettera A, divisa in 12 once, ciascuna indicata come " " o "Γ", iniziali rispettivamente delle parole ΟΥΓΓΙΑ e ΓΟΥΓΓΙΑ. Gli exagia, invece, indicano il loro peso in nomismata o solidi, abbreviati in Oriente con la lettera N, in Occidente con la sigla SOL. Per quanto attiene alle misure attestate, senza entrare in dettagli, basti ricordare che ciascuna libbra di 12 once si componeva di 288 scripula o grammata. Tra i pesi commerciali erano usati, oltre la libbra, anche il semis (abbreviato "♉ G" o "Γ S"), il triens ("IIII", "♉ Δ" o "Γ Δ"), il quadrans ("III", "♉ Δ" o "Γ Γ"), il sextans ("II" o "♉ B" o "Γ B"), l'oncia ("I", " A" o "Γ A"), la semuncia ("XII" o "IB" = 12 scripula), la binae sextulae (1/3 di oncia), il sicilius (1/4 di oncia) e la sextula (1/6 di oncia). La libbra di solidi comprendeva 72 nomismata ("N OB" = nomismata 72), mentre il solidus ("SOL I" o "N") era diviso, a sua volta, in 24 siliquae o keratia. Attestati anche pesi di 12 keratia ("IB") e 8 keratia ("H" o "T"). Dai documenti pervenutici sappiamo che il primo a creare pesi per solidi (exagia) fu l'imperatore Giuliano nel 363, obbligando per legge ogni città ad avere uno zygostates, un pesatore ufficiale di monete. Una legge di Valentiniano II, Teodosio I e Arcadio, seguendo una norma similare di Graziano, Valentiniano II e Teodosio I, dà istruzioni al prefetto al Pretorio di assicurare che ogni città, e persino ogni stazione di cambio, abbiano una dotazione ufficiale di pesi e misure ( pondera, modii di bronzo o pietra, sextarii per i liquidi), perché ogni cittadino fosse sicuro, pagando le tasse, di avere sborsato il loro esatto ammontare. Un'altra normativa di Giustiniano, del 545, dava istruzione affinché i cittadini potessero ricevere dal prefetto i corretti pesi e misure, e dal comes sacrarum largitionum i pesi per i metalli preziosi. Tali pesi dovevano essere conservati presso la più importante chiesa di ciascuna città. Per quanto concerne l'Italia, Giustiniano stabilì che ogni versamento o ricevuta in beni o denaro dovesse essere regolata con pesi e misure stabilite alla presenza del papa di Roma e del senato della città. Il ruolo della Chiesa in tale campo viene ad essere confermato da un editto (prostagma) del neo consacrato patriarca di Antiochia Giovanni l'Elemosiniere, in cui l'uso di pesi e misure, non conformi a quelli legali, è vietato categoricamente. Nel 1107 un'ulteriore serie di documenti ufficiali attesta che nel tempio di S. Acindino a Costantinopoli erano conservati pesi e misure e che si pagava una tassa per poterli utilizzare. Una tale prassi è nota per altre chiese, anche con tariffe differenziate, spesso diversificate a seconda che si trattasse di stranieri o di residenti. Un accenno merita, infine, l'uso non legale di pesi e misure non bizantini, spia degli intensi rapporti con mercanti stranieri: in una chiesa di Costantinopoli era custodito un rubus ‒ un peso non ufficiale, forse di origine araba ‒ molto usato nell'ambito delle transazioni commerciali dell'intero Mediterraneo, posto a disposizione dei commercianti bizantini ed occidentali.
Bibliografia
J. Sabatier - J. Sabatier, Description générale des monnaies byzantines, frappées sous l'empereur d'orient depuis Arcadius jusqu'à la prise de Constantinople par Mahomet II, Paris - London 1862; G. Schlumberger, Mélanges d'Archéologie Byzantine, Paris 1895; U. Monneret de Villard, Exagia Bizantina in vetro, in RItNum, 5 (1922); N. Durr, Catalogue des poids Byzantines, Genève 1964; E. Schillbach, Byzantinische Metrologie, München 1970; W.M.F. Petrie, Glass Stamps and Weights. Ancient Weights and Measures, Warminster 1976; G. Bass - F. van Doorninck Jr., Yassi Ada, College Station 1982; M.F. Hendy, Studies in the Byzantine Monetary Economy c. 300-1450, Cambridge 1985; C. Morrisson et al., L'or monnayé. Purification et altérations de Rome à Byzance, in Cahiers Ernest-Babelon 2, Paris 1985. pp. 113-70; S. Bendall, Byzantine Weights. An Introduction, London 1996; Cataloghi d'asta: Munz Zentrum, Auctions XXXIII (23/11/1978); XXXVII (8/11/1979); XLV (2/11/1981); XLIX (23/11/1983); Numismatica Ars Classica & Spink Taisei Numismatics, Zürich, Auction 52, part I (26th October 1994), lotti 771-835.
Mondo islamico
di Maria Giovanna Stasolla
I sistemi di misura lineari, ponderali e di capacità
I pesi e le misure in uso nel mondo islamico presentavano una notevole varietà a causa della sopravvivenza, sia pure in diversa misura, dei sistemi diffusi in quel vastissimo territorio prima dell'espansione musulmana del VII e VIII secolo. Per lo studio dei pesi islamici si deve far ricorso ai dati forniti dalle fonti letterarie, all'analisi dei reperti archeologici (soprattutto dei pesi in vetro che servivano da campione) ed anche alle informazioni contenute in fonti europee, quali le guide dei mercanti. Ancora, tuttavia, le ricerche in quest'ambito non hanno prodotto risultati definitivi. I dati degli autori musulmani e le scoperte archeologiche hanno consentito comunque il calcolo dei differenti valori.
Sistemi di misura lineari
Le misure di lunghezza e di superficie, a differenza di quelle di peso e di capacità usate correntemente nelle transazioni commerciali quotidiane, erano adoperate prevalentemente da funzionari incaricati di eseguire rilievi catastali per ragioni fiscali o stime sul valore dei raccolti. Nel mondo islamico, come in molte altre culture, le fondamentali misure di lunghezza sono definite in relazione a diverse parti del corpo. Un iṣbā῾, "dito", era la larghezza della falange mediana del medio, per convenzione 1/24 del ḏirā῾, o cubito, esso stesso uguale in origine alla lunghezza del braccio tra il gomito e l'estremità del medio. La qabḏa ("larghezza del pugno") era la larghezza delle quattro dita di una mano riunite. Lo šibr ("spanna"), era l'espansione della mano dal pollice al mignolo. Il bā', o qāma, era la larghezza della due braccia distese, cioè una bracciata, canonicamente uguale a 4 ḏirā῾. La qaṣaba poteva valere da 5 a 8 ḏirā῾, indicando comunque una lunghezza media di 4 m. Nelle regioni iraniche il gaz equivaleva generalmente al ḏirā῾ arabo. Nei primi tempi dell'Islam la misura di superficie fondamentale era il ǧarīb che, pur essendo anche una misura di capacità per le granaglie, era usato per le superfici e designava inizialmente la superficie seminata con un ǧarīb di grano, ma la superficie del ǧarīb variava in misura considerevole. Canonicamente esso valeva 100 qaṣaba quadrate, cioè circa 1600 m². Nel Fars questa misura era il "piccolo ǧarīb", essendo il "grande" di 5837 m², ma in seguito il ǧarīb di Persia fu ridotto, nel XVII secolo, a 958 m². In Egitto la misura più corrente era il faddān ("giogo di bue"), definito da al-Qalqashandi nel XV secolo come equivalente a 400 qaṣaba quadrate, cioè 6368 m².
Sistemi ponderali e misure di capacità
I nomi dei pesi e delle misure di capacità ne indicano l'origine: raṭl, il peso più corrente, è una forma aramaica dal greco litron; qinṭār (100 raṭl ) nasce dal latino centenarius; qafīz è il nome persiano di una misura di capacità; il mudd corrispondeva in Iraq a circa 1,05 l, in Siria a 3,67 l, in Egitto a 2,51 l. La diversità dei pesi e delle misure designati dallo stesso termine è un fenomeno comune a tutti i Paesi musulmani. Quasi ogni distretto aveva il suo sistema e, in alcuni Paesi, i pesi e le misure della capitale erano differenti da quelli delle campagne (i geografi citano svariati esempi, fra cui il Gibal e la sua capitale Rayy, Aleppo e la sua provincia). Inoltre, pesi differenti erano usati, con lo stesso appellativo, per diverse derrate: ad esempio, in molte province la carne era pesata con un raṭl che non era lo stesso per altre merci. In tutto il mondo islamico si usavano per i cereali delle misure di capacità, diverse però da quelle usate per i liquidi. Nel corso dei secoli si affermò in molti Paesi l'uso di pesare alcuni liquidi (ad es., l'olio d'oliva) e di sostituire i pesi e le misure di capacità con unità più grandi. Nonostante le reciproche influenze, si nota comunque il persistere di una marcata differenza fra i sistemi ponderali dei Paesi arabi e di quelli persiani, eredità del passato rispettivamente bizantino e sasanide. Ne risultò una doppia struttura dei sistemi metrologici che erano decimali e sessagesimali. In questo campo l'influenza delle usanze diffuse nell'Arabia preislamica fu quasi insignificante sui Paesi conquistati: le misure di capacità usate in Higiaz ai tempi del Profeta non si diffusero in altri Paesi, tranne il ṣā῾ equivalente a 4 mudd che si ritrova in Maghreb con valori variabili. Ma l'unità fondamentale di peso in uso a Baghdad fu largamente usata come campione durante il periodo abbaside (VIII-XIII sec.). D'altra parte i sovrani musulmani non adottarono "misure reali" per la riscossione delle imposte e i pagamenti; solo alcuni crearono delle misure speciali, ma questo non costituì mai la regola. Nonostante questa diversità, i Musulmani tentarono di dare ai sistemi metrologici in uso almeno una base teorica comune adattata al sistema monetario dei califfi che fu considerato come canonico: fu così elaborata una teoria metrologica. Si suppose che ogni peso consistesse in un certo numero di dirhām-peso, diverso dal peso della moneta omonima. I pesi di vetro di epoca califfale rinvenuti in diverse regioni e i dati forniti dalle guide dei mercanti medievali e dagli autori musulmani inducono a ritenere che il dirhām-peso si aggirasse intorno ai 3 g, con una certa variabilità regionale. Un'altra unità di peso era il miṯqāl: come 10 dirhām d'argento dovevano avere lo stesso peso di 7 dīnār d'oro, ugualmente 10 dirhām-peso dovevano essere uguali a 7 miṯqāl. Le autorità di governo facevano stampigliare il valore in dirhām sui pesi-campione e gli autori arabi indicano generalmente il valore reale di un peso mediante queste unità teoriche. Erano stabilite, inoltre, altre corrispondenze: un dirhām-peso equivaleva a 60 grani di orzo (habba) equivalenti ciascuno a 70 grani di senape; un miṯqāl equivaleva a 60 grani d'orzo, ma equivalenti ciascuno a 100 grani di senape. Il miṯqāl era ugualmente diviso in 24 qīrāt in modo che il dirhām-peso fosse calcolato a 16 qirāt e 4/5. Anche il miṯqāl subiva variazioni regionali. All'epoca del Profeta e dei suoi successori, sembra che il sistema dei pesi di Babilonia fosse già stato introdotto in Arabia. Alla Mecca e in Oman ci si serviva di un raṭl che era il doppio di quello che in seguito fu chiamato il "raṭl di Baghdad" e che dunque pesava 402,348 g. L'unità di base delle misure di capacità era il mudd contenente un raṭl meccano di grano e considerato il mudd canonico dell'Islam. I dati attualmente in nostro possesso sui pesi e le misure di capacità in uso nel Medioevo in Siria e in Egitto sono molto più abbondanti rispetto a quelli di cui si dispone per altri Paesi islamici sulla base tanto dei ritrovamenti archeologici che delle informazioni fornite dalle fonti. Ci si soffermerà, dunque, sui sistemi in uso in queste regioni, mentre si rimanda ai testi citati in bibliografia per l'approfondimento sulle altre regioni del mondo islamico, particolarmente Iran e India che presentano rilevanti peculiarità. Per pesare piccole quantità si usava ovunque il raṭl: sotto gli Omayyadi equivaleva a circa 340 g, uguale cioè alla libbra romana. Nel X secolo in Siria e Palestina era in uso un raṭl pesante di circa 600 dirhām, quindi 1,853 kg, mentre quello usato a Damasco era un po' più leggero. Fra XI e XII secolo si trovano ad Aleppo, Hamat e Shayzar raṭl di peso superiore a 2 kg, mentre quello di Damasco si manteneva appena superiore ad 1,8 kg, come testimoniano le fonti arabe e le guide dei mercanti italiani che gli attribuiscono 6 libbre veneziane leggere (cioè 1,8072 kg). Ancora nei secoli XIII e XIV quello delle province della Siria settentrionale e della Palestina si manteneva superiore ai 2 kg. I cereali erano misurati in Siria meridionale e in Palestina a ġirāra, il cui volume differiva in ogni provincia: quella di Damasco era uguale a 73 mudd (contenendo il mudd 2,840 kg di grano) o 3 irdabb egiziani, cioè 208,74 kg di grano; ma a Gerusalemme la ġirāra ne conteneva, almeno alla fine del Medioevo, tre volte di più. Nella Siria settentrionale era invece in uso il makkūk, sia pure con valori differenti: quello di Aleppo e di Tripoli conteneva 83,5 kg di grano, quello di Hamat 92,77 kg secondo al-Umari e Qalqashandi, ma durante le Crociate era più piccolo: quello di Aleppo, ad esempio, si era ridotto nel XII secolo a circa 40 kg di grano. Dai pesi di vetro rinvenuti in Egitto si deduce che il raṭl-campione qui usato in epoca omayyade equivaleva a 440 g, ma gli Abbasidi ne introdussero uno appena più leggero; nello stesso periodo ci si serviva anche di un "grande raṭl " di 493 g. Sotto i Fatimidi e in epoca successiva (a partire dalla seconda metà del X fino al XIII sec.) erano in uso parecchi raṭl: quello detto miṣrī di 144 dirhām, cioè 444,9 g per pesare il pane, la carne e altri articoli; il raṭl detto fulfulī ("di pepe" perché serviva per le spezie) di 150 dirhām, cioè 463 g che si adoperava anche per il cotone; il raṭl layṯī (dal nome di un governatore) di 200 dirhām = 617,97 g per il lino; il raṭl ǧarwī di 312 dirhām = 964 g per il miele, lo zucchero, il formaggio e i metalli. Sebbene le fonti mercantili europee tendano a minimizzare le differenze regionali, è ormai accertato che la diversità dei pesi era più grande in Egitto che in Siria, perché nelle grandi città siriane molte più derrate erano pesate con gli stessi pesi. A Damasco, ad esempio, tutte le spezie e i metalli lo erano in raṭl (e qinṭār) damasceni. In Egitto, invece, le spezie erano pesate in mann (il cui valore secondo le diverse fonti varia da 753 a 840 g). Le misure di capacità usate in Egitto sotto il califfato erano il ṭillīs e diversi irdabb ma, a partire dalla metà del XI secolo, il primo, equivalente a circa 96 kg di grano, sembra essere caduto in desuetudine. L'irdabb era in origine una misura di capacità persiana, usata per molto tempo in Egitto sotto i Tolemei e i Bizantini. Quello in uso al Cairo, secondo al-Muqaddasi, conteneva 72,3 kg di grano, mentre quello del Fayyum raggiungeva i 103,22 kg (equivalenti a 9 wayba); in epoca mamelucca l'irdabb del Cairo equivaleva a 68,8 kg di grano. Per l'olio d'oliva ci si serviva, in epoca omayyade e abbaside, di misure di capacità: il qisṭ di cui sono documentati tre diversi valori (476 g; 1,07 kg; 2,14 kg), il maṭar, equivalente a circa 17 kg d'olio, che era adoperato anche per altri liquidi; sotto gli Ayyubidi si pesava l'olio in qinṭār (o raṭl ) ǧarwī. Per grandi quantità di diverse derrate ci si serviva di vari tipi di "carichi": lo ḥiml corrispondeva a 600 raṭl egiziani, cioè 266 kg, ma per le spezie valeva 500 raṭl, cioè 222,45 kg; questa unità era quella che i mercanti italiani chiamavano "sporta" e valutavano intorno alle 700 libbre veneziane leggere, cioè 217 kg circa. In Iraq, dove era presente l'antica tradizione persiana, i pesi erano diversi da quelli usati in Siria ed Egitto, sebbene alcuni avessero gli stessi nomi. Il raṭl di Baghdad, che corrispondeva a circa 400 g, era considerato come il raṭl "canonico" dei Musulmani, perché era stato adoperato a partire dai primi califfi; con questo nome si trovano, però, registrate delle misure molto diverse (da 900 g a 1,85 kg) usate nella regione mediorientale. Le misure di capacità seguivano un sistema sessagesimale. Per piccole quantità di cereali si usava il qafīz, di cui sono registrati valori differenti: da 25 a 120 raṭl di Baghdad, cioè da 10 a oltre 48 kg di grano. La misura di capacità utilizzata per più grandi quantità di cereali era il kurr, variabile da 771 a 2829 kg di grano, mentre per piccole quantità era in uso il makkūk, contenente circa 6 kg di grano ma, al tempo delle Crociate, anche quasi 15 kg di grano. La Persia, come si è detto, pur risentendo notevolmente dell'influenza arabo-islamica, conservò un proprio sistema metrologico in cui, ad esempio, l'uso di misure di capacità era scarso; tuttavia, all'epoca dei califfi, il qafīz era largamente usato. Nella Spagna musulmana si usava correntemente un raṭl di 503,08 g, ma per pesare la carne il raṭl era 4 volte più pesante. Per i cereali si adoperava un qafīz contenente 60 raṭl di grano, cioè 30,22 kg; l'olio era pesato a ṯumn di 2 raṭl = 1120 g e la qulla equivaleva a 12 ṯumn.
Bibliografia
F. Borlandi (ed.), Il Libro di mercatantie et usanze de' paesi, Torino 1936; W. Hinz, Islamische Masse und Gewichte, Leiden 1955; E. Ashtor, Histoire des prix et des salaires dans l'Orient médiéval, Paris 1969; A.K.S. Lambton, Landlord and Peasant in Persia, London 1969; M. Cook (ed.), Studies in the Economic History of the Middle East, London 1970; E. Ashtor, A Social and Economic History of the Near East in the Middle Ages, London 1976; P. Balog, Umayyad, Abbasid and Tulunid Glass Weights and Vessel Stamps, New York 1976; E. Ashtor, Levant Trade in the Later Middle Ages, Princeton 1983; H. Inalcık, Studies in Ottoman Social and Economic History, London 1985; E. Ashtor, Makāyil et Mawāzīn. I, Pays arabes, persans et turcs, in EIslam², VI, 1991, pp. 115-19; J. Burton-Page, Makāyil et Mawāzīn. II, Inde, ibid., pp. 119-20.
Iran
di Liliana Camarda
I sistemi di misura lineari, ponderali e di capacità
La gradazione di pesi in lingotti utilizzata in Medio Oriente prima di Ciro il Grande era quella nota come "standard babilonese"; il suo sistema di multipli era sessagesimale, basato su dracma o mezzo siclo, siclo (8,18 g), mina (= 60 sicli), talento (= 60 mine). Circostanze locali, insieme alla difficoltà di mantenere uno standard uniforme, portarono ad alcune modifiche in certe aree e periodi. A Ugarit, ad esempio, si utilizzò per le transazioni una mina equivalente a 50 sicli. In linea di massima fu l'unità base a subire mutamenti, più raramente il sistema di multipli. Durante il regno assiro il valore della mina reale s'innalzò, in alcune transazioni, fino ai 1010 g, ossia il doppio della mina babilonese, al fine di aumentare il tributo senza modificare l'imposta, agendo sul peso. Dario dotò il suo impero di un sistema monetario e ponderale unificato, nel quale corresse le diminuzioni e gli incrementi di peso arbitrari dei periodi assiro e neobabilonese. Il peso base in tale sistema riformato era un siclo di 8,4 g. Alcuni elementi sembrano indicare che prima di tale riforma il sistema ponderale proprio dei Persiani fosse su base decimale piuttosto che sessagesimale, ma allo stato attuale degli studi non è possibile formulare ipotesi più precise. Nel sistema achemenide riformato una nuova unità, esclusivamente persiana, entrò nell'uso comune accanto a quelle babilonesi: il karša, pari a 10 sicli. Sulle tavolette elamite provenienti da Persepoli compaiono regolarmente, nelle registrazioni di pagamenti, i termini karša, siclo, mezzo siclo (quest'ultimo in seguito identificato con la dracma attica). Ancora più giù nella scala compare il dānaka, un'unità di peso per l'argento corrispondente ad 1/8 di siclo, ossia a circa 1,05 g, che si può supporre appartenesse anch'essa all'antico sistema iranico. Il più piccolo dei pesi achemenidi riportati è noto in accadico come ḫalluru, o ḥlr nella sua forma aramaica. Il valore corrispondente sembra essere un 1/10 di siclo nei testi assiri, 1/40 di siclo, invece, in quelli aramaici. Tutte queste misure, espresse da pesi in pietra di forma piramidale, erano unità standard che l'amministrazione persiana considerava obbligatorie non solo per la Persia, ma anche per le satrapie, almeno per quanto riguardava il pagamento delle tasse reali; tuttavia, in Egitto, Babilonia e altri Paesi furono conservati anche i sistemi di misura locali. La maggior parte delle informazioni sulle unità ponderali proviene dai testi letterari, cui si affiancano tuttavia anche ritrovamenti archeologici, in special modo alcuni pesi che solo di poco si discostano, e certo a causa dell'usura, dai valori appena citati. Un peso corrispondente a 60 karša è stato ritrovato a Persepoli; dallo stesso sito ne proviene anche un altro di 120 karša (9,95 kg), sul quale è un'iscrizione trilingue che ne certifica il valore ponderale. Alcuni dei pesi ritrovati, privi di indicazione inscritta del valore nominale, potevano avere una funzione particolare, relativa forse alla pesa di una determinata quantità di monete o lingotti. Così come il sistema ponderale, anche i sistemi di misura di lunghezza, distanza e volume furono adattati dal sistema babilonese e, allo stesso modo, si possono rinvenire in essi tracce di un precedente sistema decimale. Per quanto riguarda le misure di lunghezza, la ricostruzione è piuttosto complessa e si basa su sistemi proporzionali desunti dai palazzi achemenidi. A Pasargade si individuano due moduli, il piede e il cubito, corrispondenti rispettivamente a 345 mm e a 515 mm, a Persepoli un piede di 347/348 mm e il suo quarto, un palmo di 87 mm. Questi valori sono precedenti alla riforma di Dario, per cui il piede babilonese di 330 mm potrebbe essere stato introdotto in seguito per usi ufficiali. I legami tra le antiche unità di lunghezza e di distanza persiane e quelle greche sono numerosi. Seguendo le affermazioni di Erodoto, la parasanga persiana, utilizzata per calcolare le distanze, doveva equivalere a 5,33 km, ossia 30 stadi greci. La stessa parasanga corrisponderebbe a mezzo bēru, unità babilonese, a conferma dei continui scambi tra le due civiltà. Un'altra unità di distanza probabilmente utilizzata dagli achemenidi si ritrova nell'iscrizione in aramaico dell'imperatore Ashoka a Laghman (Afghanistan), nella quale si afferma che la distanza tra questo posto e Palmira in Siria è di 200 qštn, cosicché ogni qšt equivale a 19 km, che è anche, all'incirca, la distanza tra due stazioni di posta reali nominate da Erodoto. Prendendo in considerazione le unità di lunghezza e distanza menzionate nell'Avesta, si nota che nei testi più recenti del corpus i termini riportati riflettono influenze ellenistiche, conformandosi al sistema attico-romano, mentre testi più antichi fanno riferimento ad un sistema differente, che comprende lo hāθra e il suo doppio, il tačar. Il primo dovrebbe corrispondere ad una parasanga, il secondo a due parasanghe, vale a dire un bēru babilonese. Tra le misure di capacità, quella chiamata in persiano antico irtiba o, in greco, artabe compare sulle tavolette elamite di Persepoli. Erodoto la descrive come di poco più grande del medimnus, giungendo così ad una misura per l'artabe di 55,67 l; un valore maggiore è rappresentato dall'achane, che corrisponde a 45 medimni. Altre unità di misura possono essere dedotte dai paralleli sasanidi. In un'iscrizione di Shapur si menziona il grīv o grīwa, costituito da 10 ḥōfan. La versione greca del testo fa corrispondere il grīv a 1/6 di artabe, mentre nelle tavolette di Persepoli il valore indicato equivale a 1/3 di artabe, almeno per quanto riguarda il periodo a cui esse si riferiscono. In questo caso, essendo il valore dell'ḥōfan fermamente stabilito, l'artabe dovrebbe ammontare a 27,9 l; infatti l'ḥōfan, definito come la quantità di cibo che forma la razione quotidiana di un soldato, corrisponde a 0,93 l. Un vaso da Persepoli confermerebbe questo dato. Per quanto riguarda la misurazione dei liquidi, i valori unitari non variano, pur essendo espressi con termini differenti: compare il maris, spesso citato in testi greci, corrispondente al termine elamita marriš delle tavolette di Persepoli o al mry, ripetutamente elencato su un ostrakon da Nisa, la cui sottounità è abbreviata come K, forse ad indicare il termine kapithe. Dalle tavolette di Persepoli si ricava che il marriš è la misura liquida corrispondente ad un grīwa (9,28 l) e che la sua suddivisione è il kapithe, il quale è così uguale a 1 ḥōfan. L'iscrizione di Shapur prima citata menziona un'altra unità di misura, il pās, che sembrerebbe una sopravvivenza achemenide, di cui non si conosce però il valore metrico di riferimento. Con i Seleucidi, e successivamente con i Parti, pesi e misure non furono modificati rispetto all'epoca precedente, ma furono affiancati dal sistema greco attico.
Bibliografia
G.G. Cameron, Persepolis Treasury Tablets, Chicago 1948; E.F. Schmidt, Persepolis. III, Contents of the Treasury and Other Discoveries, 2, Chicago 1957; G.G. Cameron, New Tablets from the Persepolis Treasury, in JNES, 24 (1965), pp. 167-92; M.A.R. Colledge, The Parthians, London 1967; R.T. Hallock, Persepolis Fortification Tablets, Chicago 1969; I. Gershevitch (ed.), The Cambridge History of Iran. VII, The Median and the Achaemenian Periods, 2, Cambridge 1985; M.A. Dandamaev - V.G. Lukonin, The Culture and Social Institutions of Ancient Iran, Cambridge 1989.
Subcontinente indiano
di Liliana Camarda
I sistemi di misura lineari, ponderali e di capacità
Nel Subcontinente indiano le prime testimonianze dell'esistenza di pesi e misure, indicanti un meccanismo commerciale e di regolazione dello scambio, provengono dalla civiltà dell'Indo (2600-1900 a.C. ca.). I manufatti, di calcedonio, scisto, steatite, pietre semipreziose, rame, terracotta, includono pesi di varie misure e gradazioni, oltre ad accessori quali piatti da bilancia, bilance, recipienti per misurazioni, strumenti graduati per misurazioni lineari. La mancata decifrazione del sistema di scrittura della valle dell'Indo ci priva di informazioni più precise sull'organizzazione del commercio e sulla sua eventuale dipendenza da una qualche forma di controllo statale. Pesi sono stati rinvenuti a Chanhu Daro, Mohenjo Daro, Harappa, Kalibangan, Lothal, Rojdi, Ropar e Surkotada. Essi differiscono da quelli dell'Asia Occidentale per forma, misura e materiale; la maggior parte è di forma cubica, sebbene siano stati ritrovati esemplari di forma troncosferica, cilindrica, conica e "a barile". Così come pesi di forma cubica, tipici della valle dell'Indo, sono stati ritrovati in Asia Occidentale, pesi dalla forma a barile da Harappa e Mohenjo Daro sembrano essere d'origine mesopotamica, cosa che indica un'attività di scambio tra le due aree. I pesi rinvenuti a Lothal, ove si prendano i più piccoli come unità, rientrano per la maggior parte nella proporzione semplice di 2, 4, 6, 8, 16, 32, 64, 160; un'altra serie di pesi per bilance dallo stesso sito consiste di sferoidi tronchi; una terza serie di pesi presenta una somiglianza col sistema assiro utilizzato a Susa. Ciò fa supporre che i mercanti del luogo utilizzassero lo standard harappano per le transazioni interne e uno standard aggiuntivo, simile a quello assiro, per il commercio internazionale. A Mohenjo Daro e Harappa i pesi più piccoli seguono un sistema binario, quindi la serie continua con un sistema decimale: 1, 2, 8/3, 4, 8, 16, 160, 200, 320, 640, 1600 e così via, con le frazioni dei pesi più grandi in terzi. Gli esemplari provenienti da Bargaon, di poco posteriori, sono di forma cubica, scheggiati per dar loro le dimensioni desiderate e politi; le terminazioni sono abilmente tagliate. Questo sistema ponderale, seguito in tutto il territorio vallindo e nelle sue aree d'influenza, per circa tre quarti di millennio non subì mutamenti. Il ritrovamento di pesi semilavorati a Chanhu Daro, in quella che è stata identificata come l'abitazione di un tagliatore di pietre, indica che la manifattura era locale, limitata, con ogni probabilità, a specifici centri e sottoposta a controllo e supervisione. I pesi erano poi distribuiti dove ve ne fosse richiesta, assicurando così uniformità e accuratezza al sistema di misurazione. Non sembra che i pesi fossero utilizzati da privati, ma principalmente, se non unicamente, in transazioni commerciali; essi erano reperibili in luoghi specifici, frequentati da commercianti e mercanti. Manufatti in pietra, di forma e peso corrispondenti agli esemplari harappani, sono stati ritrovati nell'isola di Bahrain, correlati a sigilli dello stile proprio del Golfo Persico. Questo farebbe pensare che i mercanti del Golfo Persico e della valle dell'Indo fossero associati in un sistema commerciale che serviva da un lato la Mesopotamia e dall'altro il Subcontinente. Per la pesatura venivano usate bilance a due piatti, ciascuno dei quali sospeso, tramite un filo passante per tre fori, ad una delle terminazioni del giogo. Bilance di piccole dimensioni erano utilizzate per la pesatura di metalli e pietre preziose. I ritrovamenti di bilance sono relativamente rari, probabilmente a causa del fatto che il materiale più utilizzato per la loro fabbricazione era il legno. Tra gli esemplari rinvenuti si segnalano piatti da bilancia in metallo e terracotta; una barra di rame o bronzo, rinvenuta in associazione con un paio di essi, è probabilmente da interpretare come un giogo, dato che una delle terminazioni conserva i resti di un filo al quale era forse sospeso il piatto. Una bilancia di terracotta, con due fori per sospensione, è stata ritrovata a Surkotada. Strumenti graduati per misurazioni lineari, provenienti da Kalibangan, Lothal, Mohenjo Daro e Harappa, sembrano seguire un sistema decimale. L'esemplare da Mohenjo Daro presenta una serie regolare di tacche, che segnano subdivisioni di 6,7056 mm: su una di queste vi sono un foro e a cinque tacche di distanza un cerchio; è ragionevole supporre che il foro successivo fosse su una decima tacca, mancante. Uno strumento dello stesso tipo, rinvenuto a Lothal, presenta uno spazio tra due linee di 1,7 mm; venti di queste subdivisioni corrispondono approssimativamente alla distanza tra il foro e il cerchio (33,4 mm, ossia 1,32 pollici) nell'esemplare da Mohenjo Daro, rispetto al quale, dunque, lo strumento di Lothal rappresenta un grado di precisione più elevato. È possibile che esistessero strumenti analoghi destinati alla misurazione di grandi superfici, utilizzati, ad esempio, per l'edilizia. In tal caso l'unità di misura potrebbe essere stata diversa; è ipotizzabile che essa corrispondesse a 68 mm, cioè 40 volte la già citata unità di 1,7 mm e, grosso modo, la distanza tra due fori sullo strumento di Mohenjo Daro (67,056 mm). Oltre al pollice e al piede, altra unità di misura lineare impiegata era il cubito, come si evince da una bacchetta di bronzo da Harappa; l'uso simultaneo dei due sistemi di piedi e cubiti è suggerito inoltre dalle misure stesse di edifici a Harappa e Mohenjo Daro. Le dimensioni del cubito variano qui da 51,8 a 53,6 cm (da 20,3 a 20,8 pollici); il piede, di 33,5 cm circa (13,2 pollici), sembra aver avuto le stesse dimensioni a Mohenjo Daro e Lothal. Per quanto concerne invece le misure di capacità, il sistema adottato in epoca harappana resta ancora sconosciuto. Un certo numero di sfere, cilindri e dischi di pietra, dalla superficie polita, utilizzati con ogni probabilità come pesi, sono stati ritrovati negli insediamenti calcolitici dell'India centrale e del Deccan settentrionale (Maheshwar, Navdatoli, Chandoli e Nevasa). La loro serie segue il rapporto di 1, 2, 4, 6, 8 e così via. Quasi tutti i siti della valle del Gange di epoca storica hanno restituito oggetti circolari di terracotta, a superficie piatta, concava o convessa, semplici o decorati. Noti in letteratura come "dischi", non è ancora chiaro se si tratti di una serie di pesi; sembrano esserlo, a giudicare dalle dimensioni, quelli rinvenuti a Harigaon (Nepal), di periodo Kushana (I-III sec. d.C.). Di epoca storica sono anche oggetti sferici in vari materiali, identificati come pesi e provenienti da Taxila e Charsada nel Nord-Ovest, Kaundinyapura, Besnagar ed Eran nell'India centrale, Rang Mahal in Rajasthan, Vadnagar in Gujarat, Salihundam in Andhra Pradesh. Molti di quelli ritrovati a Taxila presentano piccoli incavi sulla superficie, forse marchi ufficiali del peso standard. L'incavo era riempito di piombo, la cui quantità variava a seconda che il peso dovesse essere ridotto o incrementato. Il sistema usato segue il rapporto di 1, 2, 4, 8, 16, ecc., con l'unità campione che si aggira intorno ai 52-53 g, equivalente al peso standard delle monete punzonate. Un esemplare di diverso tipo proviene da Kaundinyapura: si tratta di un peso sferoidale di diaspro, attribuito ad epoca Maurya, che presenta un polo appiattito. È stato ipotizzato che questo ritocco intendesse ridurne il peso per renderlo conforme all'antico standard tolā di 180 grani (11,663 g); a un tolā corrisponde esattamente un peso per gioiellieri in calcedonio, rinvenuto a Maheshwar. Da Besnagar proviene invece un peso di rame sfaccettato. A Taxila sono stati riportati alla luce piatti da bilancia di rame e ferro, databili al 300 a.C. - 500 d.C., con due ganci per sospensione, oltre ad un piccolo vaso di terracotta, di epoca Maurya (IV-II sec. a.C.), con un forellino sul fondo, probabilmente una coppa-misurino; un altro vaso, simile a questo, ha l'interno diviso in tre compartimenti. Una varietà di pesi piramidali in terracotta è stata individuata in livelli del 200 a.C. - 200 d.C. a Charsada. Da Salihundam provengono invece pesi a forma di prisma. Le testimonianze archeologiche provano che i pesi standard prevalgono nei periodi Kushana e Gupta. Da livelli del II-VI sec. d.C. di siti quali Sanghol, Rang Mahal, Bhita, Kaushambi, Vaishali, Nagarjunakonda, Vadnagar provengono infatti tavolette di terracotta della stessa forma, marcate da linee o sottili tratti che le dividono in due, tre o quattro compartimenti; le dimensioni ridotte fanno pensare che fossero utilizzate da gioiellieri. Un'asta per pesatura di ferro (un lungo giogo con una protuberanza su una terminazione), databile all'VIII sec. d.C., proviene da Sirpur, mentre aste simili, contrassegnate da tacche, sono rappresentate in sculture provenienti da Amaravati, Nagarjunakonda e dal Gandhara, che ne documentano l'esistenza nei primi secoli dell'era cristiana. Per quanto riguarda le fonti scritte, l'Arthaśāstra ("Scienza dell'utile", IV sec. a.C. ca.), il Mānavadharmaśāstra ("Il codice di Manu", la cui prima versione conosciuta è datata tra il II sec. a.C. e il II sec. d.C.), l'epica, il canone Jaina e altre opere letterarie mostrano chiaramente che i rapporti socioeconomici che legano Stato ed individui si sono evoluti nel corso del tempo. Leggi che regolano il commercio si ritrovano in diversi testi. Nell'Arthaśāstra, ad esempio, è elencata una serie di funzionari statali che avevano il compito di sorvegliare commercio e industria. Tra questi compare un sovrintendente a pesi e misure, custode delle diverse unità correnti, il quale controllava che quelle usate corrispondessero al sistema vigente e riscuoteva una tassa per il loro utilizzo; rientrava inoltre nelle sue funzioni il rilascio delle licenze, obbligatorie per l'esercizio di qualunque attività di carattere commerciale. Da altri testi si apprende che in epoca Kushana i pesi e le misure dovevano essere correttamente marcati ed esaminati ogni sei mesi e che le contraffazioni di bilance e strumenti di misura erano punite con multe severe. Non sappiamo però fino a che punto tali norme fossero seguite, dal momento che i testi non indicano un controllo rigido da parte dello Stato. Un'iscrizione di Huvishka da Mathura, del II sec. d.C., riporta i termini āḍhaka, ghaṭaka, prastha, i quali indicano alcune unità di misura ponderali. Nel canone Jaina sono riportate regolamentazioni riferite a pesi e misure, oltre ai nomi di cinque tipi di pesi. Altri testi documentano che lo standard ufficiale del peso era fissato su un valore leggermente inferiore a quello pubblico, così da garantire un margine di guadagno del 5%. Il peso base dell'India antica era il raktika, basato sul seme del guñja e convenzionalmente stimato in circa 1,83 grani (0,118 g); numerose fonti indicano serie di pesi costituite da multipli e sottomultipli di questa unità (il Mānavadharmaśāstra ne riporta una utilizzata dagli orefici), ma nel corso del tempo e nelle diverse regioni del Subcontinente gli standard variarono notevolmente, portando a serie non compatibili fra loro. Nel Divyāvadāna sono riportati termini che si riferiscono a misure di capacità; altre fonti, tra cui l'Arthaśāstra, riportano unità di misura lineari, tra cui lo yojana, l'unità di misura per le lunghe distanze più comune dell'India antica, corrispondente a 7,2 km in alcuni testi e a circa il doppio in altri.
Bibliografia
J.H. Marshall, Mohenjo-daro and the Indus Civilization, I-III, London 1931; H.G. Rawlinson, India, London 1937; J.H. Marshall, Taxila, I-III, Cambridge 1951; R.E.M. Wheeler, The Indus Civilization, Cambridge 1953; A.L. Basham, The Wonder that Was India, London 1954; H.D. Sankalia, Some Aspects of Prehistoric Technology in India, New Delhi 1970; S.R. Rao, Lothal and the Indus Civilization, London 1973; R.N. Saletore, Early Indian Economic History, London 1975; B. Allchin - R. Allchin, The Rise of Civilization in India and Pakistan, Cambridge 1982; K. Prasad, Cities, Crafts and Commerce under the Kuṣāṇas, Delhi 1984; B.R. Mani, The Kushan Civilization, Delhi 1987; A. Ghosh, An Encyclopaedia of Indian Archaeology, Leiden 1990; G. Verardi, Excavations at Harigaon, Kathmandu, I-II, Rome 1992; B.B. Lal, The Earliest Civilization of South Asia, New Delhi 1997.
Africa
di Samou Camara
I sistemi di misura lineari e ponderali
Dal VI al XV sec. d.C. le unità monetali e quelle di peso e misura svolsero in Africa un ruolo determinante negli scambi di oro, cola, cotonate, rame, sale, avorio, ecc., sia sulle rotte commerciali interne, come quella dalle savane sudanesi alle regioni di foresta, sia in quelle interregionali, come quella dal centro del continente verso le regioni sahariane o verso le coste orientali. Se i dati, specie quelli archeologici, circa le monete sono relativamente abbondanti, quelli sulle unità di peso e misura sono invece rari, avendo il baratto dominato la maggior parte degli scambi. La produzione di pesi per oro, avviata a partire dal XVI sec. d.C. nei Paesi Baoulé per sopperire alla domanda europea, ha mascherato l'esistenza, nei cinque o sei secoli precedenti, di sistemi ponderali legati alla raccolta dell'oro nelle aree di produzione, alla sua vendita sui mercati locali e alla sua esportazione. I Lobi del Burkina Faso designavano il pacchetto d'oro di 20 g con il termine barekere o badafiri; il termine barifiri era impiegato dai commercianti di Djenné. In area Mande le principali unità di misura erano il nonkon, o cubito, il sibidi, distanza tra le due estremità del pollice e del medio di una mano aperta, il segna, equivalente a un piede, e il senda, corrispondente a un passo, impiegato per misurazioni al suolo. I contatti con i Musulmani delle regioni settentrionali portarono all'introduzione nei circuiti della savana e probabilmente in quelli della foresta del miṯqāl (unità convenzionale di peso per l'oro in uso nel mondo musulmano, corrispondente a 4,25 g) come unità di riferimento nel commercio dell'oro. Durante l'VIII sec. d.C. nel regno del Ghana l'oro veniva scambiato a Kumbi Saleh, Awdaghost e Gao con il sale fornito dai mercanti musulmani. Nel XIII sec. d.C. a Niani, capitale del Mali, così come nei Paesi del Sud, barrette di rame importate dal giacimento di Takkeda erano vendute al peso del miṯqāl d'oro, vale a dire 100 miṯqāl per 2/3 d'oro. Le barrette più spesse erano vendute a un miṯqāl d'oro ogni 400, mentre quelle sottili a un miṯqāl ogni 600-700. In queste regioni, l'importanza del sale e soprattutto la sua rarità conferirono a questo bene il valore di moneta: un mucchietto di sale era scambiato contro un mucchietto d'oro. I cauri vennero utilizzati non solo come moneta, ma anche come unità ponderale sia nel Mali (XIII sec. d.C.), sia in area Hausa (XVI sec. d.C.) per scambiare oro e ottenere prodotti distribuiti dai mercanti.
Bibliografia
M. Adamu, Les Hawssa et leurs voisins du Soudan Central, in Histoire générale de l'Afrique, IV, Paris 1985, pp. 293-329; D.T. Niane, Le Mali et la deuxième expansion manden, ibid., pp. 141-96; J. Devisse, Or, in Vallées du Niger (Catalogo della mostra), Paris 1993, pp. 344-57.
Americhe
i sistemi di misura lineari, ponderali e di capacità: mesoamerica
di Michael E. Smith
Gli antichi sistemi di misura mesoamericani sono scarsamente conosciuti. I beni erano calcolati per numero e per volume, non per peso, e nei siti archeologici non sono state identificate unità ponderali standardizzate. Molti dati sui tipi di misure provengono da fonti documentarie sul Messico centrale; essi sono però spesso oscuri, in quanto dopo la Conquista le nozioni e le unità di misura dei nativi vennero rapidamente confondendosi con quelle spagnole e i documenti riportano queste ibride misure coloniali. Nonostante ciò, le ricerche condotte da V.M. Castillo e da altri studiosi hanno consentito di identificare un certo numero di unità di misura Nahuatl (azteche), che furono probabilmente in uso anche presso altre società mesoamericane. Hernán Cortés e altri tra i primi cronisti spagnoli sono molto espliciti nel riferire che nei mercati i beni erano venduti per numero e volume e che non esistevano unità standardizzate di peso. L'unica unità ponderale comunemente usata era il tlamamalli (sp. carga), il peso di un carico di solito trasportato da un portatore di professione, corrispondente a circa 23 kg. Gli spostamenti dei portatori, che recavano generalmente sia beni commerciali, sia tributi, fornivano anche due unità di distanza, il cennecehuilli e il cennetlalolli, che indicavano lo spazio percorso tra due luoghi di sosta (5 km ca.; dopo la Conquista questa unità si fuse con la legua spagnola). Unità minori di lunghezza erano basate sul corpo umano. Si conoscono le denominazioni di un gran numero di tali unità, che variavano da pochi centimetri a pochi metri e comprendevano dita, palmi, mani, avambracci, braccia, la lunghezza delle braccia distese e l'altezza. Molte unità di lunghezza, così come altri sistemi di misura, erano riservate ad ambiti specifici: ad esempio, il quahuitl (2,5 m) veniva utilizzato per misurare l'estensione dei campi agricoli. Alcuni registri delle terre dell'area del lago Texcoco comprendevano sia le dimensioni lineari dei campi, sia una misura dell'area espressa in quahuitl. Così come in lingua Nahuatl esistevano numerosi termini per le unità di lunghezza, allo stesso modo ve ne erano molti per quelle di capacità, che andavano da una "goccia" di un liquido (impiegata per misurare sostanze medicinali) a numerose tonnellate (misurazioni di granaglie e acqua). Tali unità non avevano un valore standardizzato che ne consentisse l'uso in diversi ambiti. I beni scambiati nei mercati o versati come tributi erano computati sia mediante semplici quantità di beni, sia per quantità basate sui loro contenitori. I sistemi di calcolo mesoamericani impiegavano una base di 20 unità e varie quantità erano rappresentate da simboli pittografici: un punto stava per un'unità, una bandiera per 20, una piuma per 400 e una borsa per incenso per 8000. L'importanza del sistema numerico vigesimale è attestata dalle unità impiegate per misurare semi di cacao, la principale unità monetale mesoamericana. Per transazioni al dettaglio, i semi di cacao venivano contati in multipli di 20, mentre per quantità maggiori esistevano termini per 400 (zontle), 8000 (xiquipil ) e 24.000 semi (quantità definita dagli Spagnoli carga); quest'ultimo era il carico di un portatore, equivalente a un tlamamalli. Molte delle più dettagliate informazioni sui sistemi di misura di beni provengono dalla lista imperiale dei tributi costituita dal Codice Mendoza, dove sono riportate le pittografie dei prodotti versati dalle province tributarie, corredate dalle descrizioni in spagnolo delle immagini. Il tributo in liquidi era misurato dalle quantità di giare fittili di piccole e grandi dimensioni. Nel Codice Mendoza le due dimensioni delle giare da trasporto sono chiaramente differenziate e standardizzate, ma gli archeologi non sono riusciti ad individuare tali manufatti all'interno della produzione fittile rinvenuta in siti aztechi. Vari beni solidi erano conteggiati mediante le quantità di ampie ceste, che sembrano anch'esse, stando alle loro raffigurazioni, di dimensioni standardizzate; tra questi beni vi erano semi di cacao, peperoncini essiccati, cotone grezzo e limone in polvere. Nella lista dei tributi figurano anche altre quantità di beni contenuti in piccole ceste, entro borse, in barili di legno o ciotole di ceramica e di zucca. I più comuni beni versati dalle province tributarie, le stoffe (mantas) di cotone, erano contati in involti di 20 pezzi. Dai dati disponibili si rileva l'assenza di unità standardizzate che potessero essere impiegate in ambiti diversi: tra gli Aztechi vi erano numerosi termini Nahuatl per misurazioni di lunghezza, area, capacità e quantità, ma molte unità si sovrapponevano nelle loro grandezze ed erano impiegate per fini diversi. I beni non erano misurati attraverso il loro peso, eccetto che per il carico di un portatore. Quest'ultima unità, il tlamamalli, era infatti la più standardizzata unità di misura azteca, ad attestare la centralità del trasporto umano nei trasferimenti di beni commerciali e di tributi, che nell'economia mesoamericana del Periodo Postclassico furono di imprescindibile importanza.
Bibliografia
W. Borah - S.F. Cook, Price Trends of Some Basic Commodities in Central Mexico, 1531-1570, Berkeley 1958; B. Leander (ed.), Códice de Otlazpan, México 1967; V.M. Castillo, Unidades nahuas de medida, in EstCultNáhuatl, 10 (1972), pp. 195-223; H.R. Harvey - B.J. Williams, Aztec Arithmetic: Positional Notation and Area Calculation, in Science, 210 (1980), pp. 499-505; F.F. Berdan - P.R. Anawalt (edd.), The Codex Mendoza, Berkeley 1992.
I sistemi di misura lineari, ponderali e di capacità: america meridionale
di Duccio Bonavia
Sebbene sia un dato ormai acquisito che le culture precolombiane delle Ande Centrali elaborarono sistemi di misura, molte informazioni in merito sono andate perdute per l'assenza di fonti scritte antecedenti alla Conquista e per la mancata comprensione della cultura indigena da parte dei conquistadores. In realtà tali sistemi di misura non furono inferiori per complessità a quelli impiegati nell'Europa medievale. Le informazioni relative al periodo pre-Inca sono quelle più lacunose; i dati sui sistemi metrologici Inca sono invece relativamente più abbondanti, sebbene ‒ come segnalato da J. Rowe ‒ essi siano così dispersi e non sistematizzati da dare l'impressione che questa cultura non abbia elaborato specifiche categorie standardizzate. Occorre inoltre considerare che nei resoconti dei cronisti spagnoli vi è molta ambiguità (da queste fonti sembra, ad es., che vi fossero più termini in lingua Aymara che non in lingua Quechua e spesso essi si confondono). Il sistema di misura in uso presso gli Inca era basato su alcune parti anatomiche umane. Probabilmente la lunghezza del dito (rok'ana) era una misura Aymara e non Quechua. Esisteva poi il yuku (equivalente al palmo spagnolo), la distanza dall'estremità del pollice a quella dell'indice, mantenuti quanto più possibile separati (12-14 cm ca.). La distanza k'apa corrispondeva al palmo spagnolo (20 cm ca.), mentre il khococ, vale a dire la lunghezza dal gomito fino all'estremità della mano (45 cm ca.), equivaleva al cubito. La misura più lunga ricavata sulla base del corpo umano era il braccio (rikra), equivalente a 162 cm circa e corrispondente alla distanza tra i pollici di un uomo con le braccia estese orizzontalmente. Tale lunghezza era suddivisa in "mezze braccia", definite sikya (0,8 m ca.). Il braccio (cota k'aspi) era l'unità legale e standardizzata delle misurazioni agrarie, per le quali veniva impiegato un palo di questa lunghezza; era anche in uso un regolo formato da due pali che scorrevano uno sull'altro e che consentivano di misurare esattamente un determinato spazio. Per misurare le distanze percorse in viaggio si utilizzava il passo (thatkiy), ma nelle strade Inca la misura era il topo o tupu; cippi erano collocati a distanze di circa 1,5 leghe spagnole (6285 m ca.). Murúa riporta che il topo equivaleva a 6000 passi: il dato sembra esatto, dal momento che è stato calcolato che un passo Inca corrispondeva a 1,3 m. La lunghezza equivalente a 30 topo era denominata guamany o wamani. Sappiamo che per il tracciato delle città venivano utilizzate cordicelle, ma su di esse non si possiedono dati circostanziati. Sembra che il topo venisse impiegato anche per misurazioni di aree, sebbene su questo punto esistano dubbi e i cronisti spagnoli forniscano versioni divergenti. Secondo il cronista padre Cobo si tratterebbe di un'area della lunghezza di 50 braccia (914 m ca.) per 25 braccia di larghezza (457 m ca.). Esisteva anche una misura particolare, denominata panpacancha, che equivaleva a 256 m circa e che risulta di difficile comprensione secondo i parametri occidentali, dal momento che conteneva allo stesso tempo i concetti di area, suolo, tempo e clima. Secondo padre Cobo non esistevano unità di misura standardizzate per i liquidi, per i quali generalmente si impiegavano giare. Per le granaglie era utilizzato il ccullu o phoqca, che equivaleva a circa 1/2 fanega spagnola, ma che nella stessa Spagna variava di regione in regione e corrispondeva a circa 48 l. Generalmente per questa misurazione si impiegava una grande zucca, ma potevano essere utilizzati anche recipienti di legno o argento. Nel Collao l'unità di misura dei gruppi Aymara era il sacco, che corrispondeva approssimativamente a una fanega (97 l ca.). Altra unità di misura era il runcu, usato per lo più per la coca e il peperoncino, ma anche per il cotone; esso era impiegato per le inventariazioni nei depositi reali. Venivano fabbricate ceste corrispondenti a questa misura; sappiamo che per la coca essa equivaleva a 9 kg. Sulla costa centrale peruviana per gli aridi veniva utilizzato il siquis, equivalente a 1/2 almud di Castiglia (15 l ca.); presso gli Aymara esisteva una misura simile, definita topo o tupo, che equivaleva a 45 l circa. Una misura popolare era il poctoy, corrispondente alla almozada spagnola, cioè alla quantità di un elemento fluido che poteva essere contenuta nella cavità formata dalle due mani congiunte. Nel mondo andino erano conosciute la bilancia a piatto (aysana) e quella romana, ma i cronisti spagnoli forniscono scarse indicazioni in merito. Dalle evidenze archeologiche si è a conoscenza che le bilance erano di piccole dimensioni (mediamente potevano pesare fino a 230 g ca.) e le fonti coloniali riportano che esse erano utilizzate essenzialmente per oro e argento. Gli esemplari noti sono di epoca tarda e risalgono al Periodo Intermedio Recente e all'Orizzonte Recente. In merito al computo del tempo, in lingua Quechua esistono due espressioni per la bollitura della patata, che vennero utilizzate come equivalenti dell'ora: esse sono "alcune cuociono molto" (hok yanoy chika) e "alcune cuociono" (hokeayk'oy). Un'altra misura di tempo impiegata nel passato e a tutt'oggi in uso tra i portatori è la cocada o chacchada. Essa corrisponde al tempo necessario perché durante il cammino un portatore percepisca gli effetti della masticazione del bolo di coca (chiamato acullico nell'area del Callejón de Huaylas). Questo tempo è variabile a seconda che si tratti di un percorso in salita, di un tratto pianeggiante o di una discesa e ha termine quando il portatore si siede per preparare un altro bolo. Sulla sierra, per chi chieda indicazioni in merito alla distanza di un certo luogo è normale sentirsi rispondere che essa "equivale a un certo numero di chacchadas". L'età di un individuo era calcolata in cicli vitali e non esisteva un concetto che la esprimesse in anni: gli uomini erano "misurati" in base alla loro condizione fisica e alle loro capacità. La popolazione di un chiefdom veniva invece contata attraverso un sistema decimale (10, 100 e 1000 individui). R. Larco Hoyle ha ritenuto di individuare un'unità di misura standardizzata in uso nel periodo pre-Inca; le sue ipotesi non hanno comunque trovato conferme. Egli ha osservato che la larghezza media delle strade Moche è di 9,8 m e che quella di molti monumenti risalenti alla stessa epoca è di 98 m; da ciò ha postulato che 98 cm dovesse essere la misura standard.
Bibliografia
A. Raimondi, El Perú, I, Lima 1874, pp. 69-70; E. Nordenskiöld, Emploi de la balance romaine en Amérique du Sud avant la conquête, in JSocAmer, 13, 2 (1921), pp. 169-71; P. Rivet, La balance romaine au Pérou, in L'Anthropologie, 33 (1923), pp. 535-38; R. Larco Hoyle, A Culture Sequence for the North Coast of Perú, in HSAI, II, pp. 149-75; J.H. Rowe, Inca Culture at the Time of the Spanish Conquest, ibid., pp. 183-330; W.C. Bennett, Numbers, Measures, Weight, and Calendars, ibid., V, pp. 601-19; M. Rostworowski de Diez Canseco, Pesas y medidas en el Perú Pre-hispánico, in Actas y Trabajos del II Congreso Nacional de Historia del Perú, II, Lima 1962, pp. 103-15; Ead., Mediciones y cómputos en el Antiguo Perú, in CuadPrehisp, 6 (1978), pp. 21-48.