glissosimmetria

glissosimmetria

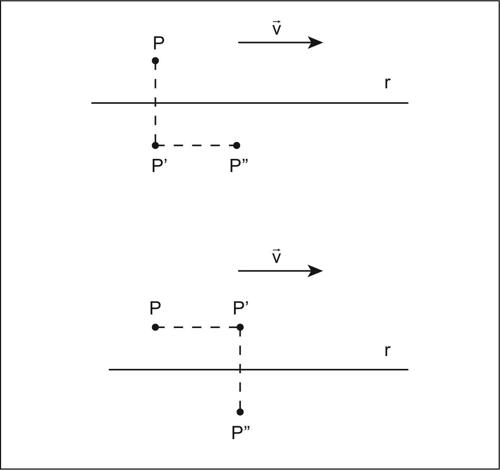
glissosimmetria nella geometria del piano, particolare isometria, detta anche antitraslazione o glissoriflessione, ottenuta come prodotto di una simmetria assiale e di una traslazione di vettore parallelo all’asse della simmetria. Fissati una retta r e un vettore v parallelo a r, la glissosimmetria relativa a r e v è la corrispondenza biunivoca tra i punti del piano tale che a ogni punto P fa corrispondere il punto P″ ottenuto mediante traslazione di vettore v del punto P′, simmetrico di P rispetto a r. Il punto P″ si ottiene anche applicando prima la traslazione di vettore v e successivamente la simmetria rispetto alla retta r.

Mentre in generale il prodotto (composizione) di due isometrie non è commutativo, nel caso della glissosimmetria il risultato è indipendente dall’ordine in cui sono composte la simmetria e la traslazione. Le glissosimmetrie sono isometrie invertenti, cioè modificano l’orientamento dei punti del piano: infatti sono composte da una isometria invertente, la simmetria assiale, e da una isometria non invertente, la traslazione. Una glissosimmetria, così definita, si ottiene dalla composizione di tra simmetrie assiali, due delle quali abbiano assi paralleli. Il termine si usa anche per indicare la composizione di tre simmetrie assiali con assi mutualmente incidenti in punti diversi: in tale caso si ha la composizione di una rotazione e una simmetria assiale.