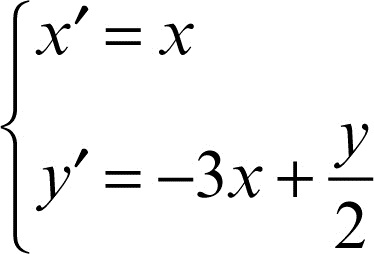funzione, grafico di una

funzione, grafico di una

funzione, grafico di una rappresentazione, nel piano cartesiano nel caso di funzioni di una variabile, dei punti (x, ƒ(x)) in corrispondenza mediante la funzione. La rappresentazione può esprimere soltanto l’andamento qualitativo che interpreta geometricamente il legame funzionale (grafico qualitativo): gli intervalli in cui essa è positiva o negativa, la sua crescenza o decrescenza, il suo andamento agli estremi del dominio. Oppure può riportare i valori esatti calcolati in corrispondenza di alcuni valori del suo dominio e sintetizzati in una tabella; tale tabulazione di valori corrispondenti permette di individuare nel piano cartesiano un insieme di punti appartenenti al grafico della funzione e di approssimare il suo andamento grafico negli intervalli tra due successivi punti individuati attraverso l’esame della sua espressione analitica. Dall’analisi di una funzione è possibile ricavare alcune caratteristiche del grafico; per esempio, se ƒ(−x) = −ƒ(x) allora il grafico è simmetrico rispetto all’origine degli assi e la funzione è dispari, se invece ƒ(−x) = ƒ(x) la funzione è pari, il che corrisponde a una simmetria del grafico rispetto all’asse delle ordinate. Il grafico delle funzioni più usuali è ricavabile da quello delle funzioni elementari attraverso opportune trasformazioni (simmetrie, traslazioni, omotetie, affinità). Per esempio, il grafico della funzione

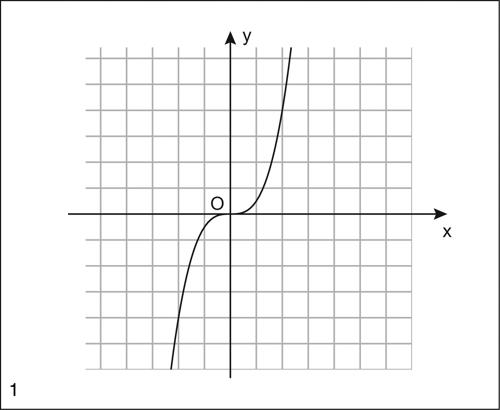
è quello rappresentato in figura 1); con la trasformazione geometrica di equazioni:

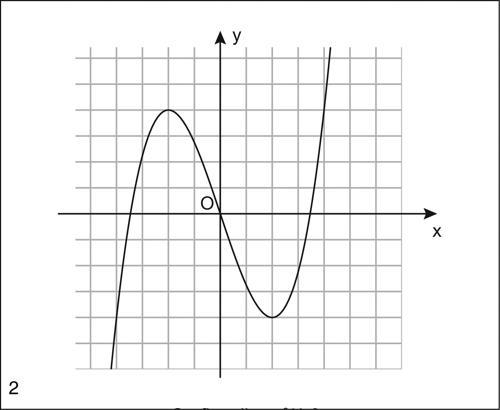
si trasforma in quello in figura 2). L’espressione algebrica della funzione corrispondentemente si trasforma in

Il grafico in figura 2) è appunto la rappresentazione cartesiana di questa nuova funzione.

I grafici delle funzioni reali di una variabile reale sono caratterizzati dal fatto che ogni parallela all’asse delle ordinate li interseca al più in un punto. La nozione si generalizza senza problemi concettuali al caso X × Y ⊆ R^n+m; tuttavia il termine grafico viene impiegato in senso esteso anche quando gli insiemi X e Y sono di tipo più generale (per esempio, spazi di Banach) e quindi non vi è più alcuna possibilità di rappresentazione grafica.