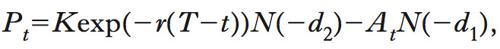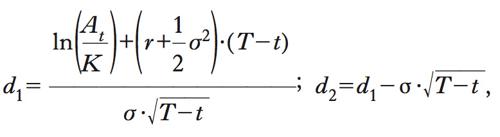opzioni, greche delle
opzioni, greche delle
Indicatori della sensibilità del prezzo di un’o. a variazioni dei parametri che lo influenzano. Il prezzo di un’o. (o anche di altri derivati) è funzione di un certo numero di variabili indipendenti. Per es., nelle formule di Black-Scholes (➔ Black-Scholes, formula di), che danno il prezzo teorico di o. plain vanilla call e put europee (➔ opzioni europee) su sottostante rappresentato da un titolo azionario, compaiono come variabili indipendenti il prezzo corrente del sottostante At, il prezzo di esercizio K, la vita residua T−t dell’o., il tasso istantaneo di interesse dell’attività non rischiosa r, la volatilità σ del sottostante. Mentre il prezzo di esercizio non cambia durante la vita dell’o., le altre variabili si modificano certamente (come la vita residua) o quasi certamente (come il prezzo del sottostante) o possono comunque modificarsi (tasso di interesse e volatilità).
Funzioni delle greche di un’opzione
Le greche di un’o. esprimono la sensibilità del prezzo dell’o. a variazioni locali di una delle variabili indipendenti. In opportune condizioni di regolarità, esse sono le derivate parziali del prezzo dell’o. rispetto a una singola variabile. In particolare, Δ (Delta) è la derivata rispetto al prezzo del sottostante, Θ (Theta) la derivata rispetto alla vita residua, Ρ (Rho) la derivata rispetto al tasso di interesse, Vega la derivata rispetto alla volatilità; a esse si aggiunge Γ (Gamma), che è la derivata parziale seconda rispetto al prezzo, ossia la derivata parziale rispetto al prezzo della funzione Delta. Ricordando che la formula di Black-Scholes è, per una call, Ct=AtN(d1)−Kexp(−r(T−t))N(d2) e, rispettivamente, per una put,
dove i coefficienti N(d), compresi fra 0 e 1, sono le probabilità che una distribuzione normale standard assuma determinazione inferiore a d e:
risulta Δ=N(d1) per una call o, rispettivamente, N(d1)−1 per una put. Inoltre, il Δ di un portafoglio (➔ p) è la combinazione dei Δ delle singole attività pesate per il numero delle rispettive unità in portafoglio. Poiché il Δ di un’azione rispetto a sé stessa è ovviamente 1, se ne deduce che un portafoglio Π, composto da una posizione lunga (➔ posizione) in Δ unità del sottostante e una corta in un’o. (con quel Δ), ha Δ(Π)=Δ1−1Δ=0 ed è dunque perfettamente coperto dal rischio di (piccole) variazioni di prezzo del sottostante (in linguaggio finanziario, neutrale rispetto al Delta). Per tale motivo, Δ è detto rapporto di copertura (➔ copertura). Peraltro, la copertura è locale, dunque richiede di essere aggiornata quando cambiamenti nei valori delle variabili, in particolare del prezzo del sottostante, modificano il rapporto di copertura stesso. Il Γ di call e put plain vanilla è pari a N′(d1)/A(T−t)1/2 σ, dove N′(d1) indica la densità in d1 di una normale standard. Per concludere, si evidenzia che per o. put e call plain vanilla risulta Vega pari a A(T−t)1/2′(d1) e Rho pari a K(T−t)exp(−r(T−t))N(d2) per una call e −K(T−t)exp(−r(T−t))N(−d2) per una put.