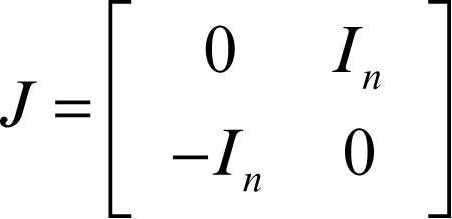gruppi classici

gruppi classici

gruppi classici in algebra, gruppi di matrici definiti come particolari gruppi di trasformazioni lineari di spazi vettoriali o proiettivi. Se M_n(R) e M_n(C) indicano le algebre delle matrici quadrate di ordine n a coefficienti rispettivamente in R e in C, allora i gruppi classici sono i seguenti:

• gruppo generale lineare reale:

coincide con il gruppo degli endomorfismi invertibili di Rⁿ in sé stesso;

• gruppo speciale lineare reale:

coincide con il gruppo degli endomorfismi di Rⁿ in sé stesso con determinante 1;

• gruppo ortogonale reale:

dove A^T è la matrice trasposta di A: coincide con il gruppo dei movimenti rigidi di Rⁿ in sé stesso che lasciano fissa l’origine;

• gruppo speciale ortogonale reale:

coincide con il gruppo dei movimenti rigidi di Rⁿ in sé stesso che ne preservano l’orientazione e lasciano fissa l’origine;

• gruppo simplettico reale:

dove

coincide con il gruppo degli endomorfismi di R²ⁿ in sé stesso che preservano la forma bilineare associata alla matrice J;

• gruppo generale lineare complesso:

coincide con il gruppo degli endomorfismi invertibili di Cⁿ in sé stesso;

• gruppo speciale lineare complesso:

coincide con il gruppo degli endomorfismi di Cⁿ in sé stesso con determinante 1;

• gruppo unitario:

dove A^H è la matrice trasposta coniugata di A: coincide con il gruppo degli endomorfismi di Cⁿ in sé stesso che preservano il prodotto hermitiano canonico di Cⁿ;

• gruppo speciale unitario:

coincide con il gruppo degli endomorfismi di Cⁿ in sé stesso con determinante 1 che preservano il prodotto hermitiano canonico di Cⁿ;

• gruppo proiettivo lineare reale:

dove ~ è la relazione di equivalenza definita da A ~ A′ se A′ = λA, ∃λ ∈ R: coincide con il gruppo delle proiettività dello spazio proiettivo reale P(Rⁿ⁺¹);

• gruppo proiettivo lineare complesso:

dove ~ è la relazione di equivalenza definita da A ~ A′ se A′ = λA, ∃λ ∈ C; coincide con il gruppo delle proiettività dello spazio proiettivo complesso P(Cⁿ⁺¹).