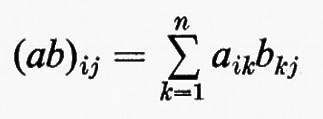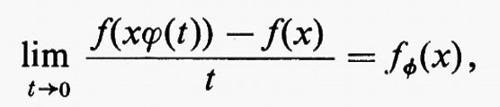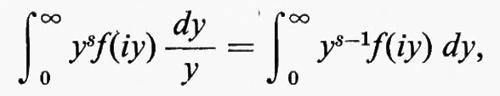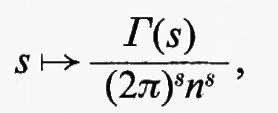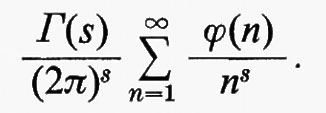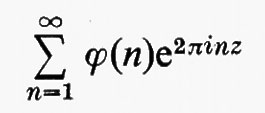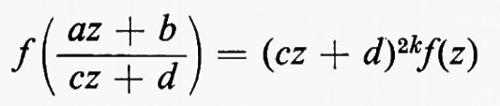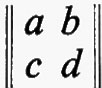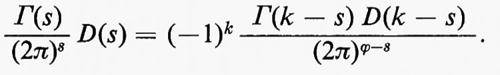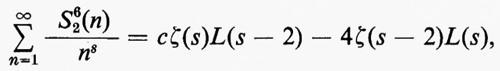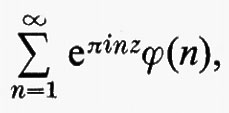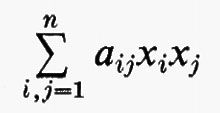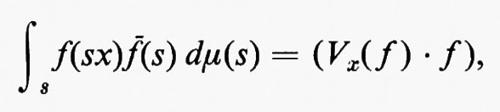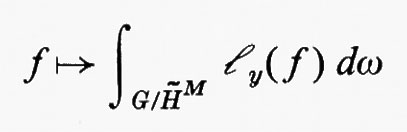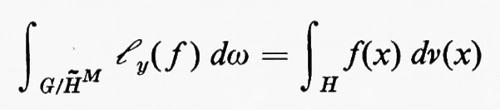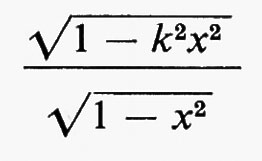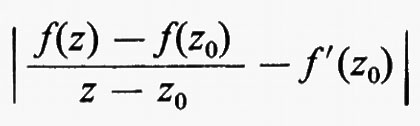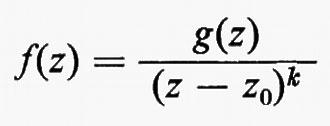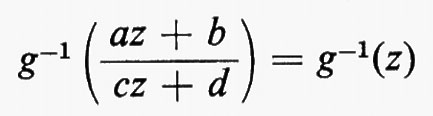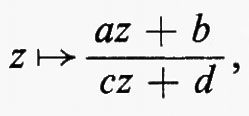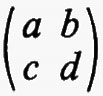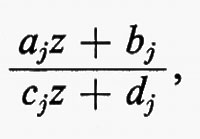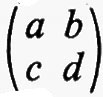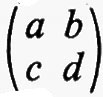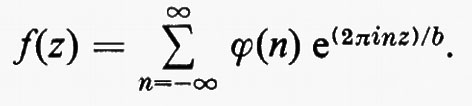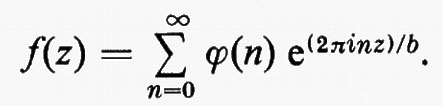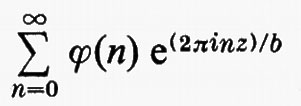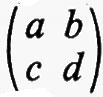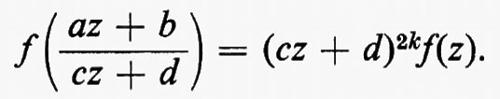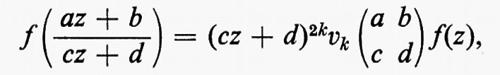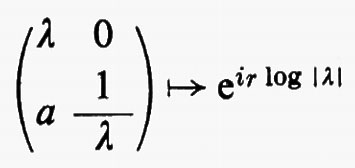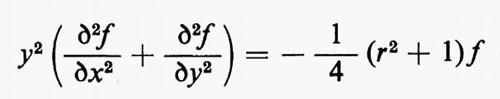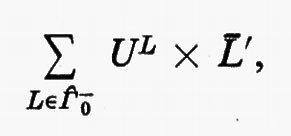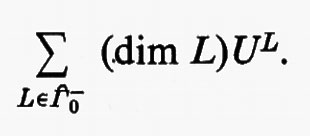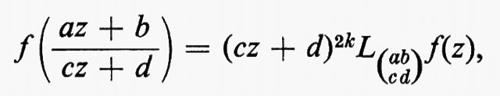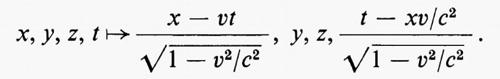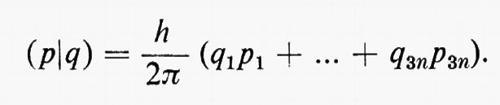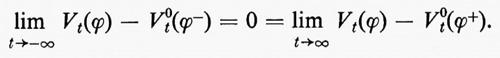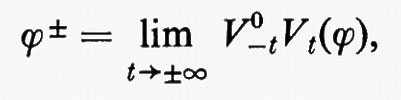Gruppi
Gruppi
di George W. Mackey
SOMMARIO: 1. Introduzione e storia. □ 2. Concetti fondamentali. □ 3. Anelli di endomorfismi e gruppi lineari. □ 4. La struttura dei gruppi finiti. □ 5. Gruppi topologici e gruppi di Lie. □ 6. La struttura delle algebre di Lie e dei gruppi di Lie connessi. □ 7. Rappresentazioni, caratteri e dualità per gruppi finiti. □ 8. Misura di Haar e rappresentazioni unitarie di gruppi separabili localmente compatti in uno spazio di Hilbert. □ 9. Gruppi algebrici. □ 10. Estensioni di gruppi e coomologia di un gruppo. □ 11. Gruppi non discreti di trasformazioni: sistemi dinamici e teoria ergodica. □ 12. Teoria dei gruppi e topologia. □ 13. Teoria dei gruppi e teoria dei numeri. □ 14. Teoria dei gruppi e analisi armonica. □ 15. Teoria dei gruppi e teoria delle funzioni di una variabile complessa. □ 16. Teoria dei gruppi e fisica. □ 17. Considerazioni generali. □ Bibliografia.
1. Introduzione e storia.
I tre simboli, a, b, c, possono essere permutati fra loro in sei modi diversi, contando fra questi la permutazione banale che lascia fermo ciascun simbolo. Queste permutazioni possono venire indicate con (a) (b) (c), (ab)(c), (ac) (b), (bc)(a), (abc) e (bac), ove (abc) è la permutazione che manda a in b, b in c, c in a; (ab)(c) scambia a e b e lascia c fermo, ecc. A partire da due di queste permutazioni si può costruirne una terza facendo seguire una di esse all'altra. Per esempio, (ab)(c) seguito da (bc)(a) manda c in b, b in a e a in c, ed è quindi la permutazione (cba) = (bac). Si dice che (bac) è il ‛prodotto' di (bc)(a) e (ab)(c), e si scrive (bac) = (bc)a (ab)c. In modo simile si può procedere con un qualsiasi insieme finito di simboli o entità matematiche. Per esempio, (a1a6a3a2)(a4a7)(a5)(a8a9) indica la permutazione dei 9 simboli a1~..., a9 che manda a1 in a6, a6 in a3, a3 in a2, a2 in a1, scambia a4 e a7, ecc. Ciascuna coppia di permutazioni di questi simboli ha un prodotto ben definito. In questo caso, ovviamente, questi prodotti sono 9.8.7.6.5.4.3.2 permutazioni distinte, troppe per essere specificate in un tempo ragionevole. Consideriamo le quattro permutazioni (ab)(cd), (ac)(bd), (ad)(bc), (a) (b) (c) (d). Si verifica facilmente che (ab)(cd)•(ac)(bd) = (ad)(bc) e, più in generale, che il prodotto di due qualsiasi di queste permutazioni è ancora una delle quattro. Si dice che queste permutazioni costituiscono un ‛gruppo di ordine quattro' e, più in generale, che una famiglia di permutazioni è un ‛gruppo di permutazioni', o semplicemente un ‛gruppo', se contiene il prodotto di due suoi elementi qualsiasi.
Come nell'algebra ordinaria, useremo il simbolo pn per indicare il prodotto della permutazione p con se stessa n volte. Si rileva facilmente che, presa una qualsiasi permutazione p di un insieme finito, pn deve essere uguale all'identità, e, per un opportuno intero positivo n. Pertanto, p•pn-1 = p = e, e pn-1 è l'unica permutazione q tale che pq = qp = e. Tale permutazione viene chiamata l'inversa di p e viene indicata con il simbolo p-1. Dal momento che p-1 = pn-1, è chiaro che un gruppo di permutazioni di un insieme finito contiene necessariamente l'inverso di ogni suo elemento.
Pur potendosi considerare permutazioni d'insiemi infiniti, il termine permutazione non è tuttavia di uso comune in questo caso. Si parla invece di bigezioni o di trasformazioni biunivoche dell'insieme su se stesso. Naturalmente non è più possibile, in questo caso, descrivere la trasformazione elencando tutti gli elementi e i loro trasformati. Deve esistere una regola o una legge che assegni un elemento T(a) a ogni a appartenente all'insieme infinito A, in modo che ogni a1 sia un T(a) per qualche a e che T(a1) e T(a2) siano distinti ogniqualvolta a1 e a2 siano distinti. Per esempio, se A è l'insieme di tutti i numeri reali, la regola T(a) = a + 7 gode di queste proprietà, così come la regola T1(a) = 5a. Il prodotto T1T di queste due regole o trasformazioni è la trasformazione T2 definita dalla regola T2(a) = 5a + 35. Nel caso infinito, non è più vero che Tn debba essere la trasformazione identica per qualche intero positivo n, e neppure che una famiglia di bigezioni che contenga il prodotto di due dei suoi elementi debba necessariamente contenere l'inverso di ciascun membro. Per esempio, se Tj(a) = a + j, la famiglia costituita da T1, T2, T3, ... contiene il prodotto di due qualsiasi dei suoi elementi, in quanto Tj•Tk = Tj+k, ma non contiene gli inversi, poiché Tj,-1 = T-j. La condizione che T-1 appartenga alla famiglia ogniqualvolta ciò accade per T deve essere imposta separatamente, e, nel caso generale, si dice che una famiglia di trasformazioni bigettive è un gruppo se, e soltanto se, contiene l'inverso di ciascuno dei suoi elementi e il prodotto di due qualsiasi di essi.
La grande importanza della teoria dei gruppi in matematica e in fisica è in parte dovuta alle seguenti circostanze. Molti dei sistemi che vengono studiati contengono un grado minore o maggiore di simmetria, nel senso che le relazioni oggetto di studio vengono lasciate invariate da certe trasformazioni biunivoche degli elementi del sistema stesso. Per esempio, un quadrato nel piano è simmetrico relativamente a rotazioni di multipli interi di 90° intorno al suo centro, a riflessioni rispetto alle diagonali e rispetto alle rette che tagliano per metà due lati opposti. In ogni caso, la famiglia di tutte queste simmetrie costituisce un gruppo di trasformazioni e l'analisi della ‛struttura' di questo gruppo risulta sovente uno strumento prezioso per la comprensione delle proprietà e della struttura del sistema stesso. Può infatti addirittura accadere che tutte le proprietà di un'entità matematica complessa siano implicite nella struttura del suo gruppo di simmetria.
La potenza di questo metodo di analisi è stata per la prima volta riconosciuta in relazione alla teoria della risoluzione di equazioni algebriche mediante radicali. Nel 1770, G. L. Lagrange pubblicò una lunga memoria, nella quale sottopose a una profonda analisi i metodi conosciuti per la risoluzione di equazioni di terzo e di quarto grado. Egli scoprì che è possibile comprendere e unificare questi metodi considerando ciò che accade a varie combinazioni razionali delle radici di un'equazione, quando si permutino queste radici fra di loro. Ciò lo condusse di fatto a stabilire casi particolari di alcuni teoremi elementari sui gruppi finiti. Inoltre, questo suo lavoro suggerì che forse la generica equazione di quinto grado non è risolubile mediante radicali. Questa impossibilità fu provata indipendentemente da P. Ruffini (1813) e N. H. Abel (1824).
Il passo decisivo tuttavia fu compiuto da E. Galois nel 1831. Sia a0 + a1x ... + anxn un polinomio a coefficienti razionali che non può essere fattorizzato come prodotto dì polinomi dello stesso tipo e di grado inferiore. Siano x1, x2, ..., xn i numeri complessi che sono le soluzioni (radici) dell'equazione a0 + a1xn + ... + anxn = 0. Galois introdusse il gruppo G di tutte le permutazioni di x1, x2, ..., xn che lasciano inalterate tutte le equazioni polinomiali in più variabili a coefficienti razionali che possono essere soddisfatte da queste radici. Dipendentemente dall'equazione, questo gruppo può contenere oppure no tutte le possibili permutazioni di n simboli. Galois mostrò che la possibilità di esprimere le xj mediante radicali nelle ak e in numeri razionali dipende solamente dall'esistenza in G di una catena discendente G1 ⊃ Gx ... ⊃ Gn di gruppi più piccoli aventi certe proprietà (chiariremo più avanti la natura di queste proprietà). Si verifica facilmente che una tale catena di gruppi di permutazioni esiste per ogni gruppo di permutazioni di due, tre, o quattro elementi, ma che, per n maggiore di quattro, tale catena non esiste per il gruppo di tutte le permutazioni di n simboli. Non essendo difficile costruire, per ogni n, una equazione il cui gruppo di Galois G sia il gruppo di tutte le permutazioni di x1, ..., xn apparve chiaro perché fosse sempre possibile risolvere per radicali equazioni di grado minore o uguale a quattro, ma che tale possibilità si presentasse solo in casi speciali per equazioni di grado più elevato. Nel corso di questo suo lavoro, Galois introdusse il concetto centrale di ‛sottogruppo normale' (ne vedremo in seguito la definizione). Egli fu anche il primo a usare il termine gruppo.
Il primo a considerare i gruppi finiti di permutazioni, indipendentemente dalle loro applicazioni, pare sia stato A.-L. Cauchy. Egli compì una ricerca dettagliata, cercando di farne una classificazione, fin dal 1815 e ritornò sull'argomento con altri risultati nel 1844-1846.
Il primo libro interamente dedicato alla teoria dei gruppi fu il Traité des substitutions et des équations algébriques di C. Jordan, che apparve nel 1870, mentre la prima esposizione sistematica dell'argomento era apparsa quattro anni prima come parte della terza edizione del Cours d'algèbre supérieure di J.-A. Serret. L'anno 1870, che segue di un secolo la comparsa della memoria fondamentale di Lagrange, è una data significativa nello sviluppo della teoria dei gruppi. Soltanto dopo la pubblicazione del trattato di Jordan cominciarono a diffondersi ampiamente la teoria dei gruppi in generale e le idee di Galois in particolare. Nuovi importanti sviluppi che ampliarono notevolmente l'ambito della teoria seguirono di poco tale data. Alla fine del XIX secolo, il trattato di Jordan, che al suo apparire comprendeva gran parte della teoria, era divenuto un'esposizione sorpassata di una piccola parte di un argomento divenuto nel frattempo assai più vasto. Nel 1870, uomini del valore di L. Kronecker, R. Dedekind e Ch. Hermite avevano sviluppato le idee di Galois sulla relazione tra equazioni algebriche e gruppi di permutazioni delle loro radici, e le avevano sistematizzate in una dottrina che era andata molto al di là dei criteri di Galois sulla risolubilità per radicali. In particolare, essi studiarono equazioni aventi come coefficienti dei polinomi, e giunsero così a un insieme di bellissime relazioni tra le funzioni trascendenti dell'analisi e la soluzione di equazioni algebriche. Nel 1870, tuttavia, la teoria dei gruppi era ancora la teoria dei gruppi finiti di permutazioni e la sua sola applicazione significativa era la classificazione delle irrazionalità delle equazioni algebriche.
Il fatto nuovo, forse più importante, fu la creazione della teoria dei gruppi continui di trasformazioni compiuta da S. Lie in quindici anni, a partire dal 1869. Lie voleva fare per le equazioni differenziali (sia ordinarie che a derivate parziali) quello che aveva fatto Galois per le equazioni algebriche. Egli trovò lo strumento appropriato nel gruppo di tutte le bigezioni del continuo, sul quale la bigezione è definita, che rispettano la differenziabilità e mutano l'equazione (o le equazioni) in se stessa. Per esempio, l'equazione differenziale dy/dx = (x2 + y2)/y2 ha come gruppo d'invarianza il gruppo a un parametro di tutte le trasformazioni del tipo x, y ???14??? tx, ove t è un numero reale positivo. Lo studio del gruppo d'invarianza gettò infatti una nuova luce sul problema dell'integrazione delle equazioni differenziali. Inoltre questi gruppi continui risultarono estremamente interessanti in se stessi e offrirono molte altre applicazioni. In collaborazione con Fr. Engel, Lie riunì la sua opera e quella di altri nel trattato in tre volumi Theorie der Transformationsgruppen, l'ultimo volume del quale apparve nel 1893.
Un altro evento di rilievo, nel periodo successivo al 1870, fu una lezione fatta da F. Klein nel 1872 quando assunse la cattedra di professore a Erlangen. In questa lezione egli enunciò il famoso Erlangen Program volto a unificare la geometria mediante la teoria dei gruppi. Un importante capitolo della matematica è la geometria proiettiva, sviluppata intorno alla metà del XIX secolo in seguito alla pubblicazione del trattato di J. V. Poncelet nel 1822. La geometria proiettiva studia le proprietà delle configurazioni geometriche che restano invariate quando si applichino certe trasformazioni più generali di quelle che conservano la distanza. Da questo punto di vista, cerchi di raggio diverso sono ‛congruenti' sia l'uno all'altro, sia a ellissi e iperboli di tutte le possibili forme. L'insieme di tutte le trasformazioni biunivoche dello spazio che conservano le proprietà proiettive è un gruppo: il gruppo di simmetria della geometria proiettiva. Questo gruppo è molto più ampio del gruppo di simmetria che conserva la distanza, della classica geometria euclidea. L'idea di Klein era quella di studiare la geometria euclidea, quella proiettiva e varie altre geometrie che erano state o avrebbero potuto essere introdotte, collegando le loro proprietà a quelle dei loro gruppi di simmetria, e di considerare le relazioni d'inclusione tra queste geometrie, definite in parte dalle relazioni d'inclusione tra i rispettivi gruppi di simmetria. In particolare, egli suggerì che ogni gruppo di bigezioni di uno spazio definisse una possibile geometria che avrebbe potuto valere la pena di studiare. Klein era per temperamento un organizzatore e un sistematizzatore, ed era anche dotato di uno spirito ‛missionario'. Egli divenne estremamente influente nel mondo matematico e si diede molto da fare per stimolare lo studio dei gruppi e l'introduzione del punto di vista della teoria dei gruppi.
Mentre avvenivano questi importanti sviluppi nell'ambito e nel dominio delle applicazioni della teoria dei gruppi, la vecchia teoria dei gruppi finiti continuava a essere coltivata e la teoria della struttura relativamente superficiale esistente nel 1870 cominciava ad approfondirsi. Particolarmente stimolante fu un importante lavoro di P.L.M. Sylow apparso nel 1872, che conteneva i celebri e insostituibili teoremi di Sylow sull'esistenza dei sottogruppi aventi per ordini delle potenze di numeri primi (si veda più avanti per i dettagli). I progressi nel campo dei gruppi finiti, realizzati nell'ultimo scorcio del XIX secolo, vennero successivamente esposti nel trattato Substitutions Theorie und ihre Anwendung auf die Algebra pubblicato da E. Netto nel 1882, nei due volumi di H. Weber Lehrbuch der Algebra (1895 e 1896) e infine nel trattato di T. W. Burnside del 1897 Theory of groups of finite order.
I gruppi di simmetria delle geometrie più interessanti, come i gruppi di trasformazioni generali studiati da Lie, non solo erano infiniti, ma contenevano elementi che riempivano una varietà continua. Esempio tipico è il gruppo delle trasformazioni del piano complesso esteso, della forma z ???14??? (az + b)/(cz + d), ove a, b, c e d sono numeri complessi arbitrari tali che ad − bc = 1. Si può anche considerare una classe intermedia di gruppi costituita da gruppi che sono infiniti come quelli continui e discreti come quelli finiti. Per esempio, nel gruppo continuo che abbiamo indicato più sopra, si possono considerare soltanto quelle trasformazioni per le quali a, b, c e d sono interi. Nel 1880, con lo sviluppo della teoria delle funzioni automorfe a opera di Klein e di J.-H. Poincaré, apparve l'importanza dei gruppi discreti. Siano ω1 e ω2 due numeri complessi diversi da zero, il cui rapporto non sia reale. Sia Γ il gruppo infinito discreto di tutte le trasformazioni del piano complesso in se stesso della forma z ???14??? n1ω1 + n2ω2, ove n1 e n2 sono interi arbitrari. Affermare che una funzione f della variabile complessa z è doppiamente periodica con periodi ω1 e ω2 vuol dire che f(z + ω1) = f(z + ω2) ≡ f(z), o, equivalentemente, che f(T(z)) = f(z) per ogni T ∈ Γ, cioè che f è lasciata inalterata da ogni trasformazione in Γ. Le funzioni di una variabile complessa, analitiche a eccezione di ‛poli' isolati e doppiamente periodiche, si chiamano funzioni ellittiche. Esse sono le funzioni inverse delle funzioni definite da integrali ellittici, ed erano state introdotte cinquanta anni prima da Abel e K. G. J. Jacobi quale importante strumento per lo studio di questi integrali. Le funzioni automorfe sono simili alle funzioni ellittiche, nel senso che sono analitiche a eccezione di poli isolati e vengono lasciate invariate da un gruppo discreto di trasformazioni. La differenza sta nel fatto che questo gruppo è un gruppo di trasformazioni lineari frazionarie z ???14??? (az + b)/(cz + d), che non consiste soltanto di traslazioni. Inoltre, nel caso più interessante, le funzioni sono definite soltanto in un semipiano. Queste funzioni nacquero quando si vollero costruire le funzioni inverse di soluzioni di equazioni differenziali, ma dimostrarono ben presto di essere di fondamentale importanza nella teoria generale delle superfici di Riemann. In particolare, molte questioni sulle funzioni analitiche e sulle loro superfici di Riemann possono essere riformulate come problemi sui gruppi discreti di trasformazioni lineari frazionarie.
Nel volgere di pochi anni, i gruppi infiniti discreti acquistarono importanza in una direzione d'indagine del tutto diversa. In un solido cristallino gli atomi sono situati nello spazio in un reticolo regolare in modo che la loro configurazione possa essere ‛ripetuta' infinite volte. Se immaginiamo di eseguire una dopo l'altra queste infinite ripetizioni, otteniamo una figura che sarà lasciata invariata da un gruppo infinito discreto di traslazioni spaziali e anche - nella maggior parte dei casi - da certe rotazioni e da altre trasformazioni bigettive che conservano le distanze. L'insieme di tutte queste trasformazioni è un gruppo discreto infinito. La classificazione dei cristalli, secondo le proprietà di questi ‛gruppi spaziali' a essi associati, servì a illuminare i lavori antecedenti dei cristallografi. Una classificazione completa di tutti i possibili gruppi di questo tipo fu fatta indipendentemente da Federov nel 1885-1890, Schoenflies nel 1887-1891 e da Barlow nel 1894, dopo che il problema era stato affrontato in modo incompleto da Sohncke nel 1879 sulla base di certi risultati di Jordan del 1869. È interessante osservare che, se lo spazio fosse ‛non euclideo' nel senso di N. J. Lobačevskij, il problema di determinare i gruppi spaziali sarebbe molto più difficile e - dal punto di vista matematico - equivalente a quello di trovare i possibili gruppi infiniti discreti di trasformazioni lineari frazionane.
Sul finire del XIX secolo venne introdotto nella teoria dei gruppi finiti un nuovo strumento che si sarebbe in seguito dimostrato fondamentale per gli ulteriori sviluppi. Questo strumento è la teoria dei caratteri di un gruppo, o, più o meno equivalentemente, la teoria delle ‛rappresentazioni' dei gruppi mediante gruppi di matrici (o trasformazioni lineari). Quando il gruppo è commutativo o abeliano, nel senso che a•b = b•a per ogni coppia di elementi a e b, si definisce ‛carattere' quella funzione χ che associa a ogni elemento a del gruppo un numero complesso χ(a) di modulo uno, in modo che χ(a•b) = χ(a)χ(b), per tutti gli a e b nel gruppo. Questo concetto, così come il termine ‛carattere', venne introdotto da K. F. Gauss nel 1801 nelle sue famose Disquisitiones arithmeticae. Egli tuttavia lo formulò in modo del tutto indipendente dal linguaggio della teoria dei gruppi e addirittura da quello delle funzioni a valori complessi. In successive ricerche di teoria dei numeri, esso andò assumendo un ruolo importante e diventò gradatamente una nozione della teoria dei gruppi, a mano a mano che i matematici acquistavano dimestichezza con questa teoria. I gruppi commutativi finiti hanno una teoria semplice e piuttosto evidente, e i caratteri non ebbero di per sé grande influenza sulla teoria dei gruppi come tale fino a quando G. F. Frobenius, sollecitato dalla sua corrispondenza con Dedekind circa i ‛determinanti di gruppo', giunse a una generalizzazione naturale della nozione di carattere di un gruppo, che rese possibile l'estensione non banale della teoria ai gruppi non commutativi. Frobenius pubblicò i suoi risultati in una serie di lavori a partire dal 1896. Sebbene in un quadro diverso da quello originale di Frobenius, il modo più semplice per descrivere tale generalizzazione è il seguente: definiamo una rappresentazione di un gruppo finito G come una funzione L che associa una matrice n × n ∥ lij(a) a ogni a in G in modo che ∥ lij(ab) ∥ sia la matrice prodotto di ∥ lij(a) ∥ e ∥ lij(b) ∥ per ogni scelta di a e b in G. Definiamo il ‛carattere' della rappresentazione a ???14??? ∥ lij(a) ∥ come la funzione a valori complessi a → l11(a) + l22(a) + ... + lnn(a) = traccia ∥ lij(a) ∥.
Quando n = 1, una rappresentazione coincide con il suo carattere e la definizione si riduce a quella per i gruppi commutativi. La somma di due caratteri è anch'essa un carattere; e un carattere si dice irriducibile se esso non è la somma di due altri caratteri. Un gruppo finito ha soltanto un numero finito di caratteri irriducibili distinti e la loro determinazione esplicita per un gruppo assegnato può essere un problema stimolante. Inoltre le proprietà dei caratteri sono in una relazione così stretta con le proprietà strutturali del gruppo, che molti fra i teoremi più profondi su questi ultimi non hanno fino a ora potuto essere dimostrati senza far ricorso alla teoria dei caratteri. Infine, come vedremo più avanti, i caratteri e le rappresentazioni sostengono un ruolo ancora più importante nelle applicazioni della teoria dei gruppi di quanto non facciano nella teoria stessa. Non è esagerato affermare che, senza caratteri e rappresentazioni, la teoria dei gruppi sarebbe soltanto l'ombra di se stessa. L'ampio trattato di Burnside del 1897 venne scritto troppo presto per poter includere un'esposizione di questo importante argomento. La seconda edizione, tuttavia, pubblicata nel 1911, ne tratta ampiamente e contiene contributi significativi dello stesso Burnside e di I. Schur, un allievo di Frobenius. Benché molti progressi siano stati compiuti dopo il 1911, questa seconda edizione del libro di Burnside costituisce ancora oggi una trattazione assai utile di molti aspetti della teoria dei gruppi finiti.
Un altro evento di grande importanza per la teoria dei gruppi, verificatosi verso la fine del secolo scorso, fu lo studio sistematico, condotto da Poincaré, della topologia algebrica elaborata in una serie di memorie a cominciare dal 1895. Nella prima di queste, Poincaré dimostrò, fra l'altro, come il fatto che una varietà a n dimensioni non sia ‛semplicemente connessa' possa venir misurato, in un certo senso, da un gruppo discreto, il cosiddetto gruppo fondamentale della varietà. Più specificatamente, egli indicò come si possa associare a una data varietà M un'altra varietà semplicemente connessa ???39??? e un gruppo discreto G di bigezioni di ???39??? in modo che M possa venire ottenuta da M come lo spazio di tutte le ‛G-orbite' in ???39???. (Una G-orbita è l'insieme di tutte le G-trasformate di un punto in M). Per quanto concerne tutte le proprietà essenziali, ???39??? e G sono determinati univocamente da M, e il ‛gruppo fondamentale' G (di solito non commutativo) riflette molte delle proprietà topologiche di M. Quest'applicazione alla topologia della teoria dei gruppi infiniti discreti risultò non essere che un punto di partenza. Molti altri metodi vennero scoperti per collegare in modo significativo gruppi a varietà e a spazi topologici più generali e la topologia algebrica moderna dipende in modo essenziale dalla teoria dei gruppi. Naturalmente queste applicazioni hanno a loro volta influito sulla teoria dei gruppi e, negli sviluppi successivi, le relazioni fra questi due campi di ricerca sono divenute molto intricate. Daremo in seguito altri dettagli.
Col progredire del XX secolo, la storia della teoria dei gruppi diviene sempre più complessa e intimamente connessa con la storia di tutta la matematica. Una volta iniziata la ricerca dei gruppi, li si trovano dovunque, e analizzare un problema o una situazione dal punto di vista della teoria dei gruppi si dimostra molto spesso remunerativo. A questo punto interrompiamo l'esposizione storica sistematica. Nel seguito i riferimenti storici saranno una parte puramente incidentale dell'esposizione dei vari aspetti e delle varie applicazioni della teoria dei gruppi.
2. Concetti fondamentali.
Consideriamo il gruppo di permutazioni di tre oggetti costituito da (abc), (acb) e dall'identità (a) (b) (c). Se paragoniamo questo gruppo al gruppo di trasformazioni del piano costituito dalle rotazioni di 120°, 240° e 0°, si osserva che questi due gruppi di trasformazioni, diversi tra loro, si assomigliano per un aspetto importante. Se trascuriamo gli elementi sui quali essi operano e prendiamo in considerazione solo le trasformazioni in se stesse e il modo in cui esse si combinano rispetto alla moltiplicazione, vediamo che esse hanno esattamente la stessa struttura. Più precisamente, abbinando (abc) con 120°, (acb) con 240° e la identità con l'identità, si vede che tra gli elementi di un gruppo e dell'altro esiste una corrispondenza biunivoca tale che pq corrisponde a p′q′ ogniqualvolta p corrisponde a p′ e q corrisponde a q′. Una corrispondenza di questo tipo, quando esiste, prende il nome di ‛isomorfismo' e si dice che i due gruppi di trasformazioni sono isomorfi come ‛gruppi astratti'. Sorge spontaneamente la domanda seguente. Supponiamo di avere un dato insieme G di oggetti e una regola che a ogni coppia di oggetti p, q di G faccia corrispondere un unico elemento p•q di G che chiameremo il loro prodotto. Di quale proprietà deve godere questa regola di composizione perché G sia isomorfo a qualche gruppo di trasformazioni? La risposta non è difficile. Le proprietà necessarie e sufficienti sono le seguenti: a) (p•q)•r deve essere uguale a p•(q•r) per tutti gli elementi p, q e r di G; b) deve esistere in G un elemento tale che ea = ae = a per tutti gli a in G; c) per ogni elemento p in G deve esistere in G un q tale che pq = qp = e. Fatta questa osservazione, un gruppo, e non necessariamente un gruppo di trasformazioni, si può definire come un sistema costituito da un insieme G e da una regola di composizione p, q → q•p che gode delle proprietà a), b) e c) dianzi indicate. Si dimostra facilmente che l'elemento e è unico; esso si chiama l'elemento identità di G. Allo stesso modo l'elemento q in c) è univocamente determinato da p. Esso si chiama l'inverso di p e s'indica con il simbolo p-1. Questa impostazione, insieme con la nozione di gruppo astratto, venne introdotta da Cayley nel 1854. Solo molto più tardi tuttavia questi concetti diventarono di dominio comune.
Possiamo ora distinguere due parti nel problema dello studio e della classificazione dei gruppi di trasformazioni. Anzitutto studiare i possibili gruppi astratti (identificando quelli fra loro isomorfi). Successivamente studiare i diversi modi in cui è possibile ‛realizzare' un dato gruppo astratto come gruppo di trasformazioni. Lo studio di questo secondo problema comporta l'esame immediato di parecchi concetti importanti. Sia G un gruppo, e supponiamo data una ‛realizzazione' di G come gruppo di trasformazioni di un certo insieme S. Denotiamo con [s]x l'elemento ottenuto trasformando s mediante la trasformazione che corrisponde all'elemento x di G, cosicché [[s]xy] = [[s]x]y. Dati s1 e s2 in S, è possibile che esista un x in G tale che [s1]x = s2. L'insieme di tutti i punti s2 per i quali un tale x esiste si chiama l'‛orbita' di s1 e si vede facilmente che s1 e s2 hanno la stessa orbita se, e soltanto se, l'uno è nell'orbita dell'altro. Così S diventa naturalmente unione di sotto-insiemi disgiunti, ciascuno dei quali è l'orbita di tutti i suoi punti. Quando l'orbita è una sola si dice che il gruppo di trasformazioni è ‛transitivo', o che G agisce ‛transitivamente' in S. Due diverse realizzazioni dello stesso gruppo come gruppo di trasformazioni possono differire tra loro per il numero delle orbite e in particolare una può essere transitiva e l'altra no. Negli esempi, indicati precedentemente, di un gruppo con tre elementi che agisce in spazi diversi, la prima azione è transitiva mentre la seconda ha un numero infinito di orbite. Due realizzazioni possono tuttavia differire anche in altri modi, e in particolare un gruppo dato può agire transitivamente in modi fondamentalmente diversi. Per esempio, in un'azione, l'elemento x di G per il quale [s1 ]x = s2 può essere unico per tutti gli s1 e s2 e in un'altra azione ci può essere un numero infinito di scelte per x.
Di fatto, il grado di unicità nella scelta di x è suscettibile di un'analisi semplice e tuttavia illuminante che è interessante esaminare dettagliatamente. Per ogni s ∈ S, indichiamo con Hs l'insieme di tutti gli x in G per i quali [s]x = s. Si verifica immediatamente che Hs è un sottogruppo di G nel senso che esso stesso è un gruppo rispetto alla moltiplicazione definita in G. Inoltre [s]x = [s]y se, e soltanto se, [s]xy-1 = s ovvero se, e soltanto se, xy-1 è un elemento di Hs o, equivalentemente, se, e soltanto se, x = hy per qualche h ∈ Hs. Quindi il numero delle soluzioni di [s]x = s′ è lo stesso per tutti gli s′ nell'orbita di s, ed è uguale al numero degli elementi in Hs. Si osservi ora che y appartiene a Hsx se, e soltanto se, sxy = sx, cioè xyx-1 ∈ Hs. Quindi Hsx = x-1Hsx e Hsx è isomorfo a Hs. Naturalmente, affermare l'esistenza di un isomorfismo di Hsx su Hs che si estende a un isomorfismo di G su se stesso corrisponde a un enunciato molto più forte che limitarsi a dire che Hsx e Hs sono isomorfi. Ciò implica che questi due sottogruppi sono immersi in G ‛nello stesso modo'. L'enunciato è ancora più forte se diciamo che questo isomorfismo di G su se stesso ha la forma y ???14??? x-1yx. Si dice allora che i sottogruppi sono ‛coniugati'. Un isomorfismo di un gruppo su se stesso si chiama ‛automorfismo' e un automorfismo della forma y ???14??? x-yx-1 prende il nome di automorfismo ‛interno'. Sottogruppi coniugati sono dunque quei sottogruppi trasformabili uno nell'altro mediante automorfismi ‛interni'. Data nello spazio S un'azione del gruppo G, i sottogruppi Hs si chiamano ‛sottogruppi di isotropia' dell'azione. Dalle osservazioni precedenti segue che tutti i gruppi di isotropia di un s in una data orbita sono mutuamente coniugati, e, di fatto, costituiscono appunto una classe di coniugio di sottogruppi. In particolare, ciascuna azione transitiva è associata esattamente con una classe di coniugio di sottogruppi. Inoltre, si verifica senza nessuna difficoltà che questa classe di coniugio di sottogruppi determina completamente la forma dell'azione. Più precisamente, si può provare il seguente teorema. Supponiamo che G agisca transitivamente tanto su S1 che su S2 e che le due azioni abbiano la stessa classe di coniugio di sottogruppi. Esiste allora un'applicazione biunivoca ϕ di S1 su S2 tale che ϕ[(s)x] = [ϕ(s)]x per tutti gli x in S1 e tutti gli x in G. Si dice che le due azioni sono ‛isomorfe'.
A questo punto si presenta in modo naturale il problema di vedere se ogni classe di coniugio di sottogruppi di un gruppo G appaia come la classe dei sottogruppi di isotropia per una azione transitiva di G. La risposta è affermativa quando si generalizzi la nozione di transitività in guisa tale che alcuni elementi di G possano lasciare fissi tutti gli elementi di S. Sia infatti H un sottogruppo arbitrario di G e, per ogni x in G, denotiamo con Hx l'insieme di tutti gli elementi di G della forma hx, ove h appartiene a H. L'insieme Hx si chiama la ‛classe laterale destra' di H contenente x. Si verifica immediatamente che due classi laterali destre aventi qualche elemento in comune sono identiche, così che le classi laterali destre di H ripartiscono G in sottoinsiemi disgiunti. L'insieme di tutte le classi laterali destre di H si indica col simbolo G/H. Facendo agire G come gruppo di trasformazioni su G/H definendo (Hx)y = H(xy), si verifica immediatamente che l'azione è transitiva e che H è il gruppo d'isotropia della classe laterale destra contenente l'identità e. Naturalmente, se y appartiene a xHx-1 per tutti gli x, allora (Hx)y = Hx per tutti gli x e y definisce la trasformazione banale. Inversamente, se y definisce la trasformazione banale, risulta (Hx)y = Hx per tutti gli x, cosicché xyx-1 ∈ H, per tutti gli x, e y ∈ x-1Hx, per tutti gli x. L'insieme N di tutti gli y siffatti è inoltre un sottogruppo tale che xNx-1 = N per ogni x.
I sottogruppi dotati di queste pioprietà si dicono ‛sottogruppi normali' o ‛sottogruppi invarianti' e hanno un ruolo estremamente importante nella teoria generale. Dal modo in cui N è stato definito discende che due elementi x e y appartengono alla stessa classe laterale destra rispetto a N se, e soltanto se, essi definiscono la ‛stessa' trasformazione di G/N. Quindi, identificando le classi laterali destre rispetto a N con le trasformazioni da esse definite, possiamo fare dello spazio G/N delle classi laterali un gruppo. Questo nuovo gruppo prende il nome di ‛quoziente' di G per N e s'indica con il simbolo G/N. Lo spazio G/N delle classi laterali è dunque un gruppo per ‛tutti' i sottogruppi normali N di G. Se π(x) indica la classe laterale alla quale appartiene x, x ???14??? π(x) è un'applicazione di G su G/N che si comporta come un isomorfismo nel senso che π(xy) = π(x)π(y) per tutti gli x e y in G. Differisce tuttavia da un isomorfismo in quanto non è necessariamente biunivoco. Di fatto esso è ovviamente biunivoco se, e soltanto se, N è il sottogruppo banale costituito solamente dall'identità. Si chiamano ‛omomorfismi' quelle applicazioni x →ϕ(x) di un gruppo G in un altro gruppo G′ tali che ϕ(xy) = ϕ(x)ϕ(y). Chiameremo ‛nucleo' dell'omorfismo l'insieme Kϕ di tutti gli x per i quali ϕ(x) è l'identità; chiameremo ‛rango' (o ‛immagine)' di ϕ l'insieme Rϕ di tutti i ϕ(x). Ovviamente Kϕ e Rϕ sono sottogruppi rispettivamente di G e G′ e Kϕ è un sottogruppo normale di G. È facile verificare che ϕ definisce un isomorfismo tra Rϕ e il gruppo quoziente G/Kϕ. Dunque i sottogruppi normali di un gruppo sono precisamente i nuclei dei suoi omomorfismi in altri gruppi, e i suoi gruppi quozienti sono (a meno di isomorfismi) i ranghi di questi omomorfismi.
Se il gruppo G ha un sottogruppo normale N, è in molti casi possibile ricondurre i problemi riguardanti G a problemi relativi a N e al gruppo quoziente G/N. Nella misura in cui ciò è vero, si può pensare che G sia stato ‛scomposto nei fattori' più semplici N e G/N. È quindi importante, quando si analizza la struttura di un gruppo G, conoscere i suoi sottogruppi normali. Un gruppo che non ha sottogruppi normali eccetto se stesso e l'identità, e non è quindi suscettibile di questo tipo di analisi, si chiama ‛semplice'. Per i gruppi finiti, e in misura considerevole anche per altri gruppi, il problema di trovare tutte le classi di isomorfismo dei gruppi si può ridurre ai due seguenti problemi: 1) determinare i gruppi semplici; 2) per ogni coppia di gruppi N e Q, trovare il gruppo più generale G avente un sottogruppo normale N0 isomorfo a N, tale che G/N0 sia isomorfo a Q. Il problema 2) si chiama ‛problema di estensione di un gruppo'. Le soluzioni si dividono naturalmente in due classi a seconda che in G esista oppure no un secondo sottogruppo Q0 tale che Q0 e N0 abbiano in comune soltanto l'identità e tale che ogni elemento di G sia un prodotto di un elemento di Q0 e di un elemento di N0. Se Q0 esiste, esso è necessariamente isomorfo a G/N0. In questo caso si dice che l'estensione ‛si spezza'. Lo studio delle estensioni di questo tipo equivale allo studio dei possibili omomorfismi di Q nel gruppo degli automorfismi di N. Possiamo infatti scrivere in modo univoco ogni elemento di G nella forma nq con n ∈ N, q ∈ Q0. Poiché inoltre (n1q1)(n2q2) = n1(q1n2q1-1)q1q2, la moltiplicazione in G è determinata quando sia nota la moltiplicazione in N0 e in Q0 e, per ogni q ∈ Q0, l'automorfismo n ???14??? qnq-1. Reciprocamente, dati i gruppi N e Q, indichiamo con G l'insieme di tutte le coppie n e q, con n in N e q in Q, e supponiamo che q → αq faccia corrispondere un automorfismo di N a ogni q in Q. Si definisca una moltiplicazione in G ponendo (n1q1)(n2q2) = n1αq1(n2)q1q2. Un calcolo diretto mostra che G soddisfa gli assiomi di gruppo se, e soltanto se, q → αq è un isomorfismo. Si dice allora che il gruppo G è un ‛prodotto semidiretto' di N e Q. Esiste sempre almeno un omomorfismo q ???14??? αq: quello per cui αq(n) = n per ogni q e ogni n. In questo caso la moltiplicazione diviene (n1q1)(n2q2) = n1n2q1q2, N e Q sostengono ruoli simmetrici e G prende il nome di ‛prodotto diretto' di N e Q: G = N × Q. Più in generale, mediante una banale estensione della regola precedente, si può definire il prodotto diretto di una famiglia finita o infinita di gruppi {Gn}. Lo studio delle estensioni che non sono del tipo precedente è più complicato e conduce alla teoria della coomologia dei gruppi, a proposito della quale rinviamo al cap. 10 per maggiori dettagli.
Così come si possono considerare prodotti diretti di più di due gruppi, allo stesso modo si possono considerare estensioni successive di un gruppo. In altre parole, un sottogruppo normale N1 di un gruppo può avere esso pure un sottogruppo normale N2 (non necessariamente normale in G); N2 può avere un sottogruppo normale N3 ecc., e si possono formare i gruppi quozienti G/N1, N1/N2 , N2/N8, ... . Una siffatta successione di sottogruppi G ⊃ N1 ⊃ N2 ... Nγ = {e} si chiama una ‛serie normale' e i suoi quozienti G/N1, N1/N2, ... si chiamano i suoi fattori. Se il gruppo G è finito, si possono ovviamente scegliere gli Nj in modo che tutti i fattori siano semplici. Nel caso generale ciò può anche rivelarsi impossibile. Se una scelta siffatta è possibile, la serie normale che ne risulta si chiama ‛serie di composizione'. Benché un gruppo possa avere molte serie di composizione distinte, due qualsiasi di esse sono simili, nel senso che i fattori corrispondenti sono gli stessi a meno di isomorfismi e cambiamenti d'ordine. In altre parole, se G = N0 ⊃ N1 ⊃ N2 ... ⊃ Ms = {e} sono serie di composizione per lo stesso gruppo G, risulta γ = s ed esiste una permutazione π degli interi 1, 2, ..., γ tale che Nj-1/Nj è isomorfo a Mπ(j)-1/Mπ(j) per j = 1, 2, ..., γ. Questo risultato sorprendente si deve a Jordan e L. O. Hölder. Esso implica in particolare che ogni gruppo finito è associato in modo invariante a una famiglia di classi di isomorfismo di gruppi semplici. Si dice che un gruppo finito è ‛risolubile' se i fattori di una sua serie di composizione sono tutti commutativi. Questa terminologia risale a Galois, in relazione al fatto che un'equazione è risolubile mediante radicali se essa ammette una serie normale i cui fattori sono tutti commutativi; vale a dire se può essere costruita a partire da gruppi commutativi, mediante un numero finito di successive estensioni di gruppo.
Se N1 e N2 sono sottogruppi normali del gruppo G, il commutatore [N1, N2] di N1 e N2 è per definizione il più piccolo sottogruppo di G che contiene gli elementi del tipo xy(yx)-1 = xyx-1y-1, al variare di x in N1 e di y in N2. Quando N1 = N2 = G, esso prende il nome di sottogruppo commutatore di G ed è, in senso ovvio, il ‛più piccolo' sottogruppo normale di G il cui quoziente sia commutativo. Posto G1 = [G, G]G(n+1)~ = [G(n), G(n)], si ottiene così una successione di sottogruppi normali, e posto ???40???1 = [G, G], ???40???(n~1) = [G, G(n)], se ne ottiene un'altra. Si vede facilmente che G è risolubile se, e soltanto se, G(n) si riduce all'identità per qualche n, e allora G, G1, ..., G(n) è una serie canonica normale con fattori commutativi. Se ???40???(n) si riduce all'identità per qualche n, si dice che G è ‛nilpotente'. I gruppi nilpotenti sono risolubili, ma non vale l'inverso. L'insieme di tutti gli x in G tale che xy = yx, per tutti gli y in G, è un sottogruppo normale commutativo che si chiama il centro di G. e G è nilpotente e n è il più piccolo intero positivo per il quale ???40???(n) = {e}, ???40???(n-1) deve stare nel centro. Così i gruppi nilpotenti hanno sempre centri non banali. Definiamo una successione Z1, Z2, ... di sottogruppi normali di un gruppo arbitrario G prendendo come Z1 il centro di G e come Zn+1 l'insieme di tutti gli x la cui immagine in G/Zn stia nel centro di G/Zn. Non è difficile dimostrare che G è nilpotente se, e soltanto se, Zn = G per un certo n.
3. Anelli di endomorfismi e gruppi lineari.
Un omomorfismo di un gruppo commutativo in se stesso si chiama ‛endomorfismo'. Se α e β sono endomorfismi dello stesso gruppo commutativo V, definiamo α + β come l'applicazione di V in V che porta v in a(v) + β(v). Non è difficile verificare che anche α + β è un endomorfismo di V e che l'insieme R(V) di tutti gli endomorfismi di V è anch'esso un gruppo commutativo rispetto all'operazione a, β → α+β. L'identità di questo gruppo s'indica con O ed è l'endomorfismo che applica ogni elemento di V nell'identità di V. L'inverso di α s'indica con −α ed è l'endomorfismo v a(v-1). Vediamo ora come gli endomorfismi possano essere ‛moltiplicati' oltre che sommati, il ‛prodotto' di α e β essendo per definizione l'endomorfismo v → α(β(v)) = αβ(v) ottenuto componendo α e β. L'operazione α, β → αβ non è in generale commutativa, ma chiaramente soddisfa sia la legge associativa (αβ)γ = α(βγ) sia quella distributiva α(β+γ) = αβ + αγ, e (β + γ)α = βα + γα. Un sottoinsieme A di R(V) che contenga α + β, −α, −β, e αβ, ogniqualvolta contenga α e β, si chiama ‛anello di endomorfismi'. Reciprocamente, sia R un qualsiasi insieme in cui siano state definite due operazioni: α, β → α + β e α, β →αβ. L'insieme R è isomorfo (nel senso ovvio) a un anello di endomorfismi se, e soltanto se, R è un gruppo commutativo rispetto a + e soddisfa le leggi distributiva e associativa descritte più sopra. Si ha una nozione corrispondente di anelli astratti e la relazione fra anelli astratti e anelli di endomorfismi è perfettamente analoga a quella fra gruppi astratti e gruppi di trasformazioni. Se gli elementi distinti da 0 di un anello formano un gruppo rispetto all'operazione α, β → αβ l'anello si chiama ‛anello con divisione' e, se questo gruppo è commutativo, l'anello con divisione si chiama ‛corpo'. L'esempio più familiare di corpo è quello dell'insieme di tutti i numeri razionali m/n, con m e n interi e n ≠ 0. Esso è un corpo rispetto all'addizione e alla moltiplicazione ordinaria. Altri esempi sono il corpo dei numeri reali e quello dei numeri complessi. Esistono anche corpi che hanno soltanto un numero finito di elementi. Gli esempi più semplici sono gli anelli di endomorfismi di gruppi ciclici di ordine primo. Un gruppo si dice ‛ciclico' se contiene un ‛generatore', cioè un elemento x tale che ogni elemento del gruppo è xn o (x-1)n per qualche intero finito n. Se xn = e, per qualche intero positivo n, e se n è il più piccolo intero non negativo per cui ciò succede, il gruppo contiene allora soltanto x, x2, ..., nn, e si dice di ‛ordine' n. Per ogni intero positivo finito n esiste soltanto un gruppo ciclico di ordine n, definito a meno di isomorfismi. Il gruppo degli interi rispetto all'addizione è un gruppo ciclico infinito che ha come gruppi quozienti tutti i possibili gruppi ciclici finiti. Chiaramente i gruppi semplici commutativi sono tutti ciclici e si vede facilmente che un gruppo ciclico finito è semplice se, e soltanto se, il suo ordine è primo. Si dimostra in modo ovvio che l'anello degli endomorfismi di un gruppo ciclico di ordine primo p è un corpo e contiene p elementi. Si può dimostrare che due corpi finiti sono isomorfi se, e soltanto se, essi hanno lo stesso ordine (numero di elementi) e che gli ordini possibili sono proprio le potenze prime pn. Poiché si può dimostrare che un anello finito con divisione è necessariamente un corpo, anche gli anelli finiti con divisione sono tutti noti.
Sia F un corpo qualsiasi e sia n un intero positivo. Per matrice n × n s'intende una funzione a la quale assegna un elemento aij di F a ogni coppia d'interi i j con l ≤ i ≤ n e l ≤ j ≤ n. Due qualsiasi matrici n × n, a e b, sul medesimo corpo F hanno una somma a + b definita mediante la regola (a + b)ij = aij + bij e un prodotto ab definito dalla
e, rispetto a queste operazioni, l'insieme di tutte le matrici n × n su F forma un anello. Questo anello si può realizzare in modo naturale come un anello di endomorfismi del prodotto diretto di n copie del gruppo additivo di F (cioè del gruppo commutativo che si ottiene da F quando si consideri soltanto l'operazione di addizione). Si dice che un anello arbitrario R ha un'identità quando esiste un elemento 1 tale che a1 = 1a per tutti gli a in R. L'identità - 1 se esiste - è chiaramente unica. Se R è un anello con identità si dice che un elemento a ha un ‛inverso', se esiste un elemento b tale che ab = ba = 1. L'elemento b - quando esiste - è unico e si indica con a-1. È chiaro che l'insieme di tutti gli elementi che hanno un inverso è un gruppo rispetto alla moltiplicazione. La matrice a, tale che aij = 0 per i ≠ j e aii = 1 per i = 1, 2, ..., n, è un'identità per l'anello delle matrici n × n su F e le matrici che hanno un inverso si chiamano ‛matrici non singolari'. Per ciascun F e n, il gruppo di tutte le matrici n × n non singolari si indica con il simbolo GL(n, F) e ci si riferisce ad esso come al ‛gruppo lineare generale'.
Per definizione, il determinante di una matrice 2 × 2 è a11a22 − a12a21 e il determinante di una matrice 3 × 3 è a11(a22a33 − a32a23) − a12(a21a33 − a23a81) + a13(a21a32 − a22a31). Più in generale, si definisce per ricorrenza il determinante det. a di una matrice n × n come segue: det. a = a11D11 − a12D12 ... ± a1n~D1n~ ove D1j~ è il determinante della matrice (n − 1) × (n − 1), b1j~, i cui elementi sono: b¹jjk = ai+1,k, se k 〈 j e b¹ink = a+1,k+1, se k ≥ j. Si dimostra che a non è singolare se, e soltanto se, det. a ≠ O e che det. (ab) = det. a det. b per tutte le matrici a e b. Pertanto a ???14??? det. a è un omomorfismo di GL(n, F) nel gruppo moltiplicativo di F. Il nucleo dell'omomorfismo è un sottogruppo normale di GL(n, F) che si indica con SL(n, F). Il centro di GL(n, F) consiste di tutte le matrici a tali che aii = ajj ≠ 0 e aij = 0 per i ≠ j. Esso è un sottogruppo normale, isomorfo al gruppo moltiplicativo di F. Il quoziente di GL(n, F) per il centro si chiama ‛gruppo proietti- vo' e si indica con il simbolo PGL(n, F). Il centro di SL(n, F) è costituito da quelle matrici tali che aij = 0 per i ≠ j e αii = λ per tutti gli i con λn = 1. Il quoziente di SL(n, F) per il suo centro si chiama ‛gruppo proiettivo speciale' e si indica con PSL(n, F). A eccezione di due casi, il gruppo proiettivo speciale è un gruppo semplice ogniqualvolta n ≥ 2 e F è un corpo finito oppure un corpo in cui 1 + 1 ≠ 0. Le due eccezioni sono PSL(2, F) ove F è un corpo finito con due o tre elementi.
Per ogni n e F il gruppo GL(n, F) contiene alcuni sottogruppi particolarmente interessanti e importanti. Si osservi anzitutto che GL(n, F) si può rappresentare come un gruppo di trasformazioni su se stesso ponendo a(q) = aTqa, ove (aT)ij = aji per tutti gli i e j. aT prende il nome di trasposta di a e si dice che a è simmetrica se aT = a e antisimmetrica se aT = −a. Esistono elementi antisimmetrici di GL(n, F) se, e soltanto se, n = 2m, ove m è un intero positivo. Tali elementi, quando esistono, costituiscono esattamente un'orbita nell'azione di GL(n, F) su se stesso dianzi descritta. Per conseguenza, se q1 e q2 sono due qualsiasi elementi antisimmetrici di GL(n, F), il sottogruppo di tutte le a con aTq1a = q1 è coniugato del sottogruppo di tutte le a con aTq2a = q2. Per amore di concretezza, si scelga come q la particolare matrice antisimmetrica tale che q2j+1,2j = −1 e qik~ = 0 per tutte le altre coppie i, k. Il sottogruppo di tutte le a con aTqa = q si chiama in questo caso il ‛gruppo simplettico' e si indica con Sp(m, F). Esso è un sottogruppo di SL(2m, F) e ha un centro che contiene soltanto l'elemento unità e il suo opposto. Il quoziente per questo centro è semplice tranne che in due casi: quando n = 1 e F è il corpo con due o tre elementi e quando n = 2 e F è il corpo con due elementi.
Si può anche considerare il sottogruppo di tutte le a con aTqa = q per una q simmetrica. In questo caso può esserci più di un'orbita e quindi più sottogruppi non coniugati, e persino non isomorfi, per n e F dati. Quando 1 + 1 ≠ 0, questi gruppi prendono il nome di ‛gruppi ortogonali'. Il determinante di un elemento di un gruppo ortogonale è ± 1, ma non necessariamente 1. Il sottogruppo delle matrici con determinante 1 si chiama ‛gruppo ortogonale proprio'. Il quoziente di un gruppo ortogonale proprio per il suo centro è nella maggior parte dei casi un gruppo semplice. Rimandiamo i lettori ai testi che citeremo più avanti (e alla voce algebra) sia per un enunciato preciso che per quanto concerne i gruppi ortogonali nel caso in cui sia 1 + 1 = 0.
Supponiamo ora che il corpo F ammetta un automorfismo non banale a → ā tale che ā = a. In tal caso l'insieme di tutte le a in GL(n, F) con āTa = 1 è un sottogruppo detto ‛gruppo unitario'. Esso dipende ovviamente dall'applicazione a → ā oltre che da n e da F. Il sottogruppo degli elementi di determinante 1 si chiama ‛gruppo unitario speciale'. Come nel caso del gruppo ortogonale proprio, il quoziente del gruppo speciale unitario per il suo centro è - nella maggior parte dei casi - un gruppo semplice.
I gruppi GL(n, F) e i loro sottogruppi simplettici, ortogonali e unitari si chiamano ‛gruppi classici'. I casi particolari di questi gruppi, nei quali F è un corpo finito con un numero primo di elementi, furono oggetto di uno studio esteso e sistematico da parte di Jordan nel suo trattato del 1870. L'estensione al caso in cui F sia un corpo finito arbitrario è dovuta essenzialmente a L. E. Dickson, che la espose dettagliatamente nel suo libro Linear groups del 1901. Dickson si dedicò anche allo studio dei gruppi classici su corpi infiniti, ma lasciò molti problemi insoluti. Il trattato di J. A. Dieudonné Sur les groups classiques del 1948 semplificò il lavoro di Dickson e diede una soluzione a molti problemi di struttura.
4. La struttura dei gruppi finiti.
Il numero degli elementi in un gruppo finito G si chiama ‛ordine' di G e si indica di solito con o(G) oppure con ∣ G ∣. Per ogni intero positivo n, esiste almeno un gruppo di ordine n: il gruppo ciclico di ordine n. Dipendentemente da n, possono esisterne o no degli altri. Sia H un sottogruppo del gruppo finito G. Come abbiamo notato nel cap. 2, le classi laterali destre di H sono disgiunte o identiche e ciascuna ha lo stesso numero di elementi di H. Perciò ∣ G ∣ = ∣ H ∣k, ove k è il numero delle classi laterali distinte Hx. Ne segue che l'ordine di un sottogruppo divide sempre l'ordine del gruppo. Questa dimostrazione venne indicata da Lagrange nel 1770 e il risultato è noto come teorema di Lagrange. Esso implica in particolare che un gruppo il cui ordine è un numero primo non può avere altri sottogruppi che se stesso e l'identità; pertanto esso è ciclico ed è generato da ogni suo elemento distinto dall'identità. Si dimostra facilmente che il prodotto diretto di due gruppi cidici è ciclico se, e soltanto se, gli ordini dei due gruppi non hanno fattori comuni. Esistono quindi almeno due gruppi non isomorfi di ordine 4: uno è ciclico e l'altro è il prodotto diretto di due gruppi ciclici di ordine 2. Si può dimostrare che non ne esistono altri. Naturalmènte i gruppi ciclici sono commutativi, come pure ogni prodotto diretto di gruppi ciclici. Così tutti i gruppi di ordine uguale o inferiore a 5 sono commutativi. Il gruppo non commutativo di ordine più basso è il gruppo di sei elementi costituito da tutte le permutazioni di tre oggetti. Esso ha un sottogruppo normale di ordine 3 e l'estensione si spezza. Si tratta quindi di un prodotto semidiretto di due gruppi ciclici. In generale, se indichiamo con Zn il gruppo ciclico di ordine n, x ???14??? x-1 è un automorfismo di Zn ed è banale soltanto se n = 2. Esso genera un gruppo di automorfismi di ordine 2 e, corrispondentemente, si ha un prodotto semidiretto di Z2 e Zn. Questo prodotto semidiretto è un gruppo non commutativo di ordine 2n e si chiama il gruppo ‛diedrale' di quell'ordine. Si può dimostrare che ogni gruppo di ordine 6 è ciclico oppure è isomorfo al gruppo diedrale di ordine 6.
Il fatto ovvio che ogni prodotto diretto di gruppi commutativi ciclici è commutativo ha un inverso nowbanale. Ogni gruppo commutativo finito è isomorfo a un prodotto diretto di gruppi ciclici. Inoltre è possibile scegliere questi gruppi ciclici in modo che i loro ordini siano potenze di primi; compiute queste scelte, i gruppi commutativi sono determinati unicamente a meno di isomorfismi. Ciò significa che esistono tanti gruppi commutativi non isomorfi di un dato ordine n quanti sono i modi distinti di scomporre n in prodotto di potenze di primi. Per esempio, poiché 8 = 23 = 22 × 2 = 2 × 2 × 2, esistono tre gruppi isomorfi di ordine 8 commutativi: Z8, Z4 × Z2, Z2 × Z2 × Z2. Similmente, i possibili gruppi commutativi di ordine 9, 10, li e 12, sono Z9, Z3 × Z3, Z2 × Z5 = Z10, Z11, Z3 × Z2 × Z2 e Z3 × Z4 = Z12. Il problema di determinare (a meno di isomorfismi) tutti i possibili gruppi commutativi finiti può considerarsi completamente risolto. Quest'analisi risale a Gauss, il quale di fatto trattò nel 1801 un caso speciale del teorema, connesso con le sue ricerche sulle forme quadratiche. La sua dimostrazione tuttavia non venne pubblicata fino al 1863. La trattazione moderna risale al 1870 ed è dovuta a L. Kronecker.
Non è difficile determinare, a meno di isomorfismi, tutti i gruppi (non necessariamente commutativi) di un dato ordine n, purché n sia il prodotto di un numero abbastanza piccolo di fattori primi. Ecco due fra i teoremi più importanti. Se n è il quadrato di un numero primo p, G deve essere commutativo e quindi isomorfo a Zn oppure a Zp × Zp. Se n è il prodotto di 2 e di un numero primo dispari, G è ciclico, oppure è isomorfo al gruppo diedrale di ordine n. I risultati citati più sopra sui gruppi di ordine 4 e 5 sono naturalmente conseguenze di questi teoremi. Tenuto conto del fatto che i gruppi di ordine primo sono ciclici, essi permettono di determinare tutte le classi di isomorfismo dei gruppi di ordine fino a 16, a eccezione dei gruppi di ordine 8, 12 e 15, ai quali provvedono i seguenti teoremi. Se n = 4p, con p primo, e se p − 1 non è divisibile per 4, esiste uno e un solo gruppo di ordine n il quale è un'estensione non spezzata di Z2p e, se p ≠ 3, ogni gruppo non commutativo di ordine n è isomorfo a questa estensione, oppure al gruppo diedrale di ordine n. Quando p = 3, quando croè n = 12, si presenta un'altra possibilità: il caso in cui il gruppo sia il prodotto semidiretto di Z2 × Z2 per il gruppo generato da quegli automorfismi che permutano ciclicamente i tre elementi distinti dall'identità. Se n è il prodotto di due numeri primi p e q, con p 〈 q, G è ciclico, a meno che q − 1 sia un multiplo di p. Se q − 1 è un multiplo di p, il gruppo degli automorfismi di Zq contiene un sottogruppo isomorfo a Zp e ogni gruppo non commutativo di ordine n = pq è isomorfo al corrispondente prodotto semidiretto di Zq e Zp.
Per dimostrare questi teoremi, si fa largo uso del teorema di Sylow al quale abbiamo accennato nell'introduzione e che può considerarsi volto a risolvere parzialmente il seguente problema, posto dal teorema di Lagrange: dato un gruppo G di ordine n, per quale divisore m di n esiste un sottogruppo H di ordine m? Sylow dimostrò che H esiste sempre se m è una potenza di un numero primo; se, inoltre, esso è la più alta potenza di quel numero primo che divide n, H è unico a meno di un coniugio. Dunque, se n1α1p2α2 ... prα2, ove p1, p2, ..., pr sono numeri primi distinti, H ammette un sottogruppo di ordine pjαj(j = 1, ..., r) e questi sottogruppi sono univocamente determinati, a meno di un coniugio. Essi si chiamano i sottogruppi di Sylow di G. Sylow dimostrò anche che ogni sottogruppo avente per ordine la potenza di un numero primo è contenuto in qualche gruppo di Sylow e che il numero dei sottogruppi di Sylow associati a un qualsiasi numero primo dato p supera di un'unità un multiplo di p. Si comprende chiaramente, per i teoremi di Sylow, che la struttura dei gruppi aventi come ordini potenze di numeri primi (p-gruppi) sostiene un ruolo essenziale nello studio dei gruppi finiti in generale. Un fatto elementare importante è che un p-gruppo è sempre nilpotente. Poiché i prodotti diretti di gruppi nilpotenti sono anch'essi nilpotenti, un gruppo non può essere il prodotto diretto dei suoi sottogruppi di Sylow a meno che non sia nilpotente. E possibile di fatto provare che - inversamente - ogni gruppo nilpotente è il prodotto diretto dei suoi sottogruppi di Sylow, cosicché lo studio dei gruppi finiti nilpotenti si riduce allo studio dei p-gruppi.
In una serie di lavori apparsi tra il 1925 e il 1937, Philhp Hall generalizzò nel modo seguente i teoremi di Sylow: supponiamo che l'ordine di un gruppo G sia p1α1 p2α2 ... prαr, ove i pj sono numeri primi distinti. Se G è risolubile, per ogni sottoinsieme pj1, pj2, ..., pjk degli r numeri primi p1, ..., pr esiste un sottogruppo G di ordine pjα1j1 pjα2j2 pjαkjk. Questo sottogruppo è unico a meno di un coniugio. Reciprocamente, se per ogni j esiste un sottogruppo di ordine n/pjαj, G è risolubile. Nel caso particolare in cui r = 2, n/pjαj è esso stesso un numero primo e quindi - in base al teorema di Sylow - il sottogruppo desiderato esiste. Pertanto, ogni gruppo il cui ordine è del tipo p1α1p2α2 è necessariamente risolubile. Questo caso speciale del teorema di Hall fu dimostrato da Burnside nel 1904, usando la teoria dei caratteri. Dopo di allora non si è trovata nessun'altra dimostrazione che non si servisse dei caratteri. Si ricava facilmente dai teoremi di Hall che ogni gruppo G risolubile ammette dei sottogruppi di Sylow S1, S2, ..., Sr tali che ogni elemento x di G sia espresso in modo unico come prodotto y1y2 ... yr, dove yj ∈ Sj.
La conoscenza della struttura dei p-gruppi è abbastanza estesa sia per merito dei primi risultati raccolti nel libro di Burnside che per i contributi di Phillip Hall e di altri. Non è possibile tuttavia esprimere concisamente i risultati.
Nello studio dei gruppi finiti non risolubili, uno dei maggiori problemi consiste nel trovare tutte le possibili classi di isomorfismo di gruppi semplici. Benché il problema non sia definitivamente risolto, tuttavia molti progressi sono stati compiuti a partire dal 1955. Indichiamo con Sn il gruppo di ‛tutte' le permutazioni di n oggetti - il cosiddetto gruppo simmetrico - e chiamiamo ‛trasposizione' una permutazione che scambi due oggetti e lasci fissi gli altri. I prodotti di un numero pari di trasposizioni costituiscono un sottogruppo normale, An, detto gruppo alterno, che non contiene trasposizioni; Sn è il prodotto semidiretto di An e del gruppo di due elementi generato da una qualsiasi trasposizione. Per n ≤ 4 An è uno dei gruppi risolubili descritti più sopra, ma, per n ≤ 5 è possibile dimostrare che esso è semplice. Pertanto gli An per n ≥ 5 costituiscono una serie infinita di gruppi semplici mutuamente non isomorfi. Il gruppo semplice A5 è di ordine 60 ed è il gruppo semplice di ordine più basso. Di fatto è l'unico gruppo non risolubile con meno di 120 elementi. Come abbiamo spiegato più dettagliatamente nel cap 3, altre serie infinite di gruppi semplici finiti possono essere costruite partendo da gruppi classici su corpi finiti. Per esempio, PSL(n, F) è semplice per tutti gli n = 3, 4,..., quando F è il corpo finito di pk elementi, ove p è un numero primo qualsiasi e k è un intero positivo arbitrario. Esso è semplice quando n = 2 e pk ≠ 2 o 3. Enunciati simili, ma molto più complicati, possono trovarsi per i quozienti, rispetto ai loro centri, delle intersezioni degli altri gruppi classici con SL(n, F). Un'analisi completa della situazione, insieme con una lista di tutti i gruppi semplici finiti non commutativi noti nel 1901 è fornita da Dickson nel suo libro Linear groups citato nel cap. 3. Oltre ai quozienti semplici dei gruppi classici e ai gruppi An per n ≥ 5, vi erano 5 gruppi semplici che pareva non facessero parte di nessuna famiglia infinita. Nel 1861 e nel 1873 Mathieu aveva dimostrato l'esistenza di gruppi di permutazioni quintuplamente transitivi su 12 e 24 oggetti, i quali non comprendevano A12 e A24. Essi vengono indicati con M12 e M24 in onore di Mathieu. Il sottogruppo di M12 che lascia fisso un elemento è chiaramente quadruplamente transitivo su 11 oggetti; lo si indica con M11. In modo analogo, vengono definiti, a partire da M24, M23 e M22. Nel 1900, G. A. Miller dimostrò che questi 5 gruppi, noti come i ‛gruppi di Mathieu', sono semplici. Essi sono appunto i 5 gruppi eccezionali della lista di Dickson. In una ricerca iniziata nel 1901, e portata a termine nel 1904, lo stesso Dickson aggiunse una nuova famiglia infinita di gruppi semplici. Per ogni corpo F si può costruire un sottogruppo di SL(7, F) il cui quoziente è semplice. Se F è infinito, i gruppi semplici così ottenuti non sono isomorfi a nessuno dei gruppi semplici noti in precedenza.
Dopo questi studi di Dickson, l'elenco dei gruppi semplici conosciuti restò invariato per mezzo secolo, fino a che, nel 1955, C. Chevalley scoprì un metodo sistematico per costruire parecchie nuove famiglie infinite. Come spiegheremo in un capitolo successivo, i gruppi continui semplici di Lie possono essere classificati completamente e contengono un numero finito di famiglie infinite insieme a un numero finito di gruppi ‛eccezionali'. Quattro di queste famiglie hanno una struttura ‛analitica complessa' e nel loro insieme costituiscopo i gruppi classici sul corpo dei numeri complessi (eccezion fatta per quelli unitari). Fra i gruppi eccezionali, cinque hanno anch'essi una struttura analitica complessa. Chevalley mostrò come si potessero definire gruppi analoghi a tutti i gruppi semplici di Lie dotati di una struttura analitica complessa, partendo da un corpo arbitrario invece che da quello dei numeri complessi. Provò inoltre che, in gran parte dei casi, tali gruppi sono ancora semplici. Quando il corpo è finito, i gruppi semplici corrispondenti sono finiti e per quanto riguarda i gruppi di Lie complessi eccezionali non sono compresi nella lista di Dickson. Quelli definiti dal gruppo eccezionale di dimensione più bassa coincidono con i nuovi gruppi aggiunti da Dickson nel 1901 e nel 1904. Tuttavia, quelli definiti da altri gruppi eccezionali, erano sconosciuti prima di allora. L'indagine di Chevalley venne completata ed estesa da R. Ree, M. Suzuki, R. Steinberg e J. Tits che trovarono così, agli inizi del 1960, altre famiglie infinite di gruppi semplici di Lie. Successivamente, nel 1965, Z. Janko scoprì un nuovo gruppo semplice finito che non appartiene a nessuna famiglia infinita. Le ricerche di Janko furono presto riprese da altri studiosi e nuovi gruppi semplici ‛sporadici' continuano ad apparire a brevi intervalli. Per un'esposizione sistematica di questi risultati aggiornata al 1970, rinviamo il lettore all'articolo di W. Feit pubblicato negli atti del Congresso Internazionale dei Matematici tenuto a Nizza nel 1970.
Poiché tutti i gruppi semplici non commutativi compresi nella lista di Dickson erano di ordine pari, fu naturale congetturare che tutti i gruppi semplici finiti non commutativi fossero di ordine pari, o - equivalentemente - che ogni gruppo di ordine dispari fosse risolubile. Le ricerche relative a tale questione non fecero nessun progresso significativo per più di mezzo secolo, finché - con un lavoro estremamente lungo e complesso, di 340 pagine, pubblicato nel 1963 - W. Feit e J. Tompson mostrarono la validità della congettura, dopo che Brauer nel 1953 e 1954, Suzuki nel 1957 e Thompson nel 1960 avevano compiuto alcuni lavori preliminari. La dimostrazione attinge in modo essenziale a quasi tutto quanto era già noto sui gruppi finiti, compresi i risultati di Phillip Hall sui gruppi risolubili e ai numerosi perfezionamenti apportati da Brauer alla teoria dei caratteri. Vennero inoltre introdotti nuovi metodi di più ampia applicabilità, i quali hanno fortemente influenzato i recenti studi sulla teoria dei gruppi finiti. Questi lavori recenti sono troppo estesi e complicati perché possano essere descritti in questa sede. Basti dire che uno dei temi centrali è stata la classificazione completa di tutti i gruppi semplici finiti soddisfacenti varie condizioni supplementari. In particolare, nel 1968 Thompson determinò i gruppi semplici finiti i cui sottogruppi propri sono tutti risolubili. Per maggiori dettagli rinviamo il lettore al già citato articolo di Feit e ai libri di Feit (1967) e di D. Gorestein (1968), nonché al cap. 3 della voce algebra.
5. Gruppi topologici e gruppi di Lie.
Da un punto di vista moderno, i gruppi continui di Lie avrebbero potuto più appropriatamente chiamarsi gruppi ‛differenziabili'. Da una parte, il calcolo differenziale sostiene un ruolo centrale nella loro teoria; dall'altra, esiste una classe più generale di gruppi che sono ‛continui' senza essere ‛differenziabili'. Questi gruppi più generali, detti gruppi ‛topologici' furono studiati e definiti per la prima volta da O. Schreier nel 1926. Per chiarire questo concetto sarà necessaria una breve digressione nel campo delle nozioni basilari della topologia generale.
Nelle sue ricerche pionieristiche sulla teoria degli insiemi, compiute nel periodo che va dal 1879 al 1884, O. Cantor introdusse la nozione di insiemi ‛aperti' in uno spazio euclideo. Aperto è un insieme A di punti in uno spazio euclideo tale che, per ogni punto p contenuto in A, stanno in A anche i punti q sufficientemente vicini a p. Si dice che A è ‛chiuso' se ogni punto limite dei punti di A sta in A. Si dimostra facilmente che A è aperto se, e soltanto se, è chiuso l'insieme A′ di tutti i p che non appartengono ad A (A′ si chiama l'insieme complementare di A). La conoscenza degli insiemi aperti (o, equivalentemente, la conoscenza di quelli chiusi), fornisce tutti gli elementi essenziali riguardanti continuità e limiti. Basandosi su ricerche antecedenti di M.-R. Fréchet e M. Riesz, F. Hausdorff, nel suo trattato del 1914, Mengenlehre, introdusse la nozione di spazio topologico astratto. Esso non è altro che un insieme S e una famiglia F di sottoinsiemi di S tale che: 1) la parte comune ℴ1 ⋂ ℴ2 di ℴ1 e ℴ2 appartiene a F ogniqualvolta ℴ1 e ℴ2 sono in F; 2) se F1 è una qualsiasi sottofamiglia di F, l'insieme ℴ di tutti i q tali che q ∈ ℴ1 per qualche ℴ1 in F1 è esso stesso un insieme in F; 3) S è in F e l'insieme vuoto è in F.
Gli elementi di F si chiamano sottoinsiemi ‛aperti' dello spazio topologico S e i loro complementari si chiamano sottoinsiemi ‛chiusi'. Una funzione g definita sullo spazio topologico S1 e avente valori nello spazio topologico S2 si dice ‛continua' se g-1(ℴ) è aperto ogniqualvolta ℴ è aperto. In questo caso g-1(ℴ) indica l'insieme di tutti i q in S1 tali che g(q) sia in ℴ. Gli spazi topologici S1 e S2 si chiamano omeomorfi' se esiste una funzione biunivoca g il cui dominio sia S1, il cui rango sia S2, tale che g e g-1 siano entrambe continue. Uno spazio topologico S si chiama ‛spazio di Tychonoff' se ogni insieme costituito da un punto è chiuso; si chiama ‛spazio di Hausdorff' se, dati q1 e q2 con q1 ≠ q2, esistono degli insiemi aperti ℴ1 e ℴ2 che non hanno alcun punto in comune e tali che q1 stia in ℴ1 e q2 in ℴ2 Se S1 e S2 sono spazi topologici, è possibile trasformare l'insieme S1 × S2 di tutte le coppie p, q, con p in S1 e q in S2, in uno spazio topologico, chiamando aperto un sottoinsieme ℴ di S1 × S2 se, e soltanto se, per ogni coppia p, q in ℴ esistono degli insiemi aperti ℴ1 e ℴ2 in S1 e S2, rispettivamente, tali che ℴ1 × ℴ2 contenga p, q e ogni punto di ℴ1 × ℴ2 stia in ℴ.
Un ‛gruppo topologico' è un gruppo G che è anche uno spazio topologico di Tychonoff e in cui la struttura topologica è legata a quella del gruppo in modo che la funzione x, y → xy-1 sia una funzione continua da G × G a G. Un gruppo arbitrario si può trasformare in un gruppo topologico introducendo in esso la topologia in cui ogni sottoinsieme è aperto. Gruppi topologici siffatti si chiamano discreti e lo studio delle loro proprietà è identico a quello dei gruppi astratti. L'esempio più semplice e anche più noto di un gruppo topologico non discreto è il gruppo dei numeri reali con la struttura di gruppo definita dall'addizione. La topologia è la solita: quella cioè in cui A è aperto se, e soltanto se, per ogni x in A esiste un ε positivo tale che, se ∣ y − x ∣ 〈 ε, y sta in A. Un altro importante esempio di gruppo topologico non discreto è GL(n, R), ove R è il corpo dei numeri reali. Per descrivere la topologia di GL(n, R), cominciamo con l'osservare che esso è un sottoinsieme del prodotto di n2 fattori R × R × R ... × R. Ora, ogni sottoinsieme A di uno spazio topologico S diventa esso stesso uno spazio topologico se si prendono come insiemi aperti in A le intersezioni ℴ ⋂ A di A con i sottoinsiemi aperti di S. Data a R × ... × R la topologia prodotto e a GL(n, R) la topologia ‛relativa', GL(n, R) diviene un gruppo topologico, come si vede facilmente. Poiché è facile verificare che un sottogruppo di un gruppo topologico è un gruppo topologico nella topologia relativa, gli esempi di gruppi topologici abbondano e in particolare quelli dei gruppi classici sul corpo dei numeri reali. Naturalmente si possono usare corpi diversi da quelli dei numeri reali purché tali corpi abbiano topologie appropriate. Un corpo è sempre associato a due gruppi commutativi: il gruppo di tutti i suoi elementi composti additivamente e il gruppo di tutti i suoi elementi diversi da zero composti moltiplicativamente. Un corpo topologico è un corpo con una topologia di Tychonoff rispetto alla quale ambedue i gruppi sono topologici. I corpi dei numeri reali e dei numeri complessi sono corpi topologici, come pure i corpi dei numeri p-adici e le loro estensioni. Di essi ci occuperemo in un capitolo successivo. I fatti enunciati più sopra a proposito di GL(n, R) e dei suoi sottogruppi possono applicarsi altrettanto bene a GL(n, E), ove F è un qualsiasi corpo topologico.
In relazione ai gruppi topologici, bisogna distinguere fra sottogruppi chiusi e non chiusi e tra omomorfismi continui e non continui. In generale l'interesse converge soltanto sugli omomorfismi continui e (ma non in modo altrettanto esclusivo) sui sottogruppi chiusi. Se G è un gruppo topologico e H è un suo sottogruppo, lo spazio G/H delle classi laterali destre di H diviene uno spazio topologico quando si prendano come aperti i suoi sottoinsiemi le cui immagini inverse sono aperte in G. Questo spazio topologico è uno spazio di Tychonoff se, e soltanto se, H è chiuso. In tal caso, la funzione s, x ???14??? sx che applica G/H × G su G/H è continua in ambedue le variabili. In particolare, se H è normale, G/H è un gruppo topologico se, e soltanto se, H è chiuso. In tal caso l'omomorfismo di G su G/H è continuo. Due gruppi topologici si dicono isomorfi se, e soltanto se, esiste un isomorfismo fra essi, considerati come gruppi astratti, il quale sia anche un omeomorfismo.
Uno spazio topologico si dice ‛connesso' se nessuno dei suoi sottoinsiemi propri (e distinti dall'insieme vuoto) è simultaneamente aperto e chiuso. Ogni punto è contenuto in un insieme che è il più grande fra gli insiemi contenenti quel punto che sono connessi per la topologia relativa. Esso si chiama ‛componente connessa' del punto considerato. Uno spazio le cui componenti connesse constino tutte di un solo punto si chiama ‛totalmente sconnesso'. Uno spazio topologico può essere totalmente sconnesso senza essere discreto; ne è un esempio il corpo topologico dei numeri p-adici. Se G è un gruppo topologico, la componente connessa dell'identità è sempre un sottogruppo normale chiuso il cui gruppo quoziente è totalmente sconnesso. In particolare, un gruppo topologico semplice è connesso oppure è totalmente sconnesso. I gruppi semplici definiti dai gruppi classici su corpi topologici sono sconnessi se, e soltanto se, i corpi stessi sono sconnessi. I corpi dei numeri reali e complessi sono esempi di corpi topologici connessi.
Uno spazio topologico S si dice ‛compatto' se ogni famiglia F di insiemi aperti che copre S (nel senso che ogni p in S sta in qualche ℴ in F) contiene qualche sottofamiglia finita che copre S. Si dice che lo spazio S è ‛localmente compatto' se ogni punto di S è contenuto in un insieme la cui ‛chiusura' e compatta. (La chiusura di un insieme è il più piccolo insieme chiuso che lo contiene). I sistemi di numeri reali e complessi sono localmente compatti, ma non compatti; i loro sottoinsiemi compatti sono esattamente quei sottoinsiemi che sono al tempo stesso chiusi e limitati. Quando F è un corpo topologico localmente compatto, GL(n, F) e tutti i suoi sottogruppi chiusi sono gruppi topologici localmente compatti. Oltre ai corpi dei numeri reali e dei numeri complessi, i corpi dei numeri p-adici e le loro estensioni finite sono localmente compatte. È chiaro che i gruppi discreti sono localmente compatti e sono compatti se, e soltanto se, sono finiti. L'esempio più semplice di un gruppo compatto non finito è il quoziente del gruppo additivo della retta reale per il sottogruppo di tutti i multipli interi di un numero reale assegnato λ diverso da zero. A meno di un isomorfismo, questo quoziente non dipende dalla scelta di λ, e si chiama toro a una dimensione. Il suo prodotto diretto con se stesso k volte è il toro a k dimensioni. In generale, il prodotto diretto di due gruppi localmente compatti è localmente compatto e il prodotto diretto di due gruppi compatti è compatto. Inoltre, sottogruppi chiusi e quozienti di gruppi compatti (rispettivamente localmente compatti) sono anch'essi gruppi compatti (rispettivamente localmente compatti). Se Fè il corpo dei numeri complessi e z → ÿ è l'automorfismo che porta ciascun numero complesso nel suo coniugato, il sottogruppo unitario corrispondente di GL(n, F) è un gruppo compatto, che è isomorfo al toro a una dimensione quando n è uno, ma non è commutativo negli altri casi. Gli altri gruppi classici compatti sono sottogruppi chiusi di questi.
Si dice che il gruppo topologico G è ‛localmente euclideo', se esiste un insieme aperto ℴ contenente l'identità e, tale che ℴ è isomorfo al prodotto diretto di un numero finito di copie del corpo dei numeri reali, o, equivalentemente, al sottoinsieme ditale prodotto costituito da tutti gli x1, ..., xn con x²1 + x²2 + ... + x²n 〈 1. Dato un ℴ siffatto nel gruppo localmente euclideo G, si scelga ℴ′ in modo che xy-1 appartenga a ℴ per tutti gli x e y in ℴ′. Poiché x, y e xy-1 possono essere rappresentati dalle n-uple di numeri reali, l'applicazione x, y → xy-1 di ℴ′ × ℴ′ in ℴ si può descrivere mediante n funzioni di 2n variabili reali, la k-esima delle quali fornisce la k-esima componente della n-upla che rappresenta xy-1 in funzione delle 2n componenti delle n-uple associate a x e y. Se queste ‛coordinate' possono essere introdotte in modo che le n funzioni delle 2n variabili siano analitiche invece che soltanto continue, si dice che il gruppo topologico è un ‛gruppo di Lie'. A conclusione di una lunga serie di ricerche che nel 1952 culminò nella pubblicazione simultanea di due lavori complementari di D. Montgomery e L. Zippin da una parte e di A. M. Gleason dall'altra, è ora acquisito il fatto che ogni gruppo localmente euclideo è di fatto un gruppo di Lie.
Come mostrò lo stesso Lie, ai gruppi di Lie possono applicarsi strumenti analitici particolarmente profondi e completi, legati ai metodi del calcolo differenziale. A ogni gruppo di Lie si associa un'algebra non associativa di dimensione finita che si chiama ‛algebra di Lie' del gruppo, la quale può considerarsi come una ‛versione infinitesimale' del gruppo. Sebbene sia uno strumento molto più complicato e sofisticato della derivata di una funzione in un punto, in un certo senso l'algebra di Lie di un gruppo può essere identificata con la ‛derivata del gruppo nell'identità'.
Le algebre di Lie possono essere studiate e classificate con i metodi dell'algebra lineare e i risultati sono estremamente importanti proprio in relazione ai gruppi di Lie, in quanto la corrispondenza fra gruppi di Lie e algebre di Lie non è molto lontana dalla biunivocità. In particolare, due gruppi di Lie G1 e G2 hanno algebre di Lie isomorfe se, e soltanto se, essi sono ‛localmente isomorfi', nel senso che esistono due insiemi aperti ℴ1 e ℴ2, rispettivamente in G1 e G2, e un omeomorfismo ϕ di ℴ1 su ℴ2 tale che, se x e y stanno in ℴ1, xy e x-1 stanno in ℴ1 se, e soltanto se, ϕ(x)ϕ(y) e ϕ(x)-1 stanno in ℴ2, avendosi allora ϕ(xy) = ϕ(x)ϕ(y) e ϕ(x-1) = ϕ(x)-1. Inoltre, fra tutti i gruppi di Lie aventi un'algebra di Lie assegnata, ne esiste uno e uno solo (definito a meno di un isomorfismo) il quale è semplicemente connesso. Nel caso che Γ sia un sottogruppo chiuso numerabile del centro di questo gruppo di Lie G semplicemente connesso, il gruppo quoziente GΓ è un gruppo di Lie connesso localmente isomorfo a G e ogni gruppo di Lie connesso localmente isomorfo a G è isomorfo a G/Γ, Γ essendo un sottogruppo chiuso numerabile del centro di G.
Vedremo presto come sia conveniente definire l'algebra di Lie del gruppo di Lie G mediante i cosiddetti ‛sottogruppi a un parametro', cioè mediante gli omomorfismi continui t → ϕ(t) del gruppo additivo della retta reale in G. Diremo che una funzione a valori reali f su G è ‛differenziabile' se esistono un insieme aperto ℴ, contenente l'identità, e un sistema di coordinate analitiche in ℴ, tali che, per ogni x in G, la funzione y → f(yx-1) sia, al variare di y in ℴ, differenziabile infinite volte nel senso abituale rispetto alle coordinate definite in ℴ.
Indicheremo con C∞ (G) l'insieme di tutte le funzioni indefinitamente differenziabili. Per ogni f in C∞(G) esiste
qualunque sia x, e fϕ è ancora in C∞(G). Tale limite può considerarsi come un tipo di derivata parziale generalizzata.
Non è difficile mostrare che per ogni coppia di sottogruppi a un parametro, ϕ1 e ϕ2, ne esiste un terzo, ϕ3 tale che = fϕ2+fϕ2 per tutte le f in C∞(G). Chiamiamo ϕ3 la somma di ϕ1 e ϕ2 e scriviamo ϕ3 = ϕ1 + ϕ2. Si dimostra che l'insieme LG di tutti i sottogruppi a un parametro è un gruppo commutativo rispetto all'operazione di addizione ora definita. Se λ è un numero reale qualsiasi e ϕ è un elemento di LG, t → ϕ(λt) è chiaramente un elemento di LG, che indicheremo con λϕ. Si vede facilmente che fλϕ = λfϕ e che, rispetto a questa operazione, LG è uno ‛spazio vettoriale di dimensione finita sui numeri reali'. In generale, se V è un gruppo commutativo e λϕ è definito e appartiene a V per tutti i ϕ in V e per tutti i λ in un corpo F, si dice che V è uno spazio vettoriale su F quando ϕ → λϕ è un endomorfismo α di V e λ → αλ è un omomorfismo di F sull'anello di tutti gli endomorlismi di V che porta l'identità nell'identità. Si dice che questo spazio vettoriale ha dimensione finita n se esiste una ‛base' di n elementi, cioè se esiste in esso un insieme di n elementi ϕ1, ϕ2, ϕn tali che ogni elemento abbia una e una sola rappresentazione λ1ϕ1 + ... + λnϕn, ove i λj appartengono a F. Dati ϕ1 e ϕ2 in LG, si può dimostrare che esiste un unico ϕ3 in L tale che fϕ3 = fϕ1ϕ2 − fϕ2ϕ1 per tutte le f in C∞ (G). Indicando ϕ3 con [ϕ1ϕ2], l'operazione ϕ1, ϕ2 ???14??? [ϕ1, ϕ2] è ‛lineare' in ciascuna variabile, nel senso che commuta con l'addizione ([ϕ1, ϕ2 + ϕ3] = [ϕ1, ϕ2] + [ϕ2, ϕ3]) e con la moltiplicazione per numeri reali ([ϕ1, λϕ2] = λ[ϕ1, ϕ2]). Tuttavia non vale la legge associativa usuale della moltiplicazione, ma al suo posto si ha la cosiddetta identità di Jacobi: [[ϕ1, ϕ2], ϕ3] + [[ϕ3ϕ1], ϕ2] + [[ϕ2ϕ3], ϕ1] = 0. Ovviamente la nostra ‛moltiplicazione' non associativa ϕ1ϕ2 ???14??? [ϕ1, ϕ2] è ‛antisimmetrica', nel senso che [ϕ1, ϕ2] 0 − [ϕ2, ϕ1] per tutte le ϕ1 e ϕ2. In generale, dato uno spazio vettoriale arbitrario L su un corpo F nel quale sia definita una ‛moltiplicazione' bilineare antisimmetrica ϕ1, ϕ2 → [ϕ1, ϕ2] che soddisfi l'identità di Jacobi, L si chiama un'‛algebra di Lie' su F. L'algebra di Lie reale LG sopra definita si chiama ‛algebra di Lie del gruppo di Lie G'.
6. La struttura delle algebre di Lie e dei gruppi di Lie connessi.
Come abbiamo indicato nell'ultimo capitolo, si può in notevole misura ridurre lo studio dei gruppi di Lie connessi allo studio delle loro algebre di Lie. Corrispondentemente, si può prevedere di ottenere una teoria della struttura delle algebre di Lie parallela alla teoria della struttura dei gruppi finiti e dei gruppi più generali descritti nei capitoli precedenti. L'analogo di un sottogruppo nelle algebre di Lie è una sottoalgebra, cioè un insieme che contiene ϕ1 + ϕ2, [ϕ1, ϕ2] e λϕ1 ogniqualvolta contiene ϕ1 e ϕ2, per ogniλ nel corpo F. Un'applicazione h da un'algebra di Lie L1 a un'algebra di Lie L2 si chiama un ‛omomorfismo' se h(λ1ϕ1 + λ2ϕ2) = λ1h(ϕ1) + λ2h(ϕ2) e h([ϕ1, ϕ2]) = [h(ϕ1), h(ϕ2)) per tutti i ϕ1 e ϕ2 contenuti in L1 e per tutti i λ appartenenti al corpo F. Se h è biunivoca, e se la sua immagine è tutta L2, essa si dice un ‛isomorfismo'; se esiste in isomorfismo tra L1 e L2, queste ultime si dicono ‛isomorfe'. L'insieme di tutti i ϕ tali che h(ϕ) = 0 si chiama il ‛nucleo', Kh, dell'omomorfismo h. Esso è sempre una sottoalgebra con la proprietà aggiuntiva che [ϕ, ψ] è in Kh per tutti i ϕ in Kh e tutti i ψ in L1. Le sottoalgebre dotate di questa proprietà si chiamano ‛ideali'. Gli ideali sono l'analogo, nell'ambito delle algebre di Lie, dei ottogruppi normali. Se I è un ideale nell'algebra di Lie L, possiamo introdurre una relazione di equivalenza ~ dicendo che ϕ1 ~ ϕ2 ogniqualvolta ϕ1 − ϕ2 ∈ I. Sia g(ϕ) la classe di equivalenza di ϕ e sia L/I l'insieme di tutte le classi di equivalenza. Si vede facilmente che g([ϕ1, ϕ2]) e g(λ1ϕ1 + λ2ϕ2) dipendono soltanto da g(ϕ1) e g(ϕ2) e che L/I diventa un'algebra di Lie qualora si ponga [g(ϕ1), g(ϕ2)] = g([ϕ1, ϕ2]) e λ1g(ϕ1) + λ2g(ϕ2) = g(λ1 + λ2ϕ2) per tutti i ϕ1 e ϕ2 in L e tutti i λ1 e λ2 nel corpo F. L'algebra di Lie definita in questo modo si chiama il ‛quoziente' di L per I. Essa è l'oggetto analogo, nell'ambito delle algebre di Lie, del quoziente G/N di un gruppo G per un suo sottogruppo normale. L'applicazione g è un omomorfismo di L su L/I il cui nucleo è I e ogni omomorfismo h di L1 in L2 definisce un isomorfismo di L1/Kh con la sottoalgebra di L2 che è l'immagine di h. Un'algebra di Lie priva di ideali non banali, vale a dire priva di ideali diversi da zero e da tutta se stessa, si chiama ‛semplice'. Come per i gruppi, il problema di trovare tutte le algebre di Lie a meno di isomorfismi può ridursi a trovare le algebre di Lie semplici e a un problema di estensione.
L'algebra di Lie L si dice ‛risolubile' se esiste una famiglia L = I0 ⊃ I1 ⊃ I2 ⊃ ... ⊃ In = 0 di sottoalgebre tali che Ij sia un ideale in Ij-1 e Ij/Ij+1 sia commutativo nel senso che [ϕ, ψ] = 0 per tutti i ϕ e i ψ in Ij/Ij+1. Si vede facilmente che un gruppo di Lie connesso è commutativo se, e soltanto se, la sua algebra di Lie è commutativa in questo senso. Se L è una qualsiasi algebra di Lie, allora L1, l'insieme di tutte le somme di ‛commutatori' [ϕ, ψ], è un ideale, come si vede facilmente, e si ottiene una successione di ideali ???41???1, ???41???2, ... in modo induttivo: ???41???n è l'insieme di tutte le somme di commutatori [ϕ, ψ], ove ϕ è in ???41???n-1 e ψ è in L. Se ???41???n = 0 per qualche n, si dice che L è ‛nilpotente'. Un'algebra di Lie nilpotente è sempre risolubile, ma non è vero l'inverso. Un teorema molto importante afferma che ogni algebra di Lie a dimensione finita ha un ideale risolubile R il quale è massimale nel senso che esso contiene ogni altro ideale massimale risolubile. Questo unico ideale massimale risolubile si chiama il ‛radicale' dell'algebra di Lie L. Ovviamente l'algebra di Lie quoziente L/R ha radicale 0.
Date le algebre di Lie L1, L2, ..., Ln, la loro somma diretta L1 + L2 + ... + Ln è la somma di tutte le ϕ1, ϕ2, ..., ϕn con ϕj ∈ Lj, con la struttura di algebra di Lie definita nel modo seguente:
[ϕ1, ϕ2, ..., ϕn, ψ1, ψ2, ..., ψn] =
[ϕ1, ψ1], [ϕ2, ψ2], ..., [ϕn, ψn]
λ(ϕ1, ϕ2, ..., ϕn) + μ(ψ1, ψ2, ..., ψn) =
= λϕ1 + μψ1, λϕ2 + μψ2 + ... λϕn + μψn.
Se il corpo F ha ‛caratteristica zero', nel senso che 1 + 1 + ... non è mai zero, un'algebra di Lie di dimensione finita con radicale zero è isomorfa a una somma diretta di algebre di Lie semplici, non commutative, finite. Inversamente, ogni somma diretta siffatta ha radicale zero. Algebre di Lie isomorfe a somme dirette di algebre semplici non commutative si dicono ‛semisemplici'. Dunque, quando F ha caratteristica zero, ogni algebra di Lie di dimensione finita ha un ideale risolubile il cui quoziente è una somma diretta di algebre semplici non commutative. Non esiste per i gruppi finiti un risultato analogo a questo. Non sempre è possibile trovare una serie di composizione con tutti i fattori commutativi in fondo. Inoltre, anche quando non vi sono fattori commutativi, il gruppo non è necessariamente un prodotto di gruppi semplici.
Un altro risultato incisivo, in contrasto con la teoria dei gruppi finiti, è che le algebre di Lie semplici di dimensione finita sui numeri reali e complessi sono state completamente classificate. Mentre sono soltanto le algebre di Lie sui reali che intervengono direttamente nella classificazione dei gruppi di Lie, sono le algebre di Lie complesse quelle che hanno un'importanza rilevante come strumento per classificare le algebre di Lie reali. Sia L un'algebra di Lie arbitraria sul corpo dei numeri reali. Per complessificazione LC di L s'intende l'algebra di Lie complessa i cui elementi sono le coppie ordinate ϕ1, ϕ2 di elementi di L e ove le operazioni sono definite nel modo seguente:
λ(ϕ1, ϕ2) + μ(ψ1, ψ2) = λϕ1 + μψ1, λϕ2 + μϕ2
i(ϕ1, ϕ2) = − ϕ2, ϕ1
[(ϕ1, ϕ2), (ψ1, ψ2)] = [ϕ1, ψ1] − [ϕ2, ψ2], [z2, ψ1] + [ϕ1, ψ2]
per tutti i numeri reali λ e μ e tutti i ϕ1, ϕ2, ψ1, ψ2 in L. La complessificazione di un'algebra di Lie reale semplice è sempre un'algebra di Lie semplice complessa o la somma diretta di due algebre di Lie semplici complesse isomorfe. Inoltre quest'ultimo caso si presenta soltanto quando l'algebra di Lie reale si ottiene da un'algebra di Lie complessa ignorando la moltiplicazione per scalari non reali. Pertanto esiste un'applicazione naturale univoca ma non biunivoca delle classi d'isomorfismo delle algebre di Lie semplici reali in classi d'isomorfismo di algebre di Lie semplici complesse, e questa applicazione risulta essere surgettiva. Poiché le algebre di Lie semplici complesse sono le più semplici da trattare, si classificano prima queste e quindi le possibili ‛forme reali' di ciascuna algebra di Lie semplice complessa. Ogni algebra semplice complessa ha un'unica forma reale che è l'algebra di Lie di un gruppo compatto di Lie. Dunque, classificando le algebre di Lie semplici complesse si classificano direttamente i gruppi di Lie semplici compatti connessi. Allo stesso modo si classificano anche i gruppi di Lie semplici connessi che sono anche complessi nel senso che le complessificazioni delle loro algebre di Lie sono somme dirette di due algebre di Lie semplici isomorfe.
La classificazione completa delle algebre di Lie complesse semplici di dimensione finita fu portata a termine da E. Cartan nella sua tesi del 1894 basata su un precedente studio incompleto di W. Killing.
Consideriamo i gruppi classici sopra il corpo complesso come li abbiamo descritti nel cap. 4. Essi includono SL(m, C), SO(n, C) e Sp(n, C), ove SO(n, C) è il gruppo speciale ortogonale. Per il corpo complesso esiste soltanto un gruppo ortogonale per ogni n, a meno di isomorfismi. Questi gruppi sono tutti i gruppi di Lie complessi le cui algebre di Lie ammettono una moltiplicazione per i che le trasforma in algebre di Lie complesse. Queste algebre di Lie complesse vengono abitualmente indicate con i simboli An-1, Bn-1/2 o Dn/2, a seconda che n sia pari o dispari, e con Cn cosicché Am, Bm, Dm sono definite per m = 1, 2, 3,... e sono tutte semplici e non commutative, eccettuate D1 e D2. A1, B1 e C1 sono fra loro isomorfe; B2 è isomorfa a C2 e A3 è isomorfa a D3. Non esistono tuttavia altri isomorfismi, così che A1, A2, A3,..., B2, B3, ..., C3, C4, ..., e D4, D5,... sono algebre di Lie semplici complesse non commutative a due a due non isomorfe. Cartan dimostrò che, a meno di cinque casi eccezionali, ogni classe d'isomorfismo di un'algebra semplice complessa di Lie di dimensione finita contiene un elemento di una di queste quattro successioni infinite. Le cinque algebre eccezionali vengono indicate con i simboli G2, F4, E6, E7 ed E8 e hanno rispettivamente dimensioni 14, 52, 78, 133 e 248. Non tentiamo neppure di descriverle in maggior dettaglio in questa sede. Naturalmente le algebre di Lie Am, Bm, Cm e Dm possono venir descritte direttamente invece che come algebre di Lie di certi gruppi. Per esempio, Am è isomorfa allo spazio vettoriale delle matrici complesse di tipo (m + 1) × (m + + 1) di traccia zero e [u, v] è definito da uv − vu.
Il problema di trovare tutte le forme reali di un'algebra di Lie semplice complessa fu risolto da É. Cartan nel 1914. Sia L un'algebra complessa e sia σ un automorfismo di L come algebra di Lie ‛reale', tale che σ2 sia l'identità e σ(iu) = −iσ(u) per tutti gli u. Sia Lσ l'insieme di tutti i ϕ in L con σ(ϕ) = ϕ. Lα è un'algebra di Lie reale la cui complessificazione è L e ogni forma reale di L può essere ottenuta con un'opportuna scelta di σ. Cartan trovò tutti i possibili σ per ogni algebra di Lie semplice complessa di dimensione finita e quindi tutte le algebre di Lie semplici reali di dimensione finita. In ognuno dei casi indicati vi è soltanto un numero finito di forme reali non isomorfe.
Per il gruppo SL(n, C) si vede facilmente che ogni elemento può essere scritto in modo unico nella forma nak, ove n è un elemento del sottogruppo nilpotente N di tutte le matrici che sono zero sopra la diagonale e uno sulla diagonale, a è un elemento del gruppo commutativo A di tutte le matrici diagonali con determinante uno ed elementi positivi e k è un elemento del sottogruppo compatto K di tutte le matrici unitarie con determinante uno.
Questo risultato elementare è un caso speciale di un teorema che vale per una larga classe di gruppi di Lie semisemplici. (Un gruppo di Lie si dice semisemplice se è connesso e ha un'algebra di Lie semisemplice). Sia G un gruppo di Lie semisemplice compatto connesso con un centro finito, la cui algebra di Lie non abbia componenti semplici che siano algebre di Lie di gruppi di Lie compatti. In tale ipotesi G contiene sottogruppi connessi chiusi N, A e K tali che N è nilpotente, A è isomorfo al prodotto diretto di un numero finito di repliche del gruppo additivo della retta reale e K è compatto. Inoltre, n, a, k → nak è un'applicazione biunivoca e bicontinua da N × A × K in G e K non è contenuto propriamente in nessun sottogruppo compatto di G. Questo importante teorema, dimostrato da Iwasawa nel 1949, è noto come teorema di struttura di Iwasawa.
7. Rappresentazioni, caratteri e dualità gruppi finiti.
Sia G un gruppo finito. Una ‛rappresentazione' di G su di un corpo ℱ è un omomorfismo x → Vx di G nel gruppo di tutte le trasformazioni lineari invertibili di uno spazio vettoriale ℋ(V) su ℱ. Quando ℋ(V) ha dimensione finita e ha una base ϕ1, ϕ2, ... ϕn, allora Vx(ϕi) = Σ vij(x)ϕj e x → ∥ vij(x) ∥ è un omomorfismo di G nel gruppo di tutte le matrici n × n su ℱ. Da un punto di vista teorico è preferibile utilizzare trasformazioni lineari Vx piuttosto che loro realizzazioni concrete mediante matrici. Le due rappresentazioni V1 e V2 si dicono ‛equivalenti' (V1≃V2) se esiste una trasformazione lineare invertibile T di ℋ(V1) su ℋ(V2) tale che, per tutte le x ∈ G, V²x = TV¹xT-1. Di solito non si distingue fra rappresentazioni equivalenti e uno dei problemi più importanti consiste nel determinare tutte le possibili classi di equivalenza per un dato G e un dato ℱ. Se V1 e V2 sono due rappresentazioni (sullo stesso corpo ℱ), definiamo la loro somma diretta V1 ⊕ V2 come la rappresentazione il cui spazio ℱ(V1 ⊕ V2) è lo spazio vettoriale di tutte le coppie ϕ1, ϕ2 con ϕ1 in ℋ(V1) e ϕ2 in ℋ(V2) e dove, per ogni x in G, (V1 + V2)x(ϕ1, ϕ2) = V¹x(ϕ1), V²x(ϕ2). Una rappresentazione che non sia equivalente alla somma diretta di altre due rappresentazioni si dice ‛indecomponibile'. Segue facilmente dalle definizioni che (V1 ⊕ V2) ⊕ V3 ≃ V1 ⊕ (V2 ⊕ V8), cosicché si può scrivere senza ambiguità V1 ⊕ V2 ⊕ V3 e, più in generale, V1 ⊕ V2 ⊕ ... ⊕ Vn. Ovviamente, ogni rappresentazione di dimensione finita V è equivalente a una rappresentazione V1 ⊕ V2 ⊕ ... ⊕ Vn, ove tutte le Vj sono indecomponibili, e non è difficile dimostrare che n e le componenti indecomponibili Vj sono determinate univocamente a meno di equivalenze. Il problema di determinare tutte le classi di equivalenza delle rappresentazioni di dimensione finita si riduce quindi al problema corrispondente per le rappresentazioni indecomponibili. Un sottospazio ℋ1 di ℋ1(V) si dice ‛invariante' se Vx(ϕ) è in ℋ1 per tutti i ϕ in ℋ1 e tutti gli x in G. Dato un tale sottospazio, si ottiene una nuova rappresentazione Vℋ1 il cui spazio è ℋ1 prendendo come Vxℋ1 l'operatore che si ottiene restringendo Vx a ℋ1. Vℋ1 si chiama una ‛sottorappresentazione' di V. Se non esiste nessun ℋ1 invariante (eccetto 0 e ℋ(V)), si dice che V è ‛irriducibile'. Due sottospazi invarianti ℋ1 e ℋ2 si dicono 'complementari' se ℋ1 ⋂ ℋ2 = {0} e ℋ1 e ℋ2 generano ℋ(V). In questo caso si può constatare facilmente che V ≃ Vℋ1 ⊕ Vℋ2.
Nella teoria classica, come in molte applicazioni, ℱ è il corpo dei numeri complessi. Ci atterremo tacitamente a questo assunto finché non faremo esplicitamente un'ipotesi diversa. Un'importante conseguenza è che, ogniqualvolta ℋ(V) ha dimensione finita, esiste in esso un prodotto interno invariante definito positivo; esiste cioè una funzione ϕ, ϕ → (ϕ • ψ) che trasforma coppie di elementi in numeri complessi in modo che (ϕ • ϕ) > 0 per ϕ ≠ 0, (ϕ • ψ) = (-ψ- •- -ϕ), (λϕ + μϑ) • ψ = λ(ϕ •ψ) + μ(ϑ • ψ) e (Vx(ϕ) • Vx(ψ)) = (ϕ • ψ) = 0 per tutti i numeri complessi λ, μ, tutti i ϕ, ψ e ϑ in ℋ(V) e tutti gli x in G. L'insieme di tutte le ϕ in ℋ(V) tale che (ϕ • ψ) = 0 per tutte le ψ in ℋ1 si chiama il ‛complemento ortogonale' ℋ1⊥ di ℋ1 e si vede facilmente che ℋ1⊥ è un sottospazio complementare invariante ogniqualvolta ℋ1 è invariante. Ogni rappresentazione indecomponibile di dimensione finita è irriducibile e basta quindi determinare le classi di equivalenza di una rappresentazione irriducibile per determinare tutte le altre. Questo è importante in quanto per ogni G finito esiste soltanto un numero finito di classi di equivalenza di rappresentazioni irriducibili di G.
Si definisce la ‛traccia' di una matrice finita n × n ∥ Gij ∥ come la somma diagonale G11 + G22 + ... + Gnn e si verifica immediatamente che Traccia (AB) = Traccia (BA), cosicché Traccia (ABA-1) = Traccia B ogniqualvolta A è invertibile. Ne segue che la traccia di una matrice di una trasformazione lineare rispetto a una base è la stessa per tutte le basi, cosicché si può parlare senza tema di ambiguità di Traccia (A) di una trasformazione lineare A. Per ogni rappresentazione di dimensione finita V del gruppo finito C si definisce una funzione a valori complessi χV su G, ponendo χV(x) = Traccia V. Poiché Traccia (ABA-1) = Traccia B, ne segue che la funzione χV dipende soltanto dalla classe di equivalenza di V. Inversamente si può dimostrare che V1 e V2 sono equivalenti ogniqualvolta sia χV1(x) = χV2(x) per tutti gli x. La funzione χV si chiama il ‛carattere' della rappresentazione V. È chiaro che χV1+V2 (x) ≡ χV(x) + χV2(x), cosicché ogni carattere è una somma finita di caratteri irriducibili (cioè di caratteri di rappresentazioni irriducibili). Siano χV e χW due caratteri irriducibili. Si può dimostrare che (indicando con o(G) l'ordine di G)
oppure è uguale a zero a seconda che V e W siano equivalenti oppure no. Ne segue in particolare che caratteri irriducibili distinti χV1, ..., χVj sono linearmente indipendenti nel senso che ΣλjχVj(x) ≡ 0 implica λj = 0 per tutti i j. Poiché χV(yxy-1) = Traccia (VyVxVy-1) = Traccia (Vx) = χV(x), ogni carattere è una ‛funzione di classe', cioè è costante su ogni classe coniugata. Poiché, per la teoria generale della dipendenza lineare, non possono esservi più di k funzioni linearmente indipendenti definite su un insieme di k elementi, possiamo concludere che vi sono al più tanti caratteri distinti irriducibili quante sono le classi coniugate distinte in G. Di fatto ci sono tanti caratteri irriducibili quante sono le classi, cosicché ogni funzione di classe può essere espressa in modo unico nella forma λ1χV1 + ... + λjχVk, ove i χV1, ..., χVk sono caratteri irriducibili distinti e i λj sono numeri complessi. I caratteri naturalmente sono quelle funzioni di classe per le quali i λj sono interi non negativi.
Denotiamo con ℋ(V) lo spazio vettoriale di tutte le funzioni complesse su G e definiamo (Vzf)(y) = f(yx) per tutti gli x, y in G e tutte le f in ℋ(V). Si verifica immediatamente che V è una rappresentazione; essa è chiamata la rappresentazione regolare. Un calcolo ovvio mostra che il suo carattere χV è zero ovunque eccetto che sull'identità e, dove assume il valore o(G). Scrivendo χV = n1χ1 + ... + nkχk, ove i χi sono caratteri irriducibili distinti, e calcolando ΣχV(x)-χj(x) a partire dalle relazioni di ortogonalità citate dianzi e da χV, si ottiene che o(G) χj(e) = o(G)nj, cosicché nj = χj(e). In altre parole χV(x) ≡ Σjχj‛(e)χj, cosicché la rappresentazione regolare contiene ‛ogni' rappresentazione irriducibile come una sottorappresentazione e la contiene con molteplicità uguale alla dimensione dello spazio in cui questa opera. Posto x = e nell'equazione precedente, si deduce che o(G) = Σj[χj(e)]2, cosicché la somma dei quadrati delle dimensioni di tutte le rappresentazioni irriducibili distinte è uguale all'ordine del gruppo.
Se ℋ(V) ha dimensione 1, è Vx = f(x)I, ove I è l'operatore identità e f è una funzione da G ai numeri complessi non nulli tale che f(xy) = f(x)f(y) per tutti gli x e y in G; in altre parole, f è un omomorfismo di G nel gruppo moltiplicativo di tutti i numeri complessi non nulli. Di fatto, poiché xk = e per qualche k, f(xk) = (f(x))k = 1 e ∣ f(x) ∣ = 1, in quanto f(x) è la radice k-esima dell'unità. Inversamente, dato un qualsiasi omomorfismo f da G ai numeri complessi di valore assoluto uno, l'applicazione x ???14??? f (x)I è una rappresentazione di G di dimensione 1, e quindi irriducibile, il cui carattere è f In altre parole, i caratteri delle rappresentazioni di dimensione 1 di G non sono altro che omomorfismi di G sul gruppo di tutti i numeri complessi di valore assoluto 1'. Ci si riferisce talvolta a essi come ai ‛caratteri di dimensione 1'. Quando G è commutativo, segue facilmente dal teorema fondamentale dell'algebra che ogni rappresentazione irriducibile di G ha dimensione 1. Poiché in questo caso le classi coniugate sono tutte insiemi costituiti da un solo elemento, ci devono essere esattamente tanti caratteri di dimensione 1, tra loro distinti, quanti sono gli elementi del gruppo e ogni funzione a valori complessi g su G deve essere esprimibile in modo univoco nella forma g(x) Σnj=1 λjχj(x), ove i λj sono numeri complessi e i χj sono gli omomorfismi distinti di G nei numeri complessi di valore assoluto 1.
Si osservi che il prodotto di due qualsiasi caratteri a una dimensione è ancora un carattere a una dimensione e, rispetto a questo prodotto, l'insieme di tutti i caratteri a una dimensione è un gruppo Ø che si chiama ‛guppo dei caratteri' o ‛gruppo duale' del gruppo finito commutativo G. Per ogni x in G, sia f2(χ) = χ(x) per tutti i χ ∈ Ø.fx è un carattere del gruppo G ed è chiaro che fxy = fxfy per tutti gli x e y in G. Pertanto χ → fx è un omomorfismo di G in Ø che, come si venfica subito, è un isomorfismo surgettivo. Si ha così un'‛identificazione' naturale di G con Ø che rende la relazione tra G e Ø completamente reciproca e giustifica l'uso del termine duale. Se G1 e G2 sono gruppi commutativi finiti e ϑ è un isomorfismo di G1 in G2, esiste ‛uno e un solo omomorfismo duale' ϑ* di Ø2 in Ø1 caratterizzato dall'identità χ(ϑ(x)) = ϑ*(χ)(x). Identificando G con Ø si riconosce che ϑ** = ϑ. Nel caso speciale in cui G1 sia un sottogruppo di G2 e ϑ sia l'omomorfismo di immersione, si verifica che ϑ* è un omomorfismo di Ø2 in Æ1 il cui nucleo è il cosiddetto annullatore G1⊥ di G1 in Ø1; cioè è il sottogruppo di tutti i χ tali che χ(x) = 1 per tutti gli x in G1. L'applicazione H ???14??? H⊥ è un'applicazione biunivoca, che inverte l'inclusione, dei sottogruppi di G nei sottogruppi di Ø, tale che H⊥⊥ = H.
Il teorema di sviluppo secondo cui f (x) = Σχ∈-G λχ(x) partecipa anch'esso alla dualità. Di fatto, i coefficienti λχ si possono considerare come valori di una funzione χ ???14??? λ(x) definita su Ø e dalle relazioni di ortogonalità discende la formula:
Posto per definizione
si riconosce che
cosicché le funzioni su G e i coefficienti dei loro sviluppi, considerati come funzioni su Ø, sono legati gli uni agli altri in modo reciproco. È interessante confrontare queste formule con le formule di inversione che si incontrano nella teoria delle trasformate di Fourier in analisi:
tenendo conto del fatto che z ???14??? eiyx è, per ogni y, un omomorfismo continuo del gruppo additivo dei numeri reali nel gruppo dei numeri complessi di valore assoluto 1. Come vedremo in seguito, ambedue questi insiemi di formule sono casi speciali della teoria delle ‛trasformazioni di Fourier generalizzate' applicabili a gruppi commutativi localmente compatti arbitrari.
Il problema di trovare tutti i caratteri di dimensione i (e quindi tutte le rappresentazioni irriducibili) di un gruppo commutativo finito si risolve facilmente. Quando G è ciclico con generatore a, si ha χ(ak) = χ(a)k e χ(e) = 1. Se G è di ordine n, χ(a) dev'essere una radice n-esima dell'unità, exp(2πil/n), dove l = 0, i, 2,..., n − 1 e per ogni l esiste un unico carattere χ con χ(ak) = exp(2nilk/n) per k = 0, i, 2,..., n − 1. Quando G non è ciclico, G è isomorfo a G1 × G2 × ... × Gn, ove i Gj sono tutti ciclici; si ha allora il seguente risultato di carattere generale. Sia G = G1 × G2, ove G1 e G2 sono gruppi finiti (non necessariamente commutativi). Siano χ1 e χ2 caratteri irriducibili rispettivamente di G1 e G2. Posto (χ1 × χ2)(x, y) = χ1(x)χ2(y), χ1 × χ2 è un carattere irriducibile di G1 × G2 e ogni carattere irriducibile si può ottenere in questo modo. χ1 × χ2 ha dimensione 1 se, e soltanto se, χ1 e χ2 hanno ambedue dimensione 1 e in questo caso speciale il teorema è del tutto banale. Ne segue che esiste un isomorfismo naturale di G1 × G2 × ... × Gn con Ø1 × Ø2 × ... × Øn e che conoscere Ø per i gruppi ciclici commutativi equivale a conoscerlo per tutti i gruppi commutativi finiti.
I gruppi finiti non commutativi hanno sempre caratteri irriducibili di dimensione diversa da 1 e trovare questi ultimi può rivelarsi un problema niente affatto banale. Come nel caso commutativo, si studia prima di tutto la relazione tra le rappresentazioni irriducibili di un gruppo e quelle dei suoi sottogruppi; è necessario tuttavia considerare in questo caso sottogruppi molto più generali dei fattori di una decomposizione in prodotto diretto. Uno strumento essenziale è la nozione di ‛carattere indotto', introdotta da Frobenius proprio agli inizi della teoria. Sia H un sottogruppo arbitrario del gruppo finito G e sia χ un carattere del sottogruppo H (non necessariamente irriducibile). Sia χ′ la funzione su G che coincide con χ su H ed è zero sul complementare di H. Salvo che in casi molto speciali, χ′ non sarà una costante sulle classi coniugate e perciò non sarà una funzione di classe. Sia
La funzione χ* è ovviamente una funzione di classe e si può dimostrare che essa è un carattere, che viene chiamato il carattere ‛indotto' dal carattere χ di H. Un modo di provare che essa è un carattere consiste nel costruire una rappresentazione di cui essa è un carattere, il che si può fare nel modo seguente: sia L una rappresentazione di cui χ è un carattere. Indichiamo con ℋ lo spazio vettoriale di tutte le funzioni f da G allo spazio vettoriale ℋ(L) tali che f (hx) = Lh(f (x)) per tutte le h in H e tutte le x in G. Per ogni x in G, sia ULx l'operazione che porta ogni f di Η nell'immagine di f per la traslazione destra definita da x: ULx(f)(y) = f (yx). E chiaro che ULx(f) appartiene a ℋ e che x → ULx è una rappresentazione. Un facile calcolo mostra che il carattere di UL è (χL)* come l'abbiamo definito dianzi. La rappresentazione UL si chiama la rappresentazione di G indotta da L. È, chiaro che (χ1 + χ2)* = χ1* + χ2*, cosicché l'operazione d'induzione commuta con l'operazione di somma diretta e un carattere indotto non può mai essere irriducibile a meno che non lo sia il carattere che lo induce. Quando χ è irriducibile, χ* può esserlo oppure no. Per esempio, quando χ è la rappresentazione banale del sottogruppo identità, χ* è il carattere della rappresentazione regolare. D'altra parte, come vedremo dettagliatamente in seguito, esistono molti gruppi finiti non commutativi (per esempio tutti quelli nilpotenti) per i quali ogni carattere irriducibile ha la forma χ* per un carattere ‛a una dimensione' di qualche sottogruppo. Un'altra facile regola formale è che (χ1 × χ2)* = χ1* × χ2*, ove χ1 e χ2 sono caratteri di sottogruppi H1 e H2 dei gruppi finiti G1 e G2.
Poiché la rappresentazione indotta UL di G non è necessariamente irriducibile anche quando L è una rappresentazione irriducibile del sottogruppo H, nasce il problema di decomporre UL e in particolare di determinare il numero di volte, m(UL, M), in cui una data rappresentazione irriducibile M di G appare quando UL sia scritta come una somma diretta di rappresentazioni irriducibili. Il famoso teorema di reciprocità di Frobenius afferma che m(UL, M) è uguale al numero di volte che L appare quando la rappresentazione M è ‛ristretta' ad H ed è scritta come somma diretta di rappresentazioni irriducibili di H. Quindi le operazioni dell'indurre e del restringere sono in un certo senso duali. Il teorema di reciprocità di Frobenius si può dimostrare anche applicando le relazioni di ortogonalità alla definizione di χ*, ove χ = χL.
Quando G è un prodotto semidiretto di un gruppo normale commutativo N e di un altro sottogruppo H, è possibile utilizzare la nozione di carattere indotto per costruire tutti i caratteri irriducibili di G quando siano noti quelli di H e di certi suoi sottogruppi. Questo procedimento può quindi essere usato in modo induttivo per determinare in molti casi tutti i caratteri irriducibili. Per ogni carattere χ di dimensione 1 di N e ogni h in H, sia [χ]h il carattere di dimensione 1 n ???14??? χ(hnh-1); cioè il trasformato di χ mediante il duale dell'automorfismo n ???14??? hnh-1. Sia ℴχ l'orbita di χ, cioè l'insieme di tutti i [χ]h per h che varia in H; sia Hχ il sottogruppo di tutti gli h in H tali che [χ]h = χ. Sia C un sottoinsieme di Í che ha uno e un solo elemento in ciascuna orbita. Per ogni χ ∈ C e ogni carattere irriducibile ρ di Hχ, indichiamo con χρ la funzione n, h ???14??? χ(n) ρ(h). Si può dimostrare che χρ è un carattere, che (χρ)* è irriducibile e che ogni carattere irriducibile di G può ottenersi in questo modo. Inoltre, se χ1 e χ2 stanno in C, risulta che (χ1ρ1)* = (χ2ρ2)* se, e soltanto se, χ1 = χ2 e = ρ1 = ρ2.
Esiste una generalizzazione del risultato precedente circa i prodotti semidiretti che si applica quando N non è necessariamente un sottogruppo commutativo normale di G e l'estensione non si spezza. Il gruppo quoziente G/N sostiene il ruolo di H, ma ci si riduce a studiare non le rappresentazioni irriducibili dei sottogruppi di H, bensì le rappresentazioni ‛proiettive' irriducibili per certi ‛moltiplicatori' σ. Per definizione, una ‛rappresentazione proiettiva' del gruppo G è una funzione x ???14??? Vx che manda G nelle trasformazioni lineari non singolari di uno spazio vettoriale ℋ(V), tale che Vxy = σ(x, y)VxVy per tutti gli x e y in G e per una funzione a valori complessi non nulli x, y → σ(x, y) definita su G × G. La funzione σ si chiama il ‛moltiplicatore' della rappresentazione proiettiva V. Se V è una rappresentazione proiettiva con moltiplicatore σ e ϕ è una funzione complessa arbitraria che non si annulla mai su G, l'applicazione x ???14??? ϕi(x)Vx è una rappresentazione proiettiva con moltiplicatore σ1, ove
σ1(x, y) = σ(x, y)ϕ(x, y)/ϕ(x)ϕ(y).
Due moltiplicatori σ e σ1 legati fra di loro in questo modo si dicono simili. Quando σ e σ1 sono simili, la teoria delle rappresentazioni proiettive con moltiplicatore σ coincide essenzialmente con la teoria delle rappresentazioni proiettive con moltiplicatore σ1. Quindi basta considerare soltanto un moltiplicatore in ogni classe di similitudine. Quando G è finito, ogni moltiplicatore è simile a uno i cui valori assoluti hanno tutti modulo uno. Il procedimento induttivo indicato dianzi cade quando la serie di Jordan-Hölder del gruppo finito contiene gruppi semplici non commutativi. Trovare i caratteri irriducibili di tali gruppi può rivelarsi un problema difficile. Esso fu risolto, agli albori della teoria, per gruppi come il gruppo simmetrico di n lettere e i gruppi classici SL(2, ℱ) e GL(2, ℱ), dove ℱ è un corpo finito. Si dovette tuttavia attendere fino al 1955 perché i caratteri irriducibili di GL(n, ℱ) fossero determinati da J. A Oreen, grazie anche a importanti ricerche anteriori di R. Steinberg. Per molti altri gruppi classici finiti, la questione non è ancora stata risolta ed è uno dei problemi di rilevante interesse attuale.
Nel 1947, R. Brauer dimostrò il seguente importante teorema generale. Se χ è un carattere arbitrario di un gruppo finito G, χ è una combinazione lineare finita con coefficienti interi (positivi e negativi) con caratteri indotti da caratteri di dimensione 1 di certi sottogruppi. Inoltre i sottogruppi possono sempre essere presi del tipo H1 × H2, ove H1 è ciclico e H2 ha per ordine la potenza di un numero primo. Questo teorema risulta equivalente a un altro, che si è dimostrato di grande importanza nelle recenti ricerche sui gruppi semplici menzionati nel cap. 4. Questo teorema equivalente afferma che una funzione f a valori complessi sul gruppo finito G è un carattere se, e soltanto se, è costante sulle classi coniugate ed è un carattere quando la si restringa a un qualsiasi sottogruppo del tipo H1 × H2, ove H1 è ciclico e H2 ha ordine uguale alla potenza di un numero primo. La prima forma di questo teorema ha importanti conseguenze nella teoria analitica dei numeri e fu congetturata da E. Artin nel 1924 proprio in vista di queste applicazioni. Un corollario che riveste notevole importanza per la teoria generale delle rappresentazioni dei gruppi può essere enunciato nel modo seguente: sia n il minimo comune multiplo degli ordini degli elementi di un gruppo finito G. Sia ℱ il più piccolo corpo che contiene i numeri razionali e tutte le radici n-esime dell'unità. Ogni rappresentazione di dimensione finita di G è equivalente a una rappresentazione mediante matrici i cui elementi stanno tutti in ℱ.
La teoria delle rappresentazioni dei gruppi finiti su corpi diversi da quello dei numeri complessi è più semplice quando il corpo ha caratteristica zero, cioè quando 1 + 1 + ... + 1 non è mai nullo. Se 1 + 1 + ... + 1 è zero, il numero minimo di termini per i quali questa condizione è soddisfatta è un numero primo p, chiamato caratteristica del corpo. Supponendo ℱ di caratteristica zero (o più in generale supponendo che la caratteristica non divida l'ordine di G), si può ancora provare che ogni rappresentazione di dimensione finita è somma diretta di rappresentazioni irriducibili e che esiste soltanto un numero finito di rappreséntazioni irriducibili; di fatto il numero di queste non supera il numero delle classi coniugate. Si possono inoltre introdurre caratteri e dimostrare che una rappresentazione di dimensione finita è univocamente determinata dal suo carattere.
Sia ℱ un corpo di caratteristica zero. Una rappresentazione irriducibile di G mediante matrici n × n con elementi in ℱ può diventare riducibile se gli elementi di ℱ vengono considerati come elementi di un sopracorpo ℱ′ contenente ℱ. Se la rappresentazione è irriducibile in ogni corpo ℱ′ estensione di ℱ, essa e il suo carattere si dicono ‛assolutamente irriducibili'. Si dimostra che è sempre possibile immergere ℱ come sottocorpo di un corpo ℱ′ in modo che: a) ℱ′ abbia dimensione finita se considerato come spazio vettoriale su ℱ; b) ogni rappresentazione irriducibile di G sul corpo ℱ′ sia assolutamente irriducibile. Il corpo ℱ′ dipende naturalmente da G e viene chiamato ‛corpo di spezzamento' di ℱ e G. A meno di isomorfismi di corpi, i caratteri irriducibili di un gruppo sopra un corpo di spezzamento sono sempre uguali ai caratteri irriducibili sul corpo dei numeri complessi. Il nuovo problema principale consiste quindi nel collegare i caratteri irriducibili su ℱ con quelli su un corpo di spezzamento ℱ′. Sia G il gruppo di tutti gli automorfismi del corpo ℱ′, che lasciano invariato ogni elemento di ℱ - il cosiddetto gruppo di Galois di ℱ′ su ℱ. Per ogni carattere irriducibile χ di G su ℱ′ e ogni α ∈ G, la funzione x ???14??? α(χ(x)) sarà ancora un carattere che potrà o no coincidere con χ e che si chiama ‛coniugato' di χ. Un teorema fondamentale dovuto a I. Schur afferma che i caratteri irriducibili di G su ℱ corrispondono in modo biunivoco alle classi di coniugio dei caratteri irriducibili di G su ℱ′. Inoltre, il carattere su ℱ corrispondente a una data classe di caratteri su ℱ′ è un multiplo intero positivo della somma dei caratteri in questa classe. L'intero positivo in questione si chiama l'‛indice di Schur', per il corpo ℱ, dei caratteri assolutamente irriducibili nella classe. La determinazione di tale classe nei casi concreti rappresenta la maggiore difficoltà della teoria. Un altro corollario del teorema di Brauer, menzionato dianzi, è che il problema della determinazione dell'indice di Schur si può ridurre al caso in cui G è un gruppo risolubile di un tipo speciale.
Quando il corpo ℱ ha caratteristica p che divide l'ordine 0(G) del gruppo finito G, la teoria delle rappresentazioni di dimensione finita di G diventa molto più difficile e molto più complicata. Non è più possibile scrivere ogni rappresentazione di dimensione finita come somma diretta di rappresentazioni irriducibili e le rappresentazioni non sono più determinate univocamente dai loro caratteri.
Introducendo la nozione di rappresentazione quoziente, in modo più o meno ovvio, si può assegnare a ogni rappresentazione di dimensione finita un insieme di rappresentazioni irriducibili che possono essere considerate come un insieme di ‛componenti irriducibili'. La somma diretta di queste sarà tuttavia soltanto un elemento di una famiglia di rappresentazioni aventi queste componenti. Il carattere di una rappresentazione deve essere definito in modo più sottile che nella teoria classica e determina allora, e ne è a sua volta determinato, le classi di equivalenza delle componenti irriducibili (contate con opportuna molteplicità). In particolare esso è una funzione complessa e non una funzione con valori in ℱ. Il numero dei caratteri irriducibili distinti è minore del numero delle classi coniugate, in quanto è uguale al numero delle classi ‛p-regolari', cioè al numero delle classi coniugate i cui elementi hanno ordini non divisibili per p. Quando ℱ è ‛algebricamente chiuso', nel senso che esiste un x in ℱ tale che a0 + a1x ... + akxk = 0 per ogni scelta di a0, a1, ..., ak in ℱ, con ak ≠ 0 e k ≥ 1, ogni carattere irriducibile χ di G sul corpo dei numeri complessi definisce, in modo naturale, un carattere, non necessariamente irriducibile, di G su ℱ. Questo carattere su ℱ si può scrivere nella forma ΣY dYχ Y, ove i dYχ sono interi non negativi e Y varia fra i caratteri irriducibili su ℱ. I ‛numeri di decomposizione' dYχ sostengono un ruolo importante nella teoria, al pari degli ‛invarianti di Cartan' cY,Y′ = Σχ dYχdYχ′. Questi insiemi di caratteri irriducibili sono suddivisi in sottoinsiemi disgiunti chiamati blocchi, che hanno la proprietà che, per ogni χ, dYχ = 0 per tutti gli Y, a eccezione di quelli in un dato blocco, e, per ogni Y, dYχ = 0 per tutti i χ, a eccezione di quelli in un dato blocco. I fondamenti di questa teoria dei caratteri e delle rappresentazioni sopra corpi aventi per caratteristica un numero primo (corpi modulari) furono posti da Brauer e Nesbitt in due lavori pubblicati nel 1937 e 1941 e la teoria ebbe successivamente un ampio sviluppo a opera di Brauer e di altri. Il fatto che un carattere irriducibile sul corpo dei numeri complessi possa essere ulteriormente decomposto introducendo dei corpi modulari trasforma la teoria dei caratteri su tali corpi in una versione assai potente e raffinata della teoria classica, per quanto concerne la dimostrazione dei teoremi che riguardano la struttura dei gruppi finiti. Da un punto di vista storico, è interessante notare che Brauer era allievo di Schur e Schur, a sua volta, era allievo di Frobenius.
Sia G un gruppo finito e sia ℱ un corpo. L'insieme Aℱ (G) di tutte le funzioni da G a ℱ è uno spazio vettoriale su ℱ in modo ovvio e diventa un anello quando si definisca una ‛moltiplicazione' f, g ???14??? f * g mediante la formula f * g(x) = Σy∈Gf (xy-1)g(y). Aℱ(G) è dunque ciò che si chiama comunemente un'‛algebra lineare associativa' o semplicemente un'‛algebra'. In essa la moltiplicazione per elementi di ℱ commuta con l'operazione della moltiplicazione nell'anello. Essa prende il nome di ‛algebra di gruppo' del gruppo G. Esiste una teoria delle algebre lineari associative di dimensione finita, analoga, sotto molti aspetti, alla teoria delle algebre di Lie. Si ha in particolare una nozione di semisemplicità e un teorema secondo il quale un'algebra semisemplice è una somma diretta di algebre semplici. Ogniqualvolta la caratteristica ℱ non divide l'ordine di G, l'algebra di gruppo risulta essere semisemplice e le sue componenti semplici corrispondono in modo naturale biunivoco ai caratteri irriducibili di G su ℱ. Inoltre, una parte della teoria dei caratteri e delle rappresentazioni modulari può dedursi da teoremi più generali sulla struttura e sulle rappresentazioni delle algebre non semisemplici. In breve, esiste una stretta connessione fra la teoria delle rappresentazioni dei gruppi e la teoria delle algebre lineari associative.
8. Misura di Haar e rappresentazioni unitarie di gruppi separabili localmente compatti in uno spazio di Hilbert.
Sia G un gruppo separabile localmente compatto e sia ℬ la più piccola famiglia di sottoinsiemi di G che contiene gli insiemi chiusi ed è inoltre dotata delle due seguenti proprietà: a) se E è in ℬ, l'insieme G−E di tutti gli x che non sono in E è ancora un elemento di ℬ; b) se E1, E2, ..., En, ... sono elementi di ℬ, l'unione E1 ⋃ E2 ⋃ ... ⋃ En ⋃ ... di questi insiemi è ancora un elemento di ℬ. Gli elementi di ℬ si chiamano ‛sottoinsiemi di Borel' di G. Nel 1933 A. Haar dimostrò il seguente teorema di notevole importanza. Esiste sempre una funzione μ su ℬ avente per valori dei numeri reali non negativi e ∞, che è una misura, nel senso che μ(E1 ⋃ E2 ⋃ ... ⋃ En ⋃ ...) = μ(E1) + μ(E2) + ... + μ(En) + ..., ogniqualvolta gli Ej sono disgiunti; essa è inoltre ‛localmente finita', nel senso che μ(E) 〈 ∞ ogniqualvolta E è compatto, è ‛invariante a destra', nel senso che μ(Ex) = μ(E) per tutti gli E in ℬ e tutti gli in G, ed è ‛non banale', nel senso che μ(G) ≠ 0. Tre anni più tardi J. L. von Neumann mostrò che due misure siffatte sono multipli costanti l'una dell'altra, cosicché la ‛misura di Haar invariante a destra è essenzialmente unica'. Nello stesso anno A. Weil dimostrò che, formulando opportunamente il teorema, si può eliminare l'ipotesi di separabilità. Tratteremo tuttavia qui soltanto il caso in cui G è separabile. Quando G è il gruppo additivo della retta reale, la costante arbitraria può essere scelta in guisa tale che la misura di Haar di un intervallo sia esattamente la lunghezza di quell'intervallo; la misura di Haar si riduce così alla misura di Lebesgue. La teoria di Lebesgue dell'integrazione fu estesa agli spazi astratti di misura poco prima del 1920; applicando questa estensione alla misura di Haar μ in un gruppo G, si può dare un significato alla notazione ∫ f(x) dμ(x) per ogni funzione f a valori reali o complessi che sia una ‛funzione di Borel' tale che ∣ f(x) ∣ non sia ‛troppo grande'. Si dice che f è una ‛funzione di Borel se f-1(ℴ) è un insieme di Borel ogniqualvolta ℴ è aperto; una funzione di Borel si chiama ‛funzione semplice' se assume soltanto un numero finito di valori distinti. Una funzione semplice può sempre essere scritta in modo univoco nella forma f(x) = c1ϕE1(x) + ... + cnϕEn(x), ove E1, E2, ..., En sono insiemi di Borel disgiunti, ϕEj(x) è la funzione che è 1 in Ej e 0 in G − Ej e i cj sono costanti distinte, reali o complesse. Quando f è una funzione semplice, si definisce ∫ f(x) dμ(x) come c1μ(E) + ... + cnμ(En). Quando f è una funzione di Borel non negativa, si prende per definizione ∫ f(x) dμ(x) uguale all'estremo superiore dei numeri ∫ g(x) dμ(x) al variare di g nella famiglia di tutte le funzioni semplici non negative tali che f(x) ≥ g(x) per ogni x. Se f è una funzione di Borel arbitraria, si dice che f è ‛sommabile' se
∫ ∣ f(x) ∣ dμ(x) 〈 ∞.
Ogni funzione f complessa sommabile può essere scritta nella forma (f1 − f2) + i(f3 − f4), ove f1, f2, f3 e f4 sono funzioni di Borel sommabili non negative; in tal caso si definisce ∫ f(x) dμ(x) = ∫ f1(x) dμ(x) − ∫ f2(x) dμ(x) + i ∫ f3(x) dμ(x) − i ∫ (f4(x) dμ(x)), dopo aver dimostrato che il termine al secondo membro resta inalterato comunque si operino su f le decomposizioni indicate. Quando G è un gruppo finito o un gruppo discreto numerabile, la costante arbitraria nella misura di Haar μ può essere scelta in guisa tale che μ(E) sia il numero degli elementi nell'insieme E, sicché ∫ f(x) dμ(x) è, per ogni funzione sommabile f, Σx∈G f(x). Segue subito dall'esistenza della misura di Haar invariante a destra che esiste anche una misura di Haar invariante a sinistra. Tuttavia la misura di Haar invariante a sinistra non è necessariamente invariante a destra e viceversa. Quei gruppi per i quali le misure di Haar invarianti a destra e a sinistra coincidono si dicono ‛unimodulari'. Fra essi si trovano i gruppi compatti, i gruppi discreti infiniti numerabili, i gruppi di Lie semisemplici e, naturalmente, i gruppi commutativi localmente compatti.
Se G è compatto (e solo in questo caso), la misura di Haar di G è finita e la costante arbitraria può essere scelta in modo tale che μ(G) = 1. In questo caso ogni funzione di Borel limitata (e in particolare ogni funzione continua) è sommabile rispetto a μ. Sia V una rappresentazione di dimensione finita del gruppo compatto separabile G sui numeri complessi tale che x ???14??? Vx sia una funzione continua. Quando G è finito, si dimostra che lo spazio vettoriale ℋ( V) può essere dotato di un prodotto interno definito positivo invariante; a tal uopo si parte da un prodotto interno definito positivo arbitrario, ϕ, ψ ???14??? [ϕ, ψ], e si pone per definizione [ϕ, ψ]10 = Σx∈G [Vx(ϕ), Vx(ψ)]. Se G è compatto ma non finito, per giungere allo stesso risultato basta sostituire la somma precedente con un integrale rispetto alla misura di Haar. Quindi, ogni rappresentazione continua di dimensione finita di un gruppo separabile è una somma diretta di rappresentazioni irriducibili. Il carattere di una rappresentazione di dimensione finita viene definito proprio come per i gruppi finiti e determina ancora la rappresentazione a meno di una equivalenza. Inoltre, le importanti relazioni di ortogonalità per i caratteri irriducibili si estendono al caso compatto, purché si utilizzi l'integrazione rispetto alla misura di Haar in luogo delle sommatorie sugli elementi del gruppo. Specificamente, se χ1 e χ2 sono caratteri irriducibili, 1/μ(G) ∫ χ1(x) -χ2(x) dμ(x) = 0 o χ1(e) secondo che χ1 ≠ χ2 oppure χ1 = χ2. In termini generali, la teoria delle rappresentazioni dei gruppi compatti separabili si sviluppa in modo parallelo a quella dei gruppi finiti: la differenza sostanziale sta nel fatto che, se il gruppo non è finito, si ha un'infinità numerabile di caratteri irriducibili distinti. Corrispondentemente, per avere una nozione analoga a quella di rappresentazione regolare - e, più generalmente, di rappresentazione indotta - si devono considerare rappresentazioni che non hanno dimensione finita.
In generale, sia μ una misura di Haar invariante a destra nel gruppo separabile localmente compatto G e sia ℒ²0(G, μ) l'insieme di tutte le funzioni f a valori complessi su G tali che ∫ ∣ f(x) ∣2 dμ(x) 〈 ∞. È noto dalla teoria dell'integrale di Lebesgue che ℒ²0(G, μ) è uno spazio vettoriale rispetto alle operazioni ovvie e che -fg è sommabile per tutte le f e g in ℒ²0(G, μ). Si verifica che la formula (f•g) = ∫ f(x)à(x) dμ(x) definisce un prodotto interno in ℒ²0(G, μ) il quale non è definito positivo, solo perché (f•f) può essere zero senza che f sia identicamente zero. Tuttavia questo accade solo se f si trovi nel sottospazio vettoriale di tutte le f che sono zero a eccezione che in un sottoinsieme di misura di Haar zero. Per questo motivo identificheremo f e f′ ogniqualvolta f − f′ si trovi in questo sottospazio di ‛funzioni nulle' e ci riferiremo allo spazio quoziente che indicheremo con ℒ2(G, μ). È opportuno, e di solito del tutto pacifico, usare lo stesso simbolo sia per un elemento di ℒ²0(G, μ) che per la sua immagine in ℒ2(G, μ) e non succede niente di grave se si confondono questi due oggetti. Per ogni x in G e ogni f in ℒ2(G, μ), sia Ux(f)(y) = f(yx). Ogni Ux è una trasformazione lineare di ℒ2(G, μ) in se stesso e x ???14??? Ux è una rappresentazione di G. Quando G è finito, essa si riduce alla rappresentazione regolare definita precedentemente e pertanto verrà chiamata in tutti i casi rappresentazione lineare'.
Il prodotto interno definito positivo, f, g ???14??? (f•g) = ∫ f(x)g(x) dμ(x), in ℒ2(G, μ), fa di questo spazio quello che oggi si chiama uno ‛spazio di Hilbert separabile'. Dato uno spazio vettoriale V sui numeri complessi, prende il nome di ‛norma' una funzione f ???14??? ∥ f ∥ che manda lo zero nello zero e associa un numero reale positivo a ogni elemento non nullo f di V in modo tale che ∥ λf1 ∥ = ∣ λ ∣ ∥ f1 ∥ e ∥ f1 + f2 ∥ ≤ ∥ f1 ∥ + ∥ f2 ∥ per tutti gli f1 e f2 in V e ogni numero complesso λ. Data una norma, si definisce la distanza fra due elementi f1 ef2 prendendola per definizione uguale a ∥ f1 − f2 ∥ e si dice che la successione f1, f2, ..., fn, ... ‛converge' all'elemento f, o ‛ha per limite' f, se la successione di numeri reali {∥ fj − f ∥} converge a 0 nel senso usuale. Si scrive f = g1 + g2 + ... + gn + ... se fn converge a f avendo posto fn = g1 + g2 + ... + gn. Quindi, in uno ‛spazio vettoriale normato', cioè in uno spazio con una norma, si può dare un significato alle somme infinite. Uno spazio vettoriale normato diventa uno spazio topologico di Hausdorff se si prendono gli insiemi chiusi nel modo seguente: un insieme F si dice chiuso se contiene il limite di ogni successione di elementi dotata di limite. Supponiamo che la successione f1, f2, ..., fn, ... converga a f. È chiaro allora che, dato un qualsiasi numero reale positivo ε, esiste un intero positivo N tale che ∥ fn − fm ∥ ≤ ε ogniqualvolta n e m siano ambedue più grandi di N. Una successione dotata di questa poprietà si chiama ‛successione di Cauchy'. Uno spazio vettoriale normato si dice ‛completo' o ‛spazio di Banach' se ogni successione di Cauchy ha un limite. Se f, g ???14??? [f•g] è un prodotto interno definito positivo nello spazio vettoriale complesso V, posta per definizione ∥ f ∥ = √-(-f- -•- -f), si dimostra che f ???14??? ∥ f ∥ è una norma e che ∣ [f•g] ∣ ≤ ∥ f ∥ • ∥ g ∥ per ogni f e ogni g. Uno spazio di Banach la cui norma può essere ottenuta in questo modo da un prodotto interno definito positivo si chiama ‛spazio di Hilbert'. Uno spazio vettoriale normato dotato di questa proprietà si chiama ‛spazio pre-hilbertiano'. È facile dimostrare che ℒ2(G, μ) è uno spazio pre-hilbertiano rispetto al prodotto interno f, g ???14??? ∫ f(x)à(x) dμ(x) e più profondo è il teorema che ℒ2(G, μ) è completo, e quindi uno spazio di Hilbert.
Siano ℋ1 e ℋ2 due spazi di Hilbert con prodotti interni (f•g)1 e (f′•g′)2. Una trasformazione lineare bigettiva W da ℋ1 a ℋ2 si dice ‛unitaria' se (W(f)•W(g))2 = (f•g)1 per tutti gli f e g in ℋ1. In genere si omettono gli indici che distinguono i diversi prodotti interni, a meno che questi ultimi non siano definiti sullo stesso spazio vettoriale. Chiaramente tutti gli operatori Ux nella rappresentazione regolare di G sono operatori unitari nello spazio di Hilbert ℒ2(G, μ) e segue facilmente dalla teoria dell'integrale di Lebesgue che x ???14??? (Ux(f)•g) è una funzione di Borel su G per ogni f e ogni g in ℒ2(G, μ). In tutta generalità, una ‛rappresentazione unitaria' di un gruppo topologico G è per definizione un omomorfismo x ???14??? Vx di G nel gruppo di tutti gli operatori unitari di uno spazio separabile di Hilbert ℋ(V) su se stesso, tale che x ???14??? (Vx(f)•g) sia una funzione di Borel per tutti gli f e g in ℋ(V). Si dimostra che, se x ???14??? Vx è una rappresentazione unitaria, x ???14??? Vx(f) è una funzione continua da G a ℋ(V). Naturalmente si possono considerare rappresentazioni unitarie in spazi di Hilbert non separabili, ma non lo faremo in questo articolo. Segue da quanto abbiamo detto che la rappresentazione regolare di un gruppo arbitrario localmente compatto e separabile è una rappresentazione unitaria e che ogni rappresentazione continua di dimensione finita di un gruppo compatto è equivalente a una rappresentazione unitaria. La teoria delle rappresentazioni unitarie dei gruppi di Lie localmente compatti e separabili include dunque, e generalizza in modo naturale, la teoria delle rappresentazioni continue di dimensioni finite di gruppi compatti e la teoria delle rappresentazioni di dimensione finita arbitraria di gruppi finiti sul corpo dei numeri complessi.
Molti dei concetti della teoria delle rappresentazioni di dimensione finita sul corpo dei complessi si possono estendere immediatamente e in modo ovvio alla teoria delle rappresentazioni unitarie di dimensione non necessariamente finita. È tuttavia necessaria qualche modifica. Per esempio, un sottospazio lineare di uno spazio di Hilbert è esso stesso uno spazio di Hilbert se, e soltanto se, esso è ‛chiuso' rispetto alla topologia dello spazio in questione. Conseguentemente, quando si definiscono le sottorappresentazioni, si considerano soltanto sottospazi invarianti ‛chiusi'. Si dice ‛irriducibile' una rappresentazione unitaria se essa non ammette nessun sottospazio invariante proprio ‛chiuso'. Le rappresentazioni V1 e V2 si dicono ‛equivalenti' se esiste un'applicazione unitaria W di ℋ(V1) su ℋ(V2) tale che WV¹xW-1 = V²x per tutti gli x in G. Più in generale una trasformazione lineare continua A da ℋ(V1) a ℋ(V2) si dice un ‛operatore di allacciamento' (o di ‛intrecciamento') per V1 e V2 se AV¹x = V²xA per tutti gli x in G. Dato un operatore di allacciamento A non nullo, indichiamo con NA l'insieme di tutti gli f con A(f) = 0 e sia RA l'insieme di tutti gli A(f). NA e RA sono sottospazi invarianti di ℋ(V1) e ℋ(V2) rispettivamente. Ne segue che NA⊥ e ÒA sono sottospazi chiusi invarianti, ove NA⊥ - ‛complemento ortogonale' di NA - è l'insieme di tutti gli f tali che (f•g) = 0 per tutti i g in NA; ÒA è la chiusura di RA. Si può dimostrare che le sottorappresentazioni definite da NA⊥ e ÒA sono equivalenti nel senso definito or ora; ne segue che due rappresentazioni unitarie di dimensioni finite sono equivalenti nel senso del cap. 7 se, e soltanto se, sono equivalenti come rappresentazioni unitarie. Ne segue anche che due rappresentazioni unitarie ammettono operatori di allacciamento non nulli se, e soltanto se, qualche sottorappresentazione propria di una è equivalente a qualche sottorappresentazione propria dell'altra.
Sia ℋ1, ℋ2, ..., ℋn, ... una successione infinita di spazi di Hilbert e sia ℋ l'insieme di tutte le successioni ϕ1, ϕ2, ..., ϕn, ..., ove ϕj ∈ ℋj e
∥ ϕ1 ∥2 + ∥ ϕ2 ∥2 + ... + ∥ ϕn ∥2 + ... 〈 ∞.
Si può dimostrare che ℋ diventa uno spazio di Hilbert quando si definisca
λ(ϕ1, ϕ2, ..., ϕn, ...) = (λϕ1, λϕ2, ..., λϕn, ...);
(ϕ1, ϕ2, ..., ϕn, ...) + (ψ1, ψ2, ..., ψn, ...) =
= (ϕ1 + ψ1, ϕ2 + ψ2, ..., ϕn + ψn, ...);
(ϕ1, ϕ2, ..., ϕn, ...) • (ψ1, ψ2, ..., ψn, ...) =
= (ϕ1 • ψ1) + (ϕ2 • ψ2) + ... + (ϕn • ψn) + ... .
Questo spazio di Hilbert si chiama somma diretta, ℋ1 ⊕ ℋ2 ⊗ ... ⊕ ℋn ⊕ ..., degli spazi ℋj. In base a questa nozione si può definire in modo ovvio nel caso unitario la nozione di somma diretta di un'infinità numerabile di rappresentazioni. Se V1 ⊕ V2 ⊕ V3 ⊕ ... ⊕ Vn ⊕ ... è equivalente a U1 ⊕ U2 ⊕ U3 ⊕ ... ⊕ Un ⊕ ... ove tutte le Vj e le Uj sono ‛irriducibili', è facile provare che esiste una permutazione π degli interi positivi tale che Vj e Uπ(j) siano equivalenti per ogni j. Sfortunatamente, a eccezione del caso in cui G è compatto, è piuttosto insolito che una rappresentazione unitaria di dimensione infinita sia equivalente a una somma diretta di rappresentazioni irriducibili. È necessaria qui una teoria della riduzione più sofisticata in cui l'integrazione sostituisce la somma. Illustreremo ora questa teoria con qualche maggiore dettaglio.
Essa è particolarmente semplice nel caso speciale in cui il gruppo G è compatto. In tal caso ogni rappresentazione unitaria irriducibile è di dimensione finita e ogni rappresentazione unitaria può scriversi in uno, ed essenzialmente un sol modo, come somma diretta di rappresentazioni irriducibili. Inoltre, la rappresentazione regolare si decompone in rappresentazioni unitarie irriducibili, in modo che ogni rappresentazione unitaria irriducibile compare, in tale decomposizione, con una molteplicita uguale alla sua dimensione. Questo risultato sulla struttura della rappresentazione regolare, insieme al fatto che le sue componenti irriducibili sono di dimensione finita, è il contenuto essenziale del celebre teorema di Peter-Weyl dimostrato da Peter e H. Weyl nel 1927 nel caso speciale dei gruppi di Lie compatti. A quell'epoca non era ancora stato stabilito il teorema generale di Haar, ma si sapeva come definire un procedimento d'integrazione invariante per funzioni sui gruppi di Lie con i metodi della geometria differenziale. Come fu rilevato dallo stesso Haar, i risultati di Peter e Weyl possono estendersi immediatamente al caso generale, non appena sia disponibile una misura invariante. Tale misura fu usata per la prima volta per la teoria delle rappresentazioni dei gruppi da Schur, che nel 1924 se ne servì per lo studio delle rappresentazioni di certi gruppi compatti di Lie. Tuttavia, già nel lontano 1897 essa era stata usata da Hurwitz in questioni di teoria degli invarianti.
Le rappresentazioni continue irriducibili di dimensione finita di gruppi di Lie connessi, compatti o non compatti, possono essere studiate passando alle algebre di Lie dei gruppi. Infatti, se t ???14??? ϕ(t) è un sottogruppo a un parametro del gruppo e x ???14??? Vx è una rappresentazione continua di dimensione finita, t ???14??? V῍(t) è una rappresentazione continua di dimensione finita del gruppo additivo della retta e, come tale, può essere scritta in modo unico nella forma t ???14??? eTϕ, ove T῍ è una trasformazione lineare in ℋ(V). L'applicazione ϕ ???14??? T῍ risulta essere una rappresentazione dell'algebra di Lie LG, nel senso che Tλ1ϕ1+λ2ϕ2 = λ1T῍1 + λ2T῍2 e T[ϕ1ϕ2] = Tϕ1Tϕ2 per tutti i ϕ1 e ϕ2 in LG e tutti i numeri reali λ1 e λ2. Quando G è semplicemente connesso, il problema di trovare le sue rappresentazioni continue irriducibili può così interamente ridursi a un analogo problema per le algebre di Lie. Questo problema venne risolto nel 1913 e 1914 da É. Cartan per tutte le algebre di Lie semplici. In un'importante serie di lavori che apparvero nel 1924 e 1925, Weyl completò ed estese l'analisi di Cartan usando l'integrazione sul gruppo e operando direttamente con il gruppo stesso. Il punto essenziale è che esiste sempre un sottogruppo chiuso commutativo A - il cosiddetto sottogruppo di Cartan - tale che ogni rappresentazione irriducibile di G è determinata in modo univoco dalla sua restrizione ad A (restrizione che di solito è riducibile), in quanto A interseca ogni classe coniugata in G. Le rappresentazioni irriducibili di A sono note in modo ovvio (e tutte di dimensione 1) ed è possibile descrivere in modo elegante quali combinazioni a coefficienti interi positivi di tali rappresentazioni irriducibili appaiono come restrizioni di rappresentazioni irriducibili di G.
Come per i gruppi finiti, si può dimostrare che una rappresentazione unitaria irriducibile di un gruppo topologico ‛commutativo' ha necessariamente dimensione 1 e quindi è del tipo x ???14??? χ(x)I, ove I è l'identità di uno spazio a una dimensione e x ???14??? χ(x) è un omomorfismo continuo del gruppo G nel gruppo di tutti i numeri complessi di modulo 1. Tali funzioni si chiamano ‛caratteri continui a una dimensione' (o più semplicemente ‛caratteri' quando non vi sia pericolo di creare confusione terminologica). Come nel caso finito, il prodotto di due caratteri è un carattere e l'insieme G di tutti i caratteri è un gruppo. Diremo che un sottoinsieme ℴ di Ø è ‛aperto' se per ogni χ0 in ℴ esiste un numero positivo ε e un sottoinsieme compatto C di G tale che, se ∣ χ0(x) -_χ(x) − 1 ∣ 〈 ε per tutti gli x in C, risulta allora che χ ∈ ℴ. Si può allora dimostrare che Ø è separabile e localmente compatto quando lo è G. Inoltre Ø è compatto ogniqualvolta G è discreto e discreto ogniqualvolta G è compatto. Come nel caso finito, ciascun x in G definisce un elemento fx di Ø mediante la formula fx(χ) = χ(x), cosicche x ???14??? fx determina un omomorfismo di G in Ø. Mediante il teorema di Peter-Weyl, L. Pontrjagin riuscì a stabilire nel 1934 il suo famoso teorema di dualità per gruppi commutativi localmente compatti, secondo il quale l'applicazione x ???14??? fx fx è una bigezione, esattamente come nel caso finito, e inoltre è continua e ha un inverso continuo. Pertanto x ???14??? fx stabilisce un isomorfismo tra G e Ø come gruppi topologici.
Un'altra dimostrazione, valida anche per gruppi non separabili, fu trovata un anno più tardi da E. R. van Kampen. Nel corso di queste dimostrazioni vennero stabiliti certi teoremi di struttura, il più importante dei quali afferma che ogni gruppo commutativo localmente compatto G ha un sottogruppo compatto K tale che G/K è discreto oppure è il prodotto diretto di un numero finito di copie del gruppo additivo della retta reale e di un gruppo G′ dotato di un sottogruppo siffatto K. Come nel caso finito, ponendo (χ1 × χ2)(x, y) = χ1(x)χ2(y), si ottiene un isomorfismo fra i gruppi topologici G1×G2 e Ø1 × Ø2. È ovvio che per ogni numero reale y, la funzione x ???14??? eixy = χy(x) è un carattere del gruppo additivo della retta reale; in tal modo si ottengono tutti i caratteri e l'applicazione y ???14??? χy è un isomorfismo del gruppo additivo della retta reale sul duale. Ne segue subito che l'applicazione y1, y2, ..., yn ???14??? χy1,y2,...,yn definita dalla formula χy1,y2,...,yn(x1, x2, ..., xn) = ei(x1y1+x2y2+...+xnyn) stabilisce un isomorfismo topologico del gruppo additivo delle n-uple di numeri reali sul suo duale. Se eiϑ1, e eiϑ2, sono numeri complessi arbitrari di modulo 1, l'applicazione n1, n2, ..., nk ???14??? ei(n1ϑ1 +...+ nkϑk) è un carattere del gruppo additivo delle k-uple di interi e in tal modo si ottengono tutti i caratteri. Dal teorema di dualità si può concludere che il duale del prodotto diretto di k copie del gruppo di tutti i numeri complessi di modulo 1 è il gruppo additivo delle k-uple di interi.
Sia G un arbitrario gruppo compatto separabile e fissiamo la misura di Haar μ in modo tale che μ(G) = 1. Il teorema di Peter-Weyl implica che ogni f in ℒ2(G, μ) può essere scritta in uno e un solo modo nella forma f(x) = Σχ∈ØCχχ(x), ove la convergenza va intesa rispetto alla norma nello spazio di Hilbert ℒ2(G, μ). Le relazioni di ortogonalità implicano che ∫ f(x)-χ(x) dμ(x) = Cχ e inoltre che ∫ ∣ f(x) ∣2 dμ(x) = Σχ∈Ø ∣ Cχ ∣2. Posto Cχ = C(χ) e ricordando che sommare sugli elementi di un gruppo discreto equivale a integrare nspetto a un'opportuna misura di Haar???42???, si giunge alla formula inversa
f(x) = ∫ C(χ)χ(x) d???42???(χ),
C(χ) = ∫ f(x)-χ(x) dμ(x),
con ∫ ∣ f(x) ∣2 dμ(x) = ∫ ∣ C(χ)2 d???42???(χ), ove la prima formula vale universalmente quando è interpretata come abbiamo precedentemente indicato ed è valida per funzioni C tali che ∫ ∣ C(χ) ∣ d???42???(χ) 〈 ∞. Nel caso particolare in cui G è il gruppo quoziente del gruppo additivo della retta reale per il sottogruppo chiuso dei multipli interi di 2π, il carattere più generale è x ???14??? e2πinx e le formule precedenti si riducono a quelle classiche che legano una funzione periodica localmente a quadrato sommabile con la successione dei suoi coefficienti di Fourier. Per gruppi compatti separabili generali qualsiasi, si conclude facilmente che l'applicazione f ???14??? C, con C(χ) = ∫ f(x) -χ- (-x-) dμ(x), definisce una applicazione unitaria dello spazio di Hilbert ℒ2(G, μ) nello spazio di Hilbert ℒ2(Ø, ???42???). La sua inversa è definita, almeno per tutte le funzioni C in un sottospazio denso di ℒ2(Ø, ???42???), dalla formula simile f(x) = ∫ f(x)χ(x) d???42???(χ). La simmetria espressa da questa formulazione suggerisce una generalizzazione al caso non compatto.
Sia ora G un gruppo commutativo separabile localmente compatto e sia μ una misura di Haar. Data una qualunque funzione f a valori complessi, sommabile rispetto a μ, sia ???43??? (x) = ∫ f(x)χ(x) dμ(x). È possibile dimostrare che le funzioni sommabili f in ℒ2(Ø, ???42???) costituiscono un sottospazio denso e che l'applicazione lineare F′ che manda f in ???43??? è un'applicazione continua di questo sottospazio denso su un sottospazio denso di ℒ2(Ø, ???42???); essa conserva anche le norme quando si scelga un'opportuna misura ???42??? di Haarin in Ø. Pertanto essa si può estendere in uno e un sol modo in un'applicazione unitaria di ℒ2(G, μ) su ℒ2(Ø, ???42???). Questa applicazione si chiama ‛trasformazione di Fourier', poichè, quando G è il gruppo additivo della retta reale, essa diventa la trasformazione di Fourier classica f(y) = ∫∞-∞ f(x) eixy dx. Per la stessa ragione, il teorema che afferma che l'applicazione è unitaria si chiama ‛teorema di Plancherel'.
È importante, e al tempo stesso interessante, vedere quale forma assume la rappresentazione regolare U di G quando, mediante la trasformazione di Fourier, la si esprima come una rappresentazione equivalente il cui spazio sia ℒ2(Ø, ???42???). Un calcolo diretto mostra che FUxF-1 applicato a χ ???14??? f(x) è la funzione χ ???14??? ???43???(χ)-χ(x); in altre parole tutti gli operatori FUxF-1 sono operatori di moltiplicazione in ℒ2(Ø, ???42???) e si può pensare alla rappresentazione regolare come a un integrale diretto o a una somma diretta continua dei caratteri -χ rispetto alla misura di Haar ???42???. Per comprendere questa interpretazione basta osservare cosa accade quando G è compatto e in tal caso Ø è discreto. Quando G non è compatto, si vede facilmente che U non ha sottorappresentazioni irriducibili.
L'interpretazione della rappresentazione regolare di G come ‛integrale diretto', rispetto a una misura di Haar, di tutti i caratteri in Ø suggerisce immediatamente la definizione di una classe più generale di rappresentazioni con un'interpretazione simile. Sia ν una misura arbitraria localmente finita in Ø e definiamo una rappresentazione unitaria Lν nello spazio di Hilbert ℒ2(Ø, ν) ponendo Lxνg(χ) ???14??? g(χ)-χ(x). Quando G è compatto si vede facilmente che Lν è la somma diretta di tutti i caratteri χ per i quali ν({χ}) ≠ 0, presi ciascuno con molteplicità 1. Più in generale, si può dimostrare che Lν1 e Lν2 sono equivalenti se, e soltanto se, le misure ν1 e ν2 hanno gli stessi insiemi di misura nulla, cosicché (per il teorema di Radon-Nikodyn) ciascuna può essere ottenuta dall'altra integrando una densità positiva. Si dirà allora che le misure sono ‛simili' o appartengono alla stessa ‛classe di misura'. L'interpretazione di Lν quando G è compatto suggerisce che più in generale Lν è, in un certo senso, ‛privo di molteplicità', che ogni rappresentazione priva di molteplicità è equivalente a una Lν e che infine ogni rappresentazione unitaria di un gruppo abeliano separabile localmente compatto G è una somma diretta di rappresentazioni prive di molteplicità. Queste considerazioni vaghe possono ancorarsi a fatti concreti. Sia U = L1 ⊕ L2 ⊕ ... ⊕ Ln dove le Lj sono rappresentazioni unitarie irriducibili di un gruppo G non necessariamente commutativo. Sia R(U, U) l'‛algebra commutante' di U, cioè l'anello di tutti gli operatori di intrecciamento di U con U. Una facile argomentazione mostra che quest'algebra commutante è commutativa se, e soltanto se, Li e Lj sono non equivalenti ogniqualvolta sia i ≠ j. Di conseguenza diremo che una rappresentazione unitaria arbitraria è ‛priva di molteplicità' se la sua algebra commutante è commutativa. Si dimostra allora che, se G è commutativo, ogni Lν è privo di molteplicità e che ogni rappresentazione unitaria priva di molteplicità è equivalente a un Lν. Indipendentemente dal fatto che G sia commutativo oppure no, si può dimostrare che, se L e M sono prive di molteplicità, L ⊕ L ⊕ ... ⊕ L k volte è equivalente a M ⊕ M ⊕ ... ⊕ M k′ volte se, e soltanto se, k = k′ e L è equivalente a M. Questo dà un ovvio significato coerente al fatto di avere ‛uniforme molteplicità' k e si può dimostrare che ogni rappresentazione unitaria di un gruppo abeliano localmente compatto e separabile è una somma diretta M∞ ⊕ M1 ⊕ M2 ⊕ ... ⊕ Mn ⊕ ..., ove alcuni termini possono mancare e ove Mj ha molteplicità uniforme j. Di fatto questa scomposizione può essere ottenuta in modo tale che gli addendi che in essa compaiono siano ‛disgiunti', nel senso che nessuna sottorappresentazione dell'uno sia equivalente a una sottorappresentazione dell'altro; pertanto gli Mj sono univocamente determinati.
Nel caso particolare in cui G è il gruppo additivo della retta reale, la teoria delle rappresentazioni unitarie di G è equivalente alla teoria di una classe di operatori lineari. Se A è una trasformazione lineare continua dello spazio di Hilbert separabile ℋ in se stesso, possiamo definire eiAt per tutti i numeri reali t come la somma della serie
Questa somma ha senso perché tutti gli operatori lineari continui formano uno spazio di Banach con ∥ A ∥ = estremo superiore di ∥ A(f) ∥ per ∥ f ∥ = 1. Si può dimostrare che t ???14??? eiAt è una rappresentazione unitaria di G se, e soltanto se, A è ‛autoaggiunto', nel senso che A = A*, ove A* è l'operatore definito univocamente dall'identità (A(f)•g) = (f•A*(g)) per tutti gli f e g nello spazio di Hilbert ℋ. Inoltre, t ???14??? eiAt e t ???14??? eiA′t sono equivalenti se, e soltanto se, esiste un operatore unitario W tale che WAW-1 = A′. Quando si estende la definizione di operatore autoaggiunto fino a includere nella categoria di questi operatori certi operatori discontinui (non limitati) i quali non sono definiti dappertutto, si può estendere corrispondentemente la definizione di eiAt, ottenendo così una corrispondenza biunivoca fra le classi di equivalenza di rappresentazioni unitarie del gruppo additivo della retta e la classe di equivalenza degli operatori autoaggiunti. Il fatto che ogni rappresentazione unitaria del gruppo additivo della retta reale possa essere posta nella forma t ???14??? eiAt, ove A è un operatore autoaggiunto, fu dimostrato nel 1930 da M. H. Stone ed è noto come ‛teorema di Stone'.
Quando i teoremi precedenti sulle rappresentazioni unitarie sono particolarizzati al caso del gruppo additivo della retta reale e sono reinterpretati come risultati sugli operatori autoaggiunti, essi danno il famoso teorema spettrale e la ‛teoria della molteplicità spettrale' a esso collegata. Il teorema spettrale per il caso particolare degli operatori continui (limitati) autoaggiunti fu scoperto da Hilbert e può considerarsi l'apice dei suoi studi decennali sulle equazioni integrali (1902-1912). I dettagli della teoria della molteplicità spettrale nel caso limitato vennero elaborati da Hahn e Hellinger nel periodo immediatamente successivo. L'estensione al caso non limitato fu sviluppata verso la fine del 1920 da von Neumann e Stone e si trova esposta in maniera esemplare nel trattato di Stone del 1932, Linear transformations in Hilbert space and their applications to analysis. Naturalmente a quell'epoca non erano ancora disponibili la misura di Haar e i teoremi di dualità di Pontrjagin e il fatto che esistesse un ‛teorema spettrale' per rappresentazioni unitarie per i gruppi commutativi localmente compatti non fu rilevato che intorno al 1945. Altri aspetti della teoria delle rappresentazioni unitarie dei gruppi compatti e dei gruppi commutativi localmente compatti erano già ben chiari verso la fine del 1930 e vennero esposti sistematicamente in due volumi fondamentali che apparvero rispettivamente nel 1940 e 1939: L'intégration dans les groupes topologiques et ses applications di A. Weil e Topological groups di L. Pontrjagin.
Abbiamo detto che una rappresentazione V di un gruppo compatto localmente separabile si chiama priva di molteplicità se la sua algebra commutante R(V, V) è commutativa. All'estremo opposto si trovano quelle rappresentazioni le cui algebre commutanti hanno i centri costituiti dagli operatori costanti. Tali rappresentazioni si chiamano ‛rappresentazioni primarie' o ‛rappresentazioni fattori'; questa terminologia deriva dal fatto che esse sono esattamente le algebre commutanti chiamate ‛fattori' da von Neumann e Murray nei loro lavori fondamentali su quelli che si chiamavano allora anelli di operatori e sono noti oggi come ‛algebre di von Neumann'. Si vede facilmente che una rappresentazione unitaria è una rappresentazione fattore se, e soltanto se, non è equivalente alla somma diretta di due sottorappresentazioni ‛disgiunte'. Questo implica che la somma diretta di rappresentazioni unitarie irriducibili mutuamente equivalenti è sempre una rappresentazione fattore e tali rappresentazioni fattori si dicono di ‛tipo I'. Si vede facilmente che una rappresentazione fattore è di tipo I se, e soltanto se, la sua algebra commutante è un fattore di tipo I nel senso definito da von Neumann e Murray nel primo lavoro su questo argomento, pubblicato insieme dai due autori nel 1936. Poiché si verifica facilmente che ogni algebra di von Neumann è l'algebra commutante di una rappresentazione unitaria di un gruppo discreto numerabile, la scoperta di von Neumann e Murray che esistono fattori non di tipo I implica che devono esistere rappresentazioni unitarie non di tipo I di certi gruppi discreti numerabili. Nella loro memoria del 1943, essi dimostrarono che la rappresentazione regolare di un gruppo discreto numerabile è una rappresentazione fattore di tipo II ogniqualvolta le classi coniugate sono infinite a eccezione di quella che contiene l'identità. Poiché ogni gruppo con rappresentazioni fattori non di tipo I ha anche rappresentazioni unitarie di dimensione infinita che sono irriducibili, questo fenomeno non si presenta per i gruppi compatti e i gruppi commutativi.
Di fatto esso non si presenta neanche per molti gruppi importanti che non sono né compatti né commutativi e per questi è possibile sviluppare una teoria della decomposizione e una teoria della molteplicità del tutto parallela a quella valida nel caso commutativo. Si dimostra anzitutto che le seguenti due condizioni sono equivalenti quando G è un gruppo localmente compatto: a) ogni rappresentazione fattore di G è di tipo I; b) ogni rappresentazione unitaria di G è una somma diretta di rappresentazioni prive di molteplicità. I gruppi che soddisfano l'una o l'altra di queste condizioni si dicono ‛gruppi di tipo I'. I gruppi separabili localmente compatti che sono di tipo I includono non soltanto i gruppi compatti e quelli commutativi, ma anche i gruppi di Lie connessi semisemplici, i ‛gruppi algebrici' reali (v. sotto, cap. 9) e un'ampia classe di gruppi di Lie connessi e risolubili (nella totalità dei gruppi di quest'ultimo tipo si trovano altresì gruppi che non sono di tipo I). D'altra parte, un gruppo discreto numerabile è di tipo I se, e soltanto se, ha un sottogruppo normale commutativo con quoziente finito. Quando G è di tipo I si può esprimere canonicamente ogni rappresentazione unitaria di G mediante rappresentazioni prive di molteplicità proprio come nel caso commutativo. Per quanto riguarda le rappresentazioni prive di molteplicità, si indica con Ø l'insieme di tutte le classi di equivalenza delle rappresentazioni unitarie irriducibili e si dimostra che è possibile isolare una famiglia di sottoinsiemi di Ø i quali si comportano come insiemi di Borel in Ø quando G è commutativo. A ogni misura finita ν definita sugli insiemi di Borel in Ø si associa una rappresentazione unitaria Lν di G priva di molteplicità mediante una specie d'integrazione. In questo modo si può ottenere ogni rappresentazione unitaria di G priva di molteplicità e ν ???14??? Lν stabilisce una corrispondenza biunivoca tra le classi di misura in Ø e le classi di equivalenza delle rappresentazioni prive di molteplicità di G, in modo completamente analogo alla teoria commutativa.
Quando G è un gruppo localmente compatto separabile, non di tipo I, si può decomporre la rappresentazione unitaria di G più generale come un ‛integrale diretto' di rappresentazioni fattori in un modo canonico e il problema essenziale diventa quello di studiare rappresentazioni fattori non di tipo I. Sotto molti aspetti queste si comportano come le rappresentazioni fattori di tipo I. Per esempio, due rappresentazioni fattori possono essere disgiunte, oppure una è l'equivalente di una sottorappresentazione dell'altra. Quando ciò accade, si dice che le rappresentazioni fattori sono ‛quasi equivalenti'. Si vede che la quasi equivalenza è una relazione di equivalenza e che somme dirette finite o infinite di elementi di una data classe di quasi equivalenza sono ancora rappresentazioni fattori nella stessa classe di quasi equivalenza. Le classi di equivalenza all'interno di una data classe di quasi equivalenza formano così un insieme ordinato nel quale esiste un'addizione associativa. Chiaramente, questo ‛semigruppo ordinato' è isomorfo agli interi positivi e oo quando la rappresentazione fattore è di tipo I. Vale anche l'inverso di questo enunciato e si hanno esattamente due possibilità. Il semigruppo ordinato può essere quello di tutti i numeri reali positivi e oo oppure può contenere un solo elemento. Conseguentemente, si dice che la rappresentazione fattore è di tipo II o di tipo III. Se ℋ1 è un sottospazio chiuso invariante della rappresentazione fattore V e Pℋ1 è il ‛proiettore' che applica ciascun vettore in ℋ(V) nella sua componente in ℋ1, Pℋ1 è un idempotente autoaggiunto nell'algebra commutante di V; inversamente ogni idempotente autoaggiunto o ‛proiettore' in R(V, V) definisce una sottorappresentazione di V. Queste rappresentazioni sono rappresentazioni fattori quasi equivalenti a V e la corrispondenza fra le classi di equivalenza di elementi di questa classe di quasi equivalenza e un sottosemigruppo di (0, ∞) determina una funzione dai proiettori in R(V, V) a (0, ∞). Questa funzione non è altro che la ‛funzione dimensione relativa' introdotta da von Neumann e Murray e da essi utilizzata per classificare i fattori nei tipi I, II e III. Per i tipi I e II l'applicazione identica può avere dimensione relativa finita o infinita; per il tipo I esiste una dimensione relativa minima che è un sottomultiplo positivo della dimensione dell'identità quando questa sia finita. Vi è così una sottoclassificazione nei tipi I1, I2, ..., I∞, II1, II∞ e III.
Per i gruppi che non sono di tipo I la conoscenza delle rappresentazioni unitarie irriducibili non è sufficiente per conoscere tutte le altre. È necessario conoscere anche le classi di equivalenza delle rappresentazioni fattori di tipo II e III. Questo risulta essere un problema assai più difficile e non esiste alcun esempio di un gruppo non di tipo I, le cui classi di quasi equivalenza delle rappresentazioni fattori siano state determinate.
Il problema di determinare le classi di equivalenza delle rappresentazioni unitarie irriducibili di un gruppo localmente compatto e separabile G, il quale, pur essendo di tipo I, non è né compatto né commutativo, può essere affrontato con metodi molto simili a quelli usati per il caso finito. Anche qui, come nel caso finito, un ruolo centrale viene assunto da una costruzione, detta di ‛induzione', la quale assegna una rappresentazione unitaria UL a ogni rappresentazione unitaria L di ciascun sottogruppo chiuso H di G. Quando lo spazio quoziente G/H ammette una misura invariante μ la definizione di UL è una generalizzazione diretta di quella data per i gruppi finiti. Si ottiene uno spazio di Hilbert restringendo le funzioni che soddisfano l'identità f(ξx) = Lξ f(x) alle funzioni di Borel per le quali x ???14??? (f(x)•f(x)) è μ sommabile quando la si consideri come una funzione sullo spazio quoziente G/H. Quando non esiste una misura invariante μ sullo spazio G/H, la definizione è un po' più complicata, ma non presenta serie difficoltà. Utilizzando la nozione di induzione così definita si può stabilire una generalizzazione piuttosto completa del teorema sui prodotti semidiretti di gruppi finiti enunciato nel cap. 7. Se G è prodotto semidiretto di un sottogruppo N chiuso normale separabile localmente compatto commutativo e di un altro sottogruppo chiuso H, il problema di trovare le rappresentazioni unitarie irriducibili di G può essere ricondotto a quello di trovare le rappresentazioni unitarie irriducibili di H e di certi suoi sottogruppi chiusi, esattamente nel modo in cui questa ricerca viene fatta nel caso finito.
Vi è tuttavia una restrizione. Le orbite dell'azione di H su Í devono essere di tipo tale che esista un sottoinsieme di Borel avente uno e un sol punto in comune con ciascuna di esse. Quando questa condizione non sussiste, si presentano molte rappresentazioni unitarie irriducibili in aggiunta a quelle descritte nel cap. 7 e per di più rappresentazioni fattori che non sono di tipo I. Quando la condizione restrittiva è soddisfatta, si può dimostrare che G è un gruppo di tipo I se, e soltanto se, tutti i sottogruppi di H che appaiono nella costruzione sono di tipo I. Come nel caso finito, vi è una generalizzazione nella quale compaiono rappresentazioni proiettive nelle quali N può essere non commutativo e l'estensione non deve necessariamente spezzarsi. Tuttavia, allo stato attuale delle cose, si deve supporre che N sia di tipo I. Inoltre si deve disporre di qualcosa che sostituisca, nell'ambito delle rappresentazioni, il procedimento di costruire il carattere χ1 × χ2 di un gruppo prodotto a partire dai caratteri χ1 e χ2 dei suoi fattori. Questo qualcosa può trovarsi nel concetto di ‛prodotto tensoriale' di due rappresentazioni, procedimento che ora descriveremo in quanto sostiene un ruolo importante in alcune applicazioni, soprattutto in fisica. A ogni coppia ℋ1 e ℋ2 di spazi di Hilbert separabili, è canonicamente associato un terzo spazio di Hilbert ℋ1 ⊗ ℋ2, chiamato il loro ‛prodotto tensoriale', e un'applicazione f, g ???14??? f ⊗ g di ℋ1 × ℋ2 (prodotto cartesiano) in ℋ1 ⊗ ℋ2. Questi oggetti sono dotati delle seguenti proprietà che li determinano univocamente. (1) f ???14??? f ⊗ g e g ???14??? f ⊗ g sono continue e lineari per ogni g e f fissati; (2) se ϕ1, ϕ2, ... e ψ1, ψ2, ... sono basi ortonormali in ℋ1 e ℋ2 rispettivamente, l'insieme di tutti i ϕi × ψj è una base ortonormale per ℋ1 ⊗ ℋ2. Per dare un esempio chiarificatore, è facile dimostrare che
ℒ2(S1, μ1) ⊗ ℒ2(S2, μ2)
può essere identificato canonicamente con
ℒ2(S1 × S2, μ1 × μ2),
in modo che f × g sia la funzione s1, s2 ???14??? (f1(s1), g2(s2)). Se T1 e T2 sono operatori lineari rispettivamente in ℋ1 e ℋ2, T1 ⊗ T2 è per definizione l'operatore lineare, definito univocamente, tale che (T1 ⊗ T2)(f × g) = T1(f) × T2(g). Se L e M sono rappresentazioni unitarie rispettivamente di G1 e G2 definiremo L × M, prodotto tensoriale di L e M, come la rappresentazione unitaria x, y ???14??? Lx ⊗ My. Si può dimostrare che L × M è irriducibile ogniqualvolta tanto L che M sono irriducibili e, se G1 o G2 è di tipo I, si può dimostrare che ogni rappresentazione unitaria irriducibile di G1 × G2 è del tipo L × M. Quando L e M hanno dimensione finita, si verifica immediatamente che
χL×M(x, y) = χL(x)χM(y),
cosicché
χL × χM = xL×M.
La teoria che lega le rappresentazioni unitarie di G a quelle di N e dei sottogruppi di G/N può essere usata induttivamente per studiare le rappresentazioni unitarie irriducibili di gruppi risolubili. Una serie di ricerche compiute fra il 1960 e il 1970 da alcuni matematici, e in modo particolare da Kirillov, Konstant, Auslander e Pukanszky, ha condotto a una teoria dei gruppi di Lie risolubili di tipo I che è veramente completa ed elegante.
La dimostrazione del teorema del prodotto semidiretto e le sue generalizzazioni possono essere sistemate in modo tale da farle apparire come corollari di un teorema di più ampia portata, detto ‛teorema di imprimitività'. Questo teorema è più o meno banale per i gruppi finiti, ma la sua dimostrazione nel caso generale contiene gran parte delle difficoltà tecniche che si trovano nella generalizzazione del teorema del prodotto semidiretto al caso localmente compatto separabile. Esso può essere considerato come una caratterizzazione delle rappresentazioni indotte. Per formularlo avremo bisogno di alcuni preliminari. Sia UL la rappresentazione unitaria del gruppo G, localmente compatto e separabile, indotta dalla rappresentazione unitaria L del sottogruppo chiuso H di G. Per ogni sottoinsieme di Borel E dello spazio quoziente G/H, sia E′ l'insieme di tutti gli x in G tali che Hx stia in E e sia PLE l'operatore lineare in H(UL) che manda f in ϕE, f, ove ϕE′ (x) = 1 se x sta in E′ e ϕE′ (x) = 0 se x non sta in E′. Si verifica che PLE è un operatore di proiezione e che l'applicazione E ???14??? PLE è una ‛misura a valori proiettori', nel senso che: a) PL0 = 0 e PLG/H è l'operatore identità; b) PLE1⋂E2 = PLE1 PLE2 = PLE2 PLE1 per tutti gli insiemi di Borel E1 e E2 in G/H; c) PLE1⋃E2⋃...⋃En⋃... = PLE1 + PLE2 + ... + PLEn + ... ogniqualvolta E1, E2, ..., En, è una successione di sottoinsiemi di Borel di G/H disgiunti due a due.
Un calcolo immediato mostra che le applicazioni x ???14??? ULχ e E ???14??? PLE soddisfano la seguente semplice ‛relazione di commutazione
ULxPLE = P[LE]x-1ULx o, equivalentemente,
ULxPLEULx-1 = P[LE]x-1 per tutti gli xe tutti gli E.
Sia ora V una rappresentazione unitaria arbitraria di G e sia E ???14??? PE una arbitraria misura a valori proiettori definita sullo spazio quoziente G/H, essendo H un sottogruppo chiuso di G. Sia P un ‛sistema di imprimitività' per V nel senso che PE opera in ℋ(V) e che VxPEVx-1 = P[E]x-1 per tutti gli x e tutti gli E. Il teorema di imprimitività afferma che esiste una rappresentazione unitaria L di H e un'applicazione unitaria W di ℋ(V) su H(UL) tale che WVxW-1 = ULx e WPEW1 = PLE per tutti gli x e tutti gli E. Inoltre L è univocamente determinata a meno di un'equivalenza e l'algebra commutante di L è isomorfa all'intersezione delle algebre commutanti di P e di V. Come spiegheremo con maggiori dettagli nel cap. 10, la relazione di commutazione soddisfatta da P e da V si può considerare come una generalizzazione delle relazioni di commutazione di Heisenberg nella meccanica quantistica e il teorema di imprimitività implica il teorema di Stone-von Neumann sull'unicità delle soluzioni irriducibili di tali relazioni di commutazione.
Proprio come nel caso finito, il procedimento induttivo non si può applicare quando s'incontrano gruppi semplici, ed esistono assai pochi esempi di gruppi semplici non compatti le cui rappresentazioni unitarie irriducibili siano ‛tutte' note. Bisogna accontentarsi del più modesto proposito di trovare un numero sufficiente di rappresentazioni irriducibili in modo da decomporre la rappresentazione regolare e trovare la ‛misura di Plancherel' associata. Per i gruppi non compatti, la determinazione di tante rappresentazioni irriducibili da poter decomporre la rappresentazione regolare non è assolutamente equivalente alla determinazione di ‛tutte' le rappresentazioni unitarie irriducibili. Sarà opportuno associare a una spiegazione del significato della ‛misura di Plancherel' un esame del modo in cui si estende la nozione di ‛carattere' alle rappresentazioni unitarie di dimensione infinita. Sia ϑ1, ϑ2, ..., ϑn, ... una base ortonormale nello spazio separabile di Hilbert ℋ. Diremo che la trasformazione lineare limitata T è un ‛operatore traccia' con Traccia (T) = Tr(T) = Σj (T(ϑj)•ϑj) se la serie al secondo membro converge assolutamente. Si vede facilmente che questa definizione è indipendente dalla scelta dei ϑj e che Tr(TA) esiste ed è uguale a Tr(AT) quando T è un operatore traccia e A è limitato. Sia ora G un gruppo localmente compatto separabile unimodulare con misura di Haar μ e sia V una rappresentazione unitaria di G. Per ogni funzione μ-sommabile a valori complessi su V esiste un unico operatore lineare limitato Vf in ℋ(V) tale che (Vf(ϑ)•ϑ′) = ∫ f(x)(Vx(ϑ)•ϑ′) dμ(x) per tutti i ϑ e ϑ′ in ℋ(V). L'insieme di tutte le f μ-sommabili per le quali Vf esiste è un sottospazio lineare ℳV dello spazio ℒ1(G, μ) delle funzioni sommabili e f ???14??? Tr(Vf) = ϑV (f) è un funzionale lineare su ℳV. Può accadere che ℳV sia denso in ℒ1(G, μ) e che esista una funzione a valori complessi χV su G tale che ∫ χV(x) f(x) dμ(x) = ϑV(f). Se V è di dimensione finita, ℳV = ℒ1(G, μ) e χV coincide con la Tr(Vx). Inoltre, ogniqualvolta ℳV è denso, ϑVdetermina χV a eccezione che su un insieme di μ-misura nulla. Pertanto è naturale chiamare ϑV il ‛carattere' di V quando ℳV sia denso e dire che il carattere di V è la funzione χV tutte le volte chee χV esiste. Supponiamo ora che G sia di tipo I e sia ν una qualsiasi misura su Ø σ-finita, nel senso che Ø sia un'unione numerabile di insiemi di misura finita e tale che, per qualche sottoinsieme di Borel N di G con ν(N) = 0, esista un sottospazio ℳN dello spazio delle funzioni continue su G il quale sia denso in ℒ1(G, μ) contenuto in ℳL per tutte le L in Ø - N e tale che L ???14??? χL(f) sia ν-sommabile per tutte le f in ℳN. In questa ipotesi f ???14??? ∫ χL(f) dν(L) è un funzionale lineare su ℳN. Si può dimostrare che ν può essere scelta in guisa che ∫ χL(f) dν(L) = f(e) per tutte le f in un opportuno ℳN e che ν è univocamente determinato da questa proprietà e dalla scelta di μ. Questa misura ???42???, definita a meno di una costante moltiplicativa, si chiama la ‛misura di Plancherel' per G e la formula
viene detta ‛formula di Plancherel'. Per descrivere ???42??? in termini concreti, basta ovviamente conoscere un sottoinsieme Ø1 di Ø tale che ???42???(Ø = Ø1) = 0; tali insiemi sono più facili da descrivere che lo stesso Ø.
Uno degli scopi principali di una lunga serie di lavori di I. M. Gelfand, Naimark e Graev, da una parte, e di Harish-Chandra, dall'altra, è stato quello di determinare Ø1 e ???42??? per i gruppi di Lie semisemplici. Sia G un gruppo di Lie semi-semplice connesso con centro finito e siano A e K i sottogruppi chiusi che compaiono nella decomposizione di Iwasawa (si veda la fine del cap. 6). Sia M il sottogruppo di tutti gli elementi k di K che commutano con tutti gli elementi di A. L'insieme NAM di tutti gli elementi della forma nam con n in N, a in A e m in M è il sottogruppo chiuso di G che è il prodotto semidiretto di N e AM. Se χ è un qualunque carattere a una dimensione di A e L è una qualunque rappresentazione unitaria irriducibile di M, la funzione nam ???14??? χ(a)Lm definisce una rappresentazione unitaria χL di NAM e la rappresentazione indotta UχL risulta essere irriducibile per tutti gli L e tutti i χ, a eccezione di un sottoinsieme di  di misura di Haar nulla. Quando G è un gruppo di Lie complesso, le rappresentazioni irriducibili UχL possono essere prese come Ø1 e in tal caso la formula di Plancherel si può ottenere in modo particolarmente semplice. Un libro pubblicato nel 1950 da Gelfand e Naimark contiene una dimostrazione per SL(n, C) e per gli altri gruppi complessi classici; il caso generale complesso semisemplice venne affrontato nel 1954 da Harish-Chandra. L'esempio di dimensione minima di un gruppo di Lie semisemplice non complesso e non compatto è fornito da SL(2, R) e fu studiato dettagliatamente da V. Bargmann in un classico lavoro pubblicato nel 1947. In questo caso alle rappresentazioni unitarie irriducibili UχL descritte dianzi deve accompagnarsi una famiglia numerabile di rappresentazioni unitarie irriducibili ciascuna delle quali ha misura di Plancherel positiva e si presenta come una sottorappresentazione irriducibile della rappresentazione regolare. Questa famiglia si chiama ‛serie discreta'. Nel caso generale, la serie discreta può esistere oppure no (vale a dire che la rappresentazione regolare può ammettere o non ammettere sottorappresentazioni irriducibili) e vi saranno anche altre famiglie che saranno anch'esse esaminate. Tuttavia, nella fase iniziale di questa ricerca, Harish-Chandra riuscì a dimostrare che, nel problema generale, il punto cruciale consiste nel trovare la serie discreta quando essa esista. Intorno al 1950 molti esempi vennero studiati da Gelfand e Graev e una soluzione generale venne annunciata da Harish-Chandra nel 1963 ed esposta in una serie di lavori successivi. Harish-Chandra trovò i caratteri degli elementi della serie discreta piuttosto che le rappresentazioni stesse, ma successivi lavori di molti altri matematici completarono questo punto. Fra l'altro, Harish-Chandra riuscì a dimostrare che, per rappresentazioni unitarie di gruppi di Lie semisemplici, il carattere non soltanto esiste, ma è definito da una funzione analitica su un insieme aperto denso.
Sia μ una misura di Haar invariante a destra nel gruppo compatto G localmente separabile e sia ℒ1(G, μ) lo spazio di tutte le funzioni a valori complessi sommabili su G. Se f e g sono elementi di ℒ1(G, μ), ∫ f(xy-1)g(y) dμ(y) esiste per quasi tutti gli x e definisce una funzione f * g in ℒ1(G, μ) che viene chiamata la ‛convoluzione' di f e g. Rispetto a questa moltiplicazione, ℒ1(G, μ) non soltanto è uno spazio di Banach (con norma ∥ f ∥ = ∫ ∣ f(x) ∣ dμ(x)), ma è anche un'algebra lineare associativa in cui la norma del prodotto soddisfa alla condizione ∥ f * g ∥ ≤ ∥ f ∥ ∥ g ∥. Come tale essa è un esempio di ‛algebra di Banach'. Quando G è finito, tale algebra si riduce all'algebra di gruppo, che abbiamo definito in precedenza, e costituisce una possibile generalizzazione di quest'ultima.
9. Gruppi algebrici.
Dato un corpo algebricamente chiuso ℱ e un intero positivo n, consideriamo il gruppo GL(n, ℱ) di tutte le matrici invertibili n × n con elementi in ℱ. Se fij(A) indica l'elemento di ℱche appare nella i-esima riga e nella j-esima colonna di A, l'applicazione A ???14??? ϕ(A) = det A-1, f11(A), f12(A), ..., f1n(A), f21(A), ..., fnn(A) è un'applicazione biunivoca di GL(n, ℱ) in un sottoinsieme dello spazio di tutte le n2 + 1-uple di ℱ. Quando n = 2, questo sottoinsieme consiste delle quintuple a0, a11, a12, a21, a22 tali che a0(a11a22 − a12a21) − 1 = 0 e come tale è una ‛varietà algebrica affine'. Per n > 2 vale un risultato analogo, ma i polinomi sono più complicati. Più in generale, una varietà algebrica affine su ℱ viene definita assegnando un intero positivo m e un numero finito P1, ..., Pk di polinomi in m variabili con coefficienti in ℱ. La varietà consta dell'insieme di tutte le m-uple di elementi di ℱ per le quali si annullano i polinomi P1, ..., Pk. Naturalmente la stessa varietà può essere definita da molti diversi insiemi di polinomi. Ogni polinomio in m variabili definisce una funzione sull'insieme delle m-uple a valori in ℱ e quindi per restrizione una funzione sulla varietà a valori in ℱ. Queste funzioni, definite sulla varietà e a valori in ℱ si chiamano ‛funzioni regolari'. Esse formano un'algebra commutativa su ℱ a generazione finita. Due varietà algebriche affini (eventualmente corrispondenti a diversi valori di m) si dicono ‛isomorfe come varietà affini' se esiste un'applicazione biunivoca ϕ dai punti dell'una ai punti dell'altra, tale che le funzioni regolari sulla prima varietà siano esattamente le funzioni q ???14??? f(ϕ(q)), dove f varia fra funzioni regolari sulla seconda varietà. In altre parole, a prescindere da una particolare realizzazione concreta, una varietà affine su ℱ è descritta in modo completo quando si conoscano i suoi punti come elementi di un insieme astratto V e quando si indichi quali funzioni definite su V e a valori in ℱ siano le funzioni regolari. Di fatto è possibile dimostrare che ogni omomorfismo dell'algebra delle funzioni regolari in ℱ ha la forma f ???14??? f(v) per un opportuno punto v nella varietà; da ciò segue che è possibile ricostruire la varietà quando sia nota l'algebra delle funzioni regolari come un'algebra astratta su ℱ. Quest'algebra ha sempre generazione finita, contiene le costanti e non contiene nessun elemento f tale che si abbia fn = 0 per un intero n ad eccezione di f = 0. Inversamente si vede facilmente che ogni algebra su ℱ dotata di queste proprietà è l'algebra delle funzioni regolari su qualche varietà algebrica affine su ℱ.
Sia V una varietà algebrica affine su ℱ e sia A la sua algebra di funzioni regolari. Per ogni sottoinsieme V1 di V, sia V1⊥ l'insieme di tutte le f in A tali che f(v) = 0 per tutti i v in V1 e sia V- 1 l'insieme di tutti i v in V tali che f(v) = 0 per tutte le f in V1⊥. Quei sottoinsiemi V1 per i quali V- 1 = V1 si dicono i ‛chiusi di Zariski' e sono precisamente i sottoinsiemi chiusi per una certa topologia in V che si chiama topologia di Zariski. Ogni sottoinsieme chiuso secondo Zariski è una varietà algebrica affine le cui funzioni regolari sono le restrizioni delle funzioni regolari in V.
L'applicazione ϕ descritta all'inizio di questo paragrafo trasforma il gruppo GL(n, ℱ) in un ‛gruppo algebrico' definendo su di esso la struttura di una varietà algebrica affine. Più in generale, ogni sottogruppo di GL(n, ℱ) chiuso secondo Zariski possiede anch'esso una struttura (indicata dianzi) e, rispetto a essa, è un gruppo algebrico. In termini più astratti, un gruppo algebrico (lineare) su ℱ è per definizione un gruppo G che è anche una varietà algebrica su ℱ e nel quale le strutture di gruppo e di varietà sono legate fra loro in modo tale che x, y ???14??? f(xy-1) sia una funzione regolare su G × G qualunque sia la funzione regolare f su G. (Le funzioni regolari su G × G sono proprio le combinazioni lineari finite con coefficienti in ℱ delle funzioni x, y ???14??? g1(x)g2(y), ove g1 e g2 sono funzioni regolari su G). Si può dimostrare che ogni gruppo algebrico (lineare) in questo senso è isomorfo, come gruppo algebrico, a un sottoinsieme chiuso secondo Zariski di GL(n, ℱ) per un n opportuno; questo fatto permette di darne una definizione equivalente e più concreta. Poiché in questo paragrafo non parleremo di gruppi algebrici non lineari, il termine ‛lineare' verrà da ora in poi omesso. È importante tenere presente che rispetto alla topologia di Zariski, un gruppo algebrico non è un gruppo topologico nel senso del cap. 5.
Mentre le definizioni precedenti continuano ad avere significato quando ℱ sia sostituito da un corpo k non algebricamente chiuso, i gruppi corrispondenti non sono varietà algebriche affini. Per i geometri algebrici è importante includere in ogni varietà algebrica tutte le soluzioni delle equazioni che la definiscono e non soltanto quelle le cui coordinate appartengono al corpo che si sta considerando. Conseguentemente un gruppo algebrico su un corpo k non algebricamente chiuso è sempre definito in relazione a un corpo algebricamente chiuso ℱ il quale contiene k ed è il gruppo Gk = G ⋂ GL(n, k) di tutti i ‛punti razionali' su un sottogruppo G, chiuso secondo Zariski, di GL(n, ℱ). Il sottogruppo G, chiuso secondo Zariski, deve essere definito su k nel senso che i polinomi che lo determinano possano essere scelti in modo da avere tutti i coefficienti in k. Così ogni Gk può di fatto essere ottenuto mediante l'applicazione diretta della definizione data nel caso algebricamente chiuso e le ‛funzioni k-regolari' sono le funzioni definite su Gk e a valori in k che si otterrebbero applicando questa definizione. D'altra parte è sovente essenziale prendere in considerazione il gruppo più ampio G, che è una varietà algebrica, e del quale Gk è un sottogruppo. Per esempio, perché Gk e Gk′ siano isomorfi come gruppi su k, non è sempre sufficiente avere un isomorfismo ϕ fra Gk e Gk′ come gruppi astratti, tale che le funzioni k-regolari su Gk siano esattamente le funzioni x ???14??? f(ϕ(x)), ove f varia fra le funzioni k-regolari su Gk′. L'isomorfismo ϕ deve essere la restrizione a Gk di un isomorfismo di G e G′ come gruppi su ℱ. Questa ulteriore condizione vale automaticamente ogniqualvolta k sia infinito, poiché in tal caso si può dimostrare che G (rispettivamente G′) è la chiusura, per la topologia di Zariski, di Gk (rispettivamente Gk′).
Esistono tuttavia dei casi importanti in cui tale condizione deve essere posta separatamente. La definizione inoltre è ancora più complicata, a meno che k sia ‛perfetto' nel senso che abbia caratteristica zero oppure caratteristica p e contenga la radice p-esima di ciascuno dei suoi elementi.
Per definizione, una ‛derivazione' di un'algebra commutativa A su un corpo k è una trasformazione lineare D di A, considerata come spazio vettoriale, in se stessa, tale che D(fg) = fD(g) + D(f)g, per tutti gli f e i g in A.
Se D1 e D2 sono derivazioni, f ???14??? D1(D2(f)) − D2(D1(f)) è anch'essa una derivazione. Essa viene indicata con la notazione [D1, D2]. L'insieme di tutte le derivazioni di A è chiaramente uno spazio vettoriale su k e, con l'operazione D1, D2 ???14??? [D1, D2], esso diventa un'algebra di Lie su k. Sia ora A l'algebra di tutte le funzioni k-regolari sul gruppo algebrico Gk definito su k. Per ogni x in Gk sia Tx la trasformazione lineare che manda f in fx, ove fx(y) = f(yx). È possibile dimostrare che l'insieme di tutte le derivazioni D di A tali che TxD = DTx per tutti gli x in Gk è una sottoalgebra di Lie di ‛dimensione finita' dell'algebra di Lie di tutte le derivazioni su A. Essa viene chiamata l'‛algebra di Lie' del gruppo algebrico Gk. Quando ℱ è di caratteristica zero, esiste una teoria algebrica che collega i gruppi algebrici con le loro algebre di Lie, che è perfettamente simile a quella che vale per i gruppi di Lie.
La nozione di gruppo algebrico (sul corpo dei numeri complessi) venne introdotta verso la fine del XIX secolo da L. Maurer, ma, fino al 1951, anno in cui apparve il secondo volume del trattato di C. Chevalley, Théorie des groups de Lie, essa fu assai poco sviluppata. Questo libro, in cui Chevalley pone in modo sistematico i fondamenti della teoria, fu alla base di una serie di ricerche successive che si stanno ancora sviluppando. Il terzo volume di questo trattato, che apparve nel 1955, mostra dettagliatamente come sia possibile trasportare alle algebre di Lie dei gruppi algebrici su un corpo di caratteristica zero i teoremi classici di struttura per le algebre di Lie dei gruppi di Lie. Un importante passo avanti fu compiuto da A. Borel in un lavoro ormai classico pubblicato nel 1956. Verso la fine del XIX secolo, Picard e Vessiot applicarono le idee di Galois alle equazioni differenziali lineari e nel 1948 E. Kolchin sviluppò alcuni aspetti della teoria dei gruppi algebrici al fine di applicare a essi una versione riveduta della teoria di Picard-Vessiot. In particolare egli dimostrò certi teoremi di struttura direttamente, senza far ricorso ai teoremi di struttura per le algebre di Lie. Seguendo le orme di Kolchin, Borel dimostrò che anche molti dei teoremi di Chevalley si potevano ottenere mediante considerazioni dirette ‛globali' e potevano essere così estesi a gruppi algebrici su corpi modulari dove l'algebra di Lie non è legata al gruppo in modo soddisfacente.
Borel si occupò principalmente del caso di gruppi su un corpo ℱ algebricamente chiuso; uno dei suoi risultati più importanti afferma che in tal caso ogni elemento in un gruppo connesso sta in un sottogruppo risolubile chiuso connesso massimale, due sottogruppi siffatti essendo fra loro coniugati. Tali sottogruppi sono ora noti come ‛sottogruppi di Borel' e sostengono un ruolo importante sia nella teoria dei gruppi di Lie che in quella dei gruppi algebrici. Ogni sottogruppo contenente un sottogruppo di Borel è necessariamente chiuso e connesso e questi sottogruppi vengono chiamati sottogruppi ‛parabolici' di G. Ciascun sottogruppo di Borel è contenuto in un numero finito di sottogruppi parabolici e due di questi non sono mai tra loro coniugati. Ogni sottogruppo parabolico è l'intersezione dei sottogruppi massimali parabolici che lo contengono. Le dimensioni dei sottogruppi parabolici contenenti un sottogruppo di Borel fissato sostengono un ruolo centrale nell'analisi della struttura di quei gruppi algebrici connessi che sono ‛semisemplici', nel senso che non hanno sottogruppi connessi normali risolubili.
Si dice che un elemento x di GL(n, ℱ) è ‛unipotente' se, per qualche n, (x − 1)n = 0. Si può dimostrare che, se G1 e G2 sono sottogruppi chiusi nella topologia di Zariski di GL(n1, ℱ) e GL(n2, ℱ), ogni isomorfismo di G1 e G2 come gruppi algebrici trasforma elementi unipotenti in elementi unipotenti così che ha senso dire che un elemento di un gruppo algebrico G è unipotente. Se G′ è un gruppo algebrico connesso e risolubile, l'insieme U di tutti i suoi elementi unipotenti è un sottogruppo chiuso normale e connesso e G′ è un prodotto semidiretto di U e di un sottogruppo chiuso H, isomorfo al prodotto diretto di un numero finito di copie di GL(1, ℱ). Questo accade in particolare quando G′ = B è un sottogruppo di Borel di un gruppo algebrico semisemplice G e allora il gruppo N di tutti gli x in G tali che xHx-1 = H è un sottogruppo connesso per il quale B ⋂ N = H e W = N/H è un gruppo finito generato dai suoi elementi di ordine due. Nel 1962, allo scopo di estendere i risultati sui teoremi di struttura ai corpi algebrici Gk definiti su corpi non algebricamente chiusi, J. Tits assiomatizzò le proprietà dei gruppi B e N considerati dianzi e introdusse il fecondo concetto di ‛coppia B-N' o, come viene anche chiamato, ‛sistema di Tits'. Se G è un gruppo (astratto) arbitrario, la coppia B-N in G è per definizione - una coppia di sottogruppi B, N tali che: 1) B e N generino G; 2) W = N/H abbia un insieme R di generatori di ordine 2 tali che per ogni r in R e ogni w in W sia: a) rBr-1 ≠ B; b) per tutti i b1 e b2 in B, r1b1wb2 sia del tipo b3wb4 o b3rwb4 per b3 e b4 opportunamente scelti in B.
Si può dimostrare che le proprietà dei sottogruppi parabolici di un gruppo algebrico semisemplice sono una conseguenza di questi assiomi. Questo fatto e la nozione di coppia B-N hanno avuto un ruolo utilissimo in numerose ricerche.
La struttura dei gruppi algebrici Gk, dove G è un gruppo algebrico semisemplice (o, più in generale, un gruppo ‛riduttivo') su un corpo algebricamente chiuso, ha fatto ormai notevoli progressi per merito essenzialmente, ma non esclusivamente, di Borel e di Tits. Per mezzo dei corpi Gk, ove k è un corpo finito, essa si collega con la teoria dei gruppi semplici finiti.
10. Estensioni di gruppi e coomologia di un gruppo.
Siano N e Q due gruppi e sia G l'insieme di tutte le coppie n, q con n in N e q in Q. Sia αq un automorfismo di N definito per ciascun q in Q e sia η una funzione definita su Q × Q e a valori in N. Definiamo un ‛prodotto' per elementi di G ponendo
(n1, q1)(n2, q2 = (n1αq1(n2)η(q1, q2), q1,q2).
Un calcolo diretto mostra che G è un gruppo rispetto a questo ‛prodotto' con identità (e, e) se, e soltanto se, sono soddisfatte le identità seguenti:
η(e, q) ≡ η(q, e) ≡ e, (1)
η(q1, q2)η(q1, q2, q3) ≡ αq1(η(q2, q3))η(q1, q2, q3) (2)
αq1q2(n) ≡ η-1(q1, q2)αq1(αq2(n))η(q1, q2). (3)
Se esse sono soddisfatte, n ???14??? (n, e) un isomorfismo di N con un sottogruppo normale di G e (n, q) ???14??? q è un omomorfismo di G su Q, il cui nucleo è il sottogruppo normale N′ costituito da tutti gli (n, e). In altre parole, G è un'estensione di Q mediante N. Inversamente, ogni estensione di Q mediante N nasce in questo modo da un'opportuna scelta di η e dell'applicazione q ???14??? αq. Nel caso particolare di un'estensione spezzata, η può essere scelta in modo che η(q1, q2) = e per tutti i q1 e q2 e in tal caso la (3) si riduce al fatto che q ???14??? αq è un omomorfismo. In ogni caso, l'insieme Q′ degli elementi del tipo e, q incontra ogni classe laterale di N′ in uno e un sol punto e risulta (e, q1)•(e, q2) = (η(q1, q2), q1q2), così che η ‛indica' in quale misura l'insieme Q′ delle classi laterali non è un gruppo.
Date una η e un'applicazione q ???14??? αq soddisfacenti (1) (2) e (3), sia q ???14??? b(q) una funzione arbitraria da Q a N tale che b(e) = e. Posto
η′(q1, q2) = b(q1)αq1(b(q2))η(q1, q2))b(q1, q2)-1, (4)
αq′ (η) = b(q)αq(η)b(q)-1, (5)
un semplice calcolo mostra che anche η′ e α′ soddisfano (1) (2) e (3) e che la struttura di gruppo definita in G partendo da η′ e α′ è isomorfa a quella definita a partire da η e α, mediante l'isomorfismo n, q ???14??? nb(q), q. Estendendo una nomenclatura che introdurremo più avanti, diremo che η, α e η′, α′, soddisfacenti (1) (2) e (3) sono ‛coomologhi' se esiste un b per il quale valgono le (4) e (5). Si vede facilmente che questa nozione ripartisce la classe di tutte le coppie η, α soddisfacenti le (1), (2) e (3) in classi disgiunte di elementi fra loro coomologhi e che, a meno di un'identificazione banale, il problema di trovare tutte le estensioni di Q mediante N è equivalente a trovare queste ‛classi di coomologia'.
Questo problema può essere formulato in modo più elegante, e diviene più facile, nel caso particolare in cui N è commutativo. In tal caso la (3) si riduce alla αq1q2(n) ≡ αq1(αq2(n)) ed è indipendente da η. Inoltre, η, α e η′, α′ sono coomologhi se, e soltanto se, α = α′ e
η′(q1, q2) = η(q1, q2)b(q1)αq1(b(q2))b(q1q2)-1. (6)
Pertanto tutti gli α′ possibili possono essere trattati uno alla volta e, per ogni scelta di α soddisfacente la (3), il problema si riduce a trovare tutte le funzioni η che soddisfano la (1) e la (2), due funzioni siffatte essendo identificate quando soddisfano la (6). Quando N è commutativo, tuttavia, le funzioni soddisfacenti la (1) e la (2) per un α fissato formano un gruppo commutativo Z rispetto alla moltiplicazione puntuale e quelle coomologhe alla scelta banale di η formano un sottogruppo B. Chiaramente la (6) è equivalente a dire che η e η′ si trovano nella stessa classe laterale B di Z. Quindi le classi di coomologia formano un gruppo - il gruppo quoziente Z/B - e il problema dell'estensione, per N, Q e α dati, diviene quello di determinare tale gruppo quoziente.
In generale, un ‛Q-modulo' su un dato gruppo Q è per definizione un gruppo commutativo N con un omomorfismo q ???14??? αq di Q nel gruppo di tutti gli omomorfismi di N. La definizione di C/B, data precedentemente, si applica evidentemente a ogni Q-modulo N, α e inoltre si può generalizzare nel modo seguente. Per ogni k = 1, 2, ..., sia Ck(Q, N, α) il gruppo, rispetto alla moltiplicazione puntuale, delle funzioni η dalle k-uple di elementi di Q a N, tali che η(q1, q2, ..., qk) = e se qj = e per qualche j. Per ogni η in Ck(Q, N, α) sia δη l'elemento di Ck+1(Q, N, α) tale che
δη(q1, q2, ..., qk+1) = αq1(η(q2, q3, ..., qk+1) •
• (η(q1q2, q3, ..., qk+1))-1(η(q1, q2q3, q4, ..., qk+1) •
• ... • η(q1, q2, ..., qkqk+1)j • η(q1, q2, ..., qk)j′,
ove j e j′ sono rispettivamente uguali a 1 e −1 oppure −1 e 1 secondo che k sia pari o dispari. Pertanto η ???14??? dg è un omomorfismo di Ck(Q, N, α) su Ck+1(Q, N, α) e si verifica facilmente che δδη è l'identità, così che il sottogruppo Bk(Q, N, α) di tutti gli elementi di Ck(Q, N, α) del tipo δb per un opportuno b in Ck+1(Q, N, α) è contenuto nel sottogruppo Zk(Q, N, α) di tutti gli η in Ck(Q, N, α) per i quali δη è l'identità. Due elementi di Zk(Q, N, α) si dicono coomologhi se l'uno può essere ottenuto dall'altro moltiplicando quest'ultimo per un elemento di Bk(Q, N, α) e il gruppo quoziente Æk(Q, N, α) = Zk(Q, N, α)/Bk(Q, N, α) si chiama il k-esimo gruppo di coomologia di Q con coefficienti nel Q modulo N, α. Quando k = 2, i gruppi Zk(Q, N, α) e Bk(Q, N, α) si riducono ai gruppi Z e B precedentemente introdotti in relazione al problema delle estensioni dei gruppi.
Il gruppo Z′(Q, N, α) è il gruppo di tutte le funzioni η da Q a N tali che η(q1q2) = αq1(η(q1))η(q2). Tali funzioni appaiono in molti problemi della teoria dei gruppi e sono note con il nome di omomorfismi incrociati. Essi si riducono chiaramente a omomorfismi ordinari quando αq(n) ≡ n. Pertanto Æ1(Q, N, α) è il gruppo quoziente del gruppo di tutti gli omomorfismi incrociati modulo il sottogruppo degli ‛omomorfismi principali incrociati'; il gruppo cioè di tutti quelli del tipo q ???14??? αq(n0)n0-1. Naturalmente ogni gruppo commutativo N diventa un Q-modulo per ogni gruppo commutativo Q se si assume come αq l'automorfismo identico. Se N è il gruppo dei numeri complessi di modulo uno e α è la ‛scelta dell'identità', Z2(Q, N, α) è precisamente il gruppo dei moltiplicatori σ per le rappresentazioni dei gruppi finiti discusse nel cap. 7. Inoltre, B2(Q, N, α) diventa il sottogruppo dei moltiplicatori banali. Così Æ2(Q, N, α) è in questo caso il gruppo dei moltiplicatori proiettivi ‛essenzialmente distinti'.
I successivi gruppi di coomologia Æk(Q, N, α), con k > 2, vennero introdotti dapprima in relazione a una notevole analogia con la topologia. Sia M una varietà il cui rivestimento semplicemente connesso ???39??? sia ‛contraibile', sia cioè ‛deformabile con continuità in un punto'. Il gruppo fondamentale G di M determina allora tutti i gruppi di omologia e di coomologia di M e i gruppi di coomologia con coefficienti in N sono isomorfi ai gruppi Æk(Q, N, α) definiti precedentemente, dove αq è l'identità per ogni q. La scoperta di questa relazione con la topologia e la definizione di Æk(Q, N, α) per k > 2 si deve a Eilenberg e Mac Lane che per primi la pubblicarono nel 1943. A essa erano indipendentemente giunti Eckmann e Freudenthal, che pubblicarono i loro risultati due o tre anni più tardi. Il termine ‛gruppo di coomologia' proviene dalla topologia. Con terminologia propria della topologia, gli elementi di Zk(Q, N, α) e Bk(Q, N, α) si chiamano rispettivamente ‛k-cocicli' e ‛k-cobordi'.
Mentre per k > 2 gli analoghi dei gruppi di coomologia non hanno applicazioni così immediate nella teoria dei gruppi come Æ1(Q, N, α) e Æ2(Q, N, α), la loro teoria è interessante in se stessa e si rivela inoltre utile nel calcolare effettivamente la struttura, per scelte particolari di Q, N e α, di Æ1(Q, N, α) e Æ2(Q, N, α).
Lo sviluppo della teoria coomologica dei gruppi ricevette un considerevole impulso intorno al 1950, quando Nakayama, Hochschild, Artin e Tate scoprirono che essa ha importanti applicazioni a quella parte della teoria dei numeri che si chiama ‛teoria del corpo di classi' (v. cap. 13). Di fatto, i teoremi principali di quest'ultima teoria possono essere riformulati con il linguaggio della coomologia dei gruppi e questa nuova formulazione si rivela assai utile.
Nella teona astratta, uno dei problemi più importanti è naturalmente quello di calcolare il gruppo di coomologia Hk(Q, N, α) quando siano dati Q, N, e α. Il caso più semplice è quello in cui Q è un gruppo ciclico di ordine m; in tal caso si ottiene una soluzione completa nel modo seguente. Sia N0 il sottogruppo di tutti gli n tali che αq(n) = n per tutti i q, sia N00 il sottogruppo di tutti gli elementi di N del tipo Πq∈Q αq(n) per n ∈ N. È chiaro allora che N00 ⊆ N0 e si può dimostrare che Hk(Q, N, α) è isomorfo al gruppo quoziente N0/N00 per k = 2, 4, 6, 8, ... . Similmente Hk(Q, N, α), per k = 1, 3, ..., è isomorfo al gruppo quoziente N1/N2, ove N1 è il sottogruppo di tutti gli n tali che Πq∈Q αq(n) = e, e N2 ⊆ N1 è il gruppo di tutti gli m ∈ N del tipo αq0(n)n-1, ove q0 è un generatore fissato di Q. Quando Q è un gruppo ciclico infinito, si può dimostrare che Hk(Q, N, α) si riduce all'identità per k ≥ 2 e che H1(Q, N, α) è isomorfo a N.
Se Q1 è un sottogruppo di Q, ogni Q-modulo N, α è ovviamente anche un Q1-modulo in modo naturale e ogni k-cociclo a valori in N resta un k-cociclo se considerato come una funzione di k variabili in N1. Poiché inoltre cobordi si restringono a cobordi, esiste un ‛omomorfismo naturale' di Hk(Q, N, α) in Hk(Q1, N, α).
Quando Q è finito e Qp1, ..., Qpr sono i suoi p-sottogruppi di Silow, gli omomorfismi naturali di Hk(Q, N, α) nei vari Hk(Qpj, N, α) definiscono un omomorfismo di Hk(Q, N, α) nel prodotto diretto, rispetto a j, degli Hk(Qpj, N, α) e questo omomorfismo risulta essere un isomorfismo. Poiché Hk(Q′, N, α) è un p-gruppo ogniqualvolta Q′ è un p-gruppo, ne segue che la ‛p-componente' di Hk(Q, N, α), costituita da tutti gli elementi i cui ordini sono potenze di p, è banale ogniqualvolta Hk(Qp, N, α) è banale.
Se K è un sottogruppo normale del gruppo Q, ogni Q/K-modulo N, α è anche un G-modulo; il sottogruppo Nk di N costituito da tutti gli n tali che αq(n) = n per tutti i q ∈ K è anch'esso un G-modulo. Inoltre, l'applicazione naturale di Zk(Q/K, N, α in Zk(Q, N, α) definisce un omomorfismo ψk di Hk(Q/K, Νk, α) in Hk(Q, M, α). ψk si chiama ‛omomorfismo d'inflazione' e l'omomorfismo ϕk di Hk(Q, N, α) in Hk(K, N, α) definito dianzi (con una diversa notazione) si chiama ‛omomorfismo di restrizione'. Si può dimostrare che η ???14??? ϕk(ψk(η)) applica ogni η all'identità, cosicché il ‛rango' AkQ di ψk è contenuto nel nucleo BkQ di ϕk. Nel caso particolare in cui k = 1, si può dimostrare che la successione di omomorfismi
è esatta, nel senso che il rango di ciascun omomorfismo è precisamente il nucleo di quello che lo segue. Questo vale anche per valori superiori di k ogniqualvolta Hj(K, N, α) = {e} per 1 ≤ j ≤ k − 1. Questo significa non solo che AkQ = BkQ, ma anche che ψk è biunivoco. Quindi Hk(Q, N, α) ha un sottogruppo isomorfo a Hk(Q/K, Nk, α), il cui quoziente è isomorfo a un sottogruppo di Hk(K, N, α). La conoscenza di Hk(Q/K, Nk, α) e di Hk(K, N, α) fornisce qualche informazione circa Hk(Q, N, α). Quando k > 1 e Hj(K, N, α) ≠ {e} per 1 ≤ j ≤ k − 1 la situazione diviene più complicata in quanto i diversi valori di k non possono essere considerati separatamente. Tuttavia, mediante una tecnica algebrica nota sotto il nome di ‛successione spettrale' si possono ottenere interessanti osservazioni su Hk(Q, N, α) quando si conoscano gli Hk′ (Q/K, Nk, α) e gli Hk′ (K, N, α) per tutti i k′. Le successioni spettrali vennero introdotte in topologia da J. Leray nel 1945 in connessione con i gruppi di coomologia degli ‛spazi fibrati'. Esse vennero adattate allo studio della coomologia dei gruppi da Hochschild e Serre. Alcune delle idee fondamentali erano state messe a fuoco da Lyndon in ricerche indipendenti da quelle condotte da Leray.
I teoremi che sono stati esposti precedentemente sono soltanto frammenti di una teoria che non possiamo qui esporre con maggiori dettagli per ragioni di spazio.
Mentre all'inizio ci si occupava soltanto dei gruppi finiti o dei gruppi finiti discreti, un progresso considerevole è stato ormai compiuto anche per i gruppi topologici. La prima esposizione sistematica sufficientemente ampia è stata pubblicata nel 1964 da C. C. Moore.
Proprio come per la teoria delle rappresentazioni, una notevole parte della teoria della coomologia dei gruppi può essere dedotta da una teoria coomologica più generale di gruppi e algebre associative. I fondamenti di quest'ultima vennero posti da Hochschild nel 1945 in ricerche più o me no indipendenti da quelle di Eilenberg e MacLane. Esiste inoltre una teoria coomologica significativa delle algebre di Lie.
11. Gruppi non discreti di trasformazioni: sistemi dinamici e teoria ergodica.
Sia G un gruppo e sia S un ‛G-spazio', nel senso che a ogni s in S e a ogni x in G è associato un elemento [s]x in G, in modo che siano soddisfatte le due condizioni seguenti:
[s]e = s (7)
[[s]x]y = [s]xy, (8)
per ogni s in S e tutti gli x, y in G. In altre parole, dato un omomorfismo di G nel gruppo delle trasformazioni biunivoche di S in se stesso, indichiamo con [s]x la trasformata di s per l'immagine omomorfa di x. Come abbiamo notato nei capp. 1 e 2, la nozione di gruppo è un'astrazione da quella di gruppo di trasformazioni e per ogni gruppo G esiste il problema di analizzare e classificare le sue possibili realizzazioni come gruppo di trasformazioni; in altre parole, classificare e analizzare i possibili G-spazi. Se {Sα} è una famiglia arbitraria di G-spazi per un dato gruppo G, si può definire un nuovo G-spazio S, che si chiama ‛somma diretta' di Sα, nel modo seguente. Indichiamo con S l'insieme di tutte le coppie α, s con s in Sα e prendiamo per definizione [α, s]x uguale a α, [s]x. Ricordiamo che S1 e S2 si dicono ‛isomorfi' (come G-spazi) se esiste un'applicazione biunivoca ϑ di S1 su S2 tale che ϑ([s]x) = [ϑ(s)]x per ogni s in S1 e ogni x in G. Ricordiamo inoltre che l'orbita Os di s in G è, per definizione, l'insieme di tutti gli [s]x per un s fissato e un x variabile in G. È chiaro che due orbite in un G-spazio S coincidono oppure sono disgiunte, che ogni orbita è essa stessa un G-spazio e che ogni G-spazio è equivalente alla somma diretta dei G-spazi definiti dalle sue orbite. Il problema di studiare il G-spazio più generale si riduce quindi immediatamente al problema di studiare il G-spazio più generale che è ‛transitivo', nel senso che esiste in esso una sola orbita o, equivalentemente, che non è equivalente alla somma diretta di due G-spazi non vuoti. Come abbiamo detto nel cap. 2, il problema di trovare il G-spazio transitivo più generale equivale al problema di trovare il sottogruppo di G più generale, considerando identici due sottogruppi quando sono coniugati. Questo problema può essere affrontato e risolto in molti casi speciali.
Nelle considerazioni precedenti, S era un insieme astratto e G era un gruppo astratto e nessuno dei due aveva ulteriori strutture. L'analisi diviene molto più complessa e difficile quando Gè un gruppo topologico o un gruppo di Lie e, corrispondentemente, S è dotato di strutture addizionali. Se per esempio G è un gruppo topologico, si definisce G-spazio (topologico) uno spazio topologico S che è un G-spazio nel senso definito dianzi e nel quale l'applicazione s, x ???14???[ s]x è continua da S × G a S. Se G è un gruppo di Lie, un G-spazio differenziabile è per definizione un G-spazio che è anche una ‛varietà differenziabile' e nel quale l'applicazione s, x ???14??? [s]x è ‛differenziabile' da S × G a S. Naturalmente un G-spazio differenziabile può anche considerarsi un G-spazio topologico.
Per gli spazi topologici G, la nozione di orbita e di transitività può essere definita come nel caso discreto; siamo ben lontani tuttavia dal poter ridurre lo studio dei G-spazi più o meno generali al caso transitivo. Le orbite si collegano le une alle altre in modi molto complicati, attraverso la topologia fissata in S, e la conoscenza delle componenti transitive definite dalle orbite non permette di concludere molto sulla struttura di S a meno di isomorfismi. Naturalmente, nel caso topologico, nella definizione di isomorfismo compare la condizione che ϑ sia un omeomorfismo. Quando G è compatto anche le orbite sono compatte e inoltre, quando S è uno spazio di Hausdorff, l'insieme ???44??? di tutte le orbite può essere dotata di una topologia di Hausdorff in modo naturale e i due G spazi S1 e S2 non possono essere isomorfi a meno che ???44???1 e ???44???2 siano omeomorfi. Poiché ogni spazio di Hausdorff può essere un ???44??? per un qualsiasi gruppo compatto G, il problema di classificare i possibili spazi topologici non transitivi include il. problema di classificare i possibili spazi topologici di Hausdorff. Infatti, dato un qualsiasi spazio topologico M e un qualsiasi G-spazio topologico transitivo F (per G compatto o non compatto) possiamo definire S = M × F e trasformare S in un G-spazio topologico definendo [m, f]x = m, fx. Le orbite sono allora le ‛fibre' m × F per m in M e lo spazio ???44??? di tutte le orbite è omeomorfo a M. A eccezione del caso in cui M è piuttosto banale dal punto di vista topologico, esistono G-spazi S non isomorfi a M × F (l'azione di G essendo quella descritta dianzi) nei quali l'insieme di tutte le orbite è omeomorfa a M e ogni orbita definisce un G-spazio equivalente a F. Lo studio di questi costituisce un ramo assai importante della topologia, noto come teoria degli spazi fibrati.
Quando G non è compatto, le orbite Os in S non sono necessariamente neppure chiuse e le chiusure delle orbite non soltanto non formano uno spazio topologico dotato di ‛buone' proprietà, ma non sono neppure disgiunte. Siamo per conseguenza qui molto più lontani da una classificazione completa che nel caso compatto e gran parte della teoria nota riguarda il caso speciale in cui G è il più semplice possibile, cioè il gruppo Z dei numeri interi composti per addizione o il gruppo R di tutti i numeri reali composti anch'essi per addizione. Di fatto, lo slancio iniziale allo sviluppo di questo aspetto della teoria sorge dal desiderio di comprendere l'andamento qualitativo globale delle soluzioni delle equazioni differenziali della dinamica. Indichiamo con Ω l'insieme di tutte le possibili coordinate e delle componenti dei momenti di un sistema di n particelle nello spazio. Per ogni punto ω di Ω e ogni numero reale positivo t, si può porre la questione seguente: se a un certo tempo il sistema delle particelle è nello stato descritto dal punto ω quale sarà il punto ω′ che descriverà lo stesso sistema t unità di tempo più tardi? Le leggi della dinamica affermano che ω′ è determinato unicamente da ω e t e forniscono un algoritmo che ne riduce la determinazione alla soluzione di certe equazioni differenziali. Pertanto, per ogni t esiste un'applicazione ben definita βt di Ω in Ω tale che ω′ = βt(ω). In molti casi interessanti le leggi della dinamica implicano che βt è biunivoca e surgettiva, cosicché si può definire β-t = βt-1 e trasformare Ω in un R-spazio topologico ponendo [ω]t = βt(ω). Dalle definizioni segue che βt1+t2 = βt1βt2. Effettivamente in molti casi interessanti Ω è proprio un R-spazio differenziabile. Le orbite di questo R-spazio (insieme alla loro parametrizzazione reale determinata dalle t ???14??? βt(ω)) sono naturalmente le soluzioni delle equazioni differenziali del sistema. Sia H la funzione differenziabile a valori reali su Ω che dà l'energia del sistema in funzione delle coordinate e dei momenti. H è costante sulle R-orbite e, per ogni numero reale E nel rango di H, il sottoinsieme ΩE di Ω sul quale H(ω) = E è una ‛sottovarietà' chiusa che è trasformata in se stessa e quindi è un R-spazio differenziabile. Gli R-spazi ΩE sono quelli di primaria importanza nello studio qualitativo della soluzione delle equazioni differenziali della dinamica, che fu iniziato da Poincaré verso la fine dell'Ottocento e proseguito nel nostro secolo da G. D. Birkhoff. Molti dei loro risultati possono considerarsi casi speciali di teoremi su gruppi più generali di trasformazioni topologiche. La formulazione e la dimostrazione di alcuni di questi teoremi più generali occupa ampio spazio nella letteratura matematica. Per ovvie ragioni a queste ricerche si dà spesso il nome di ‛dinamica topologica'. Più recentemente, S. Smale, insieme con allievi e collaboratori, ha affrontato energicamente i problemi lasciati aperti da Birkhoff servendosi di strumenti nati dallo sviluppo successivo della topologia, formulando il problema come quello di classificare G-spazi differenziabili a meno di isomorfismi (differenziabili).
Nella formulazione originale di Lie, lo studio dei gruppi di trasformazioni era un problema ‛locale'. Si studiavano le trasformazioni puntuali in un piccolo intorno dell'identità di G e si riduceva lo studio all'esame della relazione fra l'algebra di Lie di G e i ‛campi di vettori' su S. Uno studio molto dettagliato della relazione tra problemi globali e locali fu compiuto verso la metà del 1950 da R. S. Palais.
Un fatto importante relativo alle equazioni differenziali della dinamica è che esiste una misura naturale ζ, definita sui sottoinsiemi di Borel dello spazio delle fasi Ω, la quale è invariante rispetto alle trasformazioni βt. Questo fatto è noto come teorema di Liouville e la misura ζ si chiama talvolta ‛misura di Liouville'. A questa misura è inoltre associata una famiglia di misure invarianti ζE portate dalle ipersuperfici di energia costante ΩE. Pertanto gli R-spazi ΩE studiati nella teoria dei sistemi dinamici posseggono misure invarianti ζE. Nei casi di maggiore interesse ΩE è compatto e ζE(ΩE) è finita.
Nel 1931 B. O. Koopmann osservò molto acutamente che la misura invariante ζE in ΩE può essere usata per definire una rappresentazione unitaria UE di R, nello stesso modo in cui la misura di Haar in un gruppo serve a definire la rappresentazione regolare di tale gruppo. Si forma L2(ΩE, e si pone per definizione
UEtf(a) = f(βt(a)).
Applicando il teorema di Stone (dimostrato nel 1930) si può scrivere:
UEt = eitHE,
associando così una famiglia di operatori autoaggiunti HE a ogni sistema dinamico.
L'idea di Koopmann era quella di usare i fatti noti relativamente alla classificazione degli operatori autoaggiunti (v. sopra, cap. 8) per classificare i sistemi dinamici. Questa osservazione suggerì a von Neumann la possibilità di usare i metodi della geometria degli spazi di Hilbert per studiare le relazioni fra le ‛medie spaziali'
e le ‛medie temporali'
delle funzioni di Borel f a valori reali su ΩE. Questo problema ha le sue radici nei fondamenti di quella parte della fisica teorica nota come meccanica statistica e aveva occupato i fisici fin dal momento della sua formulazione nel 1870. Von Neumann riuscì a dimostrare che quando ζE(ΩE) è finito e f sta in L2(ΩE, ζE) la media temporale esiste nel senso della convergenza in norma in questo spazio di Hilbert e inoltre la media temporale eguaglia la media spaziale purché sia soddisfatta una certa condizione nota come ‛ergodicità' o ‛transitività metrica'. Prendendo spunto dal teorema di von Neumann, G. D. Birkhoff dimostrò il seguente teorema assai più difficile: se f è sommabile rispetto a ζE, allora
esiste per tutti gli ω a eccezione di quelli contenuti in un insieme di ζE-misura zero e, se vale la transitività metrica, la funzione di ω che ne risulta è costante a eccezione che in un insieme di ζE-misura nulla e questa costante è uguale alla media spaziale di f. Questi teoremi di von Neumann e Birkhoff sono noti rispettivamente come ‛teorema della media ergodica' e ‛teorema ergodico puntuale'. La loro formulazione e dimostrazione portò in un lasso di tempo relativamente breve alla creazione della ‛teoria ergodica' come nuovo ramo della matematica.
Nella formulazione e dimostrazione dei teoremi ergodici, la struttura topologica e differenziabile di ζE non ha un ruolo diretto. Entra in gioco soltanto la misura ζE e la famiglia degli insiemi di Borel sui quali è definita. Lo stesso vale per il concetto centrale di transitività metrica che definiremo tra poco. Di fatto, il significato di questo concetto chiave si può forse meglio apprezzare prendendo lo spunto da queste osservazioni e introducendo G-spazi S, ove S è uno ‛spazio di misura' piuttosto che una varietà o uno spazio topologico.
Uno ‛spazio di Borel' è per definizione un insieme S nel quale si assegni una famiglia ℬ di sottoinsiemi, che si chiamano ‛sottoinsiemi di Borel' di S, tali che: a) se E1, E2, ... stanno in ℬ anche l'insieme
di tutti gli s che sono comuni a tutti gli EJ è in ℬ; b) se E è in ℬ anche S − E è in ℬ; c) S è in ℬ. Ne segue naturalmente che l'insieme vuoto è in ℬ e che l'insieme
di tutti gli s contenuti almeno in un Ej è un elemento di ℬ. Una funzione f da uno spazio di Borel S1 a uno spazio di Borel S2 si chiama ‛funzione di Borel' se l'insieme f-1(E) di tutti gli s con f(s) in E è un insieme di Borel in S1 ogniqualvolta E è un insieme di Borel in S2. Se f è biunivoca e surgettiva e f e f-1 sono entrambe funzioni di Borel, si dice che f è un isomorfismo di Borel. Quando una tale f esiste, si dice che S1 e S2 sono ‛spazi di Borel isomorfi'. Ogni spazio topologico può essere trasformato in uno spazio di Borel in modo canonico prendendo come insiemi di Borel gli elementi della più piccola famiglia di insiemi che contiene gli insiemi aperti e soddisfa le condizioni a) e b) che abbiamo poc'anzi enunciato. Inoltre ogni sottoinsieme S1 di uno spazio di Borel S diviene uno spazio di Borel quando si prendano come sottoinsiemi di Borel di S1 gli insiemi S1 ⋂ E al variare di E fra i sottoinsiemi di Borel di S. Risulta che, se S1 è un sottoinsieme di Borel di un gruppo localmente compatto e separabile e se S1 è più che numerabile, S1 è isomorfo come spazio di Borel all'intervallo unità sulla retta reale. Molti altri spazi di Borel che si presentano nella pratica godono di questa proprietà. Non si perde molto in generalità se si restringe l'attenzione agli spazi di Borel che sono standard, nel senso che sono isomorfi come spazi di Borel all'intervallo unità, oppure hanno al più una famiglia numerabile di elementi e ogni loro sottoinsieme è un insieme di Borel. Se S1 e S2 sono spazi di Borel, lo spazio S1 × S2 di tutte le coppie s1, s2 con s1 in S1 e s2 in S2 diventa uno spazio di Borel quando si prenda come famiglia di insiemi di Borel la più piccola famiglia di insiemi che soddisfino le condizioni a) e b) della definizione e contengano tutti gli insiemi del tipo E1 × E2, ove E1 ed E2 sono sottoinsiemi di Borel rispettivamente di S1 e S2. Si vede facilmente che S1 × S2 è standard quando S1 e S2 sono anch'essi standard.
Dato un gruppo separabile localmente compatto G, si definisce come ‛G-spazio di Borel standard' un G-spazio S il quale è anche uno spazio di Borel in modo tale che s, x ???14??? sx sia una funzione di Borel da S × G a S. Una misura σ-finita μ nel G-spazio di Borel standard S si dice ‛invariante' se μ(Ex) = μ(E) per tutti gli x in G e tutti i sottoinsiemi di Borel in S. Essa si dice ‛quasi invariante' se μ e la misura E ???14??? μ(Ex) hanno gli stessi insiemi di misura nulla per tutti gli x in G. Una ‛classe di misure invarianti' è una famiglia di misure quasi invarianti costituita da tutte le misure σ-finite che hanno gli stessi insiemi di misura nulla di tutte le altre. Per definizione, un ‛G-spazio di misura' è una coppia costituita da un G-spazio di Borel standard S e da una classe di misure invarianti C in S. Due G-spazi di misura S1, C1 e S2, C2 si dicono ‛isomorfi' o ‛coniugati' se esistono degli insiemi di Borel N1 e N2, rispettivamente in S1 e S2, tali che Nj sia G-invariante e di misura zero rispetto a Cj, per j = 1 e j = 2, e un isomorfismo di Borel ϕ di S1 − N1 su S2 − N2 tale che ϕ(sx) = ϕ(s)x per tutti gli s in S1 − N1 e tutti gli x in G e tale inoltre che E sia di misura nulla rispetto a C1 se, e soltanto se, ϕ(E) ha misura nulla rispetto a C2.
Se S, C è un G-spazio di misura e S1 è un sottoinsieme di Borel G-invariante di S che non ha misura nulla rispetto a C, S1, C1 è un Gpazio di misura, ove C1 è l'insieme di tutte le restrizioni a S1 delle misure in C. Se anche S2 = S − S1 è di misura non nulla, S, C è coniugato in senso ovvio alla ‛somma diretta' di S1, C1 e S2, C2. Un G-spazio di misura S, C si chiama ‛ergodico' o ‛metricamente transitivo' se non è coniugato a una somma diretta di due G-spazi di misura non banali o, equivalentemente, se, per ogni sottoinsieme di Borel G-invariante S1 di S, o S1 o S − S1 ha una C-misura nulla. Così come ogni G-spazio discreto è isomorfo a una somma diretta di G-spazi transitivi, anche ogni G-spazio di misura è, in un certo senso, un ‛integrale diretto' di G-spazi di misura che sono metricamente transitivi o ergodici. Questa decomposizione in integrale diretto è essenzialmente unica e il fatto che essa esista riduce gran parte delle questioni sui G-spazi di misura al caso speciale in cui il G-spazio di misura è ergodico. La situazione qui è in netto contrasto con quella dei G-spazi topologici per i quali non esiste una riduzione siffatta. Almeno in parte questa differenza può attribuirsi al fatto che spazi di misura ‛non patologica' sono più o meno tutti simili, mentre questo non è assolutamente il caso per gli spazi topologici.
Sia ora S, C un G-spazio di misura ergodico e consideriamo le orbite di G in S. Si può dimostrare che queste sono tutte insiemi di Borel e quindi che al più una ha misura positiva. Se esiste un'orbita di misura positiva, il suo complemento ha necessariamente misura zero e S, C è coniugato a S′, C′ ove S′ è un G-spazio di Borel standard e ‛transitivo'. Si dice in questo caso che S, C è ‛essenzialmente transitivo'. Nel caso contrario, in cui ogni orbita ha misura nulla, si dice che il G-spazio di misura S, C è ‛propriamente ergodico'. Per ogni sottogruppo chiuso H di G, lo spazio G/H di tutte le classi laterali destre diventa un insieme di Borel standard quando si definiscano come insiemi di Borel quegli insiemi le cui immagini inverse in G sono insiemi di Borel in G e si definisca (Hx)y = Hxy. Questo spazio di Borel standard ammette un'unica classe di misura invariante C e ogni G-spazio di misura di Borel essenzialmente transitivo è coniugato a uno del tipo G/H, C. Così come i G-spazi discreti transitivi sono completamente classificati dalle classi di coniugio di sottogruppi di G, i G-spazi di misura essenzialmente transitivi sono completamente classificati dalle classi di coniugio di sottogruppi chiusi di G.
Se tutti i G-spazi di misura ergodici fossero essenzialmente transitivi, la teoria dei Gspazi di misura si ridurrebbe, per il teorema di decomposizione, a un miscuglio poco interessante e abbastanza banale di pura teoria della misura e di teoria dei gruppi applicate allo spazio quoziente G/H. Questo è ciò che accade effettivamente quando G è compatto. Non vi sono G-spazi di misura propriamente ergodici, qualunque sia il gruppo compatto. D'altra parte, per ogni gruppo localmente compatto e separabile G il quale non sia compatto, G-spazi propriamente ergodici esistono in grande quantità. Essi costituiscono un nuovo tipo di oggetti matematici il cui studio non può essere ricondotto a null'altro. Lo studio di questi oggetti costituisce il tema principale della cosiddetta ‛teoria ergodica'. La loro classificazione rappresenta un problema affascinante che dopo quaranta anni è ancora ben lontano dall'essere risolto, persino nel caso in cui G sia il gruppo additivo degli interi. D'altra parte tali oggetti sono, in un senso ovvio, analoghi ai sottogruppi chiusi di G. Di fatto numerosi risultati di teoria dei gruppi inducono a porli sullo stesso piano dei sottogruppi veri e propri.
Sia S, e un G-spazio di misura ergodico per il gruppo G separabile e localmente compatto. Se C contiene una misura invariante μ, questa misura è unica a meno del prodotto per una costante e si può costruire una rappresentazione unitaria U di G in L2(S, μ) ripetendo la costruzione di Koopmann alla quale abbiamo accennato precedentemente: Ux(f)(s) = f(sx). Servendosi dello stesso artificio usato per definire rappresentazioni indotte quando G/H non ammette una misura invariante, si può associare una rappresentazione unitaria US,C a ogni Gspazio di misura ergodico S, C. Chiaramente la classe di equivalenza di US,C dipende soltanto dalla classe di coniugio di S, C e si riduce a quella della rappresentazione unitaria di G indotta dalla rappresentazione identità di H quando S è transitivo e coniugato a G/H. Quando G è commutativo e US,C è una somma diretta discreta di elementi di Ø, si dice che S, C ha uno ‛spettro puramente puntuale'. Gli elementi di Ø che compaiono in tale somma hanno ivi molteplicità uno e formano un sottogruppo numerabile Γ di Ø chiamato ‛spettro' del G-spazio S, C. Si dimostra facilmente che S, C quando ha uno spettro puramente puntuale, è determinato, a meno di un coniugio, dal suo spettro e che in esso compare effettivamente ogni sottogruppo numerabile di Ø. Un G-spazio ergodico con spettro puramente puntuale è propriamente ergodico se, e soltanto se, Γ non è chiuso.
Per costruire un G-spazio ergodico con spettro Γ, sia S = ???45??? e osserviamo che il duale dell'omomorfismo di iniezione di Γ in Ø è un omomorfismo ϑ di G in ???45???, cosicché, per χ in ???45???, possiamo definire [χ]x = χ(ϑ(x)). Naturalmente C è la classe di misura della misura di Haar in ???45???.
È molto facile costruire G-spazi ergodici che non hanno spettro puramente puntuale quando G è numerabile e discreto. In questo caso, per ogni gruppo K commutativo compatto, si può costruire il gruppo KG di tutte le funzioni da G a K e farlo diventare un G-spazio, ponendo per definizione [f]x = f′, ove f′(y) = f(y-1x). KG è esso stesso un gruppo compatto in un'opportuna topologia naturale e la classe della misura di Haar in KG lo fa divenire un G-spazio ergodico. Si può dimostrare che la rappresentazione unitaria U associata a questo G-spazio è la somma diretta di un'identità a una dimensione e di una famiglia numerabile di repliche della rappresentazione regolare di G. Si osservi che U è indipendente dalla scelta di K e questo suggerisce che forse la classe di coniugio di [KG, classe della misura di Haar] è anch'essa indipendente da K. Stabilire se questo sia vero o no quando G è il gruppo additivo Z degli interi e K varia fra i gruppi ciclici di ordine n è rimasto per più di venti anni un problema insoluto. Tuttavia, nel 1959, Kolmogoroff e Sinai, ispirandosi al concetto di ‛entropia' della nuova teoria dell'informazione, dimostrarono come si potesse definire l'‛entropia' per ogni spazio ergodico Z. È ovvio che l'entropia dipende soltanto dalla classe di coniugio dello spazio e si può dimostrare che l'entropia di [KZ, classe della misura di Haar] è uguale a log n ogniqualvolta K ha n elementi. D'altra parte gli Z-spazi con spettro puramente puntuale hanno entropia zero, cosicché l'entropia e la rappresentazione U tendono a essere invarianti complementari. Recentemente, in un importante lavoro, Ornstein ha dimostrato che gli elementi di un'ampia classe di Z-spazi ergodici interessanti nella teoria della probabilità sono coniugati se, e soltanto se, hanno la stessa entropia.
Gli analoghi dei G-spazi di misura [K0, classe della misura di Haar] quando Gnon è numerabile e discreto sono alquanto più difficili da descrivere. La loro costruzione dipende dalla nozione probabilistica di ‛indipendenza' per ‛variabili casuali' e da un'idea fondamentale di N. Wiener che, nel 1920, dimostrò che è possibile assegnare ‛variabili casuali' ft a ogni intervallo finito I, in modo tale che fI1, ..., fIk, siano ‛indipendenti' ogniqualvolta gli Ij sono disgiunti; così ogni FI ha una distribuzione ‛gaussiana' la cui ‛media' è zero e la cui ‛varianza' dipende soltanto dalla lunghezza di I. Identificando, se necessario, punti in Ω, si può supporre che le fI separino i punti di Ω; si può allora dimostrare che esiste, ed è essenzialmente unica, un'azione della retta reale su Ω la quale conserva μ ed è tale che fI([ω)t) = fI+t(a). Questa azione è ergodica ed è l'analogo dell'azione di G su [K0, classe della misura di Haar] per il caso in cui G sia la retta reale. Più in generale, dato un G-spazio transitivo M con una misura invariante ν, si dimostra che il risultato di Wiener vale per variabili casuali parametrizzate dai sottoinsiemi di Borel di M aventi misura finita. È importante osservare che ogni G-spazio differenziabile ammette una classe di misure canonicamente invarianti e quindi un G-spazio di misura associato.
12. Teoria dei gruppi e topologia.
Come abbiamo accennato nell'introduzione, i concetti della teoria dei gruppi hanno sostenuto un ruolo importante nella moderna topologia combinatoria (algebrica) fin dal momento in cui, nel 1895, Poincaré la inventò. Di fatto, una delle strategie sistematicamente applicate nello studio della topologia algebrica è stata quella di associare a ogni spazio topologico sufficientemente regolare certi gruppi e famiglie di gruppi in un modo ‛intrinseco' e quindi ricondurre problemi relativi allo spazio a problemi relativi al gruppo a esso associato. D'altro canto, i gruppi di Lie e gli spazi quozienti G/H, ove G è un gruppo di Lie e H è un sottogruppo chiuso, sono anch'essi spazi topologici; scoprire le proprietà topologiche di questi spazi è stato uno dei maggiori impegni per la topologia e al tempo stesso uno dei campi in cui si sono ottenuti i maggiori successi. Naturalmente, la scoperta di queste proprietà deve considerarsi anche una parte importante dello studio del gruppo di Lie G e del G-spazio transitivo G/H. L'esperienza, infine, ha dimostrato che gruppi e spazi topologici possono essere utilmente considerati come oggetti matematici analoghi. Abbiamo già osservato nel cap. 10 come sia possibile associare gruppi di coomologia a gruppi e a spazi topologici. D'altronde, la scoperta della ‛k-teoria' da parte di Grothendieck e di Atiyah e Hirzebruch, nel 1958 e nel 1961, mostra che si ha un analogo della teoria delle rappresentazioni per gli spazi topologici. Similmente si possono considerare ‛i fibrati principali' con gruppo G su uno spazio topologico B come un analogo topologico di un omomorfismo di un gruppo G′ nel gruppo G, Teoria dei gruppi e topologia sono rami della matematica strettamente connessi tra loro.
Per definizione, uno ‛zero simplesso' nello spazio Rn di tutte le n-uple di numeri reali è un punto. Per definizione, un k simplesso è l'insieme di tutti i punti sui segmenti di retta che congiungono i punti di un k − 1 simplesso con un punto non appartenente all'iperpiano di dimensione k − 1 contenente il simplesso di dimensione k − 1. Per ogni k simplesso esistono esattamente k + 1 punti, detti vertici del k simplesso, i quali non stanno in nessun segmento contenuto nel k simplesso. Inoltre, per ogni vertice di un k simplesso esiste uno e un solo k − 1 simplesso i cui vertici sono i k vertici restanti del k simplesso. Questi k + 1, k − 1 simplessi vengono chiamati ‛facce' del k simplesso. I possibili ordinamenti P1, P2, ..., Pk+1 dei vertici di un k simplesso si dividono in due classi tali che gli elementi della stessa classe possono essere trasformati l'uno nell'altro mediante un numero pari di trasposizioni. Si ‛orienta' un k simplesso, con k > 0, scegliendo una di queste due classi di ordinamenti. Ciascuna di esse contiene un elemento O in cui un dato vertice occupa il primo posto e, omettendo questo vertice, si ottiene un ordinamento della faccia corrispondente la cui classe dipende solamente dalla classe di O. In questo modo un orientamento di un k simplesso induce un orientamento in ciascuna delle sue facce, ogniqualvolta sia k ≥ 2.
Per definizione, un ‛complesso simpliciale finito' è una famiglia costituita da un numero finito di simplessi tale che due elementi qualsiasi di questa famiglia si intersechino in un simplesso di dimensione inferiore, i cui vertici siano i vertici dei due simplessi intersecantisi. Dato un complesso simpliciale finito, un intero positivo k e un gruppo commutativo G (con + come operazione di gruppo), si chiama ‛k catena a coefficienti in G' una funzione f dai simplessi orientati nel complesso a G, tale che f(σ) = −f(σ′) ogniqualvolta σ e σ′ sono lo stesso simplesso con orientazioni opposte. Una ‛zero catena' con coefficienti in G è semplicemente una funzione dai vertici del complesso a G. Le k catene, per k = 0, 1, 2, ..., formano chiaramente un gruppo rispetto all'addizione puntuale. Per definizione, la frontiera ∂σ di un k simplesso orientato è la k − 1 catena con coefficienti interi che assegna 1 o −1 a ciascun k − 1 simplesso orientato associato a una faccia di σ a seconda che la sua orientazione sia quella indotta da σ o l'opposta e che assegna zero a ogni k − 1 simplesso che non sia una faccia di σ. Quando σ è un 1 simplesso orientato, ∂σ assegna −1 al primo vertice, 1 al secondo e zero a tutti gli altri zero simplessi. Si osservi che per ogni k catena f, f(σ) ∂σδ è indipendente dall'orientazione del simplesso σ, cosicché ha senso formare la somma degli f(σ) ∂σ su tutti i k simplessi (non orientati). Questa somma si chiama frontiera ∂f della k catena f. Evidentemente l'applicazione f ???14??? ∂f è un omomorfismo del gruppo delle k catene nei gruppo delle k − 1 catene. Le k catene nel nucleo di questo omomorfismo si chiamano ‛k cicli' e le k − 1 catene nel rango di esso si chiamano ‛k − 1 frontiere' o ‛k − 1 bordi'. Si dimostra che ∂∂f ≡ 0 cosicché ogni k − frontiera è necessariamente un k − 1 ciclo. Solo eccezionalmente vale l'inverso di questo fatto e, per definizione, il ‛k-esimo gruppo di omologia' del complesso con coefficienti in G è il quoziente del gruppo dei k cicli per il sottogruppo delle k frontiere. Quando G è il gruppo additivo degli interi, Z, si può dimostrare che il k-esimo gruppo di omologia è isomorfo a Z × Z × ... × Z (nk volte) × Fk, ove Fk è finito e nk è un intero non negativo che prende il nome di k-esimo numero di Betti del complesso. Conoscere completamente i gruppi di omologia significa conoscere i numeri di Betti e i gruppi commutativi finiti Fk. Un teorema fondamentale afferma che i gruppi di omologia di un complesso sono ‛invarianti topologici', esattamente nel senso seguente: siano ℳ1 e ℳ2 gli insiemi di punti unioni dei simplessi nei due complessi. Se ℳ1 e ℳ2 sono omeomorfi come spazi topologici, i loro k-esimi gruppi di omologia con coefficienti in G sono isomorfi per ogni k e ogni G. In altre parole, è possibile associare gruppi di omologia ben definiti a qualsiasi spazio topologico che sia omeomorfo all'insieme dei punti contenuto in un complesso. Quando si sceglie un tale omeomorfismo con un complesso particolare si opera una ‛triangolazione' dello spazio. Il teorema di invarianza non è affatto banale e una dimostrazione completa si ebbe soltanto nel 1915. In ricerche più recenti, vennero introdotte altre definizioni dei gruppi di omologia che potevano applicarsi a classi più generali di spazi e che resero l'invarianza topologica un fatto manifesto. Tuttavia, la definizione originale chiarisce la natura essenziale dei gruppi di omologia e gli spazi triangolabili includono molti degli esempi più importanti.
Strettamente collegati ai gruppi di omologia sono i ‛gruppi di coomologia' che vennero introdotti intorno al 1930. Si definisce il ‛cobordo' δf di una k catena in modo molto simile a quello in cui si definisce il bordo, eccetto che il cobordo è una k + 1 catena invece che una k − 1 catena e il cobordo di un k simplesso è diverso da zero su quei k + 1 simplessi dei quali il k simplesso dato è una faccia. Si dimostra che δδf ≡ 0 e da questo punto si procede esattamente come nella definizione dei gruppi di omologia. Quando G è un gruppo topologico, è possibile definire in modo naturale nei gruppi delle cocatene una struttura di gruppi topologici. Questi sono separabili e localmente compatti quando G è separabile e localmente compatto e altrettanto accade per i corrispondenti gruppi di omologia e comologia. Si rileva inoltre che il duale di Pontrjagin Hk(G) del k-esimo gruppo di omologia Hk(G) di un complesso a coefficienti in G è canonicamente isomorfo al gruppo di coomologia Hk(Ø) di quel complesso a coefficienti nel duale di Pontrjagin G di G. Di fatto Pontrjagin stabilì il suo teorema di dualità pensando a questo tipo di applicazioni alla topologia.
Più facili da definire, ma molto più difficili da calcolare, sono i gruppi di omotopia πn introdotti nel 1935 da W. Hurewicz. Dati due spazi topologici X e Y e due funzioni continue f e g che applicano X in Y, si dice che f e g sono ‛omotope' se esiste un'applicazione continua ϕ di I × X in Y, ove I è l'intervallo unità, tale che ϕ(0, x) ≡ f(x) e ϕ(1, x) ≡ g(x). Intuitivamente f e g sono omotope se f può essere ‛deformato con continuità' in g. Ora, se X è la ‛n sfera' Sn, cioè lo spazio topologico compatto costituito dalle (n + 1)-uple di numeri reali tali che
x²1 + x²2 + ... + x²n+1 = 1,
esiste un modo naturale di definire una ‛moltiplicazione' per applicazioni in modo che la classe di omotopia del prodotto dipenda soltanto dalle classi di omotopia dei fattori. In questo modo l'insieme πn di tutte le classi di omotopia delle applicazioni di Sn in Y diventa un gruppo, che viene chiamato l'n-esimo gruppo di omotopia πn(Y) di Y. (Di fatto si scelgono punti fissi s e y, in S e Y rispettivamente, e si concentra l'attenzione sulle applicazioni che mandano s in y. Il risultato è indipendente da s e in molti casi è anche indipendente da y). Si vede facilmente che πn(Y) è commutativo quando n > 1 e che π1(Y) coincide con il gruppo fondamentale definito da Poincaré.
Una volta definiti i gruppi di omologia e di omotopia, si pone il problema di determinare la loro struttura per vari spazi d'interesse concreto. Questi comprendono senza dubbio gli spazi topologici dei gruppi di Lie e dei loro spazi quozienti. D'altra parte, la determinazione dei gruppi di omologia e di omotopia dello spazio topologico di un gruppo di Lie deve essere considerata come una parte del problema di determinare la sua struttura come gruppo di Lie. Similmente, la determinazione dei gruppi di omologia e di omotopia di uno spazio quoziente deve essere considerata come una parte dello studio della struttura del gruppo di trasformazione associato. Allo stesso modo in cui si cerca di comprendere la struttura di gruppi complicati costruendoli a partire da gruppi semplici, così si cerca di comprendere la struttura di spazi topologici costruendoli a partire da spazi semplici. In particolare, si cerca di collegare i gruppi di omologia e di omotopia di tutto lo spazio a quelli delle componenti; i teoremi corrispondenti sostengono un ruolo importante nella ricerca, in casi particolari, di tali gruppi. Altre questioni che si pongono in modo naturale concernono da un lato le relazioni fra gruppi di omologia e coomologia tra loro e con i gruppi di omotopia e dall'altro la misura in cui uno spazio topologico è determinato quando ne siano noti i gruppi di omologia e di omotopia. Dare risposte parziali con vari gradi di completezza a questi problemi è stata una delle maggiori preoccupazioni dei topologhi negli ultimi quarant'anni. Un'esposizione relativamente completa dei risultati finora ottenuti non può essere fatta in un articolo di questa estensione; tuttavia, vale forse la pena di dare qualche breve indicazione.
Prima di tutto esiste una nozione più grossolana di quella di omeomorfismo, chiamata ‛tipo di omotopia', in base alla quale due spazi dello stesso tipo di omotopia hanno gruppi di omologia, coomologia e omotopia isomorfi. Si dice che X e Y hanno lo stesso ‛tipo di omotopia' se esistono funzioni continue f e g, da X a Y e da Y a X rispettivamente, tali che le funzioni x ???14??? g(f(x)) e y ???14??? f(g(y)) siano omotope all'identità, rispettivamente in X e in Y. Si rileva immediatamente che lo spazio Rn di tutte le n-uple ordinate di numeri reali, con la topologia usuale, è dello stesso tipo di omotopia dello spazio ridotto a un punto e che X1 × Y1 è dello stesso tipo di omotopia di X × Y quando X e X1 (rispettivamente Y e Y1) hanno lo stesso tipo di omotopia. Poiché ogni gruppo di Lie connesso è omeomorfo al prodotto diretto di Rn, per un opportuno n, e di un gruppo di Lie compatto connesso, ne segue che, nello studiare l'omologia e l'omotopia dei gruppi di Lie, ci si può limitare ai gruppi compatti. Per gli spazi quozienti la situazione è più complicata e verrà esaminata brevemente fra poco.
La costruzione del prodotto diretto fra spazi è, naturalmente, analoga alla costruzione del prodotto diretto fra gruppi. I gruppi di omotopia si comportano in un modo relativamente semplice rispetto al prodotto diretto. Si dimostra facilmente che, per ogni k, πk(X × Y) è isomorfo al prodotto diretto di πk(X) e πk(Y). I gruppi di omologia e coomologia per X, Y e X × Y sono legati fra loro in modo piuttosto complicato; qualche idea in proposito si può ottenere in modo semplice ed elegante dalla formula che lega i loro numeri di Betti. Per definizione, il polinomio di Poincaré di uno spazio è il polinomio a0 + a1t + a2t2 + ... + antn, ove ak è il k-esimo numero di Betti. Si dimostra che il polinomio di Poincaré di X × Y è il prodotto dei polinomi di Poincaré di X e Y rispettivamente.
La nozione di estensione di un gruppo per un altro, cioè un gruppo G con un dato sottogruppo normale N e quoziente Q, ha una nozione equivalente nella teoria degli spazi topologici. È questa la nozione di ‛spazio fibrato' con una data base B e una data fibra F. Grosso modo, esso è uno spazio topologico X che ammette un'applicazione continua ϕ su B, di tipo tale che, per ogni b in B, l'insieme ϕ-1(b) sia omeomorfo a F. Tuttavia, per ottenere dei teoremi interessanti, occorre imporre ulteriori restrizioni a X e a ϕ. Si osservi che, come il caso più elementare di un'estensione di un gruppo Q per un gruppo N è il prodotto diretto Q × N, così il prodotto diretto B × F è il caso più elementare di uno spazio fibrato con base B e fibra F. Una ‛struttura fibrata' è un caso particolare di spazio fibrato nel quale s'impone la condizione addizionale che sia possibile trovare una famiglia {Oα} di sottoinsiemi aperti di B tale che ϕ-1(Oα) sia omeomorfo a Oα × F; in modo che ϕ-1(b) sia mandato su b × F per ogni b. Intuitivamente, una struttura fibrata è ‛localmente un prodotto diretto'. Di fatto, la teoria delle strutture fibrate mira a un raffinamento della nozione appena descritta, in cui è dato a priori un gruppo topologico G di omeomorfismi di F su se stesso e si vuole che gli omeomorfismi di ϕ-1(b) su b × F che abbiamo considerato dianzi siano tali che, ciascuno di essi, combinato con l'inverso di un altro, definisca un elemento di G. Quando F è esso stesso un gruppo topologico e G è il gruppo di tutte le sue traslazioni sinistre, si dice che si ha a che fare con una ‛struttura fibrata principale'.
La teoria delle strutture fibrate ebbe inizio intorno al 1935 ed ebbe un considerevole sviluppo nei 15 anni successivi a opera di Whitney, Hopf, Stiefel, Ehresmann e altri. Essa insisteva soprattutto sul problema analogo a quello dell'estensione di un gruppo; il problema cioè di trovare la struttura più generale con una data base, una data fibra e un dato gruppo. Tale problema può ridursi al caso in cui la struttura è principale, così che gruppo e fibra coincidono. Questo sviluppo si trova esposto nel volume di N. Steenrod The topology of fiber bundles apparso nel 1951. Un risultato chiave, il cosiddetto ‛teorema del ricoprimento dell'omotopia', afferma che una deformazione continua, o omotopia, di applicazioni di uno spazio Y nella base B di una struttura fibrata X può essere ‛rialzata' a una deformazione continua di applicazioni di Y in X ogniqualvolta l'applicazione iniziale può essere rialzata. Servendosi di questo teorema, si trova una relazione abbastanza semplice fra i gruppi di omotopia di B, X e F; la quale generalizza la relazione stabilita precedentemente per il prodotto diretto. Questo teorema afferma l'esistenza di una successione di omomorfismi ∂k, ik, pk, ove ∂k applica πk+1(X) in πk(F), ik applica πk(F) in πk(X) e pk applica πk(X) in πk(B); la successione è ‛esatta' nel senso che il rango di ogni omomorfismo coincide con il nucleo di quello che lo segue. Ciò implica che ogni gruppo di omotopia è un'estensione di un gruppo mediante un altro, questi gruppi essendo isomorfi a coppie in un modo ben definito. Come abbiamo precedentemente osservato, la semplice relazione secondo la quale πk(X ×Y) è isomorfo a πk(X) × πk(Y) si complica notevolmente quando si passa dai gruppi di omotopia a quelli di omologia e coomologia, oppure quando si passa dai prodotti diretti alle strutture fibrate. Quando si considerano questi due casi simultaneamente e si cerca di collegare l'omologia e la coomologia di una struttura fibrata a quelle della base e di una fibra, le complicazioni si moltiplicano in modo tale che per lungo tempo non fu possibile compiere alcun progresso. Verso il 1945, questo ostacolo fu finalmente rimosso da ricerche di Leray che acquistarono grande notorietà attraverso raffinamenti e applicazioni eseguiti da J. P. Serre nella sua tesi pubblicata verso il 1951. Lo strumento fondamentale di Leray era una costruzione algebrica, nota come successione spettrale, che può essere grossolanamente descritta come una doppia successione di successioni esatte collegate fra loro. Leray aveva lavorato con spazi fibrati più generali delle strutture fibrate, ma, per le applicazioni che aveva in mente, Serre aveva bisogno di qualcosa di ancor più generale e lo trovò in quegli spazi fibrati per i quali vale il teorema di ricoprimento dell'omotopia ogniqualvolta Y sia un simplesso. Spazi fibrati in questo senso si considerano oggi oggetti di studio ‛naturali'.
Un risultato, noto ormai da lungo tempo, relativo alla topologia dei gruppi di Lie compatti connessi è il teorema di H. Weyl, secondo il quale il gruppo fondamentale è finito purché il gruppo di Lie sia semisemplice. Ne segue che il più generale fra tali gruppi può essere ottenuto come quoziente, per un sottogruppo finito del suo centro, del prodotto diretto di un numero finito di gruppi, ciascuno dei quali sia un toro a una dimensione (il gruppo delle rotazioni del piano) oppure un gruppo compatto semplicemente connesso avente un'algebra di Lie semplice. In particolare, i numeri di Betti di due gruppi di Lie compatti localmente isomorfi coincidono. Lo studio dei numeri di Betti fu iniziato da E. Cartan e, intorno alla metà del 1930, i polinomi di Poincaré per i gruppi compatti classici come per i gruppi eccezionali di dimensioni più basse erano stati tutti calcolati. Per esempio, il polinomio di Poincaré di SU(n + 1) per n ≥ 1 è
(1 + t3)(1 + t5) ... (1 + tn+1)
e valgono formule simili per le altre tre famiglie infinite. Dei rimanenti gruppi eccezionali si occupò nel 1949 C. T. Yen, mentre, poco più tardi, Weil e Chevalley scoprirono metodi più semplici per trattare tutti i casi.
Le ricerche sulla ‛torsione' (cioè le componenti finite dei gruppi di omologia e coomologia intera) per gruppi di Lie compatti rimasero frammentarie finché non si rese disponibile lo strumento della successione spettrale. Ciò accadde anche per i numeri di Betti degli spazi quozienti dei gruppi di Lie compatti. Servendosi delle successioni spettrali e di altre tecniche, A. Borel ottenne, in entrambi i casi, ampi risultati, esposti nella sua tesi del 1952 (che venne pubblicata nel 1953). Questi risultati sono troppo complicati e ricchi di dettagli per poter essere descritti qui. Basti dire tuttavia che un gruppo di Lie G, compatto connesso con sottogruppo connesso chiuso H, è una struttura fibrata principale con fibra H e base G/H. Pertanto i risultati già noti su G e H conducono, mediante le successioni spettrali, a risultati sull'omologia di G/H. Borel applicò anche in notevole misura il concetto di ‛spazio classificante'. Sia n un intero positivo e sia G un gruppo di Lie compatto. Non è difficile stabilire l'esistenza di strutture fibrate principali connesse per archi, X, con gruppo G, per le quali πi(X) è banale per 1 ≤ i ≤ n. Tale X si dice ‛universale' per G e n e la sua base B si dice ‛classificante' per G e n. Mentre X e B non sono univocamente determinati da G e n, i j-esimi gruppi di omologia e coomologia di B sono univocamente determinati per j = 1, 2, ..., n e inoltre sono indipendenti da n. Pertanto, senza fissare n ha senso parlare di un gruppo di omologia e coomologia dello spazio classificante di un gruppo di Lie compatto. Si possono trovare spazi classificanti per i gruppi compatti classici fra gli oggetti geometrici la cui struttura è nota e determinare così la loro omologia e coomologia. Gli spazi classificanti vennero introdotti fin dai primi tempi della teoria delle strutture fibrate in quanto essi si rivelarono utili nella classificazione ditali strutture. Dato uno spazio X di tipo opportunamente ristretto, le strutture fibrate principali essenzialmente differenti con gruppo G corrispondono biunivocamente in modo naturale alle classi di omotopia delle applicazioni continue di X in uno spazio classificante per G e per n, quando n supera la dimensione di X. Ne segue in particolare che, ogniqualvolta si abbia una struttura fibrata di base X e gruppo G, G essendo un gruppo di Lie compatto, si ha un omomorfismo naturale dei gruppi di coomologia dello spazio classificante per G in quelli di X. Le immagini di certe classi di coomologia particolari nello spazio classificante sono elementi distinti nei gruppi di coomologia di X che sono caratteristici per la struttura fibrata scelta. Esse si chiamano ‛classi caratteristiche' e occupano un posto importante in varie applicazioni della topologia, in particolare a questioni di analisi e geometria differenziale. Per rendersi conto dei progressi compiuti da Borel e altri usando le successioni spettrali, consigliamo al lettore di leggere l'articolo di H. Samelson, Topology of Lie groups, pubblicato sul ‟Bulletin of the American Mathematical Society" nel 1952 e di leggere altresì l'articolo di Borel sullo stesso argomento pubblicato tre anni più tardi sulla medesima rivista.
La prima applicazione veramente incisiva delle successioni spettrali fu fatta da J. P. Serre in un lavoro del 1951 a cui abbiamo precedentemente accennato. Indichiamo con ΩX lo spazio, definito opportunamente, di tutti i ‛cammini' in un dato spazio topologico. Come già nel 1935 aveva osservato Hurewicz, il (j + 1)-esimo gruppo di omotopia πj+1(X) di X è isomorfo a πj(ΩX). D'altra parte ΩX si può considerare uno spazio fibrato (non una struttura fibrata) di base X. Applicando le successioni spettrali per collegare l'omologia di X a quella di ΩX e ricorrendo ad altri fatti che collegano i gruppi di omotopia di X all'omologia di ΩX, Serre riuscì a dedurre risultati sui gruppi di omotopia che prima di allora si erano mostrati assolutamente maccessibili. In particolare, egli riuscì a dimostrare che in molti casi questi gruppi possono essere calcolati esplicitamente con un procedimento sistematico in un numero finito di passi. La sfera Sn è un esempio di uno spazio topologico che, da molti punti di vista, ha una struttura particolarmente semplice. Tuttavia, prima delle ricerche di Serre, ben poco era noto sui gruppi di omotopia πj(Sn) per j > n, malgrado fossero stati compiuti molti sforzi in proposito. (Per j 〈 n, si dimostra facilmente che πj(Sn) è banale e che πn(Sn) è ciclico infinito come fu dimostrato da Hopf per tutti gli n > 0). Serre riuscì a dimostrare che, a meno di poche eccezioni, questi gruppi sono finiti e in molti casi riuscì a calcolarli esplicitamente.
Applicando le tecniche di Serre e altre introdotte da Eilenberg e MacLane, Postnikov, J. C. Moore, G. W. Whitehead e altri, all'inizio del 1950, si poterono computare i gruppi di omotopia dei gruppi di Lie compatti classici e dei loro spazi quozienti in numerosi casi speciali. Si osservi che Sn è omeomorfo allo spazio quoziente O(n + 1)/O(n). Fu tuttavia difficile ottenere risultati generali. Non esiste per esempio nessuna regola semplice generale per calcolare πj(Sn) quando siano dati n e j. Fu pertanto un evento sorprendente ed eccitante la scoperta, compiuta da R. Bott nel 1957, degli ormai famosi ‛teoremi di periodicità' per i gruppi di omotopia dei gruppi compatti classici. Indichiamo con K(n, F) il gruppo U(n), O(n) o Sp(n), a seconda che F = C, R o H (il corpo dei quaternioni). Applicando la successione esatta di omotopia citata dianzi, è possibile dimostrare, mediante ragionamenti elementari, che per ogni k e F, πk(K(n, F)) è isomorfo a πk(K(n + 1, F)) per ogni n sufficientemente grande. Ha senso pertanto parlare di
e questo gruppo è indicato con πk(U), πk(O), o πk(SP) a seconda che F = C, R o H. Il teorema di periodicità di Bott afferma che per tutti i k vale la relazione
πk(U) = πk+2(U)
πk(O) = πk+4(SP)
e
πk(SP) = πk+4(O).
Sulla base di queste e di un piccolo numero di determinazioni in casi particolari, si calcolano πk(U), πk(O) e πk(SP) per tutti i k, trovando in ogni caso l'identità, il gruppo ciclico infinito o il gruppo ciclico con due elementi.
Il teorema di periodicità si rivelò di notevole importanza non soltanto per il suo interesse intrinseco, ma anche per l'impatto che esso ebbe nel nuovo ramo della topologia, noto come K-teoria, al quale abbiamo accennato all'inizio di questo capitolo. Dato uno spazio topologico X, una ‛struttura fibrata complessa' su X è per definizione una struttura fibrata con base X le cui fibre sono spazi vettoriali complessi di dimensione finita e il cui gruppo è il gruppo GL(n, C) delle trasformazioni lineari non singolari in uno spazio vettoriale complesso di dimensione opportuna. Se V1 e V2 sono due strutture vettoriali complesse su X, per definizione la loro ‛somma diretta' V1 ⊕ V2 è l'insieme di tutte le coppie v1, v2 con v1 in V1 e v2 in V2 tali che v1 e v2 abbiano per immagine lo stesso punto di X. Questo insieme può essere visto come una struttura vettoriale complessa su X in un modo ovvio e naturale, in maniera che la fibra su x in X sia la somma diretta, come spazio vettoriale, delle fibre di V1 e V2 su x. Due strutture vettoriali complesse V1 e V2 si dicono ‛equivalenti' se esiste un omeomorfismo di V1 su V2 che, per ogni x in X, applica linearmente la fibra di V1 su x sulla fibra di V2 su x. Si verifica allora che V1′ ⊕ V2′ e V1 ⊕ V2 sono equivalenti ogniqualvolta V1′ è equivalente a V1′ e V2′ è equivalente a V2. Pertanto si può parlare senza timore di ambiguità di ‛somma diretta di classi di equivalenza di strutture vettoriali complesse su X'. Pensando a una classe di equivalenza di strutture vettoriali complesse come all'analogo di una classe di equivalenza delle rappresentazioni di un gruppo, si può definire un analogo del gruppo additivo di tutti i caratteri di dimensione finita di un gruppo e trasformarlo in un anello per mezzo di una nozione appropriata di prodotto tensoriale per strutture fibrate vettoriali complesse. Questo anello è un invariante topologico di X noto come K(X). Esso fu introdotto nel 1958 da Grothendieck nell'ambito della geometria algebrica e in relazione alle sue ricerche sulle generalizzazioni del classico teorema di Riemann-Roch. Tre anni più tardi Atiyah e Hirzebruch mostrarono come fosse possibile definire K(X) in un contesto topologico e sotto la guida di Atiyah la ‛K-teoria' è diventata uno strumento importante della topologia. Sotto molti aspetti, K(X) si comporta come la somma diretta dei gruppi di coomologia H0 ⊕ H1 ⊕ H2 ⊕ ..., che può anch'essa trasformarsi in un anello tutte le volte che il gruppo dei coefficienti sia esso stesso un anello. Tuttavia, K(X) ha alcuni vantaggi.
Una volta definito K(X), si pone il problema di determinarlo in casi concreti e, più in generale, di studiare le relazioni fra K(X), K(B) e K(F), quando X è uno spazio fibrato con base B e fibra F. Un lemma fondamentale afferma che K(X × S2) è isomorfo a K(X) ⊗ K(S2) quando ⊗ indichi un prodotto tensoriale di anelli opportunamente definito. Questo lemma risulta essere completamente equivalente all'affermazione πk(U) = πk+2(U) del teorema di periodicità di Bott. Anche le altre asserzioni del teorema di periodicità sono importanti per le K-teorie modificate, come per esempio quella che si occupa di strutture fibrate vettoriali reali.
Come abbiamo osservato precedentemente, il teorema che permette di ridurre lo studio della topologia dei gruppi di Lie a quello dei gruppi di Lie compatti non si applica agli spazi quozienti G/H. Tuttavia, come Montgomery dimostrò nel 1950, ogni spazio quoziente compatto G/H, in cui sia G che H sono gruppi di Lie connessi, è omeomorfo a uno spazio quoziente G′/H′ ove è un gruppo di Lie compatto connesso. Pertanto, i teoremi che richiedono un'indagine ulteriore sono quelli in cui G/H non è compatto e quelli in cui G/H è compatto ma G non è compatto e H non è connesso. Nel caso speciale in cui G è risolubile, lo spazio quoziente si chiama varietà risolubile e, nel caso ancora più particolare in cui G è nilpotente, lo spazio quoziente si chiama ‛nilvarietà'. La topologia di questi casi particolari è stata studiata in una serie di lavori a cominciare da quello fondamentale di Malcev sulle nilvarietà, del 1949, e quello sulle varietà risolubili, dovuto a Mostow, del 1954; questa serie di lavori è culminata in ricerche recentissime di L. Auslander e Toliemen. È noto che ogni nilvarietà è omeomorfa al prodotto fra Rk, per un k opportuno, e una nilvarietà compatta e che ogni nilvarietà compatta è omeomorfa a N/Γ, ove N è semplicemente connesso e nilpotente e Γ è isomorfo al gruppo fondamentale della varietà. Inoltre, due nilvarietà compatte sono omeomorfe se, e soltanto se, i loro gruppi fondamentali sono isomorfi e i gruppi fondamentali che compaiono sono proprio i gruppi nilpotenti finitamente generati privi di elementi di ordine finito. Per le varietà risolubili la situazione è più complessa. Una varietà risolubile non è necessariamente il prodotto di uno spazio compatto e di un Rk, ma è sempre una struttura fibrata vettoriale su una varietà risolubile compatta. Tuttavia due varietà risolubili compatte sono omeomorfe se, e soltanto se, i loro gruppi fondamentali sono isomorfi e si possono porre condizioni necessarie e sufficienti perché un gruppo discreto si presenti come un gruppo fondamentale siffatto. Esistono inoltre molti altri risultati più dettagliati. Le loro dimostrazioni, al pari di quelle dei risultati citati dianzi, dipendono, in una certa misura, dalla teoria dei gruppi lineari algebrici.
Gli spazi connessi G/H, quando G sia connesso e semi- semplice, hanno una struttura più complicata e non ancora ben chiara. Il caso particolare in cui H è un sottogruppo discreto e G/Γ è compatto o ha una misura invariante finita sorge in relazione alla teoria delle funzioni automorfe e a certe questioni di teoria dei numeri (v. in proposito i capp. 13 e 15). In tal caso si cercano condizioni su Γ perché G/Γ sia compatto e si cerca di ‛compattificare' G/Γ ‛aggiungendo' componenti di dimensione più bassa, quando G/Γ non sia già compatto.
13. Teoria dei gruppi e teoria dei numeri.
Il fine ultimo della teoria dei numeri è la risoluzione di sistemi di una o più equazioni polinomiali in un numero finito di incognite intere: la soluzione cioè di equazioni ‛diofantee'. La teoria dei numeri ha una storia lunga e complicata che risale a Euclide (300 a.C. circa) e a Diofanto (300 d.C. circa) e include importanti contributi di Fermat, nel XVII secolo, e di Eulero, nel XVIII. Tuttavia, fin verso la fine del XVIII secolo i risultati rimasero in gran parte frammentari e si riferivano a problemi particolari. Come anno di nascita della moderna teoria dei numeri possiamo assumere il 1773, anno in cui Lagrange pubblicò una memoria fondamentale nella quale veniva sistematizzata la teoria diofantea delle equazioni quadratiche in due incognite (ossia delle forme quadratiche binarie). Poiché il lavoro di Lagrange sulle permutazioni delle radici delle equazioni algebriche era apparso soltanto tre anni prima, si può ritenere che sia la teoria dei gruppi sia la teoria dei numeri moderna siano state create dallo stesso matematico quasi contemporaneamente. L'opera di Lagrange fu semplificata, e in certa misura estesa, da Legendre che nel 1798 pubblicò un libro su questo argomento. Tuttavia colui che fece per le idee di Lagrange sulla teoria dei numeri quello che Galois era riuscito a compiere per le idee dello stesso Lagrange sulla teoria dei gruppi fu C. F. Gauss, nato nel 1777. Di fatto Gauss riscoprì molti dei risultati di Lagrange e di Legendre prima di venire a contatto con l'opera di questi due scienziati. Le sue Disquisitiones arithmeticae pubblicate nel 1801 contengono i loro risultati, notevolmente estesi e migliorati, in quella che per molto tempo fu la loro forma finale. In particolare esse contengono la dimostrazione della famosa ‛legge di reciprocità quadratica'.
Consideriamo l'equazione diofantea x2 + y2 = n, ove n è un intero positivo dato. La forma quadratica x2 + y2 può essere fattorizzata come prodotto di x + iy e x − iy, ove i2 = - 1. D'altra parte, l'insieme di tutti i numeri x + iy, con x e y interi, è un anello che, rispetto alla fattorizzazione, si comporta come l'anello degli interi. Modulo unità (elementi dell'anello che hanno inversi rispetto alla moltiplicazione), ogni ‛intero gaussiano' x + iy può essere espresso in uno e un sol modo come prodotto di ‛interi gaussiani primi'. Si vede subito che le unità sono ± 1 e ± i. Inoltre, se p è un numero primo ordinario, si può dimostrare che x2 + y2 = p ha una soluzione in interi se, e soltanto se, p = 2 oppure p è un numero primo dispari della forma 4n + 1. Se p è un numero primo siffatto e x2 + y2 = p con x e y interi, x + iy e x − iy sono interi gaussiani primi il cui quoziente non è un'unità (a eccezione del caso in cui p = 2) e, modulo unità, ogni intero gaussiano primo è uno di questi oppure è un numero primo, ordinario del tipo 4n + 3. Una volta note le unità e i numeri gaussiani primi e sapendo come i numeri primi ordinari si fattorizzino in numeri gaussiani primi, non vi è difficoltà a trovare tutte le soluzioni dell'equazione diofantea x2 + y2 = n, per ogni intero positivo n. Si deve soltanto fattorizzare n in numeri ordinari primi, fattorizzare questi ultimi in numeri gaussiani primi e osservare che x + iy deve essere un'unità moltiplicata per il prodotto di un certo sottoinsieme di numeri gaussiani primi che compaiono nella fattorizzazione, preso in modo che il suo complemento coincida con il suo complesso coniugato. Più in generale, data una qualsiasi forma omogenea in due variabili A0xn + A1xn-1y + ... + Anyn, ove A0, A1, ..., An sono interi ordinari, è possibile scrivere tale forma come prodotto di fattori lineari A0(x − α1y)(x −α2y) ... x − αny), ove gli αj sono le radici dell'equazione polinomia A0αn + A1αn-1 + ... + An-1α + An = 0. Nella misura in cui il corpo generato dagli αj ammette un concetto di ‛intero' con associata una ‛legge di fattorizzazione unica', è possibile ridurre la soluzione delle equazioni diofantee della forma A0xn + A1xn-1y + ... + Anyn = m alla decomposizione di m in ‛fattori primi'. Nel 1849, Kummer cercò di applicare questo metodo alla famosa equazione di Fermat xp + yp = zp fattorizzando xp + yp in (x + y)(x + αy) • (x + α2y) ... (x + αp-1y), ove α = e2πi/p e p è un numero primo dispari. Egli tuttavia commise l'errore di supporre tacitamente che i suoi ‛interi', i numeri della forma n1 + n2α + ... + npαp-1 (essendo gli nj interi ordinari), fossero simili a quelli gaussiani nell'obbedire a una legge di fattorizzazione unica. Di fatto essi si comportano in tal modo soltanto per alcuni valori del numero primo p. Questo errore fu all'origine di uno studio dettagliato degli anelli degli ‛interi algebrici' intrapreso da Kummer e da altri, che, all'inizio del 1870, culminò nella teoria di Dedekind degli ‛ideali' nei corpi di numeri algebrici. Gran parte della teoria delle forme quadratiche binarie, così come era stata sviluppata da Lagrange, Legendre e Gauss, insieme con importanti contributi apportati intorno al 1830 da Dirichlet, allievo di Gauss, può essere riformulata nel linguaggio della teoria dei numeri algebrici e non è altro che un caso particolare di questa teoria quando il corpo dei numeri è ‛una estensione quadratica dei numeri razionali'. Alcune di queste nozioni inoltre sono più facilmente comprensibili e descrivibili usando tale linguaggio. Sarà pertanto opportuno abbandonare la successione cronologica e tratteggiare la teoria di Dedekind prima di addentrarci in ulteriori dettagli sui contributi di Lagrange, Gauss e Dirichlet.
Per definizione, un ‛numero algebrico e un numero complesso che soddisfa l'equazione polinomia a0 + a1x + a2x2 + ... + anxn = 0, ove an ≠ 0 e a0, a1, ..., an sono tutti interi. Se si possono scegliere gli aji in modo tale che an = 1 si dice che il numero algebrico è un ‛intero algebrico'. L'insieme di tutti i numeri algebrici è un sottocorpo del corpo dei numeri complessi e l'insieme di tutti gli interi algebrici è un sottoanello di questo corpo. Un sottocorpo del corpo di tutti i numeri algebrici prende il nome di ‛corpo di numeri algebrici'. Un corpo di numeri algebrici generato da un numero finito di suoi elementi è sempre generato da uno di essi e questo generatore ϑ può essere scelto in modo che esso sia un intero algebrico e soddisfi l'equazione ϑn + an-1ϑn-1 + ... + a1ϑ + a0 = 0, ove gli aj sono interi ordinari e il polinomio xn + an-1xn-1 + ... + a1x + a0 è ‛irriducibile', nel senso che non può essere fattorizzato come prodotto di due polinomi a coefficienti interi e di ordini minori. Questo corpo si indica con Q(ϑ) ove Q denota il corpo dei numeri razionali. Per ovvie ragioni, corpi di questo tipo vengono chiamati estensioni finite di Q. Gli interi algebrici in Q(ϑ) formano un anello e si può dimostrare che questo anello contiene n elementi β1, β2, ..., βn tali che ogni intero algebrico può essere espresso, in uno e un solo modo, nella forma m1β1 + ... + mnβn, ove gli mj sono interi ordinari. L'intero n è pertanto indipendente dalla scelta di ϑ in Q(ϑ) e viene chiamato ‛grado' dell'estensione. Si può dimostrare che ogni elemento di Q(ϑ) è il quoziente di un intero algebrico per un intero ordinario e che pertanto ogni elemento di Q(ϑ) si può esprimere in uno e un solo modo come combinazione lineare razionale dei βj. Dedekind aggirò la dificoltà dovuta alla mancanza di una legge di fattorizzazione unica spostando l'attenzione dagli interi algebrici agli ‛ideali' da questi generati. Un ‛ideale' in un qualsiasi anello commutativo è un sottogruppo del gruppo additivo che contiene ab ogniqualvolta a appartiene all'ideale e b sta nell'anello. In particolare, l'insieme di tutti gli xy con x fissato e y arbitrario è un ideale che prende il nome di ‛ideale principale' generato da x. Nel nostro caso si vede facilmente che x1 e x2 generano lo stesso ideale principale se, e soltanto se, x1 = wx2, ove w e un unità. Se ℛ è l'anello di tutti gli interi algebrici in un Q(ϑ) e se ϑ è tale che ℛ ammetta una legge di fattorizzazione unica, ogni ideale è principale e la legge di fattorizzazione unica può essere espressa mediante ideali in questo modo: definiamo il prodotto I1 • I2 di due ideali come l'insieme di tutti gli elementi a1b1 + a2b2 + ... + anbn, ove gli aj stanno in I1 e i bj in I2. Ogni ideale in ℛ diverso da 0 e da ℛ può essere scritto in uno e in un sol modo nella forma I1k1I2k2...Irkr, ove i kj sono interi positivi e gli Ij sono ideali distinti ‛primi', nel senso che non possono essere ulteriormente fattorizzati. Il grande vantaggio di questa nuova forma di enunciato è che il teorema risultante vale per l'anello degli interi algebrici in un qualsiasi Q(ϑ). Se si considerano gli ideali non principali, la fattorizzazione unica vale senza eccezioni. Data un'equazione diofantea, A0xn + A1xn-1y + ... + Anyn = m, la fattorizzazione A0 • (x − α1y)...(x − αny) del primo membro può essere riscritta nella forma (1/B)(β1x − γ1y)(β2x − γ2y)...(βnx − γny), ove i γj sono interi algebrici in un corpo Q(ϑ), mentre B e βj sono interi ordinari. Pertanto l'equazione diventa (β1x − γ1y)(β2x − γ2y)...(βnx − γny) = Bm che, (modulo unità) vale se, e soltanto se, I1I2...In = ℛBm, ove Ij è l'ideale principale generato da βjx − γjy e ℛBm quello generato da Bm. Per trovare la soluzione più generale dell'equazione modulo unità, basta fattorizzare ℛBm in ideali primi e considerare il modo di suddividerli in n sottoinsiemi. Non ogni divisione dà luogo tuttavia a una soluzione. Bisogna aggiungere due ulteriori condizioni. Una di queste è analoga alla condizione, nel caso gaussiano, secondo cui il complesso coniugato di ogni elemento in un sottoinsieme deve appartenere all'altro. Essa afferma che ogni automorfismo (isomorfismo su se stesso) di Q(ϑ) deve trasformare ciascuno degli n sottoinsiemi su se stesso o su un altro di tali sottoinsiemi. La seconda condizione, superflua quando ogni ideale è principale, afferma che il prodotto degli ideali primi in ciascuno degli n sottoinsiemi deve essere un ideale principale. Nel caso delle forme quadratiche con n = 2, Q(ϑ) ammette uno e un solo automorfismo non banale e non vi sono difficoltà ad applicare la prima condizione. Per applicare la seconda, tuttavia, è necessario sapere, per ogni insieme finito di ideali primi, se il prodotto dei suoi elementi è, oppure no, principale. Ottenere questa informazione è un problema molto meno arduo di quanto non sembri, in virtù delle proprietà di una certa relazione di equivalenza fra ideali. Si dice che gli ideali I1 e I2 (siano essi primi oppure no) stanno nella stessa ‛classe' se esistono degli ideali principali J1 e J2 tali che I1J1 = I2J2. È ovvio che la classe del prodotto di due ideali dipende soltanto dalle classi dei fattori, cosicché si può parlare, senza timore di malintesi, del prodotto di due classi. È infine possibile dimostrare l'importante teorema secondo il quale esiste soltanto un numero finito di classi ed esse formano un gruppo commutativo per l'operazione di prodotto testé definita. Questo gruppo prende il nome di ‛gruppo delle classi di ideali' (o, brevemente, ‛gruppo delle classi', o anche ‛gruppo di classe') del corpo Q(ϑ) e il suo ordine si chiama ‛numero delle classi o numero di classe'. Evidentemente un dato prodotto di ideali primi è principale se, e soltanto se, il prodotto delle classi corrispondenti è l'identità nel gruppo delle classi di ideali. Pertanto, per sapere quali prodotti di ideali primi sono principali basta conoscere la struttura del gruppo di classi di ideali e a quale elemento di esso appartiene ogni ideale primo.
Il gruppo delle classi di ideali per un'estensione di secondo grado dei numeri razionali fu introdotto da Gauss nelle sue Disquisitiones con il linguaggio delle forme quadratiche. Si definiscono come equivalenti due forme quadratiche Ax2 + Bxy + Cy2 e A′x2 + B′xy + C′y2 se la prima di esse è trasformata nella seconda da una sostituzione della forma x ???14??? ax+by, y ???14??? cx + dy, ove ad − bc = 1 e a, c e d sono interi. Chiamando B2 − 4AC il ‛discriminante' di Ax2 + Bxy + Cy2, si vede che forme equivalenti hanno lo stesso discriminante. Gauss inventò una formula complicata per ‛comporre' due forme con discriminante D, in modo da ottenere un'altra forma con lo stesso discriminante. Questa legge di composizione ne definisce un'altra per la composizione delle classi di equivalenza e l'insieme delle classi di equivalenza è un gruppo commutativo finito rispetto alla composizione di forme quadratiche con uguale discriminante. Esiste una corrispondenza naturale fra gli ideali in Q(√-D) e le forme quadratiche di discriminante D, la quale stabilisce un isomorfismo tra il gruppo definito da Gauss e il gruppo delle classi di ideali in Q(√-D). Naturalmente Gauss non usò la nomenclatura della teoria dei gruppi (che a quei tempi non esisteva), ma fu nel contesto di quest'ultima che egli dimostrò i teoremi fondamentali di struttura per i gruppi finiti commutativi e introdusse per la prima volta la nozione di carattere (a una dimensione) di un gruppo (v. sopra, capp. 1 e 4).
Per ogni corpo Q(ϑ), estensione finita del corpo dei razionali, si pongono i seguenti problemi: 1) trovare gli ideali primi di Z(ϑ) per ogni primo ordinario p, trovare la fattorizzazione dell'ideale primo generato da p mediante gli ideali primi di Z(ϑ). (Di solito questa viene semplicemente chiamata fattorizzazione di p); 3) trovare la struttura del gruppo delle classi di ideali e l'immagine in esso di ogni ideale primo di Z(ϑ); 4) trovare il gruppo moltiplicativo delle unità in Z(ϑ); 5) trovare il gruppo G(ϑ) degli automorfismi di Q(ϑ) e la sua azione sugli ideali primi di Z(ϑ). Il caso più semplice è naturalmente quello in cui il grado di Q(ϑ) è 2; le risposte possibili in tal caso sono in gran parte riformulazioni dei risultati principali della teoria classica delle forme quadratiche binarie. In questo caso naturalmente il gruppo degli automorfismi di Q(ϑ) ha ordine 2 e può essere esaminato senza ricorrere alla teoria dei gruppi come tale. Nel caso generale si tratta del famoso gruppo di Galois sul quale Galois basò le sue profonde ricerche sulla risolubilità delle equazioni nel 1831, trent'anni dopo la pubblicazione delle Disquisitiones di Gauss. L'estensione Q(ϑ) si chiama ‛estensione di Galois' se per ogni ϕ in Q(ϑ), non razionale, esiste un α in G(ϑ) tale che α(ϕ) ≠ ϕ. Il corpo generato dai razionali e dalle radici di un equazione polinomia con coefficenti razionali è sempre un estensione di Galois e lo è anche l'estensione che compare nello studio di A0xn + A1xn-1y + ... + Anyn = m mediante la fattorizzazione. Pertanto il caso di Galois è il più interessante. Ovviamente un'estensione di secondo grado è sempre un'estensione di Galois. I problemi 1), 2) e parte del problema 5) sono strettamente legati, in quanto si può dimostrare che ogni ideale primo in Z(ϑ) appare come un fattore nella decomposizione di uno e un solo numero primo ordinario p; è ovvio inoltre che il gruppo di Galois G(ϑ) permuta tra loro gli ideali fattori primi di un p dato. Inoltre, quando Q(ϑ) è un'estensione di Galois, si dimostra facilmente che l'azione di G(ϑ) sugli ideali fattori primi di un dato p è transitiva. Pertanto (nel caso di Galois) ogni numero primo ordinario p si decompone in un certo numero di ideali primi che sono tutti simili tra loro, nel senso che essi possono essere trasformati l'uno nell'altro da automorfismi di Z(ϑ), e non c'è molto da dire su di essi una volta indicati il loro numero e la loro molteplicità. È possibile dare simultaneamente ai problemi 1) e 2) una ‛soluzione', in un certo senso, assegnando le due funzioni che a ogni numero primo ordinario p fanno corrispondere il numero degli ideali primi distinti nel quale esso si decompone e la molteplicità (comune) con la quale essi si presentano. La seconda funzione risulta essere la stessa per tutti i numeri primi, a eccezione di un numero finito di essi - cosiddetti numeri primi ramificati. La più difficile da descrivere è dunque la prima funzione. Identificando due elementi di Z(ϑ) tutte le volte che la loro differenza appartiene a un ideale I, le operazioni in Z(ϑ) definiscono operazioni corrispondenti nell'insieme Z(ϑ)/I di tutte le classi di equivalenza e fanno di Z(ϑ)/I un anello che viene chiamato anello delle classi residue. Esso consta sempre di un numero finito di elementi e tale numero prende il nome di norma N(I) dell'ideale I. Si può dimostrare che N(I1I2) = N(I1) • N(I2) e che Z(ϑ)/I è un corpo se, e soltanto se, I è un ideale primo. Inoltre, quando I è l'ideale principale generato da un intero ordinario m, N(I) = mn, ove n è il grado dell'estensione del corpo. Ne segue che, se p si decompone in g ideali primi, ciascuno di norma Np e molteplicità l, risulta (Ngpl) = pn, cosicché Np = pf, ove f = n/gl. Pertanto g e l dividono ambedue n e si può descrivere la decomposizione di un numero primo p non ramificato, assegnando g oppure f = n/g. In particolare, poiché n ha soltanto un numero finito di divisori, esiste soltanto un numero finito di tipi diversi di numeri primi ordinari rispetto alla fattorizzazione in Q(ϑ) e il problema consiste nel determinare delle regole che prescrivano a quale classe ciascun p appartiene.
Quando n = 2, ci sono soltanto due tipi di numeri primi non ramificati: quelli che si fattorizzano in due ideali primi distinti di norma p e quelli che generano un ideale primo semplice di norma p2. Inoltre ogni numero primo ramificato genera un ideale principale che è il quadrato dell'ideale primo di norma p. Vi è anche un semplice criterio per decidere a quale di queste tre classi appartiene un numero primo ordinario p. Si ha sempre Q(ϑ) = Q(√-D), ove D è un intero privo di quadrati, e si può dimostrare che i numeri primi dispari che sono ramificati sono precisamente quelli che dividono D. Un numero primo dispari p che non divide D si fattorizza in uno o due ideali primi a seconda che D sia o non sia un quadrato nel corpo dei p elementi. Il numero primo 2 si comporta in modo del tutto diverso: esso è non ramificato se e soltanto se D è della forma 4n + 1, ove n è un intero, e si fattorizza in due ideali primi distinti se, e soltanto se, D è della forma 8n + 1. Pur essendo completo, questo risultato non è esauriente per la seguente ragione: il modo in cui p si fattorizza in Q(√-D) è una funzione di due variabili, p e D, ed è stata presentata come una semplice funzione di D definita per ciascun valore di p. Sarebbe molto più utile per noi averla come una semplice funzione di p definita per ogni valore di D. Naturalmente ciascuna delle due presentazioni determina univocamente l'altra. Non è tuttavia affatto chiaro se le funzioni di p, definite considerando proprietà di D mod p, possano essere calcolate a partire da p mediante una formula semplice. Il fatto che ciò accada è il contenuto della famosa legge di reciprocità quadratica alla quale abbiamo accennato precedentemente. Dati due numeri primi p e q, la legge permette di decidere se p è un quadrato nel corpo di q elementi non appena sia noto se q è, oppure no, un quadrato nel corpo di p elementi. In forma compatta, essa afferma che
ove (p/q) è il cosiddetto ‛simbolo di Legendre' uguale a 1 o −1 a seconda che p sia, oppure no, un quadrato nel corpo di q elementi. In base a questa legge e a due ‛complementi' relativi al caso 2 e −1,
si può esprimere (D/q) per ogni numero primo q e ogni intero D in funzione del comportamento di q nell'anello degli interi mod 4D. Se χ è la funzione che vale zero sui numeri primi ramificati e 1 o −1 su quelli non ramificati, a seconda che essi si fattorizzino rispettivamente in due o in un ideale primo in Q(√-D), e χ(p1n1p2n2...prnr) è presa per definizione uguale a χ(p1)n1χ(p2)n2...χ(pr)nr, allora la legge di periodicità quadratica implica che χ è periodica con periodo 4D. La funzione definita sui numeri primi e a valori 0, 1 e −1, che definisce la loro legge di decomposizione, non è altro che la restrizione ai numeri primi di una funzione elementare definita sugli interi positivi, che può essere data esplicitamente.
Pur disponendo della legge di decomposizione riformulata mediante la reciprocità quadratica, vi è una semplice questione relativa a essa, la cui risposta non è banale. Sappiamo che tutti i numeri primi sono non ramificati a eccezione di un numero finito di essi e che quelli non ramificati si dividono in due classi a seconda che χ(p) = ± 1. È tuttavia lecito pensare che una di queste due classi sia finita o persino vuota e per un certo tempo la congettura che ambedue le classi fossero infinite rimase aperta. Dalla nuova formulazione della legge di decomposizione si capisce che questa congettura è conseguenza dell'altra, secondo cui vi è una famiglia finita di numeri primi in ogni progressione aritmetica i cui termini non abbiano fattori comuni. Questa congettura fu dimostrata da L. P. J. Dirichlet, nel periodo che va dal 1837 al 1840, facendo un uso sistematico di strumenti analitici e in particolare di serie infinite della forma
con s variabile reale, e della nozione di ‛densità' di un insieme infinito di interi. Questi strumenti si rivelarono utili in un campo esteso di problemi di teoria dei numeri e le serie della forma indicata (al pari di certe loro generalizzazioni) vanno ora sotto il nome di serie di Dirichlet. Dirichlet passò gran parte della sua carriera analizzando e semplificando l'opera di Gauss. A lui si attribuisce il merito di essere stato il primo ad averla approfondita. La sua Zahlentheorie, che apparve in edizioni successive nel 1863, 1871, 1879 e 1893, rese l'opera di Gauss accessibile a un pubblico molto più vasto. Dirichlet ottenne la sua dimostrazione come corollario di un risultato più forte, secondo cui i numeri primi che appartengono a una progressione aritmetica (e i cui termini non hanno fattori in comune) sono tali che la somma dei loro inversi diverge. Eulero aveva dimostrato il fatto corrispondente per tutti i numeri primi servendosi della sua famosa formula del prodotto per le serie
ove il prodotto si estende a tutti i numeri primi p ed entrambi i membri convergono per s > 1. Dirichlet osservò che esiste una formula del prodotto simile per
ove χ è una funzione a valori complessi definita sugli interi positivi, che è ‛moltiplicativa', nel senso che χ(n1n2) = χ(n1)χ(n2), e tale che ∣ χ(n) ∣ ≤ 1. Dato un intero positivo m, quelle funzioni moltiplicative χ che sono periodiche con periodo m e sono zero per gli interi aventi fattori in comune con m, corrispondono in modo biunivoco ai caratteri a una dimensione del gruppo degli elementi invertibili nell'anello degli interi mod m. Tali funzioni χ si chiamano ‛caratteri di Dirichlet' mod m e le corrispondenti funzioni s ???14??? L(s, χ) prendono il nome di L-serie di Dirichlet o funzioni L o L-funzioni. Se m è un numero primo, vi sono esattamente m − 1 caratteri mod m. Si vede (mediante l'analisi di Fourier o la teoria dei gruppi abeliani finiti) che ogni funzione a valori complessi sugli interi, che si annulla su m ed è periodica di periodo m, è una combinazione lineare finita di tali caratteri. Basandosi su questi fatti, Dirichlet riusci a generalizzare la dimostrazione di Eulero, purché fosse possibile dimostrare che L(1, χ) = lims→1 L(s, χ) ha un valore finito non nullo ogniqualvolta χ è un carattere di Dirichlet mod m diverso dal carattere banale. Questo risultato può ottenersi direttamente eccetto quando x è di ordine 2 (o, equivalentemente, ha valore reale). Per trattare questo caso, Dirichlet legò L(s, χ) a una serie di Dirichlet del tipo
ove F(n) è il numero degli ideali di norma n in Q(√-D) e D dipende da χ. (Naturalmente Dirichlet pensava in termini di forme quadratiche e F(n) era definita in modo un po' diverso).
Si osservi che
ove I varia nella famiglia di tutti gli ideali di Z(√-D) distinti da zero e quindi è una diretta generalizzazione della
Essa viene chiamata la funzione ‛zeta' del corpo Q(√-D). Per la ζ vale la formula del prodotto di Eulero
ove p varia fra tutti gli ideali primi. Raggruppando gli ideali primi associati a ogni numero primo ordinario p, si vede che ciascun p porta al prodotto un contributo uguale a
a seconda di come p si decompone. Poiché
questo contributo apportato da p può essere scritto in tutti e tre i casi nella forma
ove χ′(p) = 1, −1, o 0. Pertanto
Ma χ′ è un carattere di Dirichiet e, mediante un'opportuna scelta di D, esso può farsi coincidere con χ, cosicché
Per completare la dimostrazione, Dirichlet si servì di un'argomentazione geometrica diretta per dimostrare che i numeri N(I) hanno una densita finita e non nulla l, cioè che
esiste ed è finito e positivo. Ora, in base a un semplice teorema dell'analisi,
ogniqualvolta ϕ è positiva e il limite al secondo membro esiste. Ne segue che
e n non può annullarsi. L'argomentazione che condusse Dirichlet all'esistenza di l prova di fatto qualcosa di più e precisamente che
esiste ed è finito, positivo e indipendente da α; Fα(n) è il numero di ideali di norma n che appartengono alla classe di ideali α. Poiché Dirichlet aveva anche ottenuto una formula esplicita per l′ in funzione di D e poiché l = h(D)l′, ove h(D) è il numero di classe di Q(√-D), egli poté concludere che h(D) = L(1, χ)/l′ e ottenere così una formula per il numero di classe mediante la legge di decomposizione dei numeri primi.
Si osservi che la formula ζK(s) = ζ(s)L(s, χ), ove ζK è la funzione zeta del corpo K = Q(√-D) e χ il carattere di Dirichlet appropriato, è equivalente alla legge dei fattori primi in K. Molti fatti importanti della teoria dei numeri si possono così esprimere concisamente e in modo conveniente mediante identità che involgono serie di Dirichlet. L'importanza di queste ultime sta anche nella loro utilità nel dimostrare teoremi sui numeri primi. Dato un K = Q(√-D), si consideri la funzione FKα(n) che conta il numero degli ideali di norma n nella classe di ideali α. Si può costruire
la funzione zeta della classe α, ma, a meno che
non vi è fattorizzazione sui primi. Tuttavia, per ogni carattere del gruppo delle classi di ideali si può definire la ‛L-funzione'
ove la prima sommatoria è estesa a tutti gli ideali propri e Ī è la classe alla quale appartiene I. Poiché -χ- (-I-1-I-2) = χ(Ī1)χ(I2), ne segue, come nel caso della funzione zeta, che
ove il prodotto è esteso a tutti gli ideali primi p. Inoltre, i metodi dell'analisi di Fourier finita mostrano che
Dunque, conoscere LK equivale a conoscere la χ(p), il che a sua volta equivale a sapere come gli ideali primi sono distribuiti fra le classi. D'altra parte la conoscenza di LK equivale, in base all'analisi di Fourier finita, a conoscere la ζKα e quindi le FKα.
Considerando l'insieme dei coefficienti a1, a2, ... come una funzione definita sul gruppo dei numeri razionali positivi, la quale è nulla eccetto che sugli interi, e ricordando che (r1r2)s = rs1rs1, si può interpretare
come una specie di trasformata di Fourier di n ???14??? an, in cui gli omomorfismi nei numeri reali positivi prendono il posto di quelli nei numeri complessi di modulo 1. Si ottengono caratteri ordinari quando s è puramente immaginario, ma
non converge per moltissime successioni di interesse nella teoria dei numeri. D'altra parte, si possono far assumere a s valori complessi e considerare
come il prolungamento analitico naturale della somma non definita
Quando {∣ an ∣} non è illimitata troppo irragionevolmente,
converge per tutti gli s la cui parte reale sia sufficientemente grande e definisce una funzione analitica di s. Se questa funzione analitica può essere prolungata all'asse dei numeri immaginari puri (e ciò accade spesso) si può attribuire un significato alla
Il primo a occuparsi seriamente delle serie di Dirichlet come di funzioni nel piano complesso fu Riemann. In un breve lavoro, pubblicato nel 1859 e rivelatosi di estrema importanza per gli sviluppi successivi, egli mostrò che la classica funzione zeta
non soltanto può essere prolungata analiticamente in tutto il piano complesso a eccezione di un polo nel punto s = 1, ma che esiste una equazione funzionale semplice che lega i suoi valori nel semipiano alla destra della retta σ = 1/2 ai suoi valori nel semipiano alla sinistra della stessa retta (s = σ + iτ). Questa equazione funzionale è
ove
Da essa si deduce facilmente che ζ(−2n) = 0 per n = 1, 2, 3, ... e che ζ non si annulla che all'interno della ‛striscia critica' 0 ≤ σ ≤ 1. Per σ > 1, la convergenza del prodotto di Eulero assicura l'assenza di zeri. Funzioni di una variabile complessa che hanno soltanto singolarità polari e che non crescono ‛troppo rapidamente' all'infinito sono quasi univocamente determinate dai loro zeri e dai loro poli e possono essere espresse come prodotti infiniti convergenti dappertutto, che mettono in evidenza i loro zeri e i loro poli. In base a ciò e alla formula
valida per σ > 1, ci si aspetta una stretta relazione fra i numeri primi p e gli zeri di ζ. In quest'ordine di problemi, Riemann enunciò una serie di congetture sulla ζ e sui suoi zeri, alcune delle quali vennero dimostrate, intorno al 1890, da Hadamard e da von Mangolt. Le congetture effettivamente dimostrate ebbero un ruolo importante nella dimostrazione del famoso teorema dei numeri primi, secondo il quale se π(x) è il numero dei numeri primi ≤ x, risulta limx→∞ π(x) log x/x = 1. Questo risultato fu ottenuto da Hadamard e de la Vallée Poussin nel 1896. La più famosa fra le congetture di Riemann afferma che tutti gli zeri sulla striscia critica stanno di fatto sulla retta σ = 1/2. La validità di questa congettura avrebbe una serie di implicazioni sugli aspetti più dettagliati della distribuzione dei numeri primi. Essa tuttavia non è stata ancora dimostrata dopo più di un secolo dalla sua formulazione.
Seguendo le orme di Riemann, molto è stato fatto relativamente al prolungamento analitico e alle equazioni funzionali per le altre serie di Dirichlet che si presentano nella teoria dei numeri. Di queste parleremo fra breve. In ogni caso un passo decisivo nella dimostrazione dell'equazione funzionale è l'applicazione di un'identità che appartiene all'analisi classica di Fourier e che viene chiamata formula sommatoria di Poisson. Nella sua forma classica più semplice, essa afferma che, per un'opportuna scelta della funzione regolare f di una variabile reale, si ha
ove
Quest'identità ha un'ovvia generalizzazione al caso di funzioni di più variabili, che, a sua volta, è un caso particolare del seguente teorema sui gruppi abeliani G localmente compatti e separabili. Sia H un sottogruppo chiuso di G e sia H- l'annullatore di H nel gruppo duale G. È allora possibile scegliere le misure di Haar in G, Ø, H e H⊥ in modo tale che, per tutte le f regolari in un senso opportuno, si abbia
ove
Fino a che si considerano soltanto forme quadratiche, con Q(ϑ) di secondo grado, i soli gruppi che si presentano sono commutativi (il gruppo delle classi di ideali, il gruppo delle unità negli interi mod m, ecc.) e la tecnica della teoria dei gruppi alla quale si ricorre è essenzialmente l'analisi di Fourier (commutativa). Tuttavia, passando alle forme binarie e a estensioni di grado più alto, il gruppo degli automorfismi di Q(ϑ) (il suo gruppo di Galois) diventa molto meno banale (in particolare non è necessariamente commutativo) e sostiene un ruolo molto più importante nella teoria. I risultati fondamentali di Galois sulla risolubilità delle equazioni (teoria di Galois) hanno una posizione centrale e in questo contesto possono essere formulati nel modo seguente. Sia K = Q(ϑ) un corpo, estensione finita di Galois dei razionali, e sia GK il gruppo di tutti gli automorfismi di K. Per ogni sottogruppo H di GK, sia KH l'insieme di tutti gli x in K tale che h(x) = x per tutte le h in H. GK risulta finito, KH è un sottocorpo di K e l'applicazione H ???14??? KH è una bigezione dall'insieme di tutti i sottogruppi di GK sull'insieme di tutti i sottocorpi di K. Inoltre, il corpo KH è un'estensione di Galois di Q se, e soltanto se, H è un sottogruppo normale di GK. Quando lo è, il gruppo quoziente G/H è canonicamente isomorfo al gruppo di tutti gli automorfismi di KH.
Come è lecito aspettarsi, la difficoltà del problema di trovare gli ideali primi in K0 = Z(ϑ) è strettamente legata alla struttura del gruppo di Galois; essa è meno ardua quando questo gruppo è non soltanto commutativo, ma ciclico di ordine primo. Più in generale, ogniqualvolta il gruppo di Galois ammette un sottogruppo normale proprio N, si può dividere il problema in due sottoproblemi più facili, introducendo il corpo KN, estensione intermedia di Galois. Si cercano anzitutto gli ideali primi nell'anello degli interi di KN e successivamente si esamina in qual modo ciascuno di questi ideali primi si fattorizza nell'anello, più grande, di tutti gli interi in K. Naturalmente si può usare questo procedimento soltanto dopo aver generalizzato la teoria delle estensioni, che abbiamo dianzi descritto, in una teoria di ‛estensioni relative' in cui Q è sostituito da Q(ϑ) e i numeri primi ordinari sono sostituiti da ideali primi nell'anello Z(ϑ) di tutti gli interi in Q(ϑ). Tuttavia, questa generalizzazione può essere realizzata in modo relativamente diretto, sebbene l'analogo di un carattere di Dirichlet mod m è notevolmente più complicato da definire quando ϑ ≠ 1. Il problema chiave consiste allora nel trovare come gli ideali primi in Z(ϑ) si decompongono in un corpo che sia un'estensione più ampia e il cui gruppo di Galois (relativo) non abbia sottogruppi normali. Un G siffatto, naturalmente, sarà non commutativo oppure ciclico di primo ordine. Mentre sul primo caso si conosce ben poco, il secondo è stato assiduamente studiato ed esistono ormai risultati più o meno completi. Questi, particolarizzati al caso in cui Z(ϑ) = Z e il gruppo di Galois ha ordine 2, includono non soltanto il teorema relativamente superficiale che collega la decomposizione di un numero primo fissato p al comportamento di D, ma anche la legge di reciprocità quadratica e il suo corollario sulla fattorizzazione della funzione zeta del corpo come prodotto della funzione zeta dei numeri razionali e di una L-funzione di Dirichlet. Essi includono infine un teorema, che dianzi non abbiamo enunciato, il quale indica quali L-funzioni di Dirichlet si presentano e pertanto stabilisce una corrispondenza biunivoca fra tutte le estensioni quadratiche dei numeri razionali e una classe ben definita di caratteri di Dirichlet. Stabilire questi risultati non fu cosa facile. Essi vennero gradualmente ottenuti, nell'arco di parecchi decenni, grazie agli sforzi congiunti di Kummer, Weber, Hilbert, Furtwangler e Takagi. Sarebbe troppo complicato dare qui i dettagli di tutta la storia. Basti dire che i tratti essenziali furono dati da Hilbert all'inizio di questo secolo dopo che egli aveva studiato l'opera precedente di Kummer e Weber. Molte delle sue congetture non dimostrate furono provate da Furtwangler nel decennio successivo e Takagi diede una trattazione più o meno completa del caso generale intorno al 1920. Un miglioramento importante venne apportato da Artin nel 1927 e l'esposizione può essere notevolmente semplificata facendo ricorso all'opera di quest'ultimo e alla nozione di gruppo delle classi di idèle o ‛gruppo idèle' introdotta da Chevalley nel 1933.
Nella formulazione della teoria precedente al 1933, l'analogo di un carattere di Dirichlet è un carattere definito su un gruppo abeliano finito il quale generalizza il gruppo delle classi di ideali ed è chiamato un ‛gruppo di classi di divisori di congruenza'. Il ‛gruppo di classi di idèle' di un corpo di numeri algebrici è un gruppo abeliano localmente compatto infinito separabile, il quale non è nè discreto nè separabile e i cui gruppi quozienti di ordine finito sono esattamente i gruppi di classi di divisori di congruenza. Identificando due caratteri di Dirichlet quando essi coincidono sul loro dominio comune, si ha una corrispondenza biunivoca naturale fra i caratteri di Dirichlet così identificati e i caratteri a una dimensione di ordine finito del gruppo di classi di idèle del corpo dei numeri razionali. In generale, per un corpo di numeri algebrici, si definisce carattere di Dirichlet un carattere di ordine finito di un gruppo di classi di idèle. Poiché il gruppo delle classi di ideali è uno speciale gruppo di classi di divisori di congruenza, i caratteri del gruppo delle classi di ideali sono inclusi come caso particolare. In corrispondenza a ognuno di questi caratteri generalizzati di Dirichlet, si ha una funzione L di cui daremo ora la definizione. Un risultato centrale della teoria è che, per ogni corpo di numeri algebrici K, esiste una corrispondenza naturale biunivoca fra i gruppi quozienti di ordine finito del gruppo di classi di idèle e le sue estensioni finite di Galois K(ϑ) aventi un gruppo di Galois G(ϑ) abeliano. Inoltre, in questa corrispondenza, il gruppo di Galois e il gruppo quoziente sono isomorfi. Esattamente come nel caso quadratico, la legge di decomposizione degli ideali primi può essere espressa dicendo che la funzione zeta del corpo estensione di K può essere fattorizzata in un certo modo. Qui i fattori sono le funzioni L associate ai caratteri del corrispondente gruppo quoziente del gruppo delle classi di idèle. Il fatto che esista un'applicazione canonica del gruppo delle classi di idèle sul gruppo delle classi di ideali distingue un gruppo quoziente di ordine finito del primo e quindi un particolare corpo estensione di K. Questo corpo prende il nome di ‛corpo delle classi di Hilbert di K′. Esso può essere caratterizzato come l'estensione di Galois massimale di K avente un gruppo di Galois commutativo e che è non ‛ramificata' nel senso che è dotata delle seguenti due proprietà: a) ogni ideale primo nell'anello degli interi di K si decompone in ideali primi distinti nell'estensione; b) una proprietà analoga per i cosiddetti ‛primi all'∞', cioè le immersioni dense di K nei corpi dei numeri reali e complessi. (Spiegheremo più avanti la relazione fra primi e immersioni dense). Hilbert e Furtwangler si occuparono principalmente delle estensioni non ramificate e del corpo delle classi di Hilbert. Takagi ampliò l'estensione al caso ramificato.
Il grande contributo di Artin consistette nel provare che l'isomorfismo fra il gruppo di Galois e il gruppo delle classi di divisori di congruenza associato poteva essere definito in modo canonico mediante un'applicazione dagli ideali primi al gruppo di Galois introdotto da Frobenius nel 1896. Come abbiamo osservato dianzi, ogniqualvolta un numero primo ordinario è non ramificato in un corpo Q(ϑ), estensione di Galois, il gruppo di Galois G(ϑ) opera transitivamente sugli ideali primi nei quali p si fattorizza, sicché p risulta canonicamente associato a una classe di coniugio di sottogruppi di G(ϑ). Non soltanto questo risultato continua a sussistere per estensioni di Galois relative, ma inoltre si può dimostrare che il sottogruppo è ciclico con un generatore canonico. L'elemento del gruppo di Galois relativo così associato con ogni ideale primo nel corpo di base K che non è ramificato nell'estensione si chiama ‛automorfismo di Frobenius' ed è determinato a meno di un coniugio. Naturalmente, quando G(ϑ) è commutativo, ogni classe di coniugio contiene proprio un elemento, cosicché l'automorfismo di Frobenius è un elemento ben definito del gruppo di Galois. Gli elementi dei gruppi di classi di divisori di congruenze, nella loro definizione originale, sono classi di ideali e ciascun primo non ramificato appartiene a una di queste classi. Artin riuscì a dimostrare che, quando G(ϑ) è commutativo, l'automorfismo di Frobenius dipende soltanto dalla classe alla quale l'ideale primo appartiene e l'applicazione che risulta, dalle classi di ideali a G(ϑ), è l'isomorfismo cercato. Questo teorema, che viene oggi considerato il risultato centrale della teoria, è strettamente legato alla legge di reciprocità quadratica e alle sue generalizzazioni. In casi particolari esso può essere dedotto dalla corrispondente legge di reciprocità, ma Artin riuscì a dare una dimostrazione diretta e a provare che tutte le leggi di reciprocità fino ad allora note ne erano dei facili corollari. Questo teorema, che è oggi noto come legge di reciprocità di Artin, fu da questi scoperto nel corso di una ricerca che costituisce un primo importante passo avanti nel campo delle leggi di decomposizione in ideali primi e della reciprocità per estensioni di corpi con gruppi di Galois non commutativi. Sia K un corpo di numeri algebrici e sia ζK(ϑ) la funzione zeta di un corpo estensione di Galois K(ϑ), con gruppo di Galois (relativo) G(ϑ). Sia p un ideale primo di K. Quando G(ϑ) è commutativo e p non è ramificato, un ragionamento molto elementare permette di provare che è possibile fattorizzare il contributo di p a ζK(ϑ) come prodotto, esteso ai caratteri χ di G(ϑ), delle funzioni
ove αp è l'automorfismo di Frobenius corrispondente a p. Quindi, a eccezione dei contributi dei primi ramificati, la funzione zeta può essa stessa essere fattorizzata come prodotto sui caratteri χ di G(ϑ) delle serie di Dirichlet La(χ, s), ove
e il prodotto al secondo membro è esteso agli ideali primi non ramificati. Artin osservò che questa fattorizzazione può essere generalizzata al caso non commutativo. Per ogni rappresentazione di dimensione finita α ???14??? Vα di G(ϑ) si può definire una serie di Dirichlet
e osservare che la funzione risultante di s è indipendente dalla scelta di α nella sua classe di coniugio e dipende soltanto dalla classe di equivalenza di V. Questa serie di Dirichlet (moltiplicata per il prodotto esteso sui primi ramificati, che non ci dilungheremo qui a descrivere) è la funzione L di Artin, L(s, χ), associata al carattere χ della rappresentazione V. Poiché si dimostra che L(s, χ1 + χ2) = L(s, χ1)L(s, χ2) è sufficiente determinare L(s, χ) per i caratteri irriducibili e la funzione zeta del corpo non è che la funzione L di Artin per il carattere della rappresentazione regolare. Ne segue che la funzione zeta ammette la fattorizzazione
ove il prodotto è esteso a tutti i caratteri irriducibili e dχ = χ(e). Sfortunatamente, L(s, χ) può essere identificata con una L-funzione generalizzata di Dirichlet soltanto per quei χ per i quali χ(e) = 1; non si conosce nessuna generalizzazione di questo risultato. D'altra parte Artin ha dimostrato che, se χ è indotto da un carattere ψ di un sottogruppo H, L(s, χ) coincide con la L-funzione di Artin L(s, ψ) per il corpo K(ϑ) considerato come un'estensione del corpo fissato di H. In base a questo fatto e ad altri, ai quali abbiamo accennato dianzi, si vede facilmente che ogni L-funzione di Artin è il quoziente di due prodotti finiti di L-funzioni generalizzate di Dirichlet, purché ogni carattere irriducibile di G(ϑ) possa essere scritto nella forma n1χ1 + ... + njχj, ove gli nj sono interi e i χj sono indotti dai caratteri a una dimensione di sottogruppi. Artin congetturò che questo fatto avrebbe potuto continuare a sussistere per i caratteri irriducibili di un gruppo arbitrario finito. Come abbiamo ricordato nel cap. 7, la dimostrazione di questa congettura, data da R. Brauer nel 1947, ha avuto una considerevole importanza negli ulteriori sviluppi della teoria dei gruppi finiti. Insieme ai risultati già noti sulle L-funzioni di Dirichlet, essa implica che le L-funzioni di Artin sono meromorfe in tutto il piano complesso. Artin congetturò inoltre che le sue L-funzioni siano intere ogniqualvolta il carattere che le definisce è irriducibile e diverso dall'identità. Questa congettura ha molte conseguenze interessanti, ma è stata dimostrata soltanto in alcuni casi particolari.
La nozione di gruppi di classi di idèle introdotta da Chevalley dipende dalla nozione di ‛numero p-adico' introdotta da Hensel all'inizio di questo secolo. Dato un numero primo ordinario p, ogni intero positivo può essere scritto come una somma a0 + a1p +... + akpk, ove gli aj sono interi non negativi minori di p. Le regole per addizionare e moltiplicare due interi positivi possono essere formulate in termini di aj e hanno senso anche quando vengono applicate a somme formali infinite a0 + a1p + ... + akpk + ... In tal modo, l'insieme di tutte queste somme formali diventa un anello commutativo con elemento unità, in cui il sottoanello generato da 1 è isomorfo agli interi ordinari. Come nel caso degli interi ordinari, i quozienti formali a/b definiscono gli elementi di un corpo, che prende il nome di corpo dei ‛numeri p-adici'. Ogni numero p-adico, x, può essere scritto in uno e un sol modo nella forma pk(a0 + a1p + ...), ove a0 ≠ 0 e k è un intero ordinario che indicheremo con Vp(x). Ovviamente Vp(xy) = Vp(x) + Vp(y) e Vp(x + y) ≤ Max (Vp(x), Vp(y)). Indicando con ρ(x, y) e-Vp(x-y) si ottiene una funzione distanza, o una metrica, la quale trasforma il corpo Qp dei numeri p-adici in uno spazio topologico. Rispetto a questa topologia, Qp è un corpo topologico nel senso che le operazioni del corpo sono continue. Inoltre, come spazio topologico, esso è separabile, localmente compatto e totalmente sconnesso. I numeri p-adici per i quali Vp(x) ≥ 0 prendono il nome di interi p-adici. Essi formano un sottoanello compatto aperto che è la chiusura dell'immagine isomorfa dell'anello degli interi ordinari ottenuta considerando il sottoanello generato da 1. Il sottocorpo generato da 1 è isomorfo al corpo dei numeri razionali e ha, come chiusura, l'intero corpo Qp. Quindi Qp può essere considerato come il ‛completamento' di Q rispetto alla metrica x, y ???14??? e-Vp(x-y). Inversamente, sia α un isomorfismo arbitrario di Q su di un sottocorpo denso di un corpo topologico ℱ, localmente compatto non discreto totalmente sconnesso. Si può dimostrare che esiste uno e un solo numero primo p e un isomorfismo β di ℱ su Qp, tale che r ???14??? β(α(r)) sia l'isomorfismo, univocamente determinato, di Q sul sottocorpo di Qp generato da 1.
Più in generale, sia K = Q(ϑ) il corpo estensione finita di Q. Per ogni ideale primo p nell'anello degli interi Z(ϑ) si può introdurre una metrica in K e ottenere un ‛completamento' di K, rispetto a questa metrica, che è un corpo topologico K, localmente compatto, separabile e totalmente sconnesso. Esso prende il nome di corpo dei numeri p-adici. Se p è contenuto nella fattorizzazione dell'ideale principale generato dal numero primo ordinario p, la chiusura Ö di Q in Kp è isomorfa al corpo dei numeri p-adici e Kp è uno spazio vettoriale di dimensione finita su Q. Inversamente, se a è un isomorfismo arbitrario di K su un sottocorpo denso di un corpo localmente compatto e totalmente sconnesso ℱ, esiste uno e un solo ideale primo p e un isomorfismo β di ℱ su K, tale che x ???14??? β(α(x)) è l'immersione di K in Kp descritta dianzi.
Il gruppo idèle JK di K è il prodotto diretto di altri due gruppi chiamati rispettivamente componente archimedea e non archimedea di JK. La componente non archimedea JnK è un sottogruppo del prodotto diretto esteso agli ideali primi p di K dei gruppi moltiplicativi K*p degli elementi non nulli dei corpi di numeri p-adici Kp. Si dice che un elemento x di Kp è un'‛unità' se esso sta nella chiusura dell'anello degli interi di K ed è un'unità in questo anello. L'insieme di tutte le unità è un sottogruppo compatto aperto Up di K*p e il sottogruppo JnK di Π K*p è definito dalla condizione che la sua p componente xp deve appartenere a Up per tutti i p a eccezione di un numero finito. Per far diventare Πp Up ⊆ JnK un gruppo compatto, s'introduce in esso la topologia più debole per la quale le proiezioni sulle sue componenti siano continue; si attribuisce quindi a JnK la topologia ‛univocamente definita' per la quale Πp Up è un aperto e la cui restrizione a quest'ultimo è la topologia compatta appena descritta. Poiché ogni x nel gruppo moltiplicativo K* di K ha un'immagine canonica in ogni Kp, si ottiene un omomorfismo canonico hn di K* in JnK. Per definire la componente archimedea JaK di JK si osserva che, eliminando la restrizione che ℱ sia totalmente sconnesso, si possono trovare altre immersioni dense di K in corpi localmente compatti ℱ. Sia P un polinomio a coefficienti razionali di grado minimo tale che P(ϑ) = 0 e siano ϑ1, ..., ϑr i punti x del piano complesso tali che P(x) = 0 e che x abbia parte immaginaria non negativa. Sia ℱj il corpo dei numeri reali o dei numeri complessi secondo che ϑj sia reale oppure no. Esiste allora uno e un solo isomorfismo βj di K su di un sottocorpo denso di ℱj tale che βj(ϑ) = ϑj e, a meno di un'ovvia equivalenza, non ne esistono altri in cui ℱ sia localmente compatto ma non totalmente sconnesso. Si definisce allora JaK come
ove ℱ*j è il gruppo moltiplicativo di ℱj. Il gruppo idèle JK è allora JnK × JaK. L'isomorfismo x ???14??? hn(x), γ1(x), ..., γr(x), di K* in JK permette di identificare K* con un sottogruppo di JK e si può dimostrare che questo sottogruppo è chiuso. I suoi elementi si chiamano ‛idèle principali' e il ‛gruppo di classi di idèle' CK è, per definizione, il gruppo quoziente JK/K*. Si può dimostrare che esso è compatto.
Il gruppo Πp Up × JaK è un sottogruppo aperto UK di JK. La sua immagine in CK è un sottogruppo aperto il cui gruppo quoziente (necessariamente finito) è isomorfo al gruppo delle classi di ideali di K.
Avendo definito il gruppo delle classi di idèle CK come il gruppo quoziente di un sottogruppo di un gruppo prodotto infinito, il problema di trovare i gruppi quozienti di indice finito di CK, e quindi le possibili estensioni abeliane di Galois di K, si riduce in parte a trovare i gruppi quozienti di ordine finito dei gruppi componenti K*p e ℱ*j. Difatti si può dimostrare che esiste una versione ‛locale' della teoria che collega le estensioni di Galois commutative di ogni corpo localmente compatto non discreto separabile ai gruppi quozienti di indice finito del suo gruppo moltiplicativo. Si dimostra anche che la ‛versione globale' si può considerare come un ‛composto' della versione locale e del teorema secondo il quale una famiglia di gruppi quozienti locali ne definisce una globale se, e soltanto se, il nucleo del gruppo quoziente corrispondente di JK contiene K*. La parte ‛solo se' del teorema è essenzialmente la legge di reciprocità.
Strettamente connesso al gruppo idèle di K è un altro gruppo localmente compatto e sconnesso AK che si chiama gruppo adèle. Esso è definito come il gruppo idèle, eccetto che i gruppi additivi dei corpi Kp e ℱj sostituiscono quelli moltiplicativi e il gruppo additivo della chiusura dell'anello degli interi in Kp sostituisce il gruppo delle unità. Si ha un'immersione canonica del gruppo additivo di K in AK come sottogruppo chiuso con quoziente compatto.
Il gruppo AK, come gruppo commutativo localmente compatto, è isomorfo al suo duale ÂK, in modo tale che l'immagine di K è l'annullatore K⊥ in AK. In base a questo fatto e alla formula sommatoria di Poisson applicata a K e ad AK, J. Tate e, indipendentemente, K. Iwasawa trovarono una dimostrazione unificata delle equazioni funzionali per le L-funzioni associate ai caratteri generalizzati di Dirichlet per un corpo di numeri algebrici. Di fatto la dimostrazione vale per le L-funzioni associate ai caratteri arbitrari a una dimensione del gruppo delle classi di idèle, siano essi oppure no di ordine finito. Questi caratteri più generali, e le corrispondenti L-funzioni, vennero introdotti da E. Hecke mediante gruppi di classi di divisori di congruenze. Essi sono noti come Grössencharactere; Hecke d'altra parte aveva dimostrato le equazioni funzionali in modo assai più complicato.
Sia K = Q(ϑ) un corpo di numeri algebrici e sia G un gruppo di automorfismi di K. G opera in modo naturale come gruppo di automorfismi del gruppo delle classi di idèle CK di K. Analogamente, se G è un gruppo di automorfismi di un completamento p-adico Kp di K, esso agisce come un gruppo di automorfismi del gruppo moltiplicativo K*p di Kp. Considerando CKe K*p come G-moduli per varie scelte di G, si possono ricercare i corrispondenti gruppi di coomologia come sono stati definiti e discussi nel cap. 10. Una serie di ricerche iniziate intorno al 1950 a opera di Hochschild e continuate dallo stesso Hochschild, Nakayama, Tate e Artin portarono alla conclusione che questi gruppi di coomologia erano strettamente collegati alla teoria delle estensioni abeliane di Galois di corpi di numeri algebrici (teoria dei corpi di classi) che abbiamo precedentemente descritta. In ambedue i casi si può dimostrare che il gruppo di coomologia di dimensione uno è banale e quello di dimensione due è ciclico con ordine uguale a quello di G. Inoltre, questo gruppo ciclico ha un generatore canonico. D'altra parte questi fatti, tenuto conto delle ovvie relazioni fra i moduli associati a corpi e sottocorpi, implicano tutti i risultati globali e locali della teoria dei corpi di classi, a eccezione di quelli che affermano l'esistenza di un corpo estensione per ogni gruppo a quoziente finito. Tate riuscì inoltre a determinare tutti gli altri gruppi di coomologia collegandoli al primo e al secondo in un modo valido per ogni G-modulo avente certe proprietà di CK e K*p. Come abbiamo accennato nel cap. 10, questi risultati ebbero profonda influenza per i successivi sviluppi della coomologia dei gruppi.
Come abbiamo già detto, i risultati più interessanti nella teoria delle forme quadratiche binarie possono essere compresi senza difficoltà quando li si considerino come teoremi sulla fattorizzazione di ideali in corpi quadratici. In quest'ottica essi possono essere generalizzati a corpi numerici più generali. Questi risultati più comprensivi ne implicano altri su forme binarie di grado più elevato e sulla soluzione di equazioni diofantee del tipo A0xn + A1xn-1y + ... + Anyn = m. Tuttavia, invece di aumentare il grado e mantenere il numero delle variabili a due, si può mantenere il grado uguale a due e considerare forme quadratiche in n variabili (forme quadratiche n-arie).
Il caso n = 3 fu esaminato per la prima volta nel 1798 da Legendre nel suo libro e ampiamente sviluppato da Gauss nelle sue Disquisitiones. Nel 1828, inoltre, C. G. J. Jacobi ottenne una formula per il numero delle soluzioni intere dell'equazione χ²1 + χ²2 + χ²3 + χ²4 = m come conseguenza accidentale delle sue ricerche sulla teoria delle funzioni ellittiche. Questo ‛fortunato accidente' non fu pienamente compreso che nel XX secolo quando ci si accorse che esso è una conseguenza di una teoria generale molto profonda che collega le forme quadratiche con la teoria delle funzioni automorfe. Formule simili per somme di due, sei e otto quadrati seguono anch'esse dal lavoro di Jacobi. Poco meno di vent'anni più tardi F. G. Eisenstein trovò, nell'ambito della pura teoria dei numeri, una dimostrazione di tali formule nel caso di sei e otto quadrati e poco più tardi riuscì a trattare il caso delle somme di cinque e sette quadrati. Uno studio sistematico del caso n-ario fu iniziato da Ch. Hermite nel 1851 e proseguito da H. J. Smith, H. Minkowski e J. H. Poincaré. Un resoconto comprensivo dei loro risultati si trova nel trattato di Bachman del 1898.
Sia
una forma quadratica con aij = aji e aij interi.
Due forme siffatte si dicono equivalenti se esiste una matrice ∥ bij ∥ a elementi interi e determinante ± 1 tale che la sostituzione xj ???14??? Σbjkxk trasformi una delle due forme quadratiche nell'altra. Nell'ambito della teoria dei numeri non è necessario distinguere tra forme equivalenti. Uno dei maggiori problemi consiste nel determinare quando due forme sono equivalenti e quanto sia possibile semplificarle o ‛ridurle' senza alterare la loro classe di equivalenza. Il determinante della matrice ∥ aij ∥ si chiama ‛determinante' della forma ed è ‛invariante', nel senso che forme equivalenti hanno sempre lo stesso determinante. Un risultato rilevante, stabilito mediante la teoria della riduzione, è che esiste soltanto un numero finito di classi di equivalenza corrispondenti a un dato valore non nullo del determinante. Le forme quadratiche vengono ‛classificate' trovando altri invarianti in numero sufficiente affinché due forme aventi gli stessi invarianti stiano necessariamente nella stessa classe e determinando criteri per decidere quali valori di tali invarianti si presentino effettivamente per forme quadratiche. Per ogni data classe di forme quadratiche, il problema fondamentale è naturalmente quello della rappresentazione: per quali interi n l'equazione diofantea Σ aijxixj = n ha soluzioni e quante sono queste soluzioni? In molti casi il numero delle soluzioni risulta infinito non appena esso è diverso da zero e il problema della rappresentazione può allora essere precisato chiedendo il numero delle ‛classi di soluzioni'. Due soluzioni vengono poste nella stessa classe quando vi sia una matrice che stabilisca un'equivalenza di Σ aijxixj con se stessa e che porti una soluzione nell'altra. (Tale trasformazione viene chiamata, nella letteratura classica, automorfia). Si può dimostrare che il numero delle classi di soluzioni è sempre finito. Più in generale, date due forme quadratiche Σ aijxixj e Σ bijyiyj, rispettivamente in n e m variabili, una rappresentazione dell'una mediante l'altra è per definizione una matrice n × m a elementi interi wij tale che, posto yj = Σ wjlxl, si passa dall'una all'altra. Determinare tutte le rappresentazioni equivale a risolvere un sistema di m(m − 1)/2 equazioni quadratiche diofantee in nm variabili. A questo punto si distribuiscono le soluzioni in classi mediante automorfie; si dimostra che il numero delle classi delle soluzioni è finito; si cercano dei metodi per calcolare questo numero o, più precisamente, il numero delle classi di soluzioni ‛primitive'.
Si dice che due forme quadratiche stanno nello stesso se, per ogni intero positivo q, ciascuna di esse può essere rappresentata dall'altra, nel senso citato dianzi, mediante matrici non singolari i cui elementi sono numeri razionali aventi denominatori primi con q. Forme quadratiche nello stesso genere hanno necessariamente lo stesso determinante, così che ogni genere contiene soltanto un numero finito di classi. I risultati precisi che valgono per i numeri delle classi di soluzioni primitive delle equazioni diofantee descritte dianzi si riferiscono al caso particolare in cui il genere della forma rappresentativa contiene soltanto una classe. Più in generale, si hanno formule soltanto per la somma estesa a tutte le classi nel genere. Le forme quadratiche x²1 + x²2 + ... + x²t, per t ≤ 8, sono tali che ciascuna di esse ha soltanto una classe nel suo genere e i risultati di Eisenstein relativi a somme di cinque, sei, otto quadrati sono corollari della teoria generale sviluppata da Smith, Minkowski e Poincaré.
Sia n ???14??? ϕ(n) una funzione definita nell'ambito della teoria dei numeri a partire da interi non negativi e a valori interi non negativi, quale il numero delle classi di rappresentazioni di n mediante una forma quadratica. Sia
la cosiddetta ‛funzione generatrice'. In molti casi questa serie converge nel cerchio unità. Uno studio dettagliato di φ̃ vicino alla frontiera si può sviluppare direttamente a partire dalla definizione di ϕ. Applicando la formula di Cauchy per riottenere ϕ a partire da φ̃, mediante delle valutazioni delicate si ottengono delle funzioni di n calcolabili esplicitamente che sono asintotiche a ϕ per n sufficientemente grande. Questa tecnica (nota come metodo del cerchio) fu introdotta nel 1917 da Hardy e Ramanujan, i quali se ne servirono per ottenere una formula asintotica per il numero P(n) dei modi di scrivere n come somma di interi positivi più piccoli. Poco più tardi Hardy e J. E. Littlewood usarono questa tecnica per ottenere espressioni asintotiche per il numero Srk(n) dei modi di scrivere n come somma di r potenze k-esime. Nel caso particolare delle somme dei quadrati, Hardy dimostrò che i risultati asintotici erano di fatto esatti per 5 ≤ r ≤ 8, utilizzando certi aspetti della teoria delle funzioni automorfe. Qualche tempo dopo, nel 1927, Hecke provò che era possibile estendere in una certa misura quest'ultima teoria e applicarla per ottenere i risultati di Hardy e Littlewood sulle somme di quadrati, in un modo molto più semplice ed elegante. Il punto di partenza sta nel fatto che, per ϕ(n) = Sr2(n), una ben nota argomentazione che si basa sulla formula sommatoria di Poisson (e strettamente connessa al ragionamento usato per stabilire le equazioni funzionali per le funzioni zeta e le L-funzioni) permette di dimostrare che la funzione
z ???14??? φ̃(e2πmz) = f(z)
soddisfa l'equazione funzionale
che definisce una ‛forma automorfa di peso r/4', per ogni zeta appartenente al semipiano superiore e per tutte le
in un certo sottogruppo discreto del gruppo SL(2, R). D'altra parte, Hecke riuscì a provare che f ha certe proprietà di regolarità quando z si avvicina all'asse reale e riuscì a dare una costruzione diretta della soluzione più generale dell'equazione funzionale, soddisfacente queste condizioni di regolarità. La costruzione diretta è tale che si possono ‛leggere' direttamente le espressioni richieste per ϕ(n). Daremo ulteriori dettagli nel cap. 15. Inoltre, lo stesso tipo di ragionamento può essere applicato quando x²1 + ... + x²n è sostituita da un'arbitraria forma quadratica definita positiva a coefficienti interi.
Otto anni più tardi, nel 1935, Hecke fece una profonda osservazione che collegava l'uso delle forme automorfe, descritte dianzi, alle serie di Dirichlet e alle L-funzioni che si presentavano nella teoria dei corpi di numeri algebrici.
Supponiamo che
sia definita per z nel semipiano superiore e consideriamo la funzione y ???14??? f(iy) sull'asse reale positivo. Il carattere più generale del gruppo moltiplicativo dei numeri reali positivi è y ???14??? ys ove s è un numero complesso. Corrispondentemente la ‛trasformata di Fourier' di y ???14??? f(iy) è
nota di solito sotto il nome di trasformata di Mellin. Una analisi elementare mostra che la trasformata di Mellin di y ???14??? e2πiniy = e-2πny è
cosicché, quando sia possibile integrare termine a termine, la trasformata di Mellin di y ???14??? f(iy) è
In altre parole, la trasformata di Mellin di
è
volte la serie di Dirichlet
Inoltre, semplici considerazioni mostrano che
vale per tutti gli
in SL(2, R), con a, b, c, d interi, se, e soltanto se, le serie di Dirichlet possono essere prolungate analiticamente in una funzione D(s) soddisfacente l'equazione funzionale
Sulla base di questo risultato e di certe sue estensioni e miglioramenti, Hecke riuscì a dimostrare che l'equazione funzionale per certe funzioni zeta e L-funzioni ha soltanto una varietà lineare di dimensione finita di soluzioni (fra le funzioni soddisfacenti opportune condizioni di limitatezza) e che queste funzioni possono essere espresse esplicitamente mediante la teoria delle corrispondenti forme automorfe. D'altra parte, egli riuscì a dimostrare che la varietà lineare di tutte le forme automorfe di un certo peso ha una base di forme le cui serie di Dirichlet corrispondenti ammettono fattorizzazioni in prodotti di Eulero. Applicando questo risultato alle forme automorfe associate alle forme quadratiche, ottenne risultati del tipo
ove c è una costante nota, ζ(s) = Σ 1/ns e ζ(s)L(s) è la funzione zeta di Q(√-−-1). Utilizzando i prodotti di Eulero per ζ e L, si può naturalmente calcolare S26(n) per questa formula per ogni n, fattorizzando n. Mediante questo legame tra teoria dei gruppi e teoria delle forme automorfe, queste ricerche di Hencke collegarono la teoria dei gruppi alla teoria delle forme quadratiche nonché, in modo del tutto originale, alla teoria dei corpi di numeri algebrici.
Una forma quadratica a coefficienti interi può anche essere considerata come una forma quadratica a coefficienti razionali. Per forme quadratiche a coefficienti in un corpo ℱ è naturale definire due forme come equivalenti quando esiste una matrice non singolare ∥ aij ∥, ad elementi in ℱ, tale che la sostituzione xj ???14??? Σ ajkxk porti una nell'altra. Forme equivalenti sono naturalmente equivalenti sui razionali, ma non viceversa. Si può pertanto dividere il problema della classificazione in due parti: prima classificare le forme sui razionali e quindi trovare le classi intere in ciascuna classe razionale. Nessuno dei due problemi è banale e la divisione si rivelò vantaggiosa anche se dovette passare un po' di tempo prima che ci se ne accorgesse. In particolare il problema razionale può essere risolto con un metodo particolarmente elegante, scoperto da Minkowski.
All'inizio del 1920 H. Hasse mostrò che molti aspetti della teoria delle forme quadratiche divengono più semplici quando s'introducono i numeri p-adici. Egli formulò elegantemente il risultato di Minkowski citato dianzi nel modo seguente: due forme quadratiche a coefficienti razionali sono equivalenti sui razionali se, e soltanto se, sono equivalenti sul corpo dei numeri reali e anche sul corpo dei numeri padici per ogni numero primo p. Poiché la classificazione sui numeri reali è ben nota ed elementare e la classificazione sui numeri p-adici è anch'essa relativamente semplice, si ottiene la classificazione più complicata delle forme quadratiche sui razionali specificando quali sistemi di invarianti reali e p-adici intervengono di fatto. È naturale cercare di trovare lo stesso tipo di soluzione per la classificazione delle forme quadratiche sugli interi. Purtroppo, però, il ‛principio di Hasse' non vale in questo caso. Si trova invece che condizione necessaria e sufficiente perché due forme siano equivalenti sugli ‛interi' p-adici per tutti i p e sui numeri reali è che esse stiano nello stesso genere. Hasse considerò inoltre forme quadratiche su corpi di numeri algebrici e sopra gli anelli di interi in corpi di numeri algebrici e trovò risultati simili nei quali compaiono numeri p-adici, ove p varia tra gli ideali primi dell'appropriato anello di interi. Infine Hasse considerò il problema di rappresentare una forma quadratica mediante un'altra e scoprì che il ‛principio di Hasse' vale per le rappresentazioni razionali: una rappresentazione di una forma per un'altra sui razionali esiste se, e soltanto se, una rappresentazione esiste sui numeri reali e sui p-adici per tutti i primi p. Per rappresentazioni di una forma mediante un'altra sugli interi, il principio di Hasse vale se, e soltanto se, si considerano simultaneamente tutte le forme in un dato genere e si cerca una rappresentazione per almeno una forma nel genere.
I risultati di Hecke e di Hasse vennero unificati ed estesi in modo considerevole in una serie importante di lavori di C. L. Siegel pubblicati negli anni 1935, 1936 e 1937. Lo scopo di Siegel era quello di raffinare il principio di Hasse in modo da ottenere una formula che esprimesse il numero delle rappresentazioni di una forma mediante un'altra in funzione delle ‛densità di soluzioni' nel corpo reale e nel corpo dei numeri p-adici. Contando, come abbiamo spiegato dianzi, classi di soluzioni invece di soluzioni, Siegel riuscì a mostrare che la somma dei numeri di soluzioni sopra tutte le classi di forme in un dato genere è una certa costante moltiplicata per un prodotto infinito i cui fattori possono interpretarsi come ‛densità di soluzioni' sui numeri reali e sui numeri p-adici. Inoltre Siegel si collegò a metodi analitici mostrando che i suoi risultati erano del tutto equivalenti a un'identità relativa a due forme automorfe in più variabili complesse. Nel caso particolare in cui si rappresenta un numero mediante una forma, si ha a che fare soltanto con una variabile complessa e una delle due forme automorfe è la ‛serie theta'
ove ϕ(n) è la somma estesa a un genere dei numeri di soluzioni normalizzate. L'altra forma automorfa è la cosiddetta ‛serie di Eisenstein', una serie la cui somma (a differenza della serie theta) è evidentemente una forma automorfa che può essere scritta esplicitamente quando siano noti i coefficienti della forma quadratica. L'opera di Hecke aveva implicato la dimostrazione del fatto che la serie theta per una singola forma quadratica è la somma di una ‛forma cuspidale' e di una serie di Eisenstein. Pertanto le forme cuspidali si elidono quando si sommano tutte le classi in un dato genere. Siegel dovette sviluppare le opportune generalizzazioni della teoria delle forme automorfe da una a più variabili complesse. Egli ritornò più volte su queste generalizzazioni negli anni successivi e diede il via a una teoria che è ancora in fase di sviluppo.
Sia ℱ un corpo di caratteristica ≠ 2 e sia
una forma quadratica a coefficienti in ℱ. La Σ aijxixj definisce un funzionàle simmetrico bilineare sullo spazio vettoriale di tutte le n-uple di elementi di ℱ. Per questa ragione esso viene talora chiamato uno ‛spazio quadratico' su ℱ. Ciò significa uno spazio vettoriale su ℱ insieme con una particolare forma simmetrica bilineare v1, v2 ???14??? (v1•v2). Definendo in modo ovvio l'isomorfismo di spazi quadratici, si vede immediatamente che due forme quadratiche su ℱ sono equivalenti su ℱ se, e soltanto se, gli spazi quadratici corrispondenti sono isomorfi. Lo studio delle forme quadratiche, basato sugli spazi quadratici da esse definiti, conduce a un punto di vista interessante che fu per la prima volta messo in evidenza da E. Witt in un importante lavoro pubblicato nel 1937. Esso venne ripreso in dettaglio da M. Eichler, che riscrisse una larga parte della teoria in termini di spazi quadratici in un libro, Quadratische Formen und orthogonale Gruppen, che apparve nel 1952. Fra l'altro, il punto di vista degli spazi quadratici pone in evidenza delle strette relazioni con la teoria dei gruppi che erano rimaste fino ad allora nell'ombra. Si dice che uno spazio quadratico V, (•) è semisemplice se (v•w) = o per tutti i w implica che v = 0. Non si perde niente di essenziale in generalità se si limita l'attenzione al caso semisemplice. Il gruppo degli automorfismi di uno spazio quadratico semisemplice è naturalmente uno dei gruppi ortogonali citati nel cap. 3; questo gruppo non soltanto è determinato a meno di un isomorfismo dallo spazio, ma in larga misura determina lo spazio stesso. Se due gruppi ortogonali sono isomorfi come gruppi astratti, i corpi su cui sono definiti sono isomorfi. Quando essi sono opportunamente identificati, si può far diventare uno dei due spazi quadratici un'immagine isomorfa dell'altro moltiplicando semplicemente la sua forma bilineare per una costante. Pertanto classificare le forme quadratiche rispetto all'equivalenza sopra un corpo è in larga misura lo stesso che classificare certi gruppi semplici classici. Sia O il gruppo degli automorfismi (gruppo ortogonale) dello spazio quadratico V, (•) sopra il corpo Q dei numeri razionali. Sia ϕ1, ϕ2, ..., ϕr una base di V su Q tale che (ϕi•ϕj) sia un intero per tutti gli i e j. Lo spazio quadratico V, (•)è determinato da una forma quadratica a coefficienti interi e ogni forma a essa equivalente su Q può essere ottenuta da V, (•) scegliendo opportunamente una base ψ1, ψ2, ..., ψn. Siano L1 e L2 i sottogruppi del gruppo additivo di V generati rispettivamente da ϕ1, ..., ϕn e ψ1, ..., yn. Si vede facilmente che le forme quadratiche Σ xixj(ϕi•ϕj) e Σ xixj(ψi•ψj) sono equivalenti ‛sugli interi' se, e soltanto se, esiste un elemento di O che trasforma L1 in L2; cioè se, e soltanto se, L1 e L2 sono sottogruppi coniugati del prodotto semidiretto naturale di O e del gruppo additivo di V. Ne segue che la classificazione delle classi intere in una data classe razionale di forme quadratiche è completamente equivalente al problema di pura teoria dei gruppi consistente nel decomporre certi sottogruppi commutativi di V ???30??? O in classi coniugate. Come fu osservato da Eichler, si può pensare a V ???30??? O come a un analogo del gruppo dei movimenti rigidi dello spazio e alla determinazione delle classi intere delle forme quadratiche come all'analogo del problema della classificazione dei reticoli cristallini. Eichler osservò inoltre che esiste un certo parallelismo tra la teoria dei corpi di numeri algebrici e la teoria delle forme quadratiche in cui i ruoli del gruppo additivo e del gruppo moltiplicativo del corpo numerico sono sostenuti da V e da O rispettivamente.
Quest'osservazione di Eichler suggerisce che si potrebbe ottenere una certa unificazione tra la teoria dei numeri algebrici e quella delle forme quadratiche, considerando i sistemi V, L e G costituiti da uno spazio vettoriale di dimensione finita V sui razionali, un sottogruppo L del gruppo additivo di V generato da una base di V e un sottogruppo G del gruppo di tutte le trasformazioni lineari non singolari di V in se stesso. In un lavoro pubblicato nel 1957, T. Ono fece un importante passo avanti nella realizzazione di questo programma generalizzando la nozione di gruppo idèle in modo da poterla applicare a qualsiasi sistema V, L, G in cui G sia algebrico sui razionali (si confronti in proposito il cap. 9). Egli trovò un enunciato relativo a questi gruppi idèle generalizzati, che contiene come casi particolari il teorema sulla finitezza del gruppo delle classi di ideali e quello sulla finitezza del numero delle classi di forme quadratiche in un genere. Per ogni numero primo p si ha un immersione naturale densa di V in uno spazio vettoriale di dimensione finita Vp sui numeri p-adici e le espressioni polinomie che definiscono il gruppo algebrico G definiscono un sottogruppo algebrico Gp del gruppo delle trasformazioni lineari non singolari di Vp in se stesso. La chiusura in Vp di L è un sottogruppo compatto aperto di Vp e il sottogruppo di Gp che trasforma questo sottogruppo su se stesso è un sottogruppo compatto aperto Gop del gruppo totalmente sconnesso Gp. In modo analogo si definisce G∞ mediante l'immersione naturale di V in uno spazio vettoriale di dimensione finita sui numeri reali. Il gruppo di Ono delle ‛G-idèle' (chiamato ora il gruppo adèle) è il sottogruppo J del prodotto diretto
costituito da tutti gli elementi le cui p-componenti stanno in Gop a eccezione di un numero finito di valori di p. Il sottogruppo J∞ di tutti gli elementi le cui p-componenti stanno in Gop per tutti i numeri primi p è il prodotto diretto
e, come prodotto diretto di G∞ e di un gruppo compatto, ha una topologia compatta naturale. Si topologizza J in modo che J∞ sia aperto e abbia la topologia testè definita. Poiché G ha un immersione naturale in G∞ e in ogni Gp, esso ha un'immersione naturale in J. Si dimostra che l'immagine in J è chiusa e la s'identifica con G. Nel caso particolare in cui V e G sono i gruppi additivo e moltiplicativo in un corpo di numeri algebrici k e L è il gruppo additivo degli interi in k, il gruppo adèle J coincide con il gruppo idèle che abbiamo definito precedentemente. Le classi laterali doppie J∞: G corrispondono in modo biunivoco agli elementi del gruppo quoziente di J/G per l'immagine di J∞ in J/G e quindi agli elementi del gruppo della classe di ideali di k. D'altra parte, quando V, L, G provengono da una forma quadratica, queste classi laterali doppie corrispondono alle diverse classi di forme nel genere della forma data. Pertanto, un opportuno teorema generale sulla finitezza dell'insieme delle classi laterali doppie J∞: G in J per ogni sistema V, L, G conterrebbe, come casi particolari, il teorema sulla finitezza del gruppo delle classi di ideali e del numero delle classi in un genere di forme quadratiche. Un tale teorema fu dimostrato da Borel in un lavoro pubblicato nel 1963, sulla base di teoremi dovuti a Borel stesso e ad Harish-Chandra, che generalizzavano teoremi classici sulla teoria della riduzione delle forme quadratiche. I risultati di Siegel sulle forme quadratiche, dei quali abbiamo parlato dianzi, vennero inseriti nell'ambito del gruppo adèle da ricerche indipendenti di Tamagawa e M. Kneser. Utilizzando la struttura speciale di un gruppo adèle, si dimostra che in molti casi la costante arbitraria nella misura di Haar può essere scelta canonicamente, così che si può parlare senza ambiguità della misura di J/G. Questo numero prende il nome di ‛numero di Tamagawa' del gruppo algebrico in questione e il fatto che esso sia 2 per il gruppo ortogonale appropùato risulta essere sostanzialmente equivalente al teorema di Siegel. Ricerche successive di Weil e altri hanno determinato il numero di Tamagawa per svariati altri gruppi algebrici. Questi risultati inducono ad ampliare il programma di Eichler di unificare la teoria dei numeri algebrici e la teoria delle forme quadratiche in un programma più ambizioso volto a ottenere questi risultati come corollari di teoremi generali sui gruppi algebrici e i loro gruppi adèle. Progressi notevoli in questa direzione si sono ottenuti negli ultimi quindici anni. Un aspetto importante è stato lo sviluppo della teoria degli ‛spazi omogenei principali' per i gruppi algebrici. Sia A un gruppo algebrico definito su di un corpo k e sia Ω la chiusura algebrica di k (chiusura separabile se k non è perfetto). Sia G il gruppo degli automorfismi di Ω che lasciano invariati gli elementi di k. Ciascun elemento di G definisce un automorfismo di A e il sottogruppo A di quegli elementi a di A lasciati invariati dagli elementi di G è proprio il gruppo dei punti k razionali di A. Indichiamo con AG il prodotto semidiretto di A e Gefinito dalla azione assegnata di G su A. Un ‛A-spazio principale omogeneo' definito su k è un AG-spazio V dotato delle seguenti due proprietà: 1) l'azione di A è libera e transitiva; 2) per ogni v in V il sottogruppo di G che lascia v invariato è aperto in G. I punti ‛k-razionali' di V sono i punti di V invarianti per l'azione di G. Se l'insieme dei punti k-razionali non è vuoto, V è equivalente, come AG-spazio, ad A stesso, ove l'azione sia la traslazione destra. Possono tuttavia esistere A-spazi omogenei principali i quali non hanno punti k-razionali; la teoria riguarda allora la loro classificazione come AG-spazi. Molti importanti problemi della teoria dei numeri, come della teoria dei gruppi algebrici, si riducono alla classificazione degli spazi omogenei principali. D'altra parte, il problema della classificazione è esso stesso equivalente a un problema nella teoria coomologica dei gruppi. Per definizione, un ‛uno cociclo' è una funzione A da G a A tale che A(xy) = A(x) x[A(y)] per tutti gli x, y in G. Per definizione i cocicli A1 e A2 sono coomologhi se esiste un elemento a di A tale che A2(x) = a-1A1(x) x[a]. Si vede facilmente che le classi di coomologia degli uno cocicli corrispondono biunivocamente alle classi di equivalenza degli AG-spazi che soddisfano la condizione 1) dianzi menzionata. Inoltre, quelli che soddisfano anche la 2) corrispondono agli uno cocicli che sono costanti sulle classi laterali di un sottogruppo G di indice finito. Si osservi che il gruppo A non deve necessariamente essere commutativo, ma, quando lo è, le classi di coomologia formano un gruppo isomorfo a quello considerato nel cap. 10. Più in generale, si parla di un ‛insieme di coomologia'. In applicazioni alla teoria dei numeri ha particolare interesse il caso speciale in cui il corpo k è un corpo di numeri algebrici o il completamento di esso rispetto a un ideale primo p. Se kp è un tale completamento di k e Ap è il gruppo algebrico definito su kp corrispondente a A, esiste un'applicazione naturale dell'insieme di coomologia H′(A, k) per A e k in quello per Ap e kp e quindi nel prodotto degli H′(Ap, kp) esteso a tutti i p. Uno degli obiettivi principali è quello di cercare condizioni su A, le quali assicurino che questa applicazione è iniettiva ‛rincipio di Hasse) o, per lo meno, che l'immagine inversa di ogni punto è finita. In tutta generalità, Borel e Serre hanno dimostrato che H′(Ap, kp) è finito.
L'unificazione della teoria dei numeri algebrici e della teoria delle forme quadratiche attraverso una teoria di gruppi adèle di gruppi algebrici non commutativi rese imperativo ottenere una migliore conoscenza della struttura degli analoghi p-adici e p-adici dei gruppi di Lie semisemplici. In parte, risultati di questo tipo potrebbero essere ottenuti dallà teoria generale dei gruppi algebrici, ma i numeri p-adici e le loro estensioni algebriche finite sono corpi separabili localmente compatti che sotto molti aspetti sono vicini, nelle loro proprietà, al corpo dei numeri reali e a quello dei numeri complessi. Ci si aspetta che i gruppi algebrici semisemplici definiti su essi abbiano in comune delle proprietà con i gruppi di Lie semisemplici che non appartengono ai più generali gruppi di Lie semisemplici algebrici. In particolare, si vorrebbe un analogo del teorema di decomposizione di Iwasawa e del teorema secondo cui sottogruppi compatti massimali sono mutuamente coniugati. Furono Bruhat e Tits che scoprirono questi fatti piuttosto complicati e li annunciarono in una serie di note pubblicate nel 1966. Un ruolo chiave è sostenuto dalla nozione di coppia B-N introdotta nel 1965 da Iwasawa e Matsumoto. Un resoconto sommario potrà trovarsi nella conferenza di Bruhat al congresso di Nizza del 1970.
L'opera di Hecke che collegò le forme automorfe alle serie di Dirichlet condusse a un altro sviluppo molto importante, che sarà più opportuno descrivere nel cap. 15. In breve, un lavoro di H. Maass pubblicato nel 1949 introdusse ‛forme automorfe non analitiche' come mezzo per portare le funzioni zeta di forme quadratiche indefinite nell'ambito di una teoria del tipo di quella di Hecke. Nel 1956, Selberg, in un lavoro molto importante per gli sviluppi successivi, mostrò che le idee di Maass potevano essere generalizzate e meglio comprese considerando le forme automorfe da un punto di vista che le collegava strettamente alla teoria delle rappresentazioni unitarie di un gruppo. In questa visione rientravano vari aspetti della teoria dei numeri, della teoria delle forme automorfe e delle rappresentazioni unitarie dei gruppi, nelle quali la nozione di gruppo adèle sosteneva un ruolo importante. Molti matematici si dedicarono a queste ricerche e fra di essi in modo particolare Gelfand, Harish-Chandra, Weil, Langlands e Jacquet. Ulteriori dettagli verranno dati nel cap. 15.
14. Teoria dei gruppi e analisi armonica.
L'analisi armonica, nella sua forma classica, si occupa della teoria e delle applicazioni del fatto che ogni funzione a valori reali f di una variabile reale, periodica con periodo 2π/t e non ‛troppo irregolare', è la somma di una serie in- finita della forma
ove
e
Il termine ‛analisi armonica' deriva naturalmente dall'osservazione che la possibilità di uno sviluppo di questo tipo è l'equivalente matematico del fatto intuitivo secondo cui ogni nota musicale risulta da una sovrapposizione di una nota ‛fondamentale' e delle sue ‛armoniche superiori'. Per quanto queste estensioni appaiano già in scritti anteriori, Fourier sembra essere stato il primo, nel 1807, a rendersi conto dell'esistenza di un teorema generale e a stabilire le formule precedenti relative ai coefficienti aj e bj. È in suo onore che si parla di ‛serie di Fourier' e si usa il termine ‛analisi di Fourier' come sinonimo di analisi armonica. Fourier fu soprattutto un matematico applicato e si servì del suo ‛teorema' come di uno strumento nella discussione della teoria della trasmissione del calore. Egli non riuscì a dimostrarlo, neanche per quelli che erano i livelli di rigore dell'epoca, e si accese di fatto una polemica sostanziale relativa alla sua validità, che condusse alla moderna nozione di funzione, distinta da quella di formula e, successivamente, allo sviluppo della teoria delle funzioni di una variabile reale. Tenendo conto dei legami di Lagrange con le origini della teoria dei gruppi e con la teoria delle forme quadratiche binarie, è interessante osservare che nel 1759 egli si servì delle serie di Fourier in un importante articolo sulla teoria delle corde vibranti e pare che non si sia accorto del teorema di Fourier e delle sue formule per i coefficienti soltanto per la sua grande attenzione al rigore logico. Ricorrendo alle funzioni complesse e all'identità eix = cos x + i sen x, il teorema dello sviluppo di Fourier prende la forma
ove
e in questa forma è evidente il suo significato nell'ambito della teoria dei gruppi. Una funzione con periodo 2π/t può essere considerata come una funzione sul gruppo quoziente R/Zt, ove R è il gruppo additivo dei numeri reali e Zt è il sottogruppo chiuso di tutti i multipli interi di 2π/t. Inoltre, le funzioni x ???14??? eintx, per n = 0, ± 1, ± 2, ..., non sono altro che i caratteri a una dimensione di R/Zt. Pertanto essi determinano sottospazi di dimensione 1, invarianti per traslazione, degli spazi di Hilbert ℒ2(R/Zt, dx) e si può considerare il teorema di Fourier applicato alle funzioni di quadrato sommabile come l'enunciato che descrive la decomposizione in componenti irriducibili della rappresentazione regolare del gruppo compatto R/Zt. Quest'osservazione, insieme al vasto campo di applicazioni dell'analisi di Fourier classica, suggerisce che, ogniqualvolta si incontrino funzioni a quadrato sommabile definite su un gruppo, sia vantaggioso considerare la loro decomposizione in componenti associate alla decomposizione della rappresentazione regolare di quel gruppo. Più in generale, non è necessario supporre che le funzioni a quadrato sommabile siano definite su un gruppo, ma soltanto su di uno spazio S sul quale agisce un gruppo G e al quale è assegnata una misura G invariante μ. L'analisi armonica di un elemento di ℒ2(S, μ) consiste allora nella decomposizione della rappresentazione unitaria V di G definita ponendo Vx(f)(s) = f(sx) per tutti gli x in G e f in ℒ2(S, μ). Se, per esempio, S è la superficie di una sfera con raggio unità e centro nell'origine e G è il gruppo delle rotazioni intorno all'origine, V si decompone in sottospazi irriducibili di dimensione finita, uno per ogni dimensione dispari. Le funzioni in questi sottospazi di ℒ2(S, μ) sono le classiche armoniche sferiche.
Questo legame fra analisi di Fourier e teoria dei gruppi divenne ovvio non appena la teoria delle rappresentazioni dei gruppi venne estesa, intorno al 1920, da F. H. Schur, Peter e Weyl, ai gruppi compatti e ne vennero studiati i primi esempi. Tuttavia questo legame non fu rilevato prima, sebbene quella che oggi si può chiamare l'analisi di Fourier sui gruppi commutativi finiti fosse usata nella teoria dei numeri fin dall'inizio del XIX secolo (v. sopra, cap. 13). Inoltre, l'estensione ai gruppi non compatti dovette attendere ulteriori sviluppi della teoria delle rappresentazioni dei gruppi; l'inclusione delle trasformazioni di Fourier e delle serie di Fourier in una teoria generale fu effettuata per la prima volta da Weil nel suo libro del 1938 come applicazione della teoria della dualità di Pontrjagin e van Kampen.
Quando si studiano gruppi localmente compatti che non sono compatti, restringersi a funzioni a quadrato sommabile è relativamente impegnativo; ciò è vero, in particolare, quando il gruppo è il gruppo additivo della retta reale. La teoria di H. Bohr delle ‛funzioni quasi periodiche', pubblicata verso la metà del 1920, e quella di Wiener sull'‛analisi armonica generalizzata', del 1930, erano entrambe intese a estendere l'analisi armonica a funzioni non a quadrato sommabile sulla retta, ma tutte e due possono essere comprese mediante la decomposizione delle rappresentazioni del gruppo unitario ed estese a gruppi più generali. Secondo la definizione di Bochner, una funzione quasi periodica sulla retta è una funzione continua limitata, a valori complessi, le cui traslate hanno una chiusura compatta rispetto alla topologia della convergenza uniforme. Questa definizione ha senso per gruppi topologici arbitrari, ma, come fu per la prima volta segnalato da Weil nel 1935, le funzioni quasi periodiche su un gruppo topologico G sono precisamente le funzioni x ???14??? f(h(x)) ove h è un omomorfismo continuo canonico di G su un sottogruppo denso di un gruppo compatto K, definito in modo naturale, e f varia fra le funzioni continue su K. Questa circostanza riduce l'analisi armonica delle funzioni quasi periodiche a quella delle funzioni continue su un gruppo compatto. Introducendo delle nozioni di teoria ergodica, si può meglio comprendere la teoria di Wiener. Sia G il gruppo additivo della retta reale e sia S, C un G-spazio di misura propriamente ergodico (v. sopra, cap. 11). Supponiamo che C contenga una misura invariante μ (necessariamente unica), tale che μ(S) = 1, e sia f in ℒ2(S, μ). Per ogni x in S, s ???14??? f(sx)f(s) sta in ℒ1(S, μ) e, dal teorema ergodico, segue che
esiste per tutti gli s ed è uguale a
ove V è la rappresentazione unitaria di G definita da Vx(g) = g(sx) per g ∈ ℒ2(S, μ). Questo significa che, per quasi tutti gli s, la funzione y ???14??? f(sy) = fs(y) ha la proprietà che
esiste ed è uguale a (Vx(f)•f). Wiener si occupò soprattutto della classe di funzioni su G per le quali questo limite esiste ed è continuo. La sua analisi armonica di queste funzioni coincide essenzialmente con l'analisi delle funzioni fs che si ottengono decomponendo f secondo la decomposizione di V in rappresentazioni irriducibili. Nel caso speciale in cui V è una somma diretta discreta di rappresentazioni irriducibili e f è un sottospazio denso di ℒ2(S, μ), opportunamente definito, le funzioni fs sono quasi periodiche e l'analisi di Wiener si riduce a quella di H. Bohr.
Sia ora G un arbitrario gruppo separabile localmente compatto, sia S, C un G-spazio di misura tale che C contenga una misura invariante μ e sia V la rappresentazione associata del gruppo G, definita precedentemente. Se S = S1 ⋃ S2 ⋃ S3 ⋃ ..., ove gli Sj sono insiemi di Borel disgiunti che sono invarianti e hanno misura positiva, corrispondentemente V è una somma diretta delle sue restrizioni ai sottospazi di ℒ2(S, μ) costituiti dalle funzioni che si annullano fuori dagli Sj. Più in generale, la decomposizione canonica di S, C come somma diretta o integrale di componenti ergodiche si riflette in una corrispondente somma diretta o decomposizione integrale di V. Così ‛l'analisi armonica' delle funzioni su S può essere parzialmente sviluppata esaminando la ‛geometria' dell'azione di G su S. Di fatto, questa parte dell'analisi non è assolutamente considerata come analisi armonica. L'analisi armonica si occupa propriamente dell'ulteriore decomposizione delle rappresentazioni associate alle componenti ergodiche e quindi del caso speciale in cui l'azione di G è ergodica. Come abbiamo spiegato nel cap. 11, il caso ergodico si divide in due sottocasi piuttosto diversi fra di loro: quello in cui l'azione è propriamente ergodica e quello in cui l'azione è essenzialmente transitiva. Il caso propriamente ergodico è stato studiato sostanzialmente nel contesto della teoria ergodica e nell'applicazione di essa alla teoria della probabilità. Ben poco è stato fatto, a eccezione che per il gruppo additivo della retta reale o degli interi. Nel caso essenzialmente transitivo si può senz'altro supporre la transitività e identificare S con lo spazio quoziente G/H di un sottogruppo chiuso H di G; questo è il contesto più importante in cui ai giorni nostri si studia l'analisi armonica, più generale della teoria delle serie e degli integrali di Fourier. La rappresentazione V in questo caso non è altro che la rappresentazione di a indotta dalla rappresentazione banale a una dimensione di H e ci si chiede se le rappresentazioni di G indotte da altre rappresentazioni unitarie di H siano collegate in modo consimile a qualche altra generalizzazione dell'analisi armonica. La risposta è affermativa. Basta semplicemente sostituire le funzioni a valori complessi su S = G/H con funzioni a valori vettoriali, ove lo spazio vettoriale è uno spazio di Hilbert Hs che varia da punto a punto. Le funzioni a valori complessi sono cioè sostituite da ‛sezioni' di una ‛struttura fibrata'. Si suppone che G agisca sulla struttura fibrata in modo coerente con la sua azione su S, così che Hs è applicato in modo unitario su Hsx. La situazione è illustrata chiaramente dal caso in cui S è la superficie della sfera unità nello spazio e G è il gruppo delle rotazioni, come abbiamo già detto sopra. I piani tangenti ai punti di S sono spazi di Hilbert (reali) in modo naturale e ogni x in G definisce un isomorfismo del piano tangente nel punto s su quello tangente nel punto sx. Con queste estensioni a ‛campi di vettori' o a ‛sezioni di strutture fibrate', l'analisi armonica si identifica (almeno per quello che riguarda funzioni a quadrato sommabile) con la teoria della struttura delle rappresentazioni indotte. Quando si rifletta su questo fatto e sulla potenza e ubiquità dell'analisi di Fourier nella matematica classica e nella fisica, si può prevedere che problemi più sofisticati in questi campi risulteranno dipendere in modo essenziale dalla struttura delle rappresentazioni indotte. Nei capitoli successivi non mancheremo di dare degli esempi pertinenti.
Supponiamo che G sia unimodulare e di tipo I e sia H = {e}, cosicché S = G e la rappresentazione unitaria che dobbiamo decomporre è la rappresentazione regolare. In questo caso (come abbiamo spiegato nel cap. 8) l'analisi armonica associata non si limita a trovare la decomposizione in termini astratti. La classe di misure importante in Ø contiene un solo elemento ???42??? tale che, per ogni f in un opportuno sottospazio denso di ℒ2(G, μ), si ha
La misura ???42??? si chiama misura di Plancherel e la sua determinazione è una parte importante dell'analisi armonica di ℒ2(G, μ). Si può pensare a f ???14??? f(e) come al carattere della rappresentazione regolare di G e a f ???14??? Traccia (Lxf(x)) dμ(x) come al carattere della rappresentazione unitaria irriducibile L. Pertanto la formula di Plancherel dà la decomposizione della rappresentazione regolare in funzione dei caratteri delle rappresentazioni che in essa appaiono. Più in generale, sia H chiuso e unimodulare e sia M una rappresentazione unitaria di dimensione finita di H avente carattere χM. Se ν è una misura di Haar in H, il funzionale lineare
dipende soltanto dalla classe laterale destra di H che contiene y. Se infatti ???46???M è il sottogruppo del normalizzatore di H in G, costituito da tutti gli y per i quali χM(yxy-1) ≡ χM(x) e ν(yEy-1) ≡ ν(E), ly dipende soltanto dalla classe laterale destra ???46???M alla quale y appartiene e G/???46???M ammetterà una misura invariante ω. Il funzionale lineare
può essere considerato come il carattere della rappresentazione indotta Um e, si può cercare di esprimerlo come un integrale del tipo
∫ [Traccia ∫ Lxf(x) dμ(x)] dα(L),
dove α è una misura in Ø. La misura α, ammesso che esista e che sia unica, prende il nome di ‛misura di Plancherel' della rappresentazione indotta UM. Naturalmente, quando H = {e} e M è la rappresentazione banale di dimensione 1 di H, ???46???M = G e ly(f) = f(e), cosicché la misura di Plancherel per la rappresentazione regolare risulta un caso speciale. Quando G è commutativo e M è l'identità a una dimensione, risulta
e
Traccia ∫ Lxf(x) dμ(x) = ???43???(L)
e α è una misura di Haar in H⊥, ‛l'annullatore' di H nel gruppo dei caratteri Ø di G. La formula di Plancherel in questo caso non è altro che la formula sommatoria di Poisson le cui numerose applicazioni alla teoria dei numeri sono state brevemente descritte nel capitolo precedente. Uno dei maggiori contributi del lavoro di Selberg del 1956, che abbiamo ricordato alla fine di tale capitolo, è una formula nota come la ‛formula della traccia di Selberg', la quale ha anch'essa numerose conseguenze nella teoria dei numeri. Selberg la presenta come una generalizzazione della formula sommatoria di Poisson e infatti essa è essenzialmente la formula di Plancherel sopra descritta per il caso particolare in cui G è un gruppo di Lie semisemplice e H è un sottogruppo chiuso numerabile con uno spazio quoziente compatto.
Un caso speciale, che ha suscitato particolare attenzione, è quello in cui S è uno ‛spazio simmetrico' nel senso di Cartan e G è un gruppo di Lie transitivo di isometrie. Si può considerare S come un analogo a più dimensioni, eventualmente ‛curvo', dello spazio euclideo ordinario, uno spazio, cioè, sul quale è definita una ‛geometria non euclidea' omogenea. Scartando eventuali ‛componenti piatte' e certe altre eccezioni, questo caso coincide con quello in cui S = G/K, ove G è un gruppo di Lie connesso semisemplice e K è un sottogruppo compatto massimale. Come fu osservato per la prima volta da I. M. Gelfand nel 1950, l'analisi armonica delle funzioni scalari è in questo caso notevolmente favorita dal fatto che la rappresentazione unitaria UIK di G, indotta dalla rappresentazione banale IK di K, ha un'algebra commutante commutativa ed è pertanto ‛priva di molteplicità' (v. sopra, cap. 8). Le rappresentazioni unitarie irriducibili di G, necessarie per decomporre UIK, comprendono esattamente quelle che contengono l'identità quando si restringano a K; queste rappresentazioni si dimostrano molto più facili da studiare degli elementi della classe più ampia, necessari per decomporre le rappresentazioni regolari. In particolare, esse sono tutte indotte da rappresentazioni di dimensione finita del gruppo NAM cui abbiamo accennato nel cap. 8. Harish-Chandra ha ottenuto la corrispondente misura di Plancherel nel 1958, alcuni anni prima di riuscire a trattare la molto più complessa rappresentazione regolare.
Quando V e W sono rappresentazioni unitarie di struttura nota, è facile trovare tutti i possibili operatori d'intrecciamento per V e W; inversamente, si può determinare la struttura di V se si ha una conoscenza sufficiente degli operatori d'intrecciamento per V e una certa rappresentazione W, la cui struttura sia nota. Ciò accade perché l'operatore d'intrecciamento definisce un'equivalenza fra una sottorappresentazione di V e una di W (v. sopra, cap. 8). Siano ora V e W due rappresentazioni indotte UL e UM, ove L e M sono rispettivamente due rappresentazioni unitarie di dimensione finita di sottogruppi chiusi H1 e H2. In questo caso è spesso possibile scrivere esplicitamente gli operatori d'intrecciamento per V e W quando siano note soltanto le rappresentazioni inducenti L e M. In tal modo è possibile acquisire informazioni sulla struttura di V a partire da fatti noti su W. L'idea direttrice è che, quando G è un gruppo finito, si può facilmente scrivere l'operatore d'intrecciamento più generale. Questi operatori corrispondono biunivocamente alle funzioni A da G allo spazio vettoriale di tutti gli operatori lineari da ℋ(L) a ℋ(M) che soddisfano l'identità A(ξxη = LξA(x)Mη per tutti gli ξ in H1 e tutti gli η in H2. Una funzione soddisfacente questa identità è univocamente determinata, su ogni classe laterale doppia H1 : H2 di H1 × H2, dal suo valore in x ed è univocamente una somma di funzioni che soddisfano l'identità e sono nulle tranne che su una classe laterale doppia. La costruzione dell'operatore d'intrecciamento associato alla funzione A avente un dato valore nel punto x0 e nulla fuori di H1x0H2 (e univocamente determinata da queste condizioni) può servire come modello formale anche quando G non è finito. Se certi integrali convergono, questo procedimento fornisce un operatore d'intrecciamento, che verrà chiamato ‛operatore d'intrecciamento per una classe laterale doppia'. Nel caso particolare in cui L e M sono entrambi banali e G/H1 e G/H2 ammettono ambedue misure invarianti, gli operatori già esistenti di classi laterali doppie assumono la forma f ???14??? f′, ove f′(s2) = ∫ f(s1) dνs2 • (s1) e s2 ???14??? νs2 fa corrispondere una misura su S1 = G/H1 a ogni s2 in S2 = G/H2. Quando G è il gruppo generato dalle traslazioni e rotazioni in uno spazio euclideo a n dimensioni, quando H1 è il sottogruppo di tutte le rotazioni attorno a un dato punto fisso e H2 è il sottogruppo che lascia invariante un prefissato iperpiano a n − 1 dimensioni, si può identificare G/H1 con lo spazio euclideo e G/H2 con tutti gli iperpiani a n − 1 dimensioni. L'operatore d'intrecciamento per le classi laterali doppie definito dalla funzione che è 1 in e e 0 fuori di H1 : H2 è la cosiddetta ‛trasformazione di Radon', la quale trasforma funzioni opportunamente ristrette su uno spazio euclideo in funzioni sugli iperpiani a n − 1 dimensioni, il cui valore, su un qualsiasi iperpiano, è l'integrale di f sull'iperpiano stesso. Sostituendo lo spazio euclideo con uno spazio simmetrico G/K, ove K è il sottogruppo massimale compatto di un gruppo di Lie semisemplice G, si ottiene un analogo della trasformazione di Radon, prendendo H1 = K e H2 = NA, ove G = NAK è una decomposizione di Iwasawa (v. sopra, cap. 6). Gli analoghi degli iperpiani a n − 1 dimensioni sono le orbite in G/K dei coniugati di H2 = NA e sono quelli che Gelfand chiama ‛orosfere'. Il metodo ‛orosferico', mediante il quale Gelfand e Graev hanno determinato la struttura di UIK, non è altro che il metodo generale descritto precedentemente, quando si usi UIH2 come rappresentazione indotta di struttura nota. Uno studio molto dettagliato della trasformazione di Radon in spazi simmetrici generali è stato portato a termine da Helgason.
Molti altri operatori che sono stati oggetto di studi speciali in vari rami della matematica risultano essere casi particolari di operatori d'intrecciamento di classi laterali doppie - uno di questi è l'operatore definito dal nucleo di Poisson della teoria del potenziale. Altri esempi verranno ricordati nei capitoli che seguiranno. Più in generale, molti sono gli oggetti nella matematica e nella fisica che possono essere identificati con gli operatori d'intreccia- mento per due rappresentazioni indotte e analizzati secondo i metodi dell'analisi armonica.
15. Teoria dei gruppi e teoria delle funzioni di una variabile complessa.
Dopo l'invenzione, dovuta a Newton e Leibniz nel XVII secolo, del calcolo differenziale e integrale, uno dei maggiori problemi dei matematici divenne lo studio delle nuove funzioni trascendenti che si presentano quando s'integrano quelle funzioni elementari che non sono derivate di altre funzioni elementari. Così come si ha (d/dx) log x = 1/x, onde si deve introdurre la funzione trascendente log x per integrare la funzione razionale 1/x, analogamente la funzione algebrica elementare
(con k2 ≠ 1) non può essere integrata senza introdurre funzioni di tipo nuovo e completamente diverso. Quest'ultimo problema d'integrazione sorge quando si cerca di determinare la lunghezza di un arco di un'ellisse; corrispondentemente, le nuove funzioni trascendenti, al pari di altre a esse strettamente collegate, sono note come ‛integrali ellittici'. Le proprietà degli integrali ellittici furono oggetto di una indagine dettagliata soprattutto da parte di A.-M. Legendre, che dedicò gran parte della sua vita al loro studio e, nel 1826, pubblicò un ampio trattato sull'argomento. Tuttavia questo campo di ricerche venne completamente trasformato non appena si scopri come queste funzioni si comportano quando le variabili possono assumere valori complessi e non solo valori reali. Si scoprì che queste funzioni possono essere univocamente estese dalla retta reale al piano complesso in modo da risultare funzioni ‛analitiche' o ‛olomorfe' a eccezione di ‛singolarità' isolate. Si dice che una funzione a valori complessi f definita su un sottoinsieme aperto ℴ del piano complesso è ‛analitica' o ‛olomorfa' in ℴ se, per ogni z0 in ℴ, esiste un numero complesso f′(z0) tale che
può essere reso piccolo a piacere, a condizione di prendere z abbastanza vicino a z0. La funzione z ???14??? f′(z) prende il nome di derivata di f. La sua esistenza è una condizione molto più restrittiva dell'esistenza della derivata per una funzione di variabile reale. Di fatto, f′ risulta essere essa stessa necessariamente analitica, cosicché esistono f″ = (f′)′, f‴ = (f″)′, ecc. Si può dimostrare inoltre che due funzioni analitiche, che coincidono su un segmento arbitrariamente piccòlo e sono analitiche in un insieme aperto connesso contenente tale segmento, coincidono in tutto l'insieme aperto. Se f è analitica nell'insieme aperto ℴ, a eccezione che nel punto z0 contenuto in ℴ, e f(z) tende a ∞ quando z tende a z0, si dice che z0 è un ‛polo' della funzione f. Esiste uno e un solo numero intero positivo k e una e una sola funzione g analitica in ℴ, tale che g(z0) ≠ 0 e
per z in ℴ − {z0}. L'intero positivo k prende il nome di ‛ordine' del polo. Una funzione analitica in un insieme aperto a eccezione di poli si dice ‛meromorfa'. L'analogo della proprietà
sta nel fatto che
preso come integrale curvilineo su un'arbitraria curva (di lunghezza finita) congiungente z0 e z, è largamente indipendente dalla curva stessa e definisce una funzione analitica z la cui derivata è f. Questa indipendenza è una conseguenza di un famoso teorema di Cauchy la cui pubblicazione, avvenuta nel 1825, può considerarsi l'atto di nascita della teoria delle funzioni di una variabile complessa. Questo teorema afferma che se C è una curva chiusa, risulta
ogniqualvolta f è analitica in C e in tutti i punti ‛interni' a C. Un importante corollario di questo teorema è che, quando f è analitica in C e su C, eccetto che per un numero finito di poli del primo ordine nei punti z1, z2, ..., zn, risulta
ove Rj - residuo di f in zj - è
(L'estensione a poli di ordine superiore e a ‛singolarità essenziali' fu scoperta più tardi). Come venne dimostrato da Cauchy, questo corollario può essere usato come efficace strumento per calcolare integrali definiti.
Ancora più importante, nella dimostrazione dell'utilità dell'estensione al piano complesso, fu un'osservazione, fatta indipendentemente da Abel e da Jacobi fra il 1826 e il 1829, secondo la quale l'inverso di un integrale ellittico, considerato come funzione di una variabile complessa, è periodico con due periodi ‛indipendenti' complessi. Così come lo studio delle funzioni periodiche sen x e cos x è più facile di quello delle loro funzioni inverse, le funzioni doppiamente periodiche inverse degli integrali ellittici hanno una teoria molto più elegante che gli integrali ellittici. Dopo la pubblicazione del lavoro fondamentale di Jacobi del 1829 su questo argomento, l'attenzione si concentrò sullo studio di quegli inversi detti funzioni ellittiche. Più in generale, una funzione ellittica è per definizione una funzione f, meromorfa in tutto il piano complesso, che è ‛doppiamente periodica', nel senso che il gruppo additivo di tutti gli ω per i quali f(z + ω) = f(z), per ogni z, è un sottogruppo discreto a quoziente compatto del gruppo additivo di tutti i numeri complessi. Non è difficile mostrare che il sottogruppo più generale di questo tipo è proprio l'insieme dei numeri complessi del tipo nω1 + mω2, ove ω1 e ω2 sono prefissati numeri non nulli tali che ω1/ω2 non è reale e n e m sono interi. I numeri complessi ω1 e ω2 prendono il nome di ‛periodi primitivi' delle funzioni ellittiche associate e il parallelogramma con vertici 0, ω1, ω2 e ω1 + ω2 viene chiamato ‛parallelogramma dei periodi'. Ovviamente una funzione ellittica è completamente determinata dal suo andamento nel parallelogramma dei periodi e può avere in esso soltanto un numero finito di poli e di zeri. Se si assume per definizione come ordine di uno zero l'ordine del corrispondente polo di 1/f]; si può dimostrare che una funzione ellittica è determinata, a meno di una costante moltiplicativa, dai suoi zeri, dai suoi poli e dagli ordini di essi. Poiché è possibile dare condizioni necessarie e sufficienti per l'esistenza di una funzione ellittica avente dati zeri e dati poli di un ordine fissato, si può dire di avere una visione completa di tutte le possibili funzioni ellittiche.
Abel e Jacobi affrontarono il difficile studio degli integrali di funzioni algebriche più generali. Tale studio fu portato a termine in modo più o meno completo da B. Riemann e K. Weierstrass nel periodo fra il 1850 e il 1860. Non sarà difficile descrivere in seguito l'opera di Abel Jacobi, ispirato dalle ricerche di Abel, mostrò, nel 1832-1834, come fosse possibile generalizzare la doppia periodicità della funzione inversa di un integrale ellittico. Nel caso particolare trattato da Jacobi, si hanno due integrandi f1 e f2 e si considera la funzione
che, essendo invariante rispetto alla trasformazione z1, z2 ???14??? z2, z1, può essere considerata come funzione di z1 + z2 e z1z2. L'inversa di quest'ultima funzione risulta essere una funzione a quattro periodi delle due variabili complesse w1 e w2. Nel caso generale trattato da Riemann e Weierstrass, si hanno p integrandi (p essendo un intero positivo arbitrario) e, dopo aver sostituito a z1, z2, ..., zp opportune combinazioni simmetriche delle variabili, si scopre che la funzione inversa dipende da p variabili complesse con 2p periodi indipendenti. Il significato di p può essere meglio compreso, al pari di altri aspetti della teoria, ricorrendo al ricoprimento a più fogli del piano complesso, introdotto nel 1857 da Riemann e che porta ora il nome di ‛superficie di Riemann'. Le funzioni algebriche di cui si vogliono calcolare gli integrali risultano essere di solito, in modo naturale, ‛multivoche' e Riemann mostrò come tale multivocità possa essere ridotta a univocità, in modo utile e coerente, introducendo tante copie del piano complesso quanti sono i valori e operando certe modificazioni in modo da saldare le differenti copie (fogli) in un unico spazio topologico connesso. S'introduce poi il ‛punto all'infinito' su ciascun foglio, ottenendo così uno spazio topologico compatto, che è una ‛superficie' nel senso che ciascun suo punto ha un intorno omeomorfo all'interno del disco unità. L'intero p risulta essere un invariante topologico della superficie, che Riemann considerò come una misura del grado di connessione e definì come risultato di un certo numero di ‛retrosezioni'. Nella teoria generale iniziata da Poincaré, p è il primo numero di Betti. Esso viene chiamato il ‛genere' della superficie di Riemann e risulta uguale anche alla dimensione dello spazio vettoriale complesso dei ‛differenziali' f(z) dz, definiti sulla superficie e olomorfi ovunque. Gli elementi di una qualsiasi base di questo spazio possono essere presi come i p integrandi necessari alla formazione del teorema generalizzato di inversione di Jacobi. Procedendo in modo più astratto, come si usa oggi, non si sceglie affatto una base, ma si prende una qualsiasi curva γ di lunghezza finita e a partire da essa si definisce un funzionale lineare lγ sullo spazio dei differenziali olomorfi:
lγ(f dz) = ∫γ f dz.
Le somme e le differenze degli lγ, quando γ è ‛chiusa', si chiamano ‛periodi' e formano un sottogruppo discreto Γ, con quoziente compatto, del gruppo additivo dello spazio vettoriale V- , duale dello spazio vettoriale V dei differenziali olomorfi. Il gruppo quoziente corrispondente V- /Γ è un gruppo di Lie compatto e commutativo associato in modo intrinseco alla superficie di Riemann ℛ. L'algebra di Lie di V- /Γ si può identificare con lo spazio vettoriale reale soggiacente allo spazio vettoriale complesso V- , cosicché questa algebra di Lie ammette una moltiplicazione canonica per i. Il gruppo di Lie compatto V- /Γ con questa struttura addizionale prende il nome di ‛varietà di Jacobi' di ℛ. Il teorema di Abel, al quale abbiamo precedentemente accennato, può essere riformulato come condizione necessaria e sufficiente per l'esistenza di una funzione meromorfa avente su ℛ dati zeri e dati poli di ordine assegnato. Nel caso particolare in cui p = 1, si può identificare ℛ con V- /Γ (dopo aver scelto un arbitrario punto di partenza p0) e la teoria delle funzioni meromorfe su ℛ coincide con la teoria di quelle funzioni ellittiche su V- aventi Γ come gruppo dei periodi. In questo caso, naturalmente, V- ha dimensione 1 e può essere identificato con il piano complesso.
Quando p > 1, V- /Γ diventa qualcosa di diverso daℛ e lo studio delle funzioni su-esso definite è equivalente (una volta fissata una base per V- ) allo studio delle funzioni di p variabili complesse aventi 2p periodi. La nozione di funzione analitica può essere estesa, in modo più o meno ovvio, al caso di funzioni di più variabili complesse e si scopre che il fatto che una funzione su V- sia analitica come funzione di p variabili complesse è indipendente dalla scelta della base. Si dice che una funzione su un sottoinsieme aperto ℴ di V- è meromorfa quando essa è il quoziente di due funzioni analitiche in un intorno aperto di ogni punto di ℴ. Le funzioni meromorfe su V- , costanti sulle classi laterali di Γ, costituiscono una generalizzazione naturale delle funzioni ellittiche e nascono, come abbiamo indicato dianzi, quando s'invertono i sistemi di integrali su ℛ Esse prendono il nome di funzioni abeliane e le loro proprietà furono oggetto di uno studio sistematico da parte di Riemann e Weierstrass. Quest'ultimo fece infatti delle funzioni abeliane il motivo principaledelle sue ricerche e nel portare avanti questo programma fece compiere grandi progressi, anche sul piano del rigore critico, alla teoria generale delle funzioni di una o più variabili complesse. Nel 1831 A.-L. Cauchy dimostrò il teorema fondamentale secondo cui una funzione di una variabile complessa è analitica se, e soltanto se, per ciascun punto z0 del suo dominio di definizione esiste una serie di potenze assolutamente convergente a0 + a1(z − z0) + ..., la cui somma è uguale al valore della funzione per tutti gli z sufficientemente vicini a z0. Un fatto simile vale per le funzioni di più variabili complesse e Weierstrass adottò il punto di vista secondo cui una funzione analitica è definita da una famiglia di serie di potenze convergenti che sono il ‛prolungamento' l'una dell'altra. Se Γ0 è un arbitrario sottogruppo discreto a quoziente compatto di uno spazio vettoriale complesso W, la coppia W, Γ0 non è necessariamente isomorfa alla coppia V- , Γ che nasce dalla superficie di Riemann ℛ di una certa funzione algebrica, ma, anche in questo caso, si possono studiare le funzioni abeliane su W (o W/Γ0). Weierstrass si dedicò anche allo studio di queste funziorn abeliane più generali. Può accadere che esse siano tutte costanti, ma, se ne esistono a sufficienza da separare i punti di W/Γ0, si dice che W/Γ0 è una ‛varietà abeliana'. Segue facilmente dalla compattezza di W/Γ0 che le funzioni analitiche su tutto W e costanti sulle classi laterali di Γ0 sono necessariamente costanti su tutto W. Le funzioni abeliane, quando esistono, si costruiscono come quozienti di funzioni note come ‛funzioni theta'. Queste sono funzioni analitiche f su W tali che, per tutte le γ in Γ0, w ???14??? f(w + y)/f(w) è del tipo w ???14??? ePγ(w), ove Pγ è un polinomio di secondo grado in w. I teoremi che riguardano l'esistenza e le proprietà delle funzioni theta sostengono un ruolo fondamentale nella teoria delle funzioni abeliane. Molti dei risultati attribuiti dianzi a Cauchy, Jacobi, Abel ecc. furono scoperti indipendentemente da Gauss che li aveva annotati sui suoi quaderni non pubblicati.
L'esame dei valori complessi della variabile si rivela utile non solo quando s'integrano funzioni algebriche, ma anche quando si risolvono equazioni differenziali a coefficienti algebrici. Si consideri l'equazione lineare del secondo ordine
Si vede facilmente che la sua soluzione generale è
dove c1 e c2 sono costanti arbitrarie e g è il quoziente di due soluzioni linearmente indipendenti qualsiasi. D'altra parte, se g-1 esiste come funzione univoca, si può dimostrare che
per tutte le matrici
in un sottogruppo numerabile Γ del gruppo SL(2, C) di tutte le matrici complesse 2 × 2 di determinante 1. Pertanto, come un integrale ellittico è l'inverso di una funzione che è invariante rispetto al sottogruppo commutativo discreto Γ(ω1, ω2) di SL(2, C), costituito da tutte le matrici
con a = d = 1, c = 0 e b = nω1 + mω2 (con m e n interi), così le soluzioni di certe equazioni differenziali del secondo ordine possono essere espresse semplicemente mediante l'inversa di una funzione invariante rispetto a un sottogruppo numerabile Γ di SL(2, C) non necessariamente commutativo. Pare sia stato H. A. Schwarz nel 1872 il primo a rilevare questo fatto nel caso particolare della così detta equazione differenziale ‛ipergeometrica', sebbene già Riemann avesse aperto la strada nel 1857 con il suo famoso lavoro sull'equazione in questione. Per opportuni valori delle costanti arbitrarie in questa equazione, Schwarz poté dimostrare non solo che g-1 è univoca, ma che esiste un analogo del parallelogramma dei periodi della teoria delle funzioni ellittiche. Si può trovare un triangolo, i cui lati sono archi circolari, dotato della proprietà che i suoi trasformati mediante Γ coprono il piano complesso in modo tale che due trasformati distinti non si sovrappongono se non su un lato. Un po' più tardi, nel 1880, I. L. Fuchs estese i risultati di Schwarz a equazioni più generali usando poligoni in luogo di triangoli. Queste ricerche di Fuchs convinsero Poincaré (che aveva allora soltanto 26 anni) ad affrontare il seguente problema di carattere generale. Per quali sottogruppi numerabili Γ di SL(2, C) esistono funzioni meromorfe f che sono invarianti rispetto a Γ? Inoltre, come è possibile costruire la più generale ditali funzioni? Altri casi speciali erano stati in precedenza esaminati da F. Klein per scopi diversi; in particolare quelli in cui Γ è finito oppure è il ‛gruppo modulare' di tutte le matrici in SL(2, C) a coefficienti interi. Klein e Poincaré si misero in corrispondenza epistolare e l'unione dei loro sforzi portò alla creazione di una vasta teoria, che è nota ora come teoria delle ‛funzioni automorfe'. Essa portò la teoria dei gruppi a interagire in modo profondo con la teoria delle funzioni analitiche; risulta così che le funzioni meromorfe su una superficie di Riemann arbitraria possono essere identificate con le funzioni automorfe rispetto a un opportuno sottogruppo numerabile Γ di SL(2, C) e la classificazione delle superfici di Riemann si può ridurre alla classificazione di questi sottogruppi. Questo enunciato, inoltre, vale non solo per le superfici di Riemann compatte che nascono dalla teoria degli integrali di una funzione algebrica, ma anche per le più generali superfici di Riemann ‛astratte' che vennero introdotte più tardi. Sia ℛ uno spazio topologico connesso e, in corrispondenza con ogni insieme aperto ℴ di ℛ, sia assegnata una famiglia ℱℴ di funzioni continue a valori complessi. Si dice che ℛ è una ‛varietà complessa a n dimensioni' rispetto alla famiglia assegnata quando valgono le seguenti condizioni: 1) se f è definito in ℴ e se per ogni punto p in ℴ esiste un insieme aperto più piccolo, ℴ′, contenente p e tale che f coincida in ℴ′ con una certa g in ℱℴ, allora f sta in ℱℴ; 2) per ogni p in ℛ e per ogni insieme aperto ℴ contenente p, esiste un insieme aperto più piccolo, ℴ′, contenente p e un omeomorfismo ϕ di ℴ′ nell'insieme delle n-uple di numeri complessi con ∣ z1 ∣2 + ... + ∣ zn ∣2 〈 1, in modo tale che f sta in ℱℴ′ se e soltanto se z1, ..., zn ???14??? f(ϕ-1(z1, ..., zn)) è una funzione analitica. Una ‛superficie di Riemann' (astratta) è semplicemente una varietà complessa a una dimensione. Un omeomorfismo ϕ di una varietà complessa ℛ1 su una varietà complessa ℛ2 si dice ‛isomorfismo di varietà complessa', oppure si dice che esso conserva la ‛struttura complessa', se, per ogni insieme aperto ℴ di ℛ1, gli elementi di ℱ῍(ℴ) sono esattamente le funzioni p ???14??? f(ϕ-1(p)) al variare di f fra gli elementi di ℱℴ. Quando un tale ϕ esiste si dice che ℛ1 e ℛ2 sono varietà complesse isomorfe. Una funzione a valori complessi f su una varietà complessa ℛ si dice ‛meromorfa' se, per ogni punto p di ℛ, essa è il quoziente di due elementi di ℱℴ per un opportuno insieme aperto ℴ, contenente il punto p. Essa si dice ‛analitica' se il denominatore può sempre essere preso uguale a 1. Data una varietà complessa ℛ, se ne può considerare il rivestimento universale ???30??? e il gruppo fondamentale Γ, identificando ℛ con lo spazio delle Γ orbite in ???30???. Inoltre si può dare a ???30??? la struttura di varietà complessa in modo tale che le funzioni meromorfe su ℛ ‛rialzate' a funzioni su ???30??? siano precisamente le funzioni meromorfe su ℛ che sono Γ invarianti e tali che ciascun elemento di Γ è un automorfismo di ???30??? come varietà complessa. Nel caso particolare in cui ℛ ha dimensione 1, un teorema fondamentale afferma che ???30??? è isomorfa a una e una sola delle seguenti superfici di Riemann:1) il piano complesso; 2) il piano complesso con l'aggiunta di un punto all'infinito; 3) il ‛semipiano superiore', costituito dai numeri complessi con parte immaginaria positiva. Corrispondentemente si dice che la superficie di Riemann è parabolica, ellittica o iperbolica. Nel caso iperbolico si dimostra che l'automorfismo più generale di ???30??? è la trasformazione
ove ad − bc = 1 e a, b, c e d sono numeri reali. Pertanto le funzioni meromorfe su una arbitraria superficie di Riemann iperbolica possono essere identificate con le funzioni meromorfe sul semipiano superiore che sono automorfe rispetto a un sottogruppo numerabile chiuso Γ di SL(2, R). Risultati simili valgono per superfici di Riemann ellittiche e paraboliche. Due superfici di Riemann compatte sono omeomorfe se, e soltanto se, esse hanno lo stesso genere p. Esiste tuttavia un continuo di superfici di Riemann compatte non isomorfe per ciascun valore del genere p ≥ 1. Poiché superfici di Riemann omeomorfe hanno gruppi fondamentali isomorfi, il problema di trovare tutte le superfici di Riemann iperboliche di un dato genere p non isomorfe è equivalente al problema di pura teoria dei gruppi, che consiste nell'analizzare tutti i possibili isomorfismi di un gruppo numerabile Γ di data struttura in SL(2, R). Questo problema non è lontano dallo studio delle classi di equivalenza delle rappresentazioni reali a due dimensioni di Γ, ma differisce da esso in due aspetti. Non solo certe rappresentazioni devono venire escluse, ma rappresentazioni non equivalenti possono definire superfici di Riemann isomorfe. D'altra parte, lo spazio delle classi di equivalenza di quelle rappresentazioni bidimensionali di Γ che corrispondono a superfici di Riemann compatte di genere p è un cosiddetto ‛spazio di rivestimento' dello spazio delle classi di isomorfismo delle superfici; tale spazio, che si è rivelato di notevole importanza, prende il nome di spazio di Teichmüller.
Una varietà abeliana può essere definita equivalentemente come un gruppo di Lie compatto commutativo che è anche una varietà complessa, tale che le traslazioni del gruppo siano automorfismi complessi. La varietà ???30??? in tal caso è uno spazio vettoriale complesso a n dimensioni e il gruppo fondamentale Γ è il gruppo dei periodi. L'analogia tra funzioni abeliane e funzioni automorfe, alla quale abbiamo accennato dianzi, risulta essere assai profonda. In particolare le funzioni automorfe possono essere ottenute come quozienti di certe funzioni analitiche ovunque che sono le analoghe delle funzioni theta e vengono chiamate ‛forme automorfe'. Di solito ci si interessa a quelle forme automorfe che non solo sono analitiche ovunque, ma che soddisfano anche a certe condizioni di limitatezza. In tutta generalità, una forma ‛automorfa' di ‛peso' k (intero) rispetto al sottogruppo chiuso numerabile Γ di SL(2, R) è, per definizione, una funzione meromorfa definita su un aperto Γ invariante del piano complesso (con l'aggiunta di ∞) che soddisfa l'identità
per tutte le
in Γ. A prima vista quest'identità può sembrare molto diversa da quella che definisce le funzioni theta, ma si può dimostrare che si tratta praticamente della stessa cosa. Secondo una nomenclatura leggermente diversa, ma anch'essa di uso comune, una forma di peso k si dice di ‛dimensione' −2k. Poincaré costruì forme automorfe modificando un metodo usato precedentemente per la costruzione di funzioni theta. Sia h una funzione meromorfa in un insieme aperto Γ invariante. La serie infinita
(estesa a tutte le
in Γ) non converge necessariamente. Se essa converge uniformemente sui sottoinsiemi compatti, la somma è ovviamente una forma automorfa (senza restrizioni sulla limitatezza) di peso k. Tali serie sono note come serie di Poincaré. Poincaré, inoltre, concentrò la sua attenzione sul problema di determinare i possibili sottogruppi discreti (cioè chiusi e numerabili) Γ di SL(2, C) e sul problema, strettamente connesso, di analizzare la struttura del piano complesso ⋃∞, considerato come un Γ-spazio. Per definizione un punto limite di un Γ-spazio è un punto che è limite di una successione di punti di tipo
ove le
sono elementi distinti di Γ. Se l'insieme aperto di tutti i punti che non sono punti limiti non è vuoto, il gruppo Γ si chiama gruppo di Klein; un gruppo di Klein coniugato a un sottogruppo di SL(2, R) si dice ‛fuchsiano'. Il caso fuchsiano è molto più facile e relativamente a esso Poincarè ottenne risultati completi. Il caso, più difficile, di grupPi di Klein che non sono fuchsiani è di grande interesse per le ricerche attuali. Nel caso fuchsiano si può considerare Γ, senza perdere generalità, come un sottogruppo di SL(2, R) operante sul semipiano superiore. Poincaré basò le sue ricerche sull'osservazione che si può considerare il semipiano superiore come lo spazio di una geometria ‛non euclidea' a due dimensioni il cui gruppo delle isometrie (transitivo) è per l'appunto SL(2, R) modulo i suoi due elementi centrali. In questo modo egli riuscì a dimostrare che, ogniqualvolta lo spazio delle orbite di Γ è compatto, esiste una ‛regione fondamentale' (cioè un analogo del parallelogramma dei periodi) i cui lati sono ‛rette non euclidee'. Inoltre egli riuscì a caratterizzare quei poligoni non euclidei che nascono in questo modo e a utilizzare le loro proprietà geometriche per classificare i corrispondenti gruppi fuchsiani.
Di particolare interesse per le applicazioni della teoria delle forme automorfe alla teoria dei numeri, ricordata nel cap. 13, è la classe speciale di gruppi fuchsiani costituita dai sottogruppi di indice finito di SL(2, Z), il gruppo delle matrici 2 × 2 con elementi interi e determinante 1. Il gruppo SL(2, Z) si chiama gruppo modulare e le forme automorfe rispetto ai suoi sottogruppi di indice finito si chiamano ‛forme modulari'. Fra questi sottogruppi di indice finito, hanno un ruolo speciale i cosiddetti ‛sottogruppi di congruenza principale'. Per ogni intero q, sia Γq l'insieme di tutte le
in SL(2, Z) tali che a − 1, b, c e d −1 siano divisibili per q. Γq risulta essere un sottogruppo normale di indice finito e prende il nome di ‛sottogruppo di congruenza principale di livello q'. Ogniqualvolta Γ è un sottogruppo di indice finito di SL(2, Z), la superficie di Riemann RΓ ottenuta dal semipiano superiore identificando i punti che stanno nella stessa Γ-orbita, non è compatta, ma può essere ‛compattificata' con l'aggiunta di un numero finito di punti. Corrispondentemente, una regione fondamentale per Γ nel semipiano superiore non può essere isolata dall'asse reale. La sua curva frontiera ha delle ‛cuspidi' sull'asse reale: una per ciascun punto che deve essere aggiunto per rendere compatta RΓ. Le forme modulari interessanti nella teoria dei numeri non sono soltanto analitiche ovunque, ma sono, in un certo senso, finite su ciascuna cuspide. Quelle che per di più si annullano su ciascuna cuspide vengono chiamate ‛forme cuspidali'. Le forme cuspidali costituiscono un sottospazio di dimensione finita dello spazio vettoriale di tutte le forme di un dato peso positivo che sono analitiche e finite sulle cuspidi. La dimensione dello spazio quoziente è uguale al numero delle cuspidi. Associata a ogni cuspide è una forma canonica modulare che si annulla ovunque tranne che su quella cuspide. Essa si costruisce mediante una serie di Poincaré modificata che prende il nome di ‛serie di Eisenstein'. Ovviamente, ogni forma analitica modulare è, in modo univoco, la somma di una forma cuspidale e di una combinazione lineare finita di serie di Eisenstein. Le cuspidi possono essere descritte, nel puro ambito della teoria dei gruppi, senza passare attraverso il dominio fondamentale. Da questo punto di vista esse corrispondono, in modo biunivoco, a certe classi laterali doppie di T: Γ, ove T è il sottogruppo di G = SL(2, R) costituito dalle matrici
in SL(2, R) con c = 0. Poiché T è il sottogruppo che lascia fisso ∞ nell'estensione naturale di SL(2, R) come gruppo operante sull'asse reale, lo spazio quoziente G/T si pùò identificare con l'asse reale; le classi laterali doppie di T: Γ corrispondono biunivocamente in modo naturale alle Γ-orbite sull'asse reale. T è il normalizzatore del sottogruppo N delle matrici
e si verifica facilmente che il fatto che Γ ⋂ x-1Nx contenga o no elementi diversi dall'identità e dipende soltanto dalla classe laterale doppia T × Γ. Le classi laterali doppie per le quali x-1Nx ⋂ Γ ≠ {e} corrispondono alle cuspidi. La classe laterale doppia che contiene e è sempre una cuspide ed è la sola quando Γ è l'intero gruppo modulare Γ0. Essa viene chiamata la cuspide all'infinito. La serie di Eisenstein corrispondente si ottiene trascurando dei termini nella serie di Poincaré
ottenuta ponendo h(z) ≡ 1. Poiché il contributo dato a questa somma da elementi nella stessa classe laterale di Γ ⋂ N sono uguali, la serie di Poincaré non può convergere. La serie di Eisenstein è ottenuta scegliendo un elemento da ogni classe laterale di Γ ⋂ N ed eliminando tutti i termini non associati a questi elementi. Le altre cuspidi sono trasformate della cuspide all'infinito mediante elementi dell'intero gruppo modulare e, corrispondentemente, le altre serie di Eisenstein sono trasformate della serie di Eisenstein per la cuspide all'infinito. Esse hanno tutte la forma
dove la somma è estesa a un opportuno sottoinsieme dell'intero gruppo modulare. Poiche Γ contiene elementi del tipo
con b ≠ 0, ogni forma modulare f per Γ è periodica con periodo b e ha uno sviluppo di Fourier
Inoltre, se f è finita nella cuspide all'infinito, si può dimostrare che ϕ(n) = 0 per n 〈 0, cosicché
Quando f è una serie di Eisenstein, si possono calcolare esplicitamente i coefficienti di Fourier ϕ(n) e, quando f è una forma cuspidale, si può dimostrare che i ϕ(n) sono ‛piccoli'. Da queste osservazioni si rileva come si possano ottenere espressioni asintotiche per le funzioni della teoria dei numeri n ???14??? ϕ(n), dimostrando che
è una forma modulare. Quando Γ e k sono tali che lo spazio delle forme cuspidali è zero, si ottengono risultati esatti.
Quando si considerano funzioni della teoria dei numeri ϕ, per esempio quando ϕ(n) è la funzione numero delle rappresentazioni per una forma quadratica con un numero dispari di variabili, si è condotti a forme modulari il cui peso k non è la metà di un intero. Questo fa sorgere un'ambiguità in (cz + d)2k che deve essere chiarita separatamente per ciascuna
in Γ. Questa ambiguità può non essere risolubile in un modo sufficientemente coerente da permettere l'esistenza di funzioni che soddisfino l'identità
Bisogna allora accontentarsi di funzioni f che soddisfano la
ove vk è una funzione da Γ ai numeri complessi di modulo 1, che viene chiamata ‛sistema di moltiplicatori'. Una volta introdotti i sistemi di moltiplicatori, si possono esaminare forme automorfe di dimensione reale arbitraria. In un lungo lavoro pubblicato nel 1930, Petersson, un allievo di Hecke, affrontò sistematicamente questa questione.
Un sistema di moltiplicatori può essere considerato come una rappresentazione proiettiva di dimensione 1 di Γ per la restrizione a Γ di un moltiplicatore proiettivo σK per SL(2, R), il quale è banale, ma non identicamente uguale a 1, su Γ. Uno dei risultati di Petersson fu la dimostrazione che, per ogni numero reale k, il σk corrispondente è di fatto banale sul gruppo modulare, così che esistono opportune vk. In questo e in lavori successivi, Petersson generalizzò la teoria di Hecke delle forme cuspidali e delle serie di Eisenstein a gruppi fuchsiani più generali e a forme di peso positivo generico.
Tenendo presente l'esempio delle funzioni abeliane come caso particolare importante, è naturale cercare di generalizzare la teoria delle funzioni e delle forme automorfe a una corrispondente teoria per funzioni di più variabili complesse. Tuttavia, prima di tentare di descrivere che cosa è stato fatto in questo senso, sarà opportuno esaminare un aspetto diverso nel quale la teoria dei gruppi è legata alla teoria delle funzioni di una variabile complessa. Consideriamo la serie di Fourier
e ricordiamo che n ???14??? einϑ è il più generale carattere unitario a una dimensione del gruppo additivo Z di tutti gli interi n. Se si omette la condizione di unitarietà, il carattere più generale è n ???14??? rneinϑ , ove r è un arbitrario numero reale positivo, cosicché è naturale estendere la funzione periodica a una funzione
definita sul gruppo di ‛tutti' i caratteri di Z, unitari o no. Se questa serie converge, essa convergerà per tutti gli r, ϑ, con r in un intervallo finito o infinito, e definirà ivi una funzione che è una funzione analitica della variabile complessa z = reiϑ. Di fatto, come funzione di z, la serie non è altro che la serie di potenze doppiamente infinita (serie di Laurent)
Inversamente, se
converge per r1 〈 ∣ z ∣ 〈 r2 e r1 〈 1 〈 r2, la funzione
può ottenersi dalla serie di Fourier
nel modo che abbiamo or ora descritto. Similmente, il carattere più generale del gruppo additivo della retta reale è
t ???14??? ei(x+iy)t = eixte-yt = eizt
e la trasformata di Fourier
può essere estesa alla formula
la quale converge quando y sta in un intervallo ed è analitica nella striscia corrispondente nel piano delle z. Quando f è zero per t negativo ed è sommabile, la corrispondente funzione di z è definita e analitica nel semipiano superiore ed è essenzialmente la cosiddetta ‛trasformata di Laplace' di f. Più in generale, sia G un arbitrario gruppo commutativo localmente compatto e separabile sia Ø il suo gruppo dei caratteri e sia À lo spazio vettoriale degli omomorfismi continui di G nel gruppo additivo della retta reale. L'omomorfismo continuo più generale di G nel gruppo moltiplicativo dei numeri complessi non nulli è x ???14??? χ(x)el(x), ove χ ∈ Ø, l ∈ À e la trasformata di Fourier generalizzata può essere estesa a una trasformata di Laplace generalizzata (bilaterale) f???43???(χ, l) = ∫ f(x)χ(x)el(x) definita su (una parte) di Ø × À. Se Ø è connesso e À è di dimensione finita, su Ø × À opera ergodicamente À ⊕ À e sulle orbite si ha una struttura complessa definita a partire da quella ovvia in À ⊕ À. Si dice che una funzione su Ø × G è ‛analitica' se essa è una funzione di Borel su Ø × À ed è analitica sulle orbite. In questo senso le trasformate di Laplace sono analitiche nell'interno dei loro domini di definizione. Si ha una dualità fra certi coni convessi in À e certi sottosemigruppi di G, tale che, quando G0 ⊆ G corrisponde a C ⊆ À, C è l'insieme di tutti gli l in À tali che l(x) ≤ 0 per tutti gli x in G0 e viceversa. Il considerare le funzioni analitiche come famiglie di trasformate di Fourier parametrizzate da caratteri reali non unitari fornisce alcune utili informazioni e, in una certa misura, permette di dedurre dei teoremi relativi alle funzioni analitiche da teoremi dell'analisi armonica. D'altra parte, il passaggio da Ø a Ø × À fornisce all'analisi armonica una maggiore flessibilità e profondità, simile a quella che si ottiene passando al piano complesso nella teoria degli integrali algebrici. Si veda, per esempio, il libro di Paley e Wiener, Fourier trasforms in the complex domain, pubblicato nel 1934, e l'articolo monografico di Zygmund, Complex methods in the theory of Fourier series, del 1943. Come abbiamo già indicato nel cap. 13, una serie di Dirichlet
Σ ane-λn(σ+iτ)
può essere considerata come un'estensione al piano complesso della funzione quasi periodica
τ ???14??? Σ ane-λnσe-iλnτ.
Mentre ogni superficie di Riemann si può ottenere come spazio delle orbite di un gruppo discreto Γ di G su uno spazio quoziente G/K, ove G è un gruppo di Lie connesso, questo purtroppo non accade per varietà complesse di dimensione superiore. In particolare, una varietà complessa semplicemente connessa non ammette necessariamente un gruppo transitivo di isomorfismi in se stessa. Ne segue che la teoria generale delle varietà complesse è legata assai meno strettamente alla teoria dei gruppi di quanto non lo sia la teoria delle superfici di Riemann. D'altra parte, quelle varietà complesse che possono essere ottenute come spazi di Γ-orbite di spazi quozienti G/K formano una famiglia importante e interessante, il cui studio è legato alla teoria dei gruppi nella stessa misura in cui lo è lo studio delle superfici di Riemann. Ci si può fare un'idea della vastità di questa famiglia considerando i fatti seguenti. Nel 1935 H. Cartan dimostrò che il gruppo G di tutti gli automorfismi (isomorfismi su se stesso) di un sottoinsieme aperto connesso limitato dello spazio delle n-uple di numeri complessi è un gruppo di Lie e che il sottogruppo che lascia un punto fisso è compatto. Pertanto, ogniqualvolta il gruppo è transitivo, la varietà complessa corrispondente sarà uno spazio quoziente G/K con G gruppo di Lie e K sottogruppo compatto. Nello stesso anno É. Cartan pubblicò un importante lavoro in cui dimostrò che l'azione in questione è transitiva se l'insieme aperto limitato e connesso è ‛simmetrico', nel senso che ogni punto è punto fisso isolato di un automorfismo di periodo 2. Egli mostrò inoltre che il gruppo degli automorfismi nel caso simmetrico è un gruppo di Lie semisemplice privo di componenti compatti. Applicando la classificazione dei gruppi di Lie semisemplici, egli riuscì a dare una classificazione completa di tutti i ‛domini limitati simmetrici'. Ogni dominio siffatto è un prodotto di domini che sono ‛irriducibili', nel senso che essi non sono prodotti di domini simmetrici di dimensione più bassa, e i domini irriducibili corrispondono biunivocamente a certi gruppi di Lie semplici non compatti con centro banale. Tutti questi gruppi di Lie, a eccezione di due, appartengono a quattro famiglie infinite di gruppi di Lie semplici reali e, corrispondentemente, si hanno domini di Cartan di tipo I, II, III e IV. Cartan dimostrò inoltre che la transitività implica la simmetria purché la dimensione (complessa) non superi 3. Se questo fatto fosse ancora valido in dimensioni superiori rimase insoluto fino a che, nel 1959, Pjatetskij-Shapiro costruì controesempi in dimensioni 4 e 5. Pjatetskij-Shapiro fornì inoltre un'analisi dettagliata di tutti i domini limitati omogenei (insiemi aperti connessi e limitati sui quali G opera transitivamente). Questo lavoro, pubblicato all'inizio del 1960, fu compiuto in parte in collaborazione con Vinberg e Gindikin. In esso venivano applicati risultati antecedenti di Borel e di Koszul. Nell'ambito di una problematica diversa, H. C. Wang, nel 1954, classificò tutte le varietà complesse compatte omogenee e semplicemente connesse. Nel 1947 Bochner e Montgomery mostrarono che il gruppo degli automorfismi di una varietà siffatta (fosse essa semplicemente connessa oppure no) è un gruppo di Lie complesso. Wang mostrò che un sottogruppo compatto semisemplice opera transitivamente, cosicché il problema si riduce a studiare certi spazi quozienti di gruppi di Lie compatti e semisemplici.
Si può pensare alle varietà complesse compatte omogenee semplicemente connesse come ad analoghi del piano complesso ⋃∞ e ai domini limitati simmetrici (o più in generale ai domini limitati omogenei) come oggetti analoghi al semipiano superiore o, equivalentemente, alla parte interna del disco unità. L'equivalenza fra il semipiano superiore e la parte interna del cerchio unità ha un analogo nel fatto che un dominio limitato simmetrico può essere realizzato come spazio quoziente G/K, dove K è compatto.
Le ricerche sulle funzioni e sulle forme automorfe per varietà complesse omogenee di dimensione maggiore di 1 ebbero inizio subito dopo il lavoro originale di Poincaré a opera di Ch.-É. Picard e G. Fubini e vennero continuate nel primo quarto del XX secolo da G. Gerard, P. J. Myrberg e da altri. Tuttavia la teoria moderna affonda le sue radici nell'opera di C. L. Siegel sulle forme quadratiche, apparsa verso la fine del 1930. Abbiamo già osservato, nel cap. 13, come Siegel mostrò che il suo risultato centrale era equivalente a una certa identità tra forme automorfe in più variabili complesse. Le varietà complesse che vi appaiono sono elementi di quella classe di domini di Cartan per i quali il gruppo degli automorfismi è Sp(n, R), cosicché la varietà è Sp(n, R)/SU(n). Ora, Sp(1, R) è isomorfo a SL(2, R) e Sp(1, R)/SU(1) è il semipiano superiore. Così Sp(n, R)/SU(n) è una generalizzazione diretta del semipiano superiore, che si chiama oggi ‛semipiano superiore di Siegel'. Esso può essere realizzato concretamente come spazio delle matrici X + iY dove X e Y sono matrici reali simmetriche n × n e Y è definita positiva. Il ‛gruppo modulare' di tutte le matrici intere in Sp(n, R), quando opera sullo spazio di tutte le X + iY, contiene in particolare le trasformazioni X + iY ???14??? X + A + iY, ove A è una matrice simmetrica a elementi interi. Inoltre una ‛forma modulare' è necessariamente invariante rispetto a queste trasformazioni. Pertanto una forma modulare determina, e ne è determinata, una funzione a valori complessi sullo spazio vettoriale di tutte le X, la quale è costante sulle classi laterali di un sottogruppo discreto a quoziente compatto, e quindi è determinata da una serie di Fourier multipla. Come nel caso classico, i coefficienti di Fourier hanno significato nella teoria dei numeri. Le ricerche volte a estendere i risultati di Poincarè ed Hecke a questi ‛semipiani superiori' di dimensione maggiore di 1 e a forme automorfe relative a opportuni sottogruppi discreti di Sp(n, R) vennero iniziate da Siegel e dalla sua allieva H. Braun verso la fine del 1930, sviluppate ulteriormente da Siegel e da L. K. Hua agli inizi del 1940 e continuate negli anni successivi dallo stesso Siegel, da H. Maass e da altri. Anche altri domini di Cartan vennero considerati, sia pure in minor dettaglio. Fra le esposizioni generali importanti di questa teoria vanno ricordate le lezioni tenute da Siegel a Princeton nel 1950, Analitic functions of several complex variables, e il libro di Pjatetskij-Shapiro, Geometry of classical domains and theory of automorphic functions, pubblicato in russo nel 1961 e tradotto in francese e in inglese rispettivamente nel 1966 e nel 1969. Il semipiano superiore di Siegel, espresso in forma matriciale, come abbiamo detto dianzi, può anch'esso essere considerato un dominio per trasformazioni di Laplace generalizzate. Si considera l'insieme di tutte le matrici X come il duale di un gruppo vettoriale reale G di dimensione finita e quindi l'insieme di tutte le Y è un cono aperto in À. Mantenendo G invariato, ma prendendo un cono Y più generale, M. Koecher, nel 1954, sviluppò una corrispondente generalizzazione dei semipiani superiori di Siegel. Varietà complesse generali di questo tipo si presentano anche nelle ricerche di Pjatetskij-Shapiro e dei suoi collaboratori. In tali lavori esse vengono chiamate domini di Siegel di prima specie. Alcune di esse sono isomorfe a domini limitati omogenei non simmetrici.
Nel 1949 H. Maass diede inizio a un nuovo sviluppo di considerevole importanza. La teoria di Hecke descritta nel cap. 13, che permette di applicare la teoria delle forme modulari alla ricerca delle serie di Dirichlet che soddisfano un'equazione funzionale, è efficace soltanto per una classe fortemente limitata di equazioni funzionali. In particolare, essa non è efficace per l'equazione funzionale soddisfatta dalla funzione zeta di una estensione quadratica reale dei razionali. Maass scoprì che si può ampliare la teoria, in modo da includere questo caso al pari di altri, introducendo forme automorfe che non sono funzioni analitiche complesse, ma sono invece autofunzioni dell'operatore differenziale
Maass scoprì che era possibile estendere molti aspetti della teoria di Hecke alle sue ‛forme automorfe non analitiche' e in particolare era possibile scrivere queste ultime come somme di ‛forme cuspidali' e ‛serie di Eisenstein'. La serie di Eisenstein formale
ove la somma è estesa a certe coppie di interi m, n, converge quando la parte reale di s è più grande di 1 e soddisfa l'equazione differenziale
Tuttavia, perchè s(s − 1) sia reale e maggiore di 1/4, s deve avere parte reale uguale a 1/2. Maass superò questa difficoltà mostrando che E(s, z), come funzione di s, può essere prolungata in modo da essere meromorfa per tutti gli s e da soddisfare un'equazione funzionale che lega i suoi valori in s a quelli in 1 − s. In particolare essa è ben definita quando s ha parte reale uguale a 1/2. In lavori successivi Maass estese la sua teoria al semipiano superiore di Siegel e anche in altre direzioni. Tuttavia a questo punto il passo decisivo fu compiuto da A. Selberg nel suo famoso articolo del 1956, al quale abbiamo già accennato nei capp. 13 e 14. Selberg sostituì la varietà complessa omogenea di Maass con un più generale spazio riemanniano ‛debolmente simmetrico' non necessariamente dotato di una struttura complessa. Questo concetto include quello di spazio quoziente più generale G/K, ove G è un gruppo di Lie semisemplice connesso con un centro finito e privo di componenti compatte e K è un sottogruppo compatto massimale. Discuteremo qui soltanto questo caso. L'operatore differenziale
viene sostituito da una famiglia finita, D1, ..., Dn, di operatori differenziali su G/K = S, che sono invarianti rispetto all'azione di G e generano l'anello di tutti gli operatori differenziali invarianti. Sia Γ un sottogruppo discreto di G e sia L una rappresentazione unitaria di dimensione finita di Γ (non esclusa la rappresentazione identica a una dimensione). Consideriamo le funzioni differenziabili F da S allo spazio vettoriale ℋ(L) che: a) sono autofunzioni di D1, ..., Dn simultaneamente; b) hanno la proprietà di invarianza F(sx) = Lx(F(s)) per ogni s in S e ogni x in G. Un lemma importante (strettamente connesso all'osservazione di I. M. Gelfand, secondo la quale UIK ha un'algebra commutante commutativa; v. sopra, cap. 14) afferma che gli operatori Dj commutano. Le funzioni F soddisfacenti la b) hanno la proprietà che la funzione s ???14??? F(s)•F(s) è Γ invariante e può essere integrata sopra un dominio fondamentale facendo diventare l'insieme delle F per le quali l'integrale è finito uno spazio di Hilbert ℋΓ. Quando G/Γ è compatto, si ha una base ortonormale per ℋΓ, che è costituita dalle funzioni F che soddisfano a) e b). Ora, ogni funzione k su G, soddisfacente opportune condizioni, che sia costante sulle classi laterali doppie di K : K, definisce un operatore integrale in ℋΓ che è diagonalizzato dalla base or ora descritta. Il risultato principale di Selberg, la sua ‛formula della traccia', è una relazione che esprime la somma degli elementi diagonali in funzione dei valori presi da k sugli elementi di G che sono coniugati di elementi di Γ. Come abbiamo osservato dianzi, essa può essere considerata come una generalizzazione della formula sommatoria di Poisson e, al pari di quest'ultima, ha importanti conseguenze nell'ambito della teoria dei numeri. Selberg considerò anche il problema di generalizzare la sua formula della traccia al caso in cui G/Γ non è compatto ma ha una misura invariante finita. Qui gli operatori in ℋΓ definiti da k e gli operatori Dj possono avere spettri continui e l'operatore definito da k deve ammettere un operatore, avente lo stesso spettro continuo, sottraendo il quale ciò che resta ha soltanto uno spettro discreto. Nella formula della traccia che ne risulta intervengono valori di k su elementi di G non coniugati a elementi di Γ. La situazione è piuttosto complicata e i risultati di Selberg si sono rivelati assai meno completi che nel caso in cui lo spettro è discreto. Grosso modo, ogni punto nella compattificazione dello spazio delle orbite di Γ operante su G/K porta un contributo allo spettro continuo. Selberg si è occupato dettagliatamente soltanto del caso classico in cui G = SL(2, R) e Γ ammette una compattificazione con l'aggiunta di un solo punto. L'operatore integrale modificato viene costruito partendo da forme automorfe del tipo di Maass associate allo spettro continuo di
Come nelle ricerche di Maass, queste sono ottenute come prolungamenti analitici delle serie di Eisenstein.
Una visione assai più approfondita delle ricerche di Maass e di Selberg si ottiene tenendo conto della stretta relazione esistente tra le rappresentazioni del gruppo unitario e le forme automorfe, relazione segnalata da Gelfand e Fomin per la prima volta nel 1952 ed esplorata in modo più generale e sistematico da Gelfand e Pjatetskij-Shapiro nel 1959. Per ogni intero positivo k e ogni x =
in SL(2, R), sia Wkx l'operatore lineare che trasforma una funzione olomorfa a valori complessi f, definita sul semipiano superiore, nella funzione
Si verifica immediatamente che x ???14??? Wkx è una rappresentazione di SL(2, R) e che le forme automorfe olomorfe di peso k per un sottogruppo discreto Γ sono esattamente le funzioni f lasciate invariate da tutte le Wkγ con γ in Γ. Quelle funzioni olomorfe f per le quali
∫ ∫ ∣ f(x + iy) ∣2 y2k-2 dxdy 〈 ∞
costituiscono uno spazio di Hilbert ℋk che è Wkx invariante e sul quale le Wkx sono unitarie. Queste rappresentazioni unitarie di SL(2, R) sono irriducibili e costituiscono una metà della ‛serie discreta' di questo gruppo (v. sopra, cap. 8). Nel caso particolare in cui G/Γ è compatto, Gelfand e Fomin mostrarono che la rappresentazione unitaria di G definita dall'azione naturale di G su ℒ2(G/Γ) è una somma diretta discreta di rappresentazioni irriducibili e il numero di volte che una Wk appare in tale somma è la dimensione dello spazio delle forme automorfe di peso k per Γ. Pertanto il problema dell'esistenza per le forme automorfe è strettamente connesso alla struttura della rappresentazione indotta UIK. Naturalmente la ricerca della molteplicità delle Wk costituisce soltanto una parte del problema di trovare la struttura di UIK. In particolare, per ogni numero reale r, l'applicazione
è una rappresentazione unitaria di dimensione 1, χr, del sottogruppo indicato e, quando r ≠ 0, la rappresentazione indotta Uχr è irriducibile e ci si può chiedere quale sia la molteplicità di Uχr. Gelfand e Pjatetskij-Shapiro hanno dimostrato che questa molteplicità è uguale alla dimensione dello spazio di tutte le soluzioni Γ invarianti dell'equazione differenziale
e pertanto è uguale alla dimensione di uno spazio di forme automorfe non analitiche nel senso di Maass. Poiché le serie discrete e le Uχr costituiscono quasi tutte le classi di equivalenza di rappresentazioni unitarie irriducibili di SL(2, R), si vede che le forme automorfe di Maass costituiscono un complemento del tutto naturale alle forme automorfe analitiche classiche. Partendo da questo punto di vista, Selberg ha affrontato lo studio della struttura di UIΓ e, più in generale, di UL, dove L è una rappresentazione unitaria arbitraria di dimensione finita di un opportuno sottogruppo discreto Γ di un gruppo di Lie G semisemplice connesso arbitrario con centro finito e privo di componenti compatte. Se K è un sottogruppo compatto massimale di G, le componenti (infinitesime) irriducibili della rappresentazione indotta UIK sono autospazi (infinitesimi) degli operatori differenziali invarianti di G/K e gli autovalori corrispondenti possono essere usati per parametrizzare queste componenti irriducibili. Quando G/Γ è compatto, la formula della traccia di Selberg (come già abbiamo osservato nel cap. 14) risulta coincidere essenzialmente con la formula di Plancherel per la rappresentazione indotta UL. Quando G/Γ non è compatto, UL, in generale, non potrà essere decomposta in modo discreto e il problema di esaminare la parte continua è estremamente complesso. Naturalmente esso è l'equivalente, nell'ambito delle rappresentazioni, del problema che nasce dagli spettri continui degli operatori differenziali di Selberg. A esso può essere applicato il metodo di Maass e Selberg del prolungamento analitico delle serie di Eisenstein. Con un'enunciazione leggermente diversa, il problema dell'estensione della formula della traccia di Selberg al caso in cui G/Γ non è compatto si riduce essenzialmente al problema di studiare la struttura della parte della rappresentazione indotta UL che non può essere decomposta in modo discreto. Questo studio può essere sviluppato facendo ricorso alla teoria dei prolungamenti analitici delle serie di Eisenstein. Contributi alla sua soluzione sono stati apportati da Gelfand e Selberg, ma i risultati più completi e più generali sono dovuti a R. P. Langlands che, sotto ipotesi molto generali, mostrò che appropriate serie di Eisenstein possono essere prolungate analiticamente in modo da soddisfare opportune equazioni funzionali. Un resoconto dettagliato di gran parte delle ricerche di Langlands si trova in note di seminario di Harish-Chandra pubblicate nel 1968.
Quella parte delle ricerche di Maass (e di Hecke) che si riferisce ai rapporti fra le forme modulari e le serie di Dirichlet con i prodotti di Eulero viene meglio compresa quando s'introducano opportuni gruppi adelici. Sia GA il gruppo adelico di SL(2, Q), cosicché GA è un sottogruppo di SL(2, R) × Πp SL(2, Qp) dove Q è il corpo dei numeri razionali e Qp è il corpo dei numeri p-adici. Sia Γ il sottogruppo delle adeli principali; Γ è un sottogruppo chiuso di GA, canonicamente isomorfo a SL(2, Q). Sia Γ0 = Γ ⋂ [SL(2, R) × Πp SL(2, p), ove Zp è l'anello degli interi p-adici. Osserviamo che l'isomorfismo canonico di Γ con SL(2, Q) applica Γ0 su SL(2, Z) e identifica Γ0 con il sottogruppo discreto SL(2, Z) di SL(2, R). D'altra parte SL(2, Z) ha un'immersione canonica densa in Πp SL(2, Zp). Sia ???45???-o l'insieme di tutte le classi di equivalenza delle rappresentazioni unitarie irriducibili di SL(2, Z) che si estendono a rappresentazioni unitarie della compattificazione Πp SL(2, Zp). Una semplice argomentazione, basata su teoremi generali, relativi alle rappresentazioni indotte, mostra che la restrizione a SL(2, R) × Πp SL(2, Zp) della rappresentazione UIΓ di GA, indotta dalla rappresentazione identica IΓ di Γ, è equivalente alla
ove Ë′ è l'aggiunta dell'estensione, univocamente definita, L′ di L a Πp SL(2, Zp). Pertanto la restrizione di UIΓ a SL(2, R) × e, e, ... è equivalente a
Dall'identificazione di Γ0 con la sua immagine SL(2, Z) in SL(2, R) segue che la rappresentazione indotta UIΓ0 di SL(2, R) è canonicamente equivalente a una sottorappresentazione di UIΓ ristretta a SL(2, R) × e, e, ...
Spostando l'attenzione da UIΓ0 alla rappresentazione UIΓ di GA, si studiano di fatto simultaneamente tutte le rappresentazioni indotte UL di SL(2, R). La rappresentazione indotta UL svolge naturalmente, per le forme modulari a valori vettoriali e soddisfacenti la
lo stesso ruolo che UIΓ svolge per quelle più usuali. Inoltre, se Γ00 è un sottogruppo di congruenza principale di Γ0 di indice finito, UIΓ00 è una somma finita di rappresentazioni di tipo UL, ove L è in ???45???-o. Questa equivalenza fra rappresentazioni stabilisce una corrispondenza lineare tra spazi di funzioni su SL(2, R) e spazi di funzioni sul gruppo adelico GA. In particolare, forme modulari sul semipiano superiore possono essere identificate con funzioni su SL(2, R) e quindi con funzioni su GA; si può pertanto parlare di forme modulari su un gruppo adelico. Se una particolare rappresentazione unitaria irriducibile π di SL(2, R) appare con molteplicità finita j nella decomposizione di UIΓ0, si vede facilmente che esistono j sottorappresentazioni irriducibili non equivalenti N1, N2, ..., Nj di Πp SL(2, Qp) tali che π × Nj è una componente irriducibile di UIΓ. La restrizione di ciascuna di queste a SL(2, R) contiene π con molteplicità uno e definisce, pertanto una decomposizione canonica della π componente di UIΓ0 come somma diretta di j rappresentazioni irriducibili equivalenti. Corrispondentemente, lo spazio a j dimensioni delle forme modulari corrispondenti a π ha una decomposizione canonica come somma diretta di sottospazi a una dimensione. Gli elementi di questi sottospazi a una dimensione sono esattamente le forme modulari, le cui serie di Dirichlet associate hanno prodotti di Eulero nella teoria di Hecke; essi sono, cioè, le autofunzioni dei cosiddetti ‛operatori di Hecke'. Inoltre, se f è una forma modulare nel sottospazio a una dimensione associato a Ni, il fattore del corrispondente prodotto di Eulero associato al numero primo p può essere calcolato in modo semplice, non appena sia nota la SL(2, Qp) componente di Ni. In breve, tutta la teoria di Hecke è essenzialmente contenuta nelle proprietà della rappresentazione UIΓ di GA e della sua restrizione a SL(2, R) e SL(2, Qp). Le considerazioni precedenti suggeriscono ampie generalizzazioni dei risultati di Hecke e Maass. Esse sono state di fatto sviluppate molto dettagliatamente in una lunga memoria recente di Langlands e Jacquet per il caso particolare in cui, in luogo di SL(2, Q), si consideri SL(2, k) ove k è un'arbitraria estensione finita di Q. Di fatto i due autori lavorano su GL(2, k) invece che su SL(2, k) e sostituiscono le rappresentazioni unitarie con una certa classe di rappresentazioni su uno spazio vettoriale astratto. Una parte considerevole delle loro ricerche consiste nello studio delle rappresentazioni irriducibili dei gruppi totalmente sconnessi GL(2, kp), assegnando a essi ‛fattori di Eulero' che soddisfano ‛equazioni funzionali locali'. L'opera di Jacquet e Langlands si ispira direttamente a un lavoro di A. Weil del 1967, nel quale vengono stabilite certe generalizzazioni intermedie dei risultati di Hecke. Weil ha affrontato il caso più generale seguendo un'altra via, nella quale compaiono le adeli, ma le rappresentazioni dei gruppi non vengono messe in rilievo. Gran parte dell'interesse suscitato da questi risultati sta nella loro possibile utilizzazione per generalizzare la legge di reciprocità di Artin (v. sopra, cap. 13) dimostrando che varie serie di Dirichlet, definite nell'ambito della teoria dei numeri coincidono di fatto con serie di Dirichlet associate con forme modulari generalizzate. Come abbiamo spiegato nel cap. 13, queste identificazioni hanno conseguenze di notevole interesse nell'ambito della teoria dei numeri. Langlands s'interessa particolarmente a questo problema per certe generalizzazioni delle L-funzioni di Artin introdotte da Weil. Il gruppo di Weil WK/F di un'estensione di Galois K di un corpo di numeri algebrici F contiene il gruppo delle classi di idèle di K come sottogruppo normale e il gruppo di Galois G(K/F) è il corrispondente quoziente. Le L-funzioni di Weil sono parametrizzate da rappresentazioni di dimensione finita di WK/F e Langlands spera di associare una rappresentazione irriducibile π(σ) del gruppo adelico di GL(n, F) a ogni rappresentazione σ a n dimensioni di WK/F e quindi di identificare la L-funzione di Weil di σ con una serie di Dirichlet legata a π(σ) nel modo suggerito dalle precedenti considerazioni su SL(2, Q). Uno dei risultati principali del lavoro di Jacquet-Langlands afferma che questa identificazione può di fatto attuarsi per certe rappresentazioni σ a due dimensioni. Per trattare rappresentazioni di dimensione più elevata di σ bisogna estendere la teoria di Hecke a gruppi algebrici più generali - specialmente al gruppo GL(n, F) ove F è preso come dianzi. Corrispondentemente, ciò richiede una conoscenza dettagliata della teoria delle rappresentazioni degli analoghi p-adici dei gruppi di Lie semisemplici, conoscenza che per ora si ha soltanto per GL(2, F).
Le applicazioni delle forme automorfe alla teoria delle forme quadratiche, sviluppata da Hecke e da Siegel e generalizzata più tardi con risultati relativi ai numeri di Tamagawa di gruppi algebrici semisemplici (v. sopra, cap. 13), possono essere considerate anche dal punto di vista delle rappresentazioni dei gruppi. In due lunghi articoli pubblicati negli ‟Acta mathematica" del 1964 e 1965, Weil ha dimostrato un teorema generale sulle funzioni su certi gruppi adelici che contiene come corollari molti dei risultati noti sui numeri di Tamagawa di gruppi algebrici semisemplici. I risultati più importanti del primo lavoro si riferiscono a teoremi sulle rappresentazioni unitarie di gruppi simplettici generalizzati e comprendono una trattazione delle funzioni theta dal punto di vista della teoria delle rappresentazioni.
Generalizzata nella direzione suggerita dall'opera di Selberg, la teoria delle forme automorfe diventa più o meno equivalente alla teoria delle rappresentazioni indotte del tipo UL, ove L è una rappresentazione unitaria di dimensione finita di un opportuno sottogruppo chiuso numerabile Γ di un gruppo di Lie semisemplice G di tipo generale, con centro finito e privo di componenti compatte. L'interesse si rivolge quindi in modo particolare allo studio dei possibili Γ per siffatti gruppi di Lie G semisemplici e alle proprietà geometriche degli spazi omogenei G/Γ, in vista di una generalizzazione di ciò che è stato fatto da Poincaré per SL(2, R). Una classe importante di gruppi Γ è quella dei cosiddetti ‛sottogruppi aritmetici'. Si realizza G come gruppo di punti, reali di un gruppo algebrico di matrici definito su Q e, per ogni realizzazione siffatta, il sottogruppo delle matrici intere a determinante ± 1 è un sottogruppo aritmetico. La ricerca dei domini fondamentali per gruppi aritmetici si particolarizza, quando G = GL(n, R), al problema classico della riduzione per forme quadratiche definite positive. La soluzione data da Hermite a quest'ultimo problema si generalizza, come hanno dimostrato Borel e Harish-Chandra nel 1962. Sebbene i sottogruppi discreti di SL(2, R) costituiscano un'eccezione e sebbene A. A. Markov jr. e Vinberg abbiano recentemente mostrato con esempi che ve ne sono altri, esistono tuttavia buone ragioni per ritenere che una gran parte dei sottogruppi discreti dotati di proprietà ‛ragionevoli' siano di fatto aritmetici.
Traendo ispirazione dal lavoro originale di Poincaré sulle forme automorfe e sul gruppo fondamentale, una notevole quantità di lavori si è sviluppata intorno allo studio dei gruppi astratti numerabili e in particolare alla definizione di questi gruppi mediante ‛generatori e relazioni'. Diremo che gli elementi x1, x2, ... ‛generano' Γ se Γ è il solo sottogruppo che li contiene tutti. Si dice che il gruppo è ‛libero' se i generatori possono essere scelti in modo tale che, ogniqualvolta y1, y2, ..., yn è un insieme finito di elementi distinti costituito da generatori e dai loro inversi e inoltre yjyj+1 ≠ e per ogni j, allora y1y2...yn ≠ e. Un gruppo libero è chiaramente determinato a meno di isomorfismi dal numero cardinale del suo insieme di generatori e ogni gruppo numerabile è canonicamente un'immagine omomorfa di un gruppo libero avente gli stessi generatori. Gli elementi del gruppo libero che stanno nel nucleo di questo omomorfismo si dicono ‛relazioni' e il gruppo viene definito indicando un gruppo di generatori in modo tale che il sottogruppo ‛normale' più piccolo che li contiene tutti è esattamente il gruppo delle relazioni. Quando le relazioni sono in numero finito, il gruppo si dice ‛a presentazione finita'. Quando Γ è un sottogruppo chiuso di SL(2, R), tale che SL(2, R)/Γ è compatto, segue dalle ricerche di Poincaré che Γ ha 2g generatori A1, B1, ..., Ag, Bg ed è definito da questi generatori e dalla semplice relazione
A1B1A1-1B1-1...AgBgAg-1Bg-1 = e,
ove g è il genere della superficie di Riemann definita da Γ. Borel e Harish-Chandra, nel lavoro citato più sopra, mostrarono che ogni gruppo aritmetico Γ ha generazione finita. H. Behr mostrò poi che ogni Γ siffatto ha anche presentazione finita e ha soltanto un numero finito di classi di coniugio di sottogruppi finiti. Dato Γ come gruppo astratto, ci si può chiedere quali siano i diversi modi di immergerlo in G. È noto da molto tempo ormai che, quando G = SL(2, R) e G/Γ è compatto, esiste un continuo pluridimensionale di sottogruppi Γ′ che non sono mutuamente coniugati, sono isomorfi a Γ e tali che G/Γ′ è compatto. Questa situazione è in netto contrasto con quella che si presenta per moltissimi gruppi di Lie semisemplici, per i quali i sottogruppi Γ chiusi e numerabili, tali che G/Γ è compatto, sono ‛rigidi' nel senso che un Γ′ isomorfo a Γ (e con G/Γ′ compatto) è coniugato a Γ purché sia abbastanza vicino a Γ in una certa ovvia topologia. Questi fatti furono scoperti da Calabi e Vesentini, Selberg e Weil all'inizio degli anni sessanta. Strettamente connesso a questi risultati è il recente teorema di rigidità di Mostow, secondo il quale ogni isomorfismo di Γ su Γ′ può essere esteso a un isomorfismo di gruppi di Lie di G su G′ quando G/L e G′/L′ sono compatti e G e G′ sono gruppi di Lie semisemplici semplicemente connessi soddisfacenti alcune altre deboli condizioni. Si confrontino in proposito i risultati sulle nilvarietà e sulle varietà risolubili citati nel cap. 12.
Come abbiamo indicato precedentemente, le ‛cuspidi' per un dominio fondamentale di un sottogruppo numerabile chiuso Γ di SL(2, R), operante sul semipiano superiore, cornspondono biunivocamente in modo naturale a certe classi laterali doppie di T : Γ, ove T è il sottogruppo di tutte le matrici
in SL(2, R) con c = 0. Un risultato corrispondente vale quando Γ è un sottogruppo aritmetico di un gruppo di Lie G semisemplice opportunamente ristretto, ma ora T deve essere sostituito da un insieme finito di gruppi e precisamente da un insieme di rappresentanti P1, P2, ..., Pk delle classi di coniugio dei sottogruppi parabolici di G (v. sopra, cap. 9). Se Uj, è il radicale unipotente di Pj, Pj × Γ corrisponde a una ‛cuspide' se, e soltanto se, xΓx-1 ⋂ Uj ha uno spazio compatto di classi laterali destre in Uj Utilizzando tale compattezza, si può dimostrare che l'operatore di intrecciamento formale della classe laterale doppia (v. sopra, cap. 12) associato a Uj × Γ definisce di fatto un operatore d'intrecciamento che stabilisce un'equivalenza fra la rappresentazione indotta UIPj e una sottorappresentazione di UIΓ. Questa sottorappresentazione dipende soltanto dalla cuspide Pj × Γ. La sottorappresentazione massimale di UIΓ, che è ortogonale alla sottorappresentazione definita dalle cuspidi, è (come Gelfand e Pjatetskij-Shapiro hanno dimostrato nel 1963) una somma diretta discreta di rappresentazioni irriducibili. Pertanto il metodo orosferico di Gelfand (v. sopra, cap. 14) può essere utilizzato per ridurre la ricerca della ‛parte continua' di UIΓ al problema più facile) di trovare la struttura delle UIPj ogni cuspide porta un contributo. La relazione tra le classi laterali doppie Pj × Γ e la geometria delle Γ-orbite in G/K può essere chiarita mediante la nozione di ‛frontiera' per spazi omogenei introdotta da Furstemberg nel 1963. Sia μ una misura in uno spazio quoziente compatto G/T, tale che μ(G/T) = 1, e sia H il sottogruppo chiuso degli x in G che traslano μ in se stessa. Lo spazio quoziente G/H può essere identificato con l'insieme di tutte le misure su G/T ottenute traslando μ. Supponiamo che una successione μ1, μ2, ... di tali traslate converga al punto m0 in G/T, nel senso che
∫ f(m) dμj(m)
converga a f(m0) per ogni funzione continua f su G/T. Le traslate delle μj mediante y convergeranno a m0y per ogni y e ogni punto di G/T può essere considerato come un limite della successione di punti di G/H. In questo senso, lo spazio quoziente G/T è parte della ‛frontiera' di G/H. Quando T = Pj, c'è una sola scelta per μ per la quale K ⊆ H. A parte alcune eccezioni, si ha K = H, cosicché G/Pj può essere considerato come una parte della ‛frontiera' di G/K. Corrispondentemente, le classi laterali doppie di Pj : Γ possono essere considerate come punti nella ‛frontiera' dell'insieme di tutte le classi laterali doppie di K : Γ, cioè l'insieme delle Γ-orbite in G/K. Le idee di Furstemberg vennero ulteriormente analizzate e sviluppate da C. C. Moore nel 1964. Fra l'altro Moore mostrò che le ‛compattificazioni' di G/K ottenute aggiungendo le frontiere G/Pj sono identiche a certe compattificazioni introdotte anni prima da Satake.
Dalla connessione fra forme automorfe generali e rappresentazioni unitarie di gruppi adelici nasce il problema importante di sviluppare la teoria delle rappresentazioni unitarie degli analoghi totalmente disconnessi dei gruppi di Lie semisemplici portandola allo stesso livello di quella dei gruppi di Lie veri e propri. Tale programma fu iniziato da F. I. Mautner nel 1958 e portato avanti da Bruhat nel 1961. Risultati completi per tutte le matrici non singolari di tipo 2 × 2 su un corpo localmente compatto e totalmente sconnesso furono ottenuti, negli anni sessanta, da Gelfand e Graev. Notevoli perfezionamenti furono apportati poco più tardi da Shalika, Tanaka e Sally. A differenza del caso dei gruppi di Lie, G può contenere sottogruppi compatti massimali non coniugati K (v. sopra, cap. 9), ma le classi di coniugio possono essere scelte canonicamente in modo che UIΚ sia privo di molteplicità. Come nel caso semisemplice, le rappresentazioni irriducibili L che compaiono nella decomposizione di UIΚ sono molto più facili da studiare che le altre. Esse hanno tutte un vettore lasciato invariato da K, che è unico a meno del prodotto per numeri complessi di modulo 1, e vengono studiate mediante le ‛funzioni sferiche' x ???14??? (Lx(ϕ)•ϕ), ove cp è un vettore lasciato invariato da K. Satake si è occupato di queste funzioni sferiche p-adiche per un G generale in un lungo lavoro pubblicato nel 1963. Pochi anni più tardi MacDonald trovò formule esplicite per le funzioni sferiche e per la misura di Plancherei per la decomposizione di UIΚ. Nelle ricerche alle quali abbiamo accennato prima, Jacquet e Langlands hanno raffinato la teoria per GL(2, F) e l'hanno rielaborata nel contesto delle rappresentazioni ‛ammissibili' in spazi vettoriali astratti. Più tardi Jacquet esaminò il modo in cui ottenere tutte le rappresentazioni irriducibili ‛ammissibili' di GL(n, F) come componenti di rappresentazioni indotte da rappresentazioni ‛supercuspidali' di sottogruppi. Le rappresentazioni supercuspidali sono gli analoghi degli elementi della serie discreta e il risultato di Jacquet è stato esteso a gruppi p-adici più generali da Harish-Chandra. Riferendosi a questo fatto come alla ‛filosofia delle forme cuspidali', Harish-Chandra ha mostrato inoltre che i metodi adoperati da Langlands nello studio di UIΚ possono applicarsi anche alla rappresentazione regolare delle versioni sia reali che p-adiche di gruppi di Lie semisemplici. In base a essa egli ha compiuto progressi significativi verso una formula di Plancherel per la rappresentazione regolare nel caso p-adico.
16. Teoria dei gruppi e fisica.
La fisica può essere considerata, in larga misura, un'estensione della geometria nella quale si studiano configurazioni spaziali che dipendono da un parametro reale chiamato ‛tempo'. Il caso più semplice è quello della ‛meccanica delle particelle', dove la configurazione da studiare è un insieme finito di punti nello spazio. Nella meccanica dei continui, d'altra parte, così come nella teoria elettromagnetica della luce e nella teoria della conduzione del calore, una configurazione è una funzione, a valori scalari o vettoriali, definita in uno spazio o in un certo sottoinsieme prefissato dello spazio. Le osservazioni sperimentali mostrano che i cambiamenti di una configurazione nel tempo, che si presentano in natura, seguono certe leggi che permettono di predire il futuro quando si abbia una conoscenza sufficientemente dettagliata del presente. In altre parole, di tutte le funzioni immaginabili, dalla retta reale allo spazio delle configurazioni possibili, soltanto un piccolo sottoinsieme si presenta effettivamente e questo sottoinsieme è tale che due elementi che coincidono localmente (o anche infinitesimamente) coincidono dappertutto. Uno degli scopi principali della fisica è quello di trovare le leggi che determinano i possibili ‛cammini nello spazio delle configurazioni' e di sviluppare tecniche di calcolo che permettano di determinare il futuro dal presente quando si conoscano le leggi. Nella meccanica delle particelle, scoperta da Newton, un cammino nello spazio delle configurazioni è determinato completamente quando si conosca la configurazione in un dato punto in un certo istante e si conosca il ‛vettore tangente' al cammino in quel punto e in quell'istante: quando si conoscano cioè le posizioni e le componenti della velocità per tutte le particelle. La coppia costituita dalla configurazione e dal ‛vettore tangente' a essa nello spazio di tutte le configurazioni si chiama ‛stato' del sistema. Naturalmente ogni cammino nello spazio delle configurazioni costituisce un cammino nello spazio degli stati e segue dalla scoperta di Newton che per ogni punto dello spazio degli stati passa al più un cammino. Sia Ω l'insieme degli stati che si presentano e, per ogni ω in Ω e ogni t > 0, indichiamo con Ut(ω) il punto nel cammino che è ω quando t = 0. Dalle definizioni segue immediatamente che Ut1+t2 = U;t1 • Ut2. Molti sistemi sono reversibili nel senso che Ut è biunivoca e surgettiva, cosicché si può definire U-t = Ut-1e si ottiene così un omomorfismo del gruppo additivo della retta nel gruppo delle trasformazioni biunivoche di Ω su se stesso. Conoscere l'omomorfismo U (chiamato talvolta ‛gruppo dinamico') equivale naturalmente a conoscere tutti i possibili cammini nello spazio delle configurazioni. È tuttavia molto raro che si riesca a descrivere questo omomorfismo in modo diretto. Si usa invece la tecnica di associare il finito all'‛infinitesimo' (inventato da Newton proprio a questo scopo) e si sposta l'attenzione da U al campo di vettori in Ω che a ogni ω in Ω associa il vettore tangente Aω nel punto ω al cammino t ???14??? Ut(ω). Quando sono soddisfatte condizioni ragionevoli di regolarità, U è determinato univocamente da questo campo di vettori, che viene chiamato il suo ‛generatore infinitesimo'. Il punto cruciale sta nel fatto che di solito si può esplicitare una formula semplice che permette il calcolo di Aω a partire da ω; questa formula è allora la legge fisica in questione. Essa specifica univocamente i possibili cammini nello spazio delle configurazioni. Trovare tali cammini e predire il futuro diventa allora il problema di risolvere un sistema di equazioni differenziali ordinarie date esplicitamente, problema che può essere affrontato, anche se di fatto è tutt'altro che banale. Considerazioni parallele possono applicarsi quando lo spazio delle configurazioni è uno spazio di funzioni a valori scalari o vettoriali definite su uno spazio fisico. S'introduce ancora uno spazio dello stato e un gruppo dinamico e si scopre che la legge fisica può essere espressa scrivendo esplicitamente un generatore infinitesimo per il gruppo dinamico. In questo caso, tuttavia, la ricerca dei cammini implica la soluzione di un sistema di equazioni alle derivate parziali. Per esempio, se lo spazio delle configurazioni è lo spazio dei possibili ‛campi elettrici' nello spazio libero, lo spazio degli stati è l'insieme di tutte le coppie E, H costituite da un campo elettrico E e da un campo magnetico H. Le equazioni differenziali alle derivate parziali sono allora le famose equazioni di Maxwell.
Sia Ω lo spazio degli stati per un sistema di particelle e sia GΩ il gruppo delle ‛trasformazioni biunivoche' di Ω su Ω che conservano le funzioni infinitamente differenziabili. Si può pensare a GΩ come a un gruppo di Lie a infinite dimensioni, la cui algebra di Lie consiste dei campi di vettori di classe C∞. La legge di composizione nell'algebra di Lie è definita in modo analogo a quella definita nel cap. 5. Si può definire lo spazio degli stati in un modo leggermente diverso, utilizzando gli elementi dello spazio duale dello spazio dei vettori tangenti in un punto invece che dei vettori tangenti stessi. Il nuovo spazio degli stati Ω′ che così si ottiene si comporta come Ω, ma la sua struttura è ulteriormente specificata, in modo molto utile, dal fatto che esiste un'applicazione canonica W che trasforma campi di vettori di classe C∞ L, M in funzioni di classe C∞; questa applicazione è antisimmetrica, lineare in ambedue le variabili e tale che
W(fL, M) = W(L, fM) = fW(L, M)
per ogni funzione f di classe C∞. W definisce un'applicazione lineare f ???14??? Lf di funzioni infinitamente differenzia- bili nei campi dei vettori, in modo tale che Lf= 0 se, e soltanto se, f è costante. Il rango di questa applicazione è una classe di campi di vettori la quale gode dell'utile proprietà di essere completamente definita dalla singola funzione f. Quando il generatore infinitesimo del gruppo dinamico è del tipo LH per un certo H, si dice che il sistema dinamico è un sistema bamiltoniano e che H (determinato a meno di una costante additiva) è l'hamiltoniano del sistema. Il valore di H nello stato ω viene chiamato energia del sistema in tale stato. Se f è una funzione di classe C∞ in Ω′, W(LA, Lf) è la funzione che fornisce la derivata di flungo le orbite del gruppo dinamico. Quando f = H, l'antisimmetria di W implica che W(LH, Lf) = 0, cosicché f = H è costante sulle orbite. Nell'ambito ditale contesto, questa è la legge di conservazione dell'energia. Più in generale, sia t ???14??? Vt un qualsiasi gruppo a un parametro di automorfismi di Ω′. Se esso conserva W, si può dimostrare che il suo generatore infinitesimo è del tipo L῍. Se esso è un gruppo a un parametro di simmetrie del sistema, nel senso che lascia invariante H, risulta W(L῍, LH) = 0. Ma, in virtù dell'antisimmetria, si ha W(LH, L῍) = 0, così che ϕ è costante sulle orbite del gruppo dinamico. Pertanto (a meno di costanti additive) si ha una corrispondenza biunivoca naturale tra gruppi a un parametro di simmetrie e funzioni su Ω′ che sono costanti rispetto al tempo. Ora, le funzioni su Ω′ che sono ‛conservate' (che sono cioè costanti nel tempo) si chiamano ‛integrali di moto'. La conoscenza di una di esse semplifica il problema della determinazione delle orbite, riducendolo a un problema di dimensione inferiore. La corrispondenza ora descritta mostra come la simmetria nelle equazioni di moto può essere utilizzata per risolvere il problema della loro integrazione. In generale, la funzione W(Lf, Lg) viene chiamata ‛parentesi di Poisson' delle funzioni f e g. Qualsiasi gruppo a un parametro di automorfismi di uno spazio fisico induce in modo naturale un gruppo a un parametro di automorfismi di Ω′ e, quando l'interazione fra le particelle è indipendente dalla posizione e dall'orientazione nello spazio, questo gruppo a un parametro è un gruppo di simmetrie. In questo modo ogni gruppo a un parametro di automorfismi spaziali è canonicamente associato a un integrale di moto. È lecito attendersi che questi integrali svolgano un ruolo essenziale e di fatto avviene proprio così. Essi vengono chiamati ‛integrali del momento'. Nel modello euclideo usuale dello spazio, il gruppo degli automorfismi è di dimensione 6 e si hanno corrispondentemente sei integrali indipendenti del momento. Quelli associati a gruppi a un parametro di traslazioni si chiamano ‛integrali del momento lineare'; quelli associati a gruppi a un parametro di rotazioni si chiamano ‛integrali del momento angolare'. Naturalmente le leggi di conservazione degli integrali del momento lineare o angolare erano noti molto prima che venisse posto in luce il loro significato gruppale.
Le considerazioni alle quali abbiamo ora accennato possono essere applicate anche quando lo spazio delle configurazioni è uno spazio di funzioni a valori scalari o vettoriali. Inoltre nell'importante (sebbene in gran parte idealizzato) caso particolare in cui il generatore infinitesimo A di t ???14??? Ut è una trasformazione lineare, le implicazioni della simmetria risultano molto profonde. Il fatto è che questo generatore infinitesimale risulta di solito essere estendibile a un operatore antiaggiunto rispetto a un prodotto interno in uno spazio di Hilbert in un opportuno completamento dello spazio delle fasi. Quando ciò accade, risulta Ut = eAt e si può trovare eAt non appena si conosca la risoluzione spettrale dell'operatore autoaggiunto iA. Se esiste una base ortonormale ϕ1, ϕ2, ... per lo spazio di Hilbert tale che iA(ϕj) =λjϕj, si ha
Ut(ϕj) = e-iλjt
e, per una qualsiasi ψ, risulta
Un procedimento analogo, ma più complicato, può essere sviluppato quando A ha uno spettro continuo. Naturalmente la ricerca della risoluzione spettrale di un operatore in uno spazio di dimensione infinita non è un problema banale ed è a questo punto che interviene la teoria dei gruppi. Ogniqualvolta il problema è invariante rispetto agli automorfismi dello spazio, si avrà una rappresentazione unitaria del gruppo di automorfismi α ???14??? Wα mediante operatori nello spazio degli stati, in modo tale che tutti i Wα commutino con A. Questo implica che la decomposizione canonica di W in rappresentazioni fattori disgiunte è tale che le componenti sono A invarianti e pertanto la decomposizione della rappresentazione W del gruppo determina tutta, o quasi tutta, la risoluzione spettrale di A. Quando W è priva di molteplicità si ha di fatto la risoluzione completa. Con il modello euclideo abituale per lo spazio, la restrizione di W al sottogruppo delle traslazioni risulta sempre essere una somma diretta di un numero finito di repliche della rappresentazione regolare e la decomposizione della rappresentazione regolare del gruppo delle traslazioni compie gran parte della risoluzione spettrale di A. Come abbiamo osservato nel cap. 14, la rappresentazione regolare di un gruppo commutativo viene decomposta dalla trasformazione di Fourier. Applicando i procedimenti precedenti, restringendo W al gruppo delle traslazioni, si ottengono risultati identici a quelli ottenuti in fisica dagli usuali metodi basati sulla trasformazione di Fourier. In sostanza, le considerazioni precedenti sono una spiegazione sofisticata, nell'ambito della teoria dei gruppi, del perché le trasformazioni di Fourier sono efficaci. Tuttavia tali considerazioni hanno inoltre il vantaggio di essere applicabili ad altri modelli omogenei dello spazio, ove l'analogo del sottogruppo delle traslazioni non è commutativo. L'utilità delle serie di Fourier per problemi su intervalli e delle serie di Fourier multiple per problemi su parallelepipedi rettangolari ha una spiegazione analoga, nella quale il gruppo delle traslazioni è sostituito da uno dei suoi gruppi quozienti compatti.
In quanto abbiamo detto sopra, si è tacitamente convenuto che lo spazio fisico fosse un'entità fissa ben definita. Tuttavia, prendendo in considerazione il modello euclideo, un osservatore che si muova verso un altro con una velocità uniforme fissata non vedrà affatto lo stesso spazio. Ciò che per uno è un punto fisso dello spazio parrà all'altro un continuo lineare di punti distinti. Se si sapesse come definire l'immobilità assoluta si potrebbero definire i punti dello spazio come quelli che sono visti da un osservatore immobile. Ma tale definizione è tutt'altro che facile. Le leggi della meccanica delle particelle sono tali che gli osservatori che si muovono uniformemente l'uno rispetto all'altro rilevano le stesse leggi, riferite ai loro spazi personali. Per l'osservatore A le particelle a ogni istante hanno velocità diverse da quelle che esse hanno per l'osservatore B. Tuttavia A vede lo stesso futuro di B, quando le particelle hanno per A velocità relative uguali a quelle che hanno per B. D'altra parte, le equazioni di Maxwell che controllano la propagazione delle onde elettromagnetiche nello spazio non sono invarianti in questo modo e si è ritenuto per un certo tempo che misure accurate della velocità di propagazione di tali onde (la velocità della luce) in direzioni diverse sarebbero state sufficienti a determinare lo stato di moto assoluto di un osservatore. Tuttavia, il famoso esperimento di Michelson e Morley del 1887 mostrò che la velocità della luce relativa alla Terra è la stessa in tutte le direzioni, indipendentemente dalla posizione della Terra nella sua orbita intorno al Sole. Molte furono le spiegazioni offerte per questo apparente paradosso, ma quella che viene oggi comunemente accettata è quella proposta da Einstein nel 1905. Era stato precedentemente accertato da Poincaré e Lorentz che le equazioni di Maxwell sono invarianti per trasformazioni di coordinate rispetto a un sistema di riferimento che si muove con moto uniforme, purché la legge di trasformazione ‛ingenua' x′ = x − vt, t′ = t venga sostituita dalle
ove c è la velocità della luce. Einstein scoprì che si poteva trovare una giustificazione razionale per l'uso di questa legge di trasformazione modificata, analizzando accuratamente cosa significa confrontare misure di tempo fatte da osservatori che si muovono l'uno rispetto all'altro. Egli arrivò alla conclusione che porre t′ = t è del tutto arbitrario e che la nozione di simultaneità ha un significato chiaro solo nell'ambito di un dato sistema di riferimento. Il concetto di tempo assoluto è altrettanto dubbio di quello di spazio assoluto e soltanto lo spazio-tempo ha un significato assoluto. Per spazio-tempo s'intende l'insieme delle coppie costituite da un punto dello spazio e un punto del tempo. Ogni punto dello spazio-tempo corrisponde, per un osservatore, a un unico punto dello spazio-tempo di un altro (che si muove uniformemente rispetto al primo). La proposta di Einstein, che risultò poi avere conseguenze profondamente rivoluzionarie, può essere formulata in modo molto succinto nell'ambito della teoria dei gruppi. Essa dice di fatto che il gruppo degli automorfismi dello spazio-tempo è diverso da quanto si è sempre ritenuto. Le traslazioni dello spazio-tempo formano un sottogruppo normale in ambedue i casi, ma il gruppo degli automorfismi che lascia invariato un punto non è il gruppo generato dalle rotazioni spaziali e dalle trasformazioni del tipo
x, y, z, t ???14??? x − vt, y, z, t.
Esso è invece il cosiddetto ‛gruppo di Lorentz', generato dalle rotazioni spaziali e dalle trasformazioni del tipo
Il gruppo generato dal gruppo di Lorentz e dalle traslazioni nello spazio-tempo è il prodotto semidiretto di questi due gruppi e viene chiamato ‛gruppo di Poincaré'. Il gruppo che esso sostituisce prende il nome di ‛gruppo di Galileo'. Il gruppo di Lorentz risulta essere isomorfo al quoziente di SL(2, C) per i suoi due elementi centrali ed è pertanto un gruppo di Lie semisemplice. Il gruppo di Galileo è anch'esso un prodotto semidiretto di un gruppo vettoriale a quattro dimensioni e di un gruppo non commutativo a sei dimensioni. Ora però il gruppo a sei dimensioni è un prodotto semidiretto di un gruppo vettoriale di dimensione 3 e di un gruppo compatto e non è semisemplice. Esso è di fatto isomorfo al gruppo generato dalle traslazioni e dalle rotazioni nello spazio fisico. Il gruppo di Galileo sostiene in fisica un ruolo importante, malgrado le scoperte di Einstein; ciò accade perché la ricerca delle leggi fisiche invarianti per il gruppo di Galileo è molto più facile di quella delle leggi invarianti per il gruppo di Poincaré e il gruppo di Galileo costituisce un'approssimazione molto buona in situazioni particolarmente importanti.
Come abbiamo spiegato dianzi, attraverso le leggi di conservazione e l'ampio uso delle serie e degli integrali di Fourier, le idee della teoria dei gruppi sono state presenti nella fisica per molto tempo. Tuttavia, a eccezione che nella classificazione dei cristalli ricordata nell'introduzione, i fisici fecero pochissimo uso della teoria dei gruppi fino a che, poco prima del 1930, non cominciarono ad apprezzarne l'estrema utilità nella meccanica quantistica, a quell'epoca appena scoperta. Tuttavia anche allora si manifestò tra i fisici una violenta reazione contro ‛l'inquinamento gruppale', concetto del tutto estraneo alla fisica, e si dovette aspettare la nuova generazione perché la concezione gruppale venisse pienamente accettata. L'uso del gruppo di Lorentz e del concetto d'invarianza di Lorentz, tra il 1905 e il 1925, può apparire come un'eccezione, ma nelle prime esposizioni delle idee di Einstein la teoria dei gruppi è tenuta molto sullo sfondo e tali esposizioni possono essere comprese persino senza conoscere la definizione di gruppo.
Per molto tempo uno degli scopi della fisica è stato quello di spiegare tutti i fenomeni fisici a partire dai movimenti delle particelle ‛elementari' o ‛fondamentali' che costituiscono la materia. Tuttavia, le scoperte di Planck, Einstein, Bohr e altri, nei primi tre lustri del nostro secolo, suscitarono seri dubbi sulla realizzabilità di tale programma. A quell'epoca si poté finalmente operare direttamente sugli atomi, sui nuclei e sugli elettroni e questi sembravano comportarsi in un modo assolutamente incomprensibile nell'ambito della meccanica newtoniana. Di volta in volta si riusciva a ‛spiegare' uno specifico fenomeno atomico soltanto sovrapponendo alle leggi della meccanica delle ‛regole di quantizzazione', adattate al fenomeno in questione in un modo misterioso e logicamente incoerente. Si rendeva chiaramente necessaria una revisione drastica dei concetti fondamentali e tale revisione fu effettuata con l'introduzione della meccanica quantistica tra il 1920 e il 1930. Fra il 1924 e il 1925, W. Heisenberg e E. Schrödinger pubblicarono, rispettivamente, lavori che a un'indagine superficiale apparivano molto distinti e che fornivano la chiave del mistero. Seguì un eccitante periodo di frenetica attività, al quale parteciparono molti scienziati, in particolare Schrödinger, Heisenberg, M. Born, H. Bohr, P.A.M. Dirac e il matematico J. von Neumann. Non è facile ripercorrere il corso degli eventi, ma alla fine del 1927 la meccanica classica è stata sostituita da una nuova teoria, assai più sottile, che spiega le regole della quantizzazione, ammette la meccanica classica come un'ottima approssimazione per particelle di massa notevole e si è dimostrata capace di raggiungere profondi risultati per quanto riguarda la spiegazione della struttura e delle proprietà della materia in funzione dei suoi costituenti fondamentali e delle loro interazioni. L'idea base è che le misure di velocità e di posizione interferiscono l'una con l'altra in modo tale che, in linea di principio, non ha senso parlare di una particella che abbia in uno stesso istante una certa velocità ‛esatta' e una certa posizione ‛esatta'. Il grado d'interferenza è inversamente proporzionale alle masse delle particelle che si considerano e ha effetti sensibili soltanto per particelle della dimensione di un atomo. D'altra parte, si può invece parlare delle distribuzioni simultanee di probabilità degli osservabili, per i quali non si possono definire i valori esatti, e il cambiamento concettuale fondamentale per passare dalla meccanica classica alla meccanica quantistica è che si guarda ora alle ‛equazioni di moto' come a qualcosa che permette di predire probabilità future a partire da probabilità passate piuttosto che valori futuri esatti a partire da valori passati esatti. La formulazione rigorosa del meccanismo matematico che attua queste predizioni è dovuta a von Neumann; essa fa intervenire il teorema spettrale in un modo essenziale. Questo teorema, che è stato indirettamente descritto nel cap. 8, stabilisce una corrispondenza biunivoca tra tutti gli operatori autoaggiunti in un dato spazio di Hilbert separabile e tutte le misure a valori proiettori (v. sopra, cap. 8) definite sulla retta reale. La corrispondenza è tale che quando T e E ???14??? PE si corrispondono, risulta
(T(f)•f) = ∫ xdαf(x)
ogniqualvolta T(f) è definito. Qui αf è la misura E ???14??? (PE(f)•f). Si può allora descrivere nel modo seguente la formulazione di von Neumann: si sostituisce allo spazio degli stati Ω′ del sistema classico l'insieme di tutti i sottospazi a una dimensione di un opportuno spazio di Hilbert ℋ. Si associa a ogni osservabile (cioè coordinata di posizione, coordinata di velocità o funzioni significative di queste variabili) un operatore autoaggiunto A. Sia E ???14??? PAE la misura a valore proiettore sulla retta reale associata canonicamente ad A dal teorema spettrale. Per ogni vettore unitario ϕ in ℋ, E ???14??? (PE(ϕ)•ϕ) è una misura di probabilità che dipende soltanto dal sottospazio a una dimensione al quale appartiene ϕ. Essa è la distribuzione di probabilità che la teoria fa corrispondere all'osservabile associato ad A quando esso appartiene allo stato associato al sottospazio a una dimensione dei multipli di ϕ. Se ϕ definisce lo stato del sistema in un certo punto nel tempo, t unità di tempo più tardi esso è definito da e-iHtϕ, ove H è un operatore autoaggiunto fisso il quale sostiene nella meccanica quantistica il ruolo che nella meccanica classica ha la funzione hamiltoniana. Una descrizione completa di un sistema in meccanica quantistica si ottiene assegnando uno spazio di Hilbert concreto, stabilendo la corrispondenza tra operatori e osservabili e specificando l'operatore dinamico H. È chiaro che in ogni stato è nulla la probabilità che l'osservabile associato all'operatore autoaggiunto assuma valori fuori dallo spettro di A. Le regole di quantizzazione della vecchia teoria quantistica appaiono nella meccanica quantistica come conseguenze del fatto che certi osservabili risultano associati a operatori aventi spettri discreti.
In termini generali, l'importanza della teoria dei gruppi per la meccanica quantistica è la stessa che nella meccanica classica. Si ha un gruppo dinamico t ???14??? Ut = e-iHt il cui generatore infinitesimo −iH è associato con un osservabile chiamato energia. Inoltre la corrispondenza fra certi gruppi a un parametro di automorfismi di Ω′ e gli osservabili di classe C∞ equivale, nella meccanica quantistica, alla corrispondenza stabilita dal teorema di Stone (v. sopra, cap. 8) tra gli operatori autoaggiunti A e le rappresentazioni unitarie della retta t ???14??? e-iAt. Un analogo della parentesi di Poisson è fornita dal commutatore i(HA − AH) e, come nella meccanica classica, il gruppo a un parametro t ???14??? e-iAt lascia H invariato se, e soltanto se, l'osservabile corrispondente ad A è un integrale di moto. In questo caso, che l'osservabile corrispondente ad A sia un integrale di moto significa che la misura di probabilità definita in ogni stato è costante nel tempo. In particolare, esistono in meccanica quantistica gli osservabili momento angolare e momento lineare ed essi sono associati a generatori infinitesimi di gruppi a un parametro di traslazioni e rotazioni. Il fatto che il momento angolare sia sempre ‛quantizzato' nella meccanica quantistica dipende dalla compattezza dei gruppi di rotazione a un parametro. Una differenza importante sta nel fatto che in meccanica quantistica lo spazio degli stati è (essenzialmente) uno spazio di Hilbert anche per un sistema di particelle e il generatore infinitesimo del gruppo dinamico è il prodotto di i per un operatore autoaggiunto. Pertanto i metodi della teoria dei gruppi, che nella meccanica classica sono efficaci soltanto per sistemi piuttosto particolari propagazione di onde elastiche ed elettromagnetiche ecc. - sono invece universalmente efficaci nella meccanica quantistica. Si può sempre trovare Ut e integrare le equazioni di moto ogniqualvolta sia possibile determinare la decomposizione spettrale di H, ricorrendo ai gruppi di simmetria per collegare tale decomposizione spettrale all'analisi delle componenti irriducibili di certe rappresentazioni di questi gruppi. Quando si considera una sola particella libera, le conseguenze dell'invarianza per traslazioni si possono ottenere mediante l'analisi di Fourier, come nella teoria classica dei sistemi vibranti, e si può in tal caso evitare l'uso esplicito della teoria dei gruppi. Tuttavia, nello studio della meccanica quantistica di un atomo che s'immagina costituito da un ‛nucleo' circondato da n elettroni identici, i gruppi di simmetria importanti sono i gruppi di rotazioni intorno al nucleo e il gruppo di tutte le permutazioni degli n elettroni. Questi gruppi sono non commutativi e la teoria delle loro rappresentazioni irriducibili deve sostituire l'uso implicito dei caratteri a una dimensione che compare nell'analisi di Fourier. Il fatto che la teoria delle rappresentazioni dei gruppi potesse essere utile nello studio della meccanica quantistica di un atomo fu notato per la prima volta da E. P. Wigner in un volume della Zeitschrift für Physik che apparve nel 1926-1927. Lo studio degli autovalori di H in questo caso è estremamente complicato e si ricorre alla teoria delle perturbazioni cominciando a considerare un'approssimazione H0 di H che trascura le interazioni mutue fra gli elettroni. Gli autospazi e gli autovalori di H0 sono relativamente facili da determinare e si passa all'approssimazione successiva diagonalizzando le proiezioni di H − H0 in questi autospazi. Si ha una rappresentazione naturale del gruppo Sn di tutte le permutazioni degli elettroni su ciascun autospazio e la proiezione di H − H0 è l'algebra commutante della rappresentazione. Wigner applicò il principio generale che abbiamo indicato dianzi, secondo il quale una riduzione di una rappresentazione di un gruppo in sottorappresentazioni disgiunte implica una corrispondente riduzione di ciascun operatore nella sua algebra commutante. Più precisamente, egli affrontò il problema di diagonalizzare tanti operatori quante sono le componenti irriducibili non equivalenti della rappresentazione - la dimensione di ciascun operatore ridotto essendo la molteplicità con cui appare la rappresentazione irriducibile associata. Non molto tempo dopo, Wigner applicò le sue idee al gruppo delle rotazioni (si ricordi che H0 commuta con una rappresentazione del prodotto di n copie del gruppo delle rotazioni con se stesso. Ulteriori contributi furono apportati da von Neumann e da altri. A questo punto, nel 1928, H. Weyl pubblicò un notevole trattato: Gruppentheorie und Quantenmechanik. In quest'opera, ormai divenuta un classico, Weyl fornì una presentazione unificata delle idee di Wigner e di altri, inserendole in un'esposizione sistematica della teoria delle rappresentazioni dei gruppi e della meccanica quantistica. Egli riuscì a mettere in luce il fatto che la teoria dei gruppi è molto più che un utile artificio per semplificare il problema della diagonalizzazione delle matrici. Essa è di fatto uno strumento concettuale che permette una visione assai profonda, nella teoria della meccanica quantistica, della struttura della materia. Anche Wigner scrisse un libro su questo argomento (1931), ma si limitò essenzialmente a esaminare in dettaglio le applicazioni delle rappresentazioni di Sn e del gruppo delle rotazioni alla teoria degli spettri atomici. A quest'opera, tuttavia, Wigner fece seguire una serie di lavori pionieristici, nei quali mostrò come la teoria delle rappresentazioni dei gruppi potesse essere efficacemente applicata a svariati rami della fisica quantistica. Un lavoro sulle applicazioni alla teoria quantistica dei solidi (scritto in collaborazione con L. P. Bouckaert e R. Smoluchowski) comparve nel 1936, uno sulle applicazioni alla struttura dei nuclei atomici nel 1937 e infine uno sulle particelle relativistiche libere fu pubblicato nel 1939. I gruppi presi in esame erano i gruppi cristallografici, il gruppo compatto [SO(4)]n e il gruppo di Poincaré. Nel suo lavoro del 1939, Wigner introdusse il principio secondo cui lo spazio di Hilbert degli stati di una particella relativistica libera è, in modo naturale, lo spazio di Hilbert di una rappresentazione unitaria (proiettiva) irriducibile del gruppo di Poincaré e secondo cui è possibile classificare le particelle classificando la rappresentazione irriducibile. Egli affrontò quindi il problema di classificare le rappresentazioni e vi riuscì nella misura in cui intervengono quelle che hanno ‛significato fisico'. La determinazione delle altre era fatta a meno della determinazione delle rappresentazioni unitarie irriducibili del gruppo di Lorentz e del suo equivalente nello spazio-tempo a tre dimensioni, cioè dei quozienti di SL(2, C) e SL(2, R) per i loro centri. Questo lavoro di Wigner ebbe enorme importanza nello sviluppo successivo della teoria delle rappresentazioni unitarie. Per la prima volta si disponeva di un'analisi delle rappresentazioni unitarie irriducibili di un gruppo per il quale tali rappresentazioni irriducibili hanno ‛dimensione infinita'. inoltre, questo lavoro stimolò Gelfand e Neumark da una parte e V. Bargmann dall'altra nelle loro ricerche volte a determinare le rappresentazioni unitarie irriducibili di SL(2, C) e SL(2, R) e a porre così, nel 1946, i fondamenti della teoria delle rappresentazioni unitarie dei gruppi di Lie semisemplici non compatti.
Nell'impostazione di Heisenberg della meccanica quantistica un ruolo fondamentale è sostenuto dall'ipotesi secondo la quale gli operatori Q1, Q2, ..., Q3n e P1, P2, ..., P3n corrispondenti alle coordinate e ai momenti di un sistema di n particelle soddisfano le famose ‛regole di commutazione di Heisenberg'. Secondo queste, i Pj commutano fra loro, altrettanto fanno i Qj, mentre QjPk − PkQj = 0 oppure (ih/2π)I a seconda che j ≠ k o j = k. I è l'operatore identità e h è la costante fondamentale introdotta da Planck. Nella misura in cui l'operatore hamiltoniano H può essere espresso in funzione dei Qj e Pk, un teorema di unicità per gli operatori che soddisfano le regole di commutazione di Heisenberg implica un teorema di unicità per l'intero modello quantistico. È difficile formulare tale teorema di unicità in termini rigorosi, a causa del significato ambiguo del commutatore di due operatori non limitati e, per conseguenza, definiti solo densamente. Tuttavia, come fu messo in rilievo da Weyl nel libro al quale abbiamo precedentemente accennato, si possono sostituire i Qj e i Pk con due rappresentazioni unitarie
q = q1, q2, ..., q3n ???14??? Uq = eiq1Q1eiq2Q2...eiq3nQ3n
e
p = p1, p2, ..., p3n ???14??? Vp = eip1P1eip2P2...eip3nP3n,
ove q e p sono elementi del gruppo additivo delle 3n-uple di numeri reali. La commutatività dei Qj fra loro e dei Pk fra loro è contenuta nell'affermazione secondo cui U e V sono rappresentazioni di un gruppo commutativo, mentre le rimanenti regole di Heisenberg sono equivalenti, a un livello formale, all'affermazione secondo cui
UqVp = e-i(p∣q)VpUq
per tutti i p e i q, ove
A questo punto si può dimostrare un teorema rigoroso secondo cui, a meno di un'equivalenza unitaria, esiste una e una sola soluzione irriducibile delle relazioni di Weyl. Questo risultato fu annunciato da R. H. Stone nel 1930 e una dimostrazione completa fu pubblicata da von Neumann nel 1931. Von Neumann provò anche che ogni soluzione è una somma discreta di soluzioni irriducibili. Le relazioni di Weyl possono essere espresse in una forma che ha un significato più generale, poiché q ???14??? e-i(p∣q) è proprio il carattere più generale di dimensione 1 nel gruppo delle q, e si possono considerare U e V come rappresentazioni unitarie di un gruppo commutativo e del suo gruppo dei caratteri, rispettivamente. Sia G un arbitrario gruppo commutativo localmente compatto e separabile e sia Ø il suo gruppo dei caratteri. Sia μ una misura di Haar in G e siano U e V le rappresentazioni unitarie, rispettivamente, di G e Ø, definite in ℒ2(G, μ) ponendo Uxf(y) = f(yx) e Vχf(y) = χ(y)•f(y). Si verifica immediatamente che UxVχ = χ(x)VχVx per tutti gli x e tutti i χ e che questa identità si riduce alle relazioni di Weyl quando G è uno spazio vettoriale reale. Vale il teorema di unicità più generale ed esso può essere dimostrato usando il teorema spettrale per le rappresentazioni, dei gruppi commutativi (v. sopra, cap. 8) per sostituire V con la misura a valori proiettori associata, P, su Ø = G. Espresse in termini di U e P, le relazioni di Weyl per U e V diventano
PEUx = P[E]x-1Ux.
In altre parole esse affermano semplicemente che P è un sistema di imprimitività (v. sopra, cap. 8) per U di base G e l'unicità richiesta segue subito dal teorema di imprimitività. Infatti, in questo caso, il sottogruppo H in G/H si riduce a un solo elemento e ha una e una sola rappresentazione irriducibile. Questo caso particolare del teorema di imprimitività fu usato per la prima volta come generalizzazione non commutativa dell'unicità delle regole di commutazione di Heisenberg, mentre il teorema di imprimitività propriamente detto venne dimostrato molti mesi più tardi come ulteriore generalizzazione. La generalizzazione del teorema di Stone a un teorema spettrale per rappresentazioni unitarie di gruppi commutativi fu compiuta indipendentemente da Ambrose, Godement e Neumark fra il 1943 e il 1944. La sua applicazione al teorema generalizzato di unicità di Stone-von Neumann e l'enunciato e la dimostrazione, del teorema di imprimitività furono opera di G. W. Mackey, che pubblicò i suoi risultati nel 1949. Come abbiamo detto nel cap. 8, il teorema generale sulle rappresentazioni unitarie irriducibili dei prodotti semidiretti è un corollario del teorema spettrale e del teorema di imprimitività. Poiché i risultati di Wigner sul gruppo di Poincaré sono corollari del teorema generale sui prodotti semidiretti, si ha un secondo legame del teorema di imprimitività con la fisica. Un altro ancora è stato trovato da Wightman all'inizio degli anni cinquanta, ma non è stato pubblicato fino al 1962. Wightman osservò che un'analisi del concetto di ‛osservabile di posizione' per una particella relativistica, introdotto da Wigner e T. D. Newton nel 1949, poteva essere esposta in forma rigorosa usando il teorema di imprimitività. Ricorrendo a idee strettamente connesse a quelle di Newton, Wigner e Wightman, si può dare una esposizione assiomatica della nozione di particella in meccanica quantistica, nella quale le regole di commutazione di Heisenberg divengono un teorema piuttosto che un assioma e nella quale la nozione di spin di una particella interviene in modo naturale. Indichiamo con S uno spazio fisico e sia ℰ il gruppo delle isometrie di S. Sia ℋ lo spazio di Hilbert degli stati di un sistema ridotto a una particella e indichiamo con α ???14??? Ux la rappresentazione unitaria (eventualmente proiettiva) di ℰ che riflette il fatto che le leggi di movimento sono ℰ-invarianti. Per ogni sottoinsieme di Borel E di S sia PE l'operatore di proiezione corrispondente all'osservabile che è 1 quando la particella sta in E e 0 altrimenti. Si può allora osservare che E ???14??? PE deve essere una misura a valori proiettori e che la conoscenza di tale misura è equivalente a quella dell'operatore autoaggiunto associato a ogni coordinata a valori reali in S. Una semplice analisi del significato d'invarianza conduce alla conclusione che
UxPEUx-1 = P[E]α-1
per tutti gli E e α; in altre parole, P è un sistema di imprimitività per U di base S. Il teorema di imprimitività fornisce allora una determinazione completa di tutte le coppie U, P, a meno di un'equivalenza unitaria. Esse sono parametrizzate dalle rappresentazioni unitarie del sottogruppo R di ℰ che lascia un'origine s0 invariata. Ogniqualvolta la rappresentazione unitaria di R che interviene è diversa dall'identità, la particella ha un momento angolare addizionale che non ha niente a che fare con il suo movimento nello spazio e può ritenersi dovuto a uno spin attorno al suo ‛centro'. Ciascuna particella in natura è associata a una rappresentazione definita di R e, quando R = SO(3) (come accade nel modello euclideo usuale dello spazio), una particella di spin j è una particella per la quale questa rappresentazione è Dj, cioè l'unica rappresentazione proiettiva irriducibile di dimensione 2j + 1 di SO(3). Naturalmente lo spin non è stato scoperto mediante quest'analisi. L'ipotesi che un elettrone debba avere un momento angolare intrinseco era stata avanzata nel 1925 da S. A. Goudsmit, G. E. Uhlenbeck e W. Pauli per spiegare certi fenomeni misteriosi negli spettri atomici. Il fatto che un elettrone abbia spin 1/2 piuttosto che 0 significa che lo spazio di Hilbert degli stati consiste di funzioni a valori vettoriali bidimensionali su S piuttosto che di funzioni a valori complessi e pertanto ‛raddoppia' il numero degli stati possibili. Questo raddoppio ha molte conseguenze importanti. Una di queste è che i periodi nella ben nota tavola periodica della chimica sono 2, 8, 18 e 32 e non 1, 4, 9 e 16, come sarebbero se l'elettrone avesse spin 0. I numeri 1, 4, 9, 16, ... sono le somme 1, 1 + 3, 1 + 3 + 5 delle dimensioni di quelle rappresentazioni unitarie irriducibili di SO(3) che si presentano nella rappresentazione derivata dall'azione naturale di SO(3) sulla superficie della sfera unità. Il fatto che gli elementi mostrino la periodicità indicata simbolicamente nelle tavole periodiche è una conseguenza dell'invarianza rispetto alle rotazioni e del principio, che ora esporremo, noto come principio di esclusione di Pauli.
Prendendo come punto di partenza l'assiomatica della cinematica delle particelle che abbiamo appena delineato, si può costruire un modello matematico per la struttura della materia in cui i concetti e i problemi di maggior rilievo appartengono alla teoria delle rappresentazioni unitarie dei gruppi. La dinamica di un sistema costituito da una particella è definita da una rappresentazione unitaria t ???14??? Ut della retta reale, che, per l'invarianza, deve essere tale che VtUx = UαVt per tutti i t e tutti gli α. Quindi U e V determinano, e ne sono a loro volta determinate, la rappresentazione proiettiva unitaria α, t ???14??? UαVt del prodotto diretto ℰ × T di ℰ per il gruppo di traslazione temporale. Corrispondentemente, si può ‛definire' come particella il sistema costituito da una rappresentazione proiettiva unitaria di ℰ × T insieme a un sistema di imprimitività per la sua restrizione a ℰ × e avente per base l'ℰ-spazio S. L'ipotesi dell'invarianza spazio-temporale conduce alla conclusione che α, t ???14??? UαVt deve essere la restrizione a ℰ × T di una rappresentazione proiettiva unitaria di un opportuno gruppo di automorfismi spazio-temporali e risulta che, ogniqualvolta la rappresentazione di R che induce L è irriducibile, la rappresentazione del gruppo degli automorfismi spazio-temporali è anch'essa irriducibile. Nel caso del gruppo di Poincaré si giunge così al principio di Wigner che associa una rappresentazione unitaria irriducibile di questo gruppo a una particella relativistica e si trova un principio analogo per l'invarianza galileana. In ambedue i casi l'intero sistema è determinato dallo spin a meno di un parametro reale, che s'identifica con la massa della particella. Nel caso di massa zero, sorgono delle difficoltà che tuttavia qui noi trascureremo. Se ℋ1 e ℋ2 sono gli spazi di Hilbert degli stati di due sistemi quantistici, lo spazio di Hilbert degli stati per il ‛sistema composto' è proprio il prodotto tensoriale ℋ1 ⊗ ℋ2 definito nel cap. 8. Se t ???14??? V¹t e t ???14??? V²t sono rappresentazioni unitarie del gruppo delle traslazioni temporali, V1 × V2 ristretta alla ‛diagonale' di T definisce una dinamica per il sistema composto, nella quale ciascuna componente si comporta come se l'altra non fosse presente. Per definire un'‛interazione' tra i sistemi bisogna specificare, e fare effettivamente operare, un altro gruppo dinamico t ???14??? V0t.
Se V0t = e-iH0t, V¹t = e-iH1t, V²t = e-iH2t, allora, a meno di difficoltà relative ai domini di operatori illimitati, H0, e quindi V0, è determinata non appena è nota J = H0 − (H1 × I) + (I × H2). L'interazione si descrive specificando J, la quale, naturalmente, deve essere determinata sperimentalmente. Quando i sistemi componenti sono particelle invarianti per il gruppo di Galileo, si possono indicare degli assiomi plausibili, i quali implicano che ogni interazione, che si presenta effettivamente, deve commutare con le misure a valori proiettori che definiscono gli osservabili di posizione delle due particelle; tale interazione deve commutare anche con la rappresentazione del gruppo di Galileo G, ottenuta restringendo alla diagonale di G × G il prodotto tensoriale delle rappresentazioni che definiscono le due particelle. I teoremi generali nella teoria delle rappresentazioni dei gruppi permettono di determinare tutte queste interazioni. Quando le due particelle sono prive di spin, le possibilità corrispondono in modo biunivoco alle funzioni a valori reali della distanza tra le particelle e possono essere identificate con le interazioni classiche del tipo ‛forze centrali'. Per particelle dotate di spin, si trovano varie altre possibilità che non si possono descrivere così facilmente, ma che conducono alle interazioni di tipo tensoriale e dipendenti dallo spin che si presentano nella fisica nucleare. Si può procedere in modo analogo anche per sistemi di più particelle servendosi di prodotti tensoriali ripetuti e del fatto che (ℋ1 ⊗ ℋ2) ⊗ ℋ3 e ℋ1 ⊗ (ℋ2 ⊗ ℋ3) sono canonicamente isomorfi. Le interazioni più importanti fra n particelle sono quelle che sono somme (in senso più o meno ovvio) di [n(n − 1)]/2 interazioni di due particelle, una per ogni coppia nel sistema di n particelle. Inoltre, tra le particelle fondamentali che costituiscono la materia, vi sono relativamente pochi ‛tipi di particelle'. In gran parte esse sono ‛repliche identiche' di altre particelle e i dati pratici a partire dai quali si costruisce un modello matematico per la struttura della materia consistono di: a) le masse e gli spins dei ‛tipi di particelle'; b) la forma dell'interazione J per ogni coppia di tipi di particelle. Assegnato il numero di volte in cui ogni tipo di particella appare e assegnati gli opportuni operatori d'interazione, si scrive il prodotto tensoriale degli spazi corrispondenti alle singole particelle, si aggiungono le interazioni fra le varie coppie di particelle alla somma degli hamiltoniani per le singole particelle e si ottiene quasi il modello quantistico per il sistema delle particelle interagenti tra loro. Tuttavia, bisogna fare un altro passo tutte le volte che si presentano almeno due repliche dello stesso tipo di particella. Precisamente, si deve sostituire il prodotto tensoriale ℋ1 ⊗ ℋ2 ... ⊗ ℋn con un suo sottospazio relativamente piccolo. Si scrive
ℋ1 ⊗ ℋ2 ... ⊗ ℋn
come
ℋ11 ⊗ ℋ12 ... ⊗ ℋ1n ⊗ ℋ21 ⊗ ℋ22 ...,
ove ℋjk e ℋjk′ sono spazi di Hilbert per repliche dello stesso tipo di particella. Il gruppo delle permutazioni di nj oggetti agisce in modo naturale su
ℋj1 ⊗ ℋj2 ... ⊗ ℋjn,
per ogni j, e si possono mettere in evidenza due sottospazi. Uno di questi, detto ‛sottospazio simmetrico', consiste dei vettori che sono invarianti rispetto alle permutazioni, l'altro, detto ‛sottospazio antisimmetrico', consiste dei vettori che sono trasformati nei loro negativi da ogni trasposizione e quindi da ogni permutazione dispari. Si sostituisce il prodotto tensoriale rispetto a j dei prodotti tensoriali
ℋj1 ⊗ ℋj2 ... ⊗ ℋjnj,
con il prodotto tensoriale
ℋ01 ⊗ ℋ02 ...,
ove ℋ0j è il sottospazio antisimmetrico di ℋj1 ⊗ ℋj2 ... ⊗ ℋjnj, o il sottospazio simmetrico, a seconda che la particella del tipo in questione abbia spin 1/2, 3/2, 5/2, ... oppure spin 0, 1, 2, 3, ... Questa sostituzione ha l'effetto di ridurre notevolmente il numero dei possibili stati del sistema e la necessità di operare questa sostituzione fu scoperta cercando di spiegare perché atomi con due o più elettroni hanno un numero molto minore di linee spettrali di quante siano prevedibili nella teoria non modificata. Gli elettroni hanno spin 1/2 e il ben noto principio di esclusione di Pauli è una formulazione, in un certo senso vaga, delle conseguenze dell'uso del sottospazio antisimmetrico quando si abbia a che fare con più di un elettrone. Particelle come gli elettroni, per le quali si deve ricorrere al sottospazio antisimmetrico, si chiamano fermioni. Le altre prendono invece il nome di bosoni.
Avendo ridotto il problema di trovare il modello della meccanica quantistica per un sistema di particelle a quello di determinare le masse, gli spins e le mutue interazioni delle particelle, sorge ora il problema di vedere che cosa si può fare con questo modello. Una delle cose più importanti è la determinazione dello ‛stato di legame'. Non si tratta di stati nel senso definito precedentemente, ma di sottospazi dello spazio di Hilbert di tutti gli stati, i quali sono invarianti per traslazioni temporali e i cui elementi si comportano come gli stati di una singola particella libera. Fisicamente si pensa alle varie particelle del sistema come legate insieme in una singola particella composta, le cui parti mantengono fra loro relazioni fisse, ma che è libera di muoversi come un tutto unico. Per vedere se le particelle in un dato sistema possono essere così legate, si considera la rappresentazione proiettiva del gruppo di Galileo e si cerca di vedere se essa ha una sottorappresentazione irriducibile, vale a dire se la decomposizione integrale diretta in irriducibili ha componenti discrete. Ciascuna di queste corrisponde a un modo definito di legare le particelle fra loro ed è associata a un autovalore dell'hamiltoniano del sistema. Lo stato di legame il cui autovalore associato è il più piccolo si chiama ‛stato base' e gli altri si chiamano ‛stati eccitati'. È attraverso questo meccanismo che la meccanica quantistica spiega la formazione di atomi, molecole, cristalli nucleari e solidi a partire dai loro costituenti ‛elementari'. Un nucleo atomico è uno stato di legame di un numero finito di ‛protoni' e ‛neutroni'; un atomo è uno stato di legame di un nucleo atomico e di tanti elettroni quanti sono i protoni nel nucleo; una molecola è uno stato di legame di un certo numero di nuclei atomici e di tanti elettroni quanti sono i protoni dei nuclei costituenti. Da un punto di vista più fondamentale, atomi e molecole sono stati di legame di sistemi di protoni, neutroni ed elettroni, ma, studiandoli, può rivelarsi non solo possibile, ma anche conveniente, ignorare la struttura composita dei nuclei. Le interazioni tra elettroni e nuclei sono molto più semplici e meglio comprese che le interazioni tra protoni e neutroni e nello studio delle molecole si richiede soltanto una conoscenza superficiale dell'interazione fra nuclei. Un cristallo solido non è altro che una grossa molecola formata legando tra loro molte repliche di una molecola piccola. In questo modo, una volta note con sufficiente accuratezza le interazioni rilevanti, il problema di predire i possibili atomi e molecole e il tipo di interazione tra loro si riduce, almeno in linea di principio, a un problema di matematica pura.
La teoria delle rappresentazioni unitarie dei gruppi sostiene un ruolo importante non solo nella formulazione del problema della struttura degli atomi, molecole, nuclei, ecc., ma anche nella risoluzione di questi problemi. Prima di tutto, esiste un analogo nella meccanica quantistica del fatto classico secondo cui il centro di gravità di un sistema di particelle interagenti si muove indipendentemente dal movimento delle particelle intorno a questo centro di gravità. In base a questa analogia, la rappresentazione proiettiva del gruppo di Galileo G per un sistema di n particelle si fattorizza come la restrizione alla diagonale di G × G del prodotto tensoriale di due rappresentazioni proiettive di G. Una è irriducibile, ed è la rappresentazione irriducibile corrispondente a una particella priva di spin e di massa uguale alla somma delle masse delle particelle considerate. L'altra si riduce all'identità su un sottogruppo normale di G, il cui quoziente è il prodotto diretto R × T delle rotazioni e delle traslazioni temporali. Il primo fattore descrive il movimento del centro di gravità e il secondo il movimento relativo. Gli stati di legame corrispondono biunivocamente alle sottorappresentazioni discrete (di dimensione finita) della rappresentazione W di R × T. Equivalentemente essi corrispondono biunivocamente agli autovettori dell'operatore autoaggiunto H0, ove t ???14??? e-itH0 è la restrizione di W a e × T, e si devono contare due autovalori come uno solo quando essi stanno nello stesso sottospazio irriducibile di ℋ(W). In conclusione, il problema di trovare gli stati di legame si riduce essenzialmente a trovare lo spettro discreto di un certo operatore autoaggiunto H0 (di solito molto complicato). Questo problema viene affrontato nel modo seguente: si osserva che la rappresentazione W′, α ???14??? Wαe di R che commuta con H0 è la restrizione a R della rappresentazione unitaria U di un gruppo compatto K contenente R e che H0 si può scrivere nella forma H00 + J, ove H00 è nell'algebra commutante di U e J è una ‛piccola' perturbazione. H00 è tale che i suoi autovalori e autospazi possono essere determinati esplicitamente con metodi più o meno elementari. Naturalmente ogni autospazio definisce una sottorappresentazione di U che sarà sovente irriducibile e di solito di dimensione finita. I calcoli della ‛teoria delle perturbazioni del primo ordine' mostrano che, a meno che J sia abbastanza piccola, ciascun autovalore di H00 + J è approssimativamente la somma di un autovalore λ di H00 e di un autovalore dell'operatore ϕ ???14??? PλJ(ϕ) = Jλ(ϕ), ove Pλ è la proiezione su Mλ, l'autospazio di H00 corrispondente a λ, e ϕ è in Mλ. Se m1, m2, ..., mr sono gli autovalori di Jλ, si può pensare di avere ‛spezzato' λ, mediante la perturbazione J, in λ + m1, λ + m2, ..., λ + mr. Ora Mλ ha di solito una dimensione finita così alta che la ricerca degli autovalori di Jλ è un problema estremamente complicato in se stesso. Per afftontare questo problema si sfrutta il fatto che Jλ commuta con la restrizione di W′ a Mλ nel modo cui abbiamo precedentemente accennato. Quando le molteplicità con cui le rappresentazioni irriducibili di W′ compaiono in Mλ sono alte, questo artificio non è molto efficace, ma si può migliorare in questo modo: si approssima Jλ con un operatore Jλ′, il quale appartiene all'algebra commutante della restrizione di U a Mλ e di un sottogruppo chiuso K1 di K che contiene R, e si applica quindi la teoria della perturbazione del primo ordine per ottenere gli autovalori di Jλ a partire da quelli di Jλ′. Se si sceglie K1 in modo che la rappresentazione di K1 in Mλ sia priva di molteplicità, gli autovalori di Jλ′ possono essere calcolati esattamente, mentre le molteplicità che si hanno applicando la teoria dei gruppi per calcolare le connessioni saranno ridotte corrispondentemente. il procedimento può essere iterato e di fatto si cerca di ottenere una successione K ⊃ K1 ⊃ K2 ... ⊃ Kn ⊃ R di sottogruppi chiusi tali che la restrizione a Kj+1 di ciascuna rappresentazione irriducibile di Kj sia priva di molteplicità. Se si nesce a ottenere una tale successione, si ha di fatto un algoritmo che permette di avere un'approssimazione per ogni autovalore di H0 e uno schema di classificazione per questi autovalori che fa corrispondere a essi successioni finite π0, π1, ..., πn+1 di classi di equivalenza di rappresentazioni unitarie irriducibili di K = K0, di R = Kn e dei Kj. Questi schemi di classificazione per gli autovalori possono naturalmente applicarsi agli stati di legame del sistema e hanno notevole importanza quando si voglia ottenere una informazione qualitativa sui possibili nuclei, atomi e molecole e sulla spettroscopia' dei loro stati eccitati. Naturalmente nella maggior parte dei casi si ha un'~identita" tra alcune particelle del sistema e quindi intervengono svariati gruppi di permutazioni. Nel caso particolare di un atomo a n elettroni (rimandando a più tardi la riduzione antisimmetrica) il gruppo K sarà il prodotto diretto con se stesso del prodotto semidiretto (R × R ... × R) ???30??? Sn, ove si hanno n fattori in R × R ... × R, Sn è il gruppo delle permutazioni di n elementi e Sn opera in modo ovvio su R × R ... × R. Le rappresentazioni irriducibili di R × Sn × Sn sostengono un ruolo chiave nello schema di classificazione e la riduzione antisimmetrica elimina tutte quelle che non sono del tipo L × ???47??? × π, ove ???47??? è il prodotto di π con la rappresentazione non banale di dimensione 1 e π appartiene a una classe speciale di rappresentazioni irriducibili di Sn. Le particolari π che possono comparire sono parametrizzate in modo naturale da quegli interi non negativi v tali che n − v sia pari; un v siffatto risulta essere uguale alla ‛valenza chimica' del corrispondente stato eccitato dell'atomo. Se si calcola la valenza dello ‛stato di base' di un atomo a n elettroni, come funzione di n, si riscoprono le periodicità della tavola periodica degli elementi. Di fatto, la spiegazione offerta dalla meccanica quantistica del legame chimico mostra che si tratta di un fenomeno troppo complicato per poter essere descritto in modo abbastanza approssimato a partire da un concetto così semplice come quello di valenza.
Un nucleo, pur essendo uno stato di legame di due tipi di particelle, può essere trattato come uno stato di legame di particelle identiche facendo ricorso a un artificio che risale a Heisenberg e che ha acquistato notevole importanza in recenti ricerche sul comportamento di particelle elementari ad alta energia. Questo artificio consiste nel considerare la somma diretta ℋn ⊕ ℋp degli spazi di Hilbert degli stati del neutrone e del protone, rispettivamente, come spazio di Hilbert degli stati di una singola particella chiamata ‛nucleone' che può essere sia un protone che un neutrone. Naturalmente questo procedimento implica lo studio simultaneo di tutti i nuclei con lo stesso numero totale di particelle costituenti, indipendentemente dal modo in cui questo numero può essere scomposto in numero di protoni e di neutroni. Essi appaiono tutti come diversi stati di legame di n nucleoni identici interagenti. Questo artificio si dimostra particolarmente efficace perché il protone e il neutrone hanno press'a poco la stessa massa e inoltre reagiscono l'uno con l'altro in un modo che, da un certo punto di vista, è indipendente dal fatto che essi siano protoni o neutroni. La natura precisa di questa indipendenza può essere meglio spiegata dal punto di vista della teoria dei gruppi. Ritornando alla descrizione assiomatica di una particella mediante una rappresentazione proiettiva unitaria U del gruppo ℰ delle isometrie spaziali e un sistema di imprimitività P per U basato su S, vediamo cosa potrebbe accadere se ℰ fosse sostituito da ℰ × SU(2), ove SU(2) opera banalmente su S e ℰ si comporta come dianzi. In virtù delle stesse considerazioni precedenti, U risulterebbe indotto da una rappresentazione proiettiva unitaria di R × SU(2) e, se questa rappresentazione fosse irriducibile, e quindi del tipo L × M, U sarebbe UL×M ≃ UL × M. Se non si tenesse conto del fattore SU(2), si ‛vedrebbe' UL × M ristretto a ℰ; questa è la somma diretta di UL con se stesso un numero di volte uguale alla dimensione di M e si potrebbe pensare alla ‛particella' come a tante diverse particelle aventi lo stesso spin. Il nucleone può essere immaginato come una particella di questo tipo, con M = D1/2, la rappresentazione unitaria irriducibile di dimensione 2 di SU(2). In virtù della stretta relazione tra il modo in cui R e SU(2) intervengono nella teoria, s'introduce una nomenclatura parallela e si dice che il nucleo ha ‛spin isotopico' 1/2. Se si ignora la parte dell'interazione protone-protone dovuta alla carica elettrica positiva dei due protoni, si trova che l'interazione nucleone-nucleone è (almeno approssimativamente) invariante rispetto a ℰ × SU(2). Questa invarianza è il contenuto preciso dell'interazione neutrone-protone o indipendenza dalla ‛carica', che abbiamo ricordato precedentemente. Per il nucleone, L e M sono ambedue bidimensionali, così che L × M ha dimensione 4 e, pur non essendo una simmetria, SO(4) opera in modo naturale nello spazio di un nucleone e SO(4)n nello spazio di n nucleoni. Naturalmente opera anche SO(4)n ???30??? Sn e, come aveva segnalato Wigner nel suo lavoro del 1937, al quale abbiamo accennato dianzi, questa azione può essere utilizzata per classificare tutti i possibili nuclei nello spirito del procedimento generale descritto precedentemente.
Nel completare il procedimento che abbiamo succintamente indicato per classificare gli stati di legame per mezzo di successioni di sottogruppi chiusi e di loro rappresentazioni irriducibili, s'incontrano teoremi complicati della teoria delle rappresentazioni unitarie di gruppi, dei loro prodotti tensoriali e delle loro restrizioni a sottogruppi. Di conseguenza questo procedimento si sviluppò gradualmente, man mano che venivano scoperte tecniche più efficaci. Dopo le ricerche fondamentali di Wigner, tra il 1920 e il 1930, i contributi più importanti furono apportati da G. Racah, che rivoluzionò la trattazione gruppale dell'atomo a n elettroni in quattro lavori pubblicati tra il 1942 e il 1949. I metodi di Racah vennero poi adattati a problemi nucleari in una serie di lavori di H. A. John, H. van Wieringen e B. H. Flowers, pubblicati poco dopo il 1950.
Le applicazioni della teoria dei gruppi alla teoria dei cristalli hanno un carattere particolare dovuto al gran numero di particelle che intervengono. Di fatto, come accade sovente in situazioni di questo tipo, risulta utile passare al limite, considerando un cristallo infinito, in modo da poter utilizzare l'invarianza che ne risulta rispetto al gruppo discreto infinito Γ delle simmetrie del cristallo. Sarebbe troppo lungo e complicato esporre qui tutti i dettagli, ma vale la pena di segnalare che, per quanto riguarda gli effetti della Γ invarianza sulle così dette ‛bande' di energia, un passo importante risulta essere equivalente alla determinazione della struttura delle rappresentazioni UL del gruppo euclideo, indotte dalle varie rappresentazioni unitarie irriducibili L del sottogruppo Γ di ℰ.
Oltre al problema dello stato di legame per particelle interagenti, si ha il così detto ‛problema di scattering' (o problema di dispersione). Date due o più particelle che si muovono l'una nelle vicinanze dell'altra, in quale misura il cammino di una delle particelle libere è distorto dalla presenza delle altre? Qui ci s'interessa soprattutto a quella che potrebbe essere chiamata la forma asintotica del problema. Si suppone che le particelle siano all'inizio molto distanti l'una dall'altra, così da poter essere considerate essenzialmente libere, e si suppone che, dopo aver interagito, esse si separino nuovamente e divengano assimilabili a particelle libere col passare del tempo. Si vuole determinare lo ‛stato delle particelle libere' in un lontano futuro a partire da un passato remoto. Per analizzare questo problema, si confronta il gruppo dinamico attuale t ???14??? Vt = e-iHt con il gruppo dinamico che comparirebbe se non vi fosse interazione. Indicando quest'ultimo con V0t = e-iH0t, in molti casi si trova che, in accordo con il quadro fisico appena descritto, per molte traiettorie effettive t ???14??? Vt(ϕ) esistono, univocamente determinati, due vettori ϕ+ e ϕ- tali che
Si dice che l'interazione porta lo stato di particella libera ϕ- nello stato di particella libera ϕ+. Ogniqualvolta ϕ- e ϕ+ esistono, risulta chiaramente
Formula
onde si conclude facilmente che ϕ ???14??? ϕ- e ϕ ???14??? ϕ+ sono operatori lineari che conservano la norma. Indicando questi ultimi con S+ e S-, risulta: ϕ+ = S+(S-)-1(ϕ-1) e l'operatore S+ = (S-)-1 = S viene chiamato operatore di scattering (o di diffusione) o operatore S. Il suo rango e il suo dominio sono sottospazi invarianti per la rappresentazione t ???14??? V0t stabilisce un'equivalenza unitaria tra le sottorappresentazioni corrispondenti. Nell'importante caso particolare in cui il dominio e il rango costituiscono l'intero spazio di Hilbert, l'operatore Sè un elemento unitario dell'algebra commutante di V0. Esso commuta di fatto nello stesso modo con la rappresentazione soggiacente del gruppo delle simmetrie e - supponendo valida l'invarianza di Galileo - con la rappresentazione soggiacente del gruppo di Galileo. Ne segue, come di consueto, che S può essere parzialmente decomposto come somma diretta, sfruttando la decomposizione nota della rappresentazione in questione. Nell'importante caso particolare di due particelle (invarianti rispetto al gruppo di Galileo), questa decomposizione è particolarmente efficace, perchè le molteplicità con cui si presentano le componenti irriducibili nella decomposizione sono finite e uguali. Questo significa che S è completamente descritto da una funzione dalle classi di equivalenza delle rappresentazioni proiettive irriducibili alle matrici unitarie di un dato ordine finito. Le rappresentazioni che intervengono hanno una parametrizzazione canonica, ove i parametri sono determinati da un numero reale E e da un intero o da un semintero non negativo j. Pertanto S è completamente descritto da una funzione U di E e j avente per valori delle matrici unitarie. Quando ambedue le particelle hanno spin zero, le matrici hanno dimensione 1, cosicché U(E, j) è un numero complesso di modulo 1. Si scrive di solito U(E, j) = ei2δ(E,j), ove δ(E, j) è un numero reale che viene di norma chiamato ‛sfasamento'. Più in generale si può scrivere U(E, j) = ei2A(E,j), ove A(E, j) è una matrice autoaggiunta, e si ottiene così una matrice di ‛sfasamenti'. Questi elementi matriciali, come funzioni di E e j, sono strettamente legati a quanto abitualmente si osserva negli esperimenti di diffusione. Si può operare simultaneamente nei casi di urti neutrone-neutrone, neutrone-protone e protone-protone, utilizzando lo stesso artificio che rende possibile trattare un nucleo come uno stato di legame di particelle identiche. Si considera la diffusione nucleone-nucleone, dove il nucleone è la combinazione protone-neutrone descritta precedentemente ed è visto come avente spin isotopico 1/2 e invariante rispetto all'azione di ℰ × SU(2). Lo spin isotopico è trattato più o meno come lo spin ordinario e fa crescere la dimensione delle matrici U(E, j). D'altra parte l'invarianza rispetto a SU(2) indica delle relazioni tra gli sfasamenti per differenti accoppiamenti, che sono confermate dall'esperienza.
Di fatto, esperimenti sugli urti tra neutrone e protone sono condotti a energie così alte che le leggi invarianti per il gruppo di Galileo non sono un'approssimazione abbastanza buona e sfortunatamente non è stato ancora possibile trovare leggi invarianti rispetto al gruppo di Lorentz (Poincaré) che si accordino con i dati sperimentali e che siano matematicamente ben definite. D'altra parte, ricorrendo a considerazioni più elaborate, si possono modificare gli sviluppi indicati precedentemente, in modo da supporre soltanto l'invarianza rispetto a isometrie spaziali, arrivando ancora alla conclusione che la diffusione è descritta da una funzione di E e j a valori nelle matrici unitarie. Inoltre, le considerazioni relative allo spin isotopico (al pari degli effetti di ogni accrescimento di ℰ del tipo ℰ × K) possono essere incluse in questa nuova impostazione senza alcun cambiamento essenziale. La nozione di spin isotopico crebbe d'importanza con la scoperta, nel 1947, di nuove particelle le cui interazioni tra loro e con i nucleoni potevano essere meglio comprese raggruppandole secondo multipletti di spin isotopico come il protone e il neutrone. Mentre non esisteva (e tuttora non esiste) una teoria che permettesse di calcolare gli elementi matriciali di U(E, j) a partire da un'interazione nota, si potevano osservare svariate relazioni tra di essi e dimostrare che si avevano di fatto delle conseguenze dell'invarianza rispetto a SU(2) abbinata all'appropriato raggruppamento in multipletti. Queste nuove particelle venivano ‛create' quando interagivano nucleoni ad alta energia e la teoria dell'operatore S dovette naturalmente essere modificata per inquadrare tale interazione e la successiva ‛annichilazione'.
Le prime nuove particelle che vennero inquadrate in questo schema furono i mesoni π la cui esistenza era stata prevista da Yukawa già nel 1935. Si trattava di tre particelle, tutte di spin 0, indicate con π+, π0 e π- a seconda della loro carica elettrica. L'ipotesi che esse formassero un tripletto di spin isotopico 1 era in accordo con i fatti sperimentali. Quando vennero scoperte altre particelle, alcune di spin 1/2 e altre di spin 0, si suppose che le particelle di spin isotopico 1/2 fossero raggruppate in doppietti di spin isotopico 1/2 e che le particelle di spin 0, come i mesoni π, fossero raggruppate in tripletti di spin isotopico 1, anche se l'esistenza di alcune delle particelle necessarie a completare questo quadro non era ancora stata stabilita. Tuttavia non fu facile spiegare molte proprietà qualitative dell'interazione fino a che, nel 1953, M. Gell-Mann e Nishijima scoprirono indipendentemente che si potevano spiegare queste anomalie raggruppando tutte le sei particelle nei tre doppietti isotopici, un singoletto, un doppietto e un tripletto, facendo aggiustamenti simili per le particelle di spin 0. Questa sorprendente applicazione della teoria dei gruppi alla teoria delle interazioni fra particelle era soltanto agli inizi. Nel 1957 Gell-Mann e Schwinger introdussero indipendentemente un concetto di ‛simmetria globale' collegando le proprietà di diffusione delle nuove particelle in diversi multipletti isotopici. In seguito a ciò Gell-Mann e Ne'eman, nel 1961, estesero notevolmente il concetto di spin isotopico. Ritornando all'impostazione per cui ℰ deve essere sostituito da ℰ × SU(2), per quanto concerne l'assiomatica di una particella, supponiamo che SU(2) sia rimpiazzato da SU(3). Una particella sarà associata a una rappresentazione proiettiva irriducibile di R × SU(3). Per le particelle di spin 1/2 questa sarà D1/2 × M, per un'opportuna rappresentazione unitaria irriducibile M di SU(3). D'altra parte, dal punto di vista di chi conosca soltanto SU(2), questa ‛particella' non sarà che la sovrapposizione di tanti multipletti di spin isotopico quante sono le componenti irriducibili della restrizione di M a SU(2). Ora, SU(3) ha una rappresentazione irriducibile di dimensione 8, la cui restrizione a SU(2) è equivalente a D1/2 ⊗ D1/2 ⊗ D0 ⊗ D1. In questo modo il nucleone e i nuovi multipletti di spin 1/2, ai quali abbiamo dianzi accennato, possono essere tutti sistemati in un ‛supermultipletto' SU(3). Le particelle di spin 0 possono essere trattate in modo analogo e similmente possono essere trattate un gran numero di particelle che vennero scoperte più tardi. Inoltre molte delle relazioni che possono essere previste in base all'invarianza rispetto a SU(3) furono riconosciute, almeno approssimativamente, valide. Sulla scia di questi successi, venne proposto un altissimo numero di altri schemi di simmetria, che vennero sperimentati con vario successo. Uno, che fu la base di molti lavori successivi, fu lo schema SU(6) introdotto nel 1964 da Sakita e indipendentemente da Radicati e Gursey. Il loro SU(6) mescola spin e SU(3) in modo simile a quello secondo cui l'SU(4) di Wigner mescola lo spin con SU(2). Esso ha ottenuto notevoli successi, ma ha anche incontrato serie difficoltà concettuali. Da allora le ricerche si sono talmente ampliate che è impossibile darne una descrizione concisa. Basti dire che, con la speranza di trovare schemi in grado di spiegare tutte le particelle scoperte o da scoprire, i fisici sono stati indotti a compiere ricerche di ampio respiro nel campo della teoria delle rappresentazioni unitarie dei gruppi di Lie semisemplici ‛non compatti'.
17. Considerazioni generali.
Scopo di questo articolo è stato sia spiegare la natura generale della teoria dei gruppi e i suoi principali concetti sia indicare l'applicabilità piuttosto estesa dei metodi e dei punti di vista della teoria dei gruppi ad altri rami della matematica e della fisica. Il campo di applicazione è così vasto che è difficile distinguere tra un resoconto ragionevolmente ampio e un articolo che si occupi di tutta la matematica e tutta la fisica. Il compromesso che abbiamo adottato è stato di scegliere alcuni dei campi di applicazione più importanti e di descrivere in modo sufficientemente dettagliato questi campi e i loro legami con la teoria dei gruppi. È stato naturalmente necessario scendere poi ad altri compromessi, poiché ciascuno dei campi scelti è talmente vasto, anche considerando soltanto i suoi aspetti legati alla teoria dei gruppi, da non poter essere comprensibilmente riassunto nello spazio che avevamo a disposizione. Le scelte fatte rispecchiano sia i limiti dell'autore sia la sua personale opinione su ciò che è più o meno fondamentale e su ciò che semplicemente è troppo difficile da spiegare.
Se avessimo avuto a disposizione più tempo e più spazio, avremmo aggiunto un capitolo su teoria dei gruppi e geometria algebrica e un altro su teoria dei gruppi e calcolo delle probabilità. Naturalmente il primo avrebbe avuto necessariamente stretti legami con il cap. 15 e avrebbe potuto forse addirittura fondersi con tale capitolo. Avrebbe potuto includere una descrizione di certe ulteriori applicazioni della teoria dei gruppi alla teoria dei numeri, coinvolgendo la teoria dei punti razionali e interi sulle varietà algebriche. Le proprietà di teoria dei numeri delle cosiddette ‛curve ellittiche' sono state studiate in modo sistematico facendo spesso ricorso alla teoria dei gruppi. Vi sono gruppi algebrici più generali dei gruppi algebrici lineari descritti nel cap. 9, ma ciascuno di essi contiene un sottogruppo normale commutativo con un quoziente lineare. I gruppi algebrici commutativi che non sono lineari vengono chiamati varietà abeliane e sono generalizzazioni delle varietà abeliane descritte nel cap. 15. La teoria di queste varietà è un ramo della geometria algebrica notevolmente sviluppato del quale deve tener conto ogni esposizione di teoria dei gruppi e geometria algebrica. Una tale esposizione dovrebbe anche occuparsi degli importanti legami esistenti tra la teoria dei gruppi e la teoria classica degli invarianti, come ha spiegato Weyl nel suo libro The classical groups e come ha chiarito ulteriormente Mumford nel suo recente libro Geometric invariant theory.
Il capitolo su teoria dei gruppi e calcolo delle probabilità avrebbe dato maggiore enfasi al ruolo della nozione di transitività metrica o ergodicità (v. sopra, cap. 11) nel rendere possibile un modello matematico che ponga in evidenza l'andamento ‛casuale' nonché al ruolo centrale sostenuto dal teorema ergodico nei confronti della teoria dei ‛processi stocastici stazionari'. Molti altri argomenti avrebbero dovuto essere approfonditi; in particolare il ruolo chiave sostenuto dall'analisi di Fourier sia nella sua forma classica che nell'ambito della teoria delle rappresentazioni. La discussione del ruolo dell'ergodicità nella meccanica statistica e l'uso sistematico della teoria dei gruppi in certi problemi risolubili nella teoria delle ‛transizioni di fase' avrebbe messo in evidenza i rapporti tra questi argomenti e il contenuto del cap. 16.
Naturalmente molti altri capitoli avrebbero potuto ragionevolmente essere dedicati alle applicazioni: per esempio le applicazioni alla geometria differenziale. Limiti di spazio e di tempo ci hanno costretto a omettere molti aspetti importanti della pura teoria dei gruppi. I pochi accenni ai gruppi discreti infiniti nel cap. 15 non danno certamente un resoconto fedele di un argomento studiato in modo esteso. Non abbiamo neppure accennato, per esempio, al famoso problema di Burnside e ai suoi legami con la logica, né agli elaborati teoremi di struttura che sono stati stabiliti per i gruppi commutativi numerabili. Altri argomenti che non abbiamo incluso sono la teoria dei semigruppi, la teoria delle rappresentazioni integrali dei gruppi, la teoria delle categorie di gruppi e i gruppi e le algebre di Lie a infinite dimensioni. L'elenco è lungi dall'essere completo. Bisogna anche tenere presente che l'argomento centrale dell'analisi armonica è ben lontano dal- l'essere esaurito dalla teoria degli oggetti a quadrato sommabile, dei quali ci siamo quasi esclusivamente occupati in questo articolo.
Bibliografia.
Abel, N. H., Mémoire sur les équations algébriques, ou l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré, Christiania 1824; in Oeuvres complètes (a cura di M. M. L. Sylow et S. Lie), vol. I, Christiania 1881, pp. 28-33.
Abel, N. H., Recherches sur les fonctions elliptiques, in ‟Journal Crelle", 1927, II.
Auslander, L., Kostant, B., Quantization and representations of solvable Lie groups, in ‟Bulletin of the American Mathematical Society", 1967, LXXIII, pp. 692-695.
Baer, R., Group elements of prime power index, in ‟Transactions of the American Mathematical Society", 1953, LXXV, pp. 20-47.
Baer, R., Nilpotent characteristic subgroups of finite groups, in ‟American journal of mathematics", 1953, LXXV, pp. 633-644.
Bargmann, V., Irreducible unitary representations of the Lorentz groups, in ‟Annals of mathematics", 1947, XLVIII, pp. 568-640.
Borel, A., Groupes linéaires algébriques, in ‟Annals of mathematics", 1956, LXIV, pp. 20-80.
Borel, A., Harish-Chandra, Arithmetic subgroups of algebraic groups, in ‟Annals of mathematics", 1962, LXXV, pp. 485-535.
Brauer, R., Applications of induced characters, in ‟American journal of mathematics", 1947, LXIX, pp. 709-716.
Brauer, R., Nesbitt, C., On modular characters of groups, in ‟Annals of mathematics", 1941, XLII, pp. 556-590.
Bruhat, F., Distributions sur un groupe localement compact et applications à l'étude des représentations des groupes p-adiques, in ‟Bulletin de la Société Mathématique de France", 1961, LXXXIX, pp. 43-75.
Bruhat, F., Sur les représentations des groupes classiques p-adiques. I, in ‟American journal of mathematics", 1961, LXXXIII, pp. 321-338.
Bruhat, F., Sur les représentations des groupes classiques p-adiques. II, in ‟American journal of mathematics", 1961, LXXXIII, pp. 343-368.
Burnside, W., Theory of groups of finite order, London 1897, 19112.
Cartan, É., Sur la structure des groupes simples finis et continus, in ‟Compte rendu hebdomadaire des séances de l'Académie de France", 1893, CXVI.
Cauchy, A.-L., Sur la détermination du nombre des racines dans les équations algébriques, in ‟Journal de l'École polytechnique", 1815, X, pp. 457-548.
Cayley, A., On the theory of groups, a depending on the symbolic equation Ψn = 1, in ‟Philosophical magazine", 1954, VII.
Chevalley, C., Théorie des groupes de Lie, vol. II, Paris 1951, vol. III, Paris 1955.
Chevalley, C., Sur certains groupes simples, in ‟Tohoku mathematical journal", 1955, VII, pp. 14-66.
Dedekind, R., Sur la théorie des nombres entiers algébriques, in ‟Bulletin des sciences mathématiques de Darboux", 1876, XI, pp. 278-288.
Dickson, L. E., Linear groups with an exposition of the Galois field theory, Leipzig 1921.
Dieudonné, J. A., Sur les groupes classiques, Paris 1948.
Dirichlet (Lejeune), P. G., Vorlesungen über Zahlentheorie, Braunschweig 1963.
Eichler, M., Quadratische Formen und orthogonale Gruppen, Berlin-Gottingen-Heidelberg 1952.
Eisenstein, F. G., Beiträge zur Theorie der elliptischen Functionen. III. Fernere Bemerkungen zu den Transformationsformeln, in ‟Journal Crelle", 1846, XXXII, pp. 59-70.
Eisenstein, F. G., Beiträge zur Theorie der elliptischen Functionen. VI. Genaue Untersuchung der unendlichen Doppelproducte, aus welchen die elliptischen Functionen als Quotienten zusammengesetzt sind, und der mit ihen zusammenhängenden Doppelreihen, in ‟Journal Crelle", 1847, XXXV, pp. 153-274.
Feit, W., Characters of finite groups, New York 1967.
Feit, W., The current situation in the theory of finite simple groups, in ‟Proceedings of the International Congress of Mathematicians", 1970, I, pp. 55-93.
Feit, W., Thompson, J. G., Solvability of groups of odd order, in ‟Pacific journal of mathematics", 1963, XIII, pp. 755-1029.
Frobenius, G., Über Gruppencharaktere, in ‟Monatsberichte der Berliner Akademie", 1870, pp. 985-1021.
Furstenberg, H., A Poisson formula for semi-simple Lie groups, in ‟Annals of mathematics", 1963, LXXVII, pp. 335-386.
Galois, É., Mémoire sur les conditions de résolubilité des équations par radicaux (1831), in Oeuvres mathématiques d'Évariste Galois, Paris 1897.
Gauss, C. F., Disquisitiones aritmeticae, Lipsia 1801.
Gelfand, I. M., The center of an infinitesimal group ring, in ‟Matematischeskij j sbornik" (nuova serie), 1950, XXVI, pp. 103-112.
Gelfand, I. M., Fomin, S. V., Geodesic flows on manifolds of constant negative curvature, in ‟Uspekhi matematicheskikh nauk", 1952, VII, pp. 118-137.
Gelfand, I. M., Graev, M. I., Representations of the group of second order matrices with elements in a locally compact field and special functions on locally compact fields, in ‟Uspekhi matematicheskikh nauk", 1963, XVIII, pp. 29-99.
Gelfand, I. M., Naimark, M. A., Unitary representations of the classical groups, in ‟Trudy Matematicheskogo Instituta imeni V. A. Steklova", 1950, XXXVI, p. 288.
Gelfand, I. M., Pjatetskij-Shapiro, I., Automorphic functions and the theory of representations, in ‟Trudy Moskovskogo matematischeskogo obshchestva", 1963, XII, pp. 389-412.
Gleason, A., Groups without small subgroups, in ‟Annals of mathematics", 1952, LVI, pp. 193-212.
Gorenstein, D., Finite groups, New York-Evanston-London, 1968.
Green, J. A., The characters of the finite general linear groups, in ‟Transactions of the American Mathematical Society", 1955, LXXX, pp. 402-447.
Haar, A., Der Massbegriff in der Theorie der kontinuierlichen Gruppen, in ‟Annals of mathematics", 1933, XXXIV, pp. 147-169.
Hall, P., On the Sylow system of a soluble group, in ‟Proceedings of the London Mathematical Society", 1937, XLIII, pp. 316-323.
Harish-Chandra, Representations of semi-simple Lie groups. II, in ‟Transactions of the American Mathematical Society", 1954, LXXVI, pp. 26-65.
Harish-Chandra, Representations of semi-simple Lie groups. III, in ‟Transactions of the American Mathematical Society", 1954, LXXVI, pp. 234-253.
Harish-Chandra, Spherical functions on a semi-simple Lie group. I, in ‟American journal of mathematics", 1958, LXXX, pp. 241-310.
Harish-Chandra, Spherical functions on a semi-simple Lie group. II, in ‟American journal of mathematics", 1958, LXXX, pp. 553-613.
Harish-Chandra, Invariant eigendistributions on semi-simple Lie groups, in ‟Bulletin of the American Mathematical Society", 1963, LXIX, pp. 117-123.
Harish-Chandra, Automorphic forms on semi-simple Lie groups, Lecture notes in mathematics No 62, Berlin-Heidelberg-New York 1968.
Hermite, Ch., Sur les fonctions algébriques, in ‟Compte rendu hebdomadaire des séances de l'Académie de France", 1851, XXXII, pp. 458-461.
Hochschild, G., Serre, J.-P., Cohomology of group extensions, in ‟Transactions of the American Mathematical Society", 1953, LXXIV, pp. 110-134.
Iwasawa, K., On some types of topological groups, in ‟Annals of mathematics", 1949, L, pp. 507-558.
Jacobi, C. G. J., Fundamenta nova theoriae functionum ellipticarum, Königsberg 1829.
Jacquet, H., Langlands, R. P., Automorphic forms on GL(2), Lecture notes in Mathematics, No 114, Berlin-Heidelberg-New York 1970.
Jordan, C., Traité des substitutions et des équations algébriques (1870), Paris 1870.
Kirillov, A. A., Infinite dimentional unitary representations of a second order matrix group with elements in a locally compact field, in ‟Doklady Kademii Nauk SSSR", 1963, CL, pp. 740-743.
Klein, F., Vergleichende Betrachtungen über neuere geometrische Forschungen, in ‟Mathematische Annalen", 1893, XLIII.
Kronecker, L., Auseinandersetzung einiger Eigenschaften der Klassenanzahl idealer, complexer Zahlen, in ‟Monatsberichte der Berliner Akademie", 1870, pp. 1021-1035.
Kummer, E. E., Bestimmung der nzahl nicht äquivalenter Classen für die aus λ teu Wurzeln der Einheit gebildeten complexen Zahlen und die idealen Factoren derselben, in ‟Journal Crelle", 1850, XL, pp. 93-116.
Kummer, E. E., Über eine Eigenschaft der Einheiten der aus den Wurzeln der Gleichung αλ = I gebildeten complexen Zahlen und über den zweiten Faktor der Klassenzahl, in ‟Monatsberichte der Berliner Akademie", 1870, pp. 855-880.
Lagrange, J.-L., Réflexions sur la résolution algébrique des équations, in Oeuvres de Lagrange (a cura di J. A. Serret), vol. III, Paris 1879, pp. 203-421.
Legendre, A.-M., Essai sur la théorie des nombres, Paris 1798.
Lie, S., Engel, F., Theorie der Transformations Gruppe, vol. III, Leipzig 1893.
Lyndon, R. C., The cohomology theory of group extensions, in ‟Duke mathematical journal", 1948, XV, pp. 271-292.
Mackey, G. W., On a theorem of Stone and von Neumann, in ‟Duke mathematical journal", 1949, XVI, pp. 226-313.
Mathieu, E., Mémoire sur l'étude des fonctions de plusieurs quantités, sur la manière de les former et sur les substitutions qui les laissent invariables, in ‟Journal mathématique de Lionville" (II série), 1861, VI, pp. 241-323.
Mathieu, E., Sur la fonction cinq fois transitive de 24 quantités, in ‟Journal mathématique de Lionville", (II série), 1873, XVIII, pp. 25-46.
Mautner, F. I., Spherical functions over p-adic fields, in ‟American journal of mathematics", 1958, LXXX, p. 441-457.
Montgomery, D., Zippin, L., Topological transformation groups, New York 1955.
Moore, C. C., Compactifications of symmetric spaces. I, in ‟American journal of mathematics", 1964, LXXXVI, pp. 201-218.
Moore, C. C., Compactifications of symmetric spaces. II. The Cartan domain, in ‟American journal of mathematics", 1964, LXXXVI, pp. 358-378.
Moore, C. C., Extensions and low dimensional cohomology of locally compact groups. I and II, in ‟Transactions of the American Mathematical Society", 1964, CXIII, pp. 40-86.
Murray, F. J., Neumann, J. von, On rings of operators, in ‟Annals of mathematics", 1936, XXXVII, pp. 116-229.
Netto, E., Substitutions Theorie und ihre Anwendung auf die Algebra, Leipzig 1882.
Neumann, J. von, The uniqueness of Haar's measure, in ‟Matematischeski sbornik" (N. S. 1), 1934, pp. 106-114.
Ono, T., Sur une propriété arithmétique des groupes commutatifs, in ‟Bulletin de la Société Mathématique de France", 1957, LXXXV, pp. 307-323.
Paley, R., Wiener, N., Fourier transforms in the complex domain, New York 1934.
Pukanzsky, L., On the characters and the Plancherel formula of nilpotent groups, in ‟Journal of functional analysis", 1967, pp. 255-280.
Pukanzsky, L., On the theory of exponential groups, in ‟Transactions of the American Mathematical Society", 1967, CXXVI, pp. 487-507.
Pukanszky, L., On the unitary representations of exponential groups, in ‟Journal of functional analysis", 1968, pp. 73-113.
Ruffini, P., Riflessioni intorno alla soluzione delle equazioni algebriche generali, Modena 1813; in Opere matematiche (a cura di E. Bortolotti), vol. II, Roma 1953, pp. 155-268.
Sally, P. J., Shalika, J. A., Characters of the discrete series of representations of SL(2) over a local field, in ‟Proceedings of the National Academy of Sciences", 1968, LXI, pp. 1131-1137.
Sally, P. J., Shalika, J. A., The Plancherel formula for SL(2) over a local field, in ‟Proceedings of the National Academy of Sciences", 1969, LXIII, pp. 661-667.
Satake, I., Theory of spherical functions on reductive algebraic groups over p-adic fields, Publ. I.H.E.S. No 18, 1963, pp. 5-69.
Schreier, O., Abstrakte kontinuierliche Gruppen, in ‟Abhandlungen aus dem mathematischen Seminar, Universität Hamburg", 1926, IV, pp. 15-32.
Selberg, A., Harmonic analysis and discontinuous groups in weakly summetric Riemannian spaces with applications to Dirichlet series, in ‟Journal of the Indian Mathematical Society", 1956, XX, pp. 47-87.
Serret, J. A., Cours d'algèbre supérieure, 2 voll., Paris 18663.
Steenrod, N., The topology of fiber bundles, Princeton 1951.
Steinberg, R., The simplicity of certain groups, in ‟Pacific journal of mathematics", 1960, X, pp. 1039-1041.
Stone, M. H., Linear transformations in Hilbert space and their applications to analysis, New York 1932.
Suzuki, M., The non-existence of a certain type of simple groups of odd order, in ‟Proceedings of the American Mathematical Society", 1957, VIII, pp. 686-(%5.
Suzuki, M., A new type of simple groups of finite order, in ‟Proceedings of the National Academy of Sciences", 1960, XLVI, pp. 868-870.
Sylow, L., Théorèmes sur les groupes des subtitutions, in ‟Mathematische Annalen", 1872, V, pp. 584-594.
Tanaka, S., On irreducible unitary representations of some special linear groups of the second order. I, in ‟Osaka journal of mathematics", 1966, III, pp. 217-227.
Tanaka, S., On irreducible unitary representations of some special linear groups of the second order. II, in ‟Osaka Journal of mathematics", 1966, III, pp. 229-242.
Thompson, J. G., A special class of non solvable groups, in ‟Mathematische Zeitschrift", 1960, LXXII, pp. 458-462.
Thompson, J. G., Non solvable finite groups all of whose local subgroups are solvable, in ‟Pacific journal of mathematics", 1968.
Tits, J., Les groupes simples de Suzuki et de Ree, Sém. Bourbaki, décembre 1960.
Tits, J., Théorème de Bruhat et sousgroupes paraboliques, in ‟Compte rendu hebdomadaire des séances de l'Académie des Sciences", 1962, CCLIV, pp. 2910-2912.
Weber, H., Lehrbuch der Algebra, 2 voll., Braunschweig 1895-1896.
Weil, A., Sur les groupes topologiques et les groupes measurés, in ‟Compte rendu hebdomadaire des séances de l'Académie des Sciences", 1936, CCII, pp. 1147-1149.
Weil, A., L'intégration dans les groupes topologiques et ses applications, Paris 1940.
Weil, A., Sur certains groupes d'opérateurs unitaires, in ‟Acta mathematica", 1964, CXI, pp. 143-211.
Weil, A., La formule de Siegel et les groupes classiques, in ‟Acta mathematica", 1965, CXIII, pp. 187.
Weyl, H., Gruppentheorie und Quantenmechanik, Leipzig 19312.
Weyl, H., The classical groups, Princeton 19462.
Wightman, A. S., On the localizability of quantum mechanical systems, in ‟Review of modern physics", 1962, XXXIV, pp. 845-872.
Wigner, E. P., On unitary representations of the inhomogeneous Lorentz group, in ‟Annals of mathematics", 1939, XL, pp. 149-204.
Wigner, E. P., Group theory and its applications to quantum mechanics of atomic spectra, New York-London 1959.
Wigner, E. P., Newton, T. D., Localized states for elementary systems, in ‟Review of modern physics", 1949, XXI, pp. 400-406.