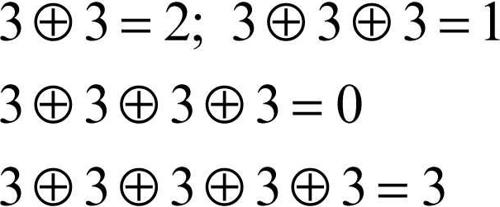gruppo ciclico
gruppo ciclico
gruppo ciclico gruppo in cui ogni elemento può essere ottenuto come potenza di un suo elemento g, detto generatore del gruppo. Un gruppo ciclico è abeliano e ogni suo sottogruppo è ciclico; dato un elemento g ∈ G, il minimo intero n, se esiste, per il quale gn è uguale all’elemento neutro del gruppo è detto ordine di g; se tale numero non esiste g ha ordine infinito. Se G è un gruppo finito di ordine n e se p è un numero primo che divide n, allora esiste in G un elemento di ordine p (teorema di Cauchy). Da ciò segue che ogni gruppo finito il cui ordine sia un numero primo è necessariamente ciclico.
Un gruppo ciclico infinito è isomorfo al gruppo Zn(+) dei numeri interi con l’operazione di addizione e 1 ne è il generatore. Un gruppo ciclico finito di ordine n è isomorfo al gruppo Zn delle classi resto modulo n e ogni suo elemento m coprimo con n può essere un suo generatore; per esempio in Z4 = {0, 1, 2, 3} con l’operazione ⊕ di addizione ciclica, l’elemento 3 è un generatore perché addizionato a sé stesso più volte ne fornisce tutti gli elementi:
