isometrie, gruppo delle

isometrie, gruppo delle

isometrie, gruppo delle struttura algebrica di gruppo che si ottiene definendo nell’insieme I delle isometrie (del piano e dello spazio) l’operazione di composizione di trasformazioni (→ funzioni, composizione di). Per ogni coppia ƒ e g di isometrie elementi di I, la trasformazione prodotto ƒ ∘ g è la trasformazione che si ottiene operando prima con g e poi con ƒ. Infatti, il corrispondente (→ immagine) di un punto P è il punto P′ dato da ƒ ∘ g(P) = ƒ(g(P)). Rispetto all’operazione così definita, l’insieme I delle isometrie assume la struttura di gruppo. Le traslazioni, così come le rotazioni di dato centro, formano un sottogruppo abeliano (cioè commutativo).

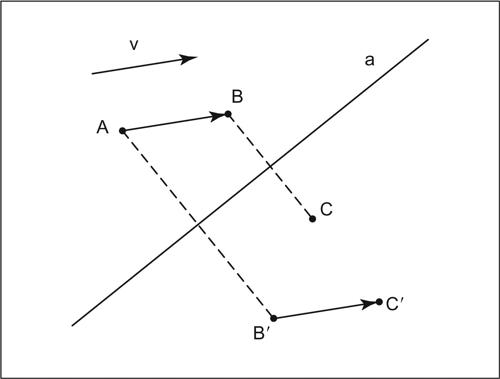
Il gruppo delle isometrie è un gruppo non commutativo. Si osserva infatti, per esempio, che componendo nel piano una traslazione con una simmetria assiale il risultato della trasformazione composta dipende dall’ordine in cui traslazione e simmetria sono eseguite. Nella figura, il corrispondente di A nella trasformazione composta è C o C′ a seconda che si esegua prima la traslazione di vettore v e poi la simmetria assiale di asse a, o viceversa.