Klein, gruppo di
Klein, gruppo di
Klein, gruppo di in algebra, gruppo commutativo di ordine 4, solitamente indicato con la lettera V (dal tedesco Vier, cioè quattro), definito come il gruppo delle isometrie del piano che fissano un rettangolo che non sia un quadrato: tali isometrie sono quella identica (1), le simmetrie a e b rispetto ai due assi di simmetria del rettangolo e la rotazione c di ampiezza π radianti (vale a dire 180°) attorno al suo centro. Come gruppo, il gruppo di Klein è generato dalle due simmetrie a e b, rispetto alle quali ammette la presentazione
che lo rende isomorfo al gruppo diedrale D2.
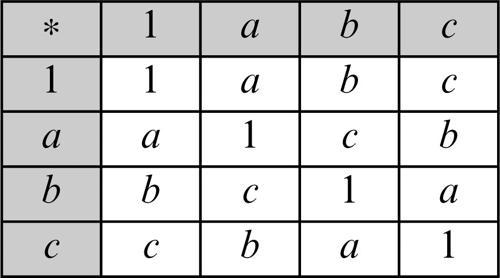
L’operazione ∗ che determina la struttura di gruppo su V è definita dalla seguente tabella di → Cayley:
dove, nella cella in cui si incrociano la riga relativa a un elemento g (posto sulla prima colonna) e la colonna relativa a un elemento h (posto sulla prima riga), è indicato il prodotto g ∗ h. Il gruppo di Klein è anche riportato in letteratura come gruppo trirettangolo (o delle tre simmetrie, poiché la rotazione di ampiezza π attorno al centro del rettangolo coincide con la simmetria rispetto a tale punto) e come gruppo quadrinomio, essendo formato da quattro elementi; la notazione tedesca di Viergruppe è spesso ripresa anche in testi italiani.