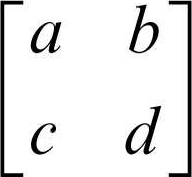gruppo modulare

Enciclopedia della Matematica (2013)

gruppo modulare


gruppo modulare gruppo di trasformazioni lineari fratte z del semipiano superiore H dei numeri complessi del tipo a + ib con b > 0 (semipiano superiore del piano di Argand-Gauss) aventi la forma z → (az + b)l (cz + d) dove a, b, c, d sono interi, ad − bc = 1 e l’operazione del gruppo è la composizione di funzioni. Il gruppo è isomorfo al gruppo delle matrici M2(Z) a elementi interi

formula

dove a, b, c e d sono interi, il determinante è 1 e coppie di matrici M e −M sono considerate come identiche; l’operazione è in questo caso il prodotto righe per colonne tra matrici.

Vedi anche
isomorfismo In matematica, corrispondenza biunivoca tra due insiemi dotati di ‘strutture’, la quale conservi le strutture stesse. Le strutture sono di tre tipi: d’ordine, algebriche e topologiche, e si hanno perciò tre diversi tipi di isomorfismi. I. tra insiemi dotati di strutture d’ordine (i. d’ordine) Si tratta ... gruppo simplettico In matematica, il gruppo costituito dalle matrici s. di ordine 2n (simbolo Sp2n). Una matrice A di ordine 2n si chiama s. se risulta A*J=JA–1, ove J è la matrice di ordine 2n formata da n blocchi (01 –10) situati lungo la diagonale principale e A*, A–1 sono rispettivamente le matrici trasposta e inversa ... numeri interi In matematica, si chiamano interi positivi (o naturali) i numeri della successione infinita 1, 2, 3, 4, ... ciascuno dei quali si ottiene dal precedente aggiungendo a esso l’unità. Gli interi negativi sono numeri della successione −1, −2, −3, ... Gli interi positivi e negativi, insieme con lo zero, si ... congruenza Nella geometria elementare, sinonimo di uguaglianza (➔) diretta, cioè di sovrapponibilità. Nella teoria dei numeri, relazione di due numeri interi relativi a, b tali che la differenza a−b è divisibile per un numero intero positivo m (detto modulo di una c.); essa si scrive a≡b (mod. m) e si legge: «a ...
Tag
Vocabolario
modulare¹
modulare1 modulare1 agg. [der. di modulo]. – Relativo a un modulo (nel suo sign. primo e più generale), basato su un modulo, e quindi anche costituito dal vario accostamento di elementi (detti essi stessi elementi m.) che ripetono le misure,...
modulare²
modulare2 modulare2 v. tr. [dal lat. modulari o modulare, der. di modŭlus: v. modulo] (io mòdulo, ecc.). – 1. In musica: a. Far passare la voce o i suoni da una tonalità a un’altra. b. Regolare l’intensità e il timbro della voce nel canto,...