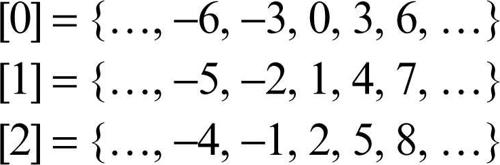gruppo

gruppo

gruppo struttura algebrica con una operazione, alla base della definizione di molte altre strutture, quali gli anelli, i campi, gli spazi vettoriali ecc. È un insieme non vuoto G dotato di una operazione binaria ∗: G × G → G che gode della proprietà associativa e tale che esiste l’elemento neutro e ogni elemento ammette l’inverso. Formalmente, un gruppo è quindi una coppia (G, ∗), dove G è un insieme e ∗ è un’operazione binaria su G, che associa a ogni coppia di elementi a e b di G un terzo elemento di G denotato con a ∗ b, che soddisfa i seguenti assiomi:

• ∀a, b, c ∈ G, (a ∗ b) ∗ c = a ∗ (b ∗ c)

(associatività)

• ∃e ∈ G: ∀a ∈ G, a ∗ e = e ∗ a = a

(esistenza dell’elemento neutro)

• ∀a ∈ G, ∃i (a) ∈ G: i (a) ∗ a = a ∗ i (a) = e

(esistenza dell’inverso)

Un gruppo G con operazione ∗ è anche indicato con G(∗). L’elemento neutro e è in effetti unico; similmente, per ogni elemento a di G, è unico il suo inverso i (a). Un gruppo G si dice commutativo (o abeliano) se l’operazione ∗ è commutativa, ossia se è soddisfatto l’ulteriore assioma

• ∀a, b ∈ G, a ∗ b = b ∗ a

(proprietà commutativa)

L’insieme Z dei numeri interi è un gruppo commutativo rispetto all’addizione: infatti la somma di due interi è un intero, l’addizione è associativa e commutativa, esiste l’elemento neutro additivo (lo zero) e per ogni intero a è definito il suo inverso additivo, che coincide con il suo opposto −a. Non è invece un gruppo l’insieme N dei numeri naturali rispetto all’addizione, in quanto non è definito l’inverso additivo: l’opposto di un numero naturale non nullo non è infatti un numero naturale.

Un gruppo moltiplicativo è un gruppo in cui l’operazione è formalmente trattata come una moltiplicazione (notazione moltiplicativa); solitamente, in questo caso l’operazione del gruppo è indicata con il simbolo ⋅ o spesso omessa, scrivendo consecutivamente gli elementi moltiplicati. Similmente un gruppo additivo è un gruppo in cui l’operazione è formalmente trattata come un’addizione (notazione additiva); in questo caso l’operazione del gruppo è solitamente indicata con il simbolo +. Se G è un gruppo moltiplicativo con operazione ⋅, allora, in analogia con il caso numerico, l’elemento

è indicato in modo compatto con il simbolo gⁿ; se invece G è un gruppo additivo con operazione +, allora, sempre in analogia con il caso numerico, l’elemento

è indicato in modo compatto con il simbolo ng, dove n è un arbitrario numero intero positivo. La differenza tra un gruppo moltiplicativo e un gruppo additivo è puramente notazionale. Ogni gruppo può essere equivalentemente trattato usando la notazione moltiplicativa o la notazione additiva: nelle due rispettive notazioni, gli elementi gⁿ e ng indicano lo stesso elemento. Sempre in analogia con il caso numerico, in un gruppo moltiplicativo l’elemento neutro è indicato con il simbolo 1, l’inverso di un elemento g è indicato con il simbolo g⁻¹ e si pongono per definizione le uguaglianze formali g⁰ = 1 e g⁻ⁿ = (gⁿ)⁻¹, dove n è un qualsiasi numero naturale. Similmente, in un gruppo additivo, l’elemento neutro è indicato con il simbolo 0, l’inverso di un elemento g è indicato con il simbolo −g e si pongono per definizione le uguaglianze formali 0g = 0 e (−n)g = −(ng), dove n è un qualsiasi numero naturale. Un sottogruppo H di un gruppo G(⋅) è un sottoinsieme H di G che risulta essere un gruppo rispetto alla stessa operazione definita in G: si scrive allora H ≤ G. L’insieme formato dal solo elemento neutro e il gruppo G stesso sono sottogruppi banali. Un particolare sottogruppo di G è il centro, indicato con il simbolo Z(G), definito come il sottoinsieme degli elementi di G che commutano con ogni altro elemento di G: Z(G) = {g ∈ G : g ⋅ h = h ⋅ g ∀g ∈ G}. G è detto finito se, come insieme, è costituito da un numero finito di elementi; altrimenti è detto infinito. L’ordine di G è la sua cardinalità come insieme. Se G è un gruppo finito, allora l’ordine di un sottogruppo H divide sempre l’ordine di G (teorema di Lagrange): il rapporto tra l’ordine di G e l’ordine di H è detto indice di H in G ed è usualmente indicato con il simbolo [G : H]. Un’importante conseguenza di questo fatto è che ogni elemento, elevato all’ordine di G, restituisce l’elemento neutro 1. Si definisce dunque l’ordine di un elemento g di G (indicato con ord(g)) come il minimo intero n tale che gⁿ = 1. Un’analoga definizione vale in un gruppo infinito: diversamente dal caso finito, però, in un gruppo infinito può non esistere alcun intero n per cui gⁿ = 1, nel qual caso si dice che l’elemento g ha ordine infinito.

Dato un sottogruppo H ≤ G, il sottoinsieme aH = {a ⋅ h}_h ∈ H formato dagli elementi di G che risultano il prodotto di un elemento a (fisso) di G per un elemento h (variabile) di H è detto classe laterale sinistra di G rispetto a H (o modulo H). Analogamente il sottoinsieme Ha = {h ⋅ a}_h ∈ H è detto classe laterale destra di G modulo H. Più sinteticamente si usa anche parlare di laterale sinistro e laterale destro. Due classi laterali sinistre (destre) modulo lo stesso sottogruppo o coincidono o sono disgiunte e pertanto le classi laterali sinistre (destre) modulo un sottogruppo H costituiscono una partizione di G, che è associata alla relazione di equivalenza per la quale due elementi sono in relazione se e solo se appartengono alla stessa classe laterale. Formalmente tale relazione ρ è così definita: x ρ y se e solo se x⁻¹ ⋅ y ∈ H. Nel contesto dei gruppi finiti, un’importante classe di esempi è costituita dagli insiemi → Z_n delle classi resto modulo un numero naturale n, dotati della struttura di gruppo rispetto all’addizione ereditata naturalmente dall’insieme Z dei numeri interi: essi sono tutti esempi di gruppi ciclici (→ gruppo ciclico) generati dalla classe [1], e il loro ordine coincide con il modulo n.

Ogni gruppo finito G di ordine n può essere definito mediante la propria tabella di → Cayley, vale a dire mediante una tabella, con n + 1 righe e n + 1 colonne in cui sono indicati tutti i risultati delle operazioni tra gli elementi del gruppo. Per esempio, l’insieme delle isometrie di un triangolo equilatero ABC in sé stesso è costituito dagli elementi

e forma un gruppo di ordine 6 rispetto all’operazione di composizione di trasformazioni ∘, che può essere così definito:

Dalla tabella si vede che il gruppo non è commutativo e che il sottoinsieme delle rotazioni ne costituisce un sottogruppo commutativo. Un secondo modo più compatto ed economico per definire un gruppo (eventualmente anche infinito) è quello di fornirne una presentazione, che consiste nell’esibizione di un insieme di generatori unita alle relazioni da essi soddisfatte. Importanti esempi di gruppi facilmente definibili tramite presentazione sono quelli che nascono come gruppi di isometrie di particolari figure geometriche piane: essi sono il gruppo di Klein V, definito dalla presentazione

(→ Klein, gruppo di), e più in generale i gruppi diedrali (→ gruppo diedrale), che per certi versi generalizzano il gruppo di Klein, definiti dalla presentazione (dove n ≥ 2 è un numero naturale)

L’esempio relativo al triangolo equilatero, riportato sopra in tabella, è il gruppo diedrale D₃ mentre il suo sottogruppo delle rotazioni è un gruppo ciclico.

Un gruppo si dice libero se ammette una presentazione priva di relazioni banali. Un gruppo, poi, si dice finitamente generato da un sottoinsieme S di G, e si scrive G = 〈S〉, se ogni suo elemento può essere ottenuto, a partire da S, eseguendo un numero opportuno di volte l’operazione definita nel gruppo e l’operazione di inverso sugli elementi di S.

Altri importanti esempi di gruppi sono costituiti dal → gruppo simmetrico S_n, definito come il gruppo delle permutazioni di un insieme costituito da n elementi (il precedente esempio, D₃, è anche gruppo simmetrico S₃), dai → gruppi classici di matrici, definiti come opportuni gruppi di trasformazioni di spazi vettoriali o proiettivi, e dai gruppi ciclici.

Gruppo quoziente (o gruppo fattore o gruppo complementare)

Struttura formata dalle classi che si determinano in un gruppo G definendo una relazione di equivalenza a partire da un suo sottogruppo normale. Un sottogruppo H di un gruppo G è detto sottogruppo normale, e si scrive H ⊲ G, se per ogni h ∈ H e ogni g ∈ G si ha g ⋅ h ⋅ g⁻¹ ∈ H. Se G è un gruppo e se H è un suo sottogruppo normale, allora si considera la relazione di equivalenza:

L’insieme delle classi di equivalenza rispetto a tale relazione eredita naturalmente l’operazione definita in G e acquisisce la struttura di gruppo: dotato di questa struttura, esso è detto il gruppo quoziente di G modulo H ed è indicato con il simbolo G /H. Per esempio, se G è il gruppo Z dei numeri interi rispetto all’addizione e se H è il sottogruppo generato da 3 (vale a dire il sottogruppo costituito dai multipli di 3), allora le classi di equivalenza coincidono con le classi resto modulo 3:

e il gruppo quoziente Z/H altri non è che Z₃ (si veda → Z_n, insieme delle classi resto modulo n).

Un gruppo privo di sottogruppi normali, diversi da quelli banali costituiti dal gruppo stesso e dal gruppo formato dall’elemento neutro, è detto gruppo semplice. In un gruppo abeliano tutti i sottogruppi sono normali.

Estensione di un gruppo

Dati due gruppi (G₁, +) e (G₂, ∘) è possibile estendere naturalmente uno dei due gruppi mediante l’altro gruppo in modo da formare un ulteriore gruppo, che è detto → prodotto diretto dei gruppi dati.

Gruppi risolubili

Un gruppo si dice risolubile se esiste un numero naturale n e una successione finita di sottogruppi G₀, G₁, …, G_n di G contenuti l’uno nell’altro, con G₀ uguale a G e con G_n uguale al gruppo banale costituito dal solo elemento neutro {e} = G_n ≤ ... ≤ G₁ ≤ G₀ = G, tali che ciascun sottogruppo è normale nel precedente e ogni gruppo quoziente G_i−1/G_i è un gruppo commutativo. Tali gruppi hanno un ruolo fondamentale nello studio della risolubilità per radicali di un’equazione algebrica in un’incognita (→ Galois, teoria di).

Gruppi ordinati

Se G(∘) è un gruppo dotato di un ordinamento ≤, allora l’ordinamento ≤ è detto compatibile con la struttura gruppale di G se, per arbitrari elementi x e y di G, è soddisfatta la condizione: se x ≤ y, allora ∀z ∈ G, x ∘ z ≤ y ∘ z. Un gruppo G dotato di un ordinamento compatibile è detto un gruppo ordinato. Per esempio, l’insieme dei numeri interi Z, come gruppo additivo, è un gruppo ordinato rispetto all’usuale ordinamento.