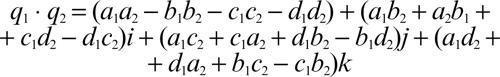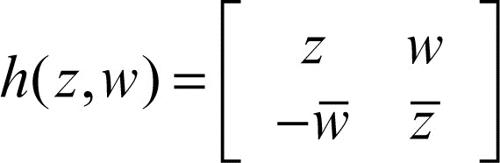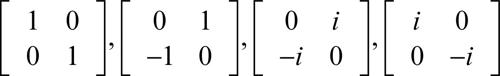H

H

H (insieme dei quaternioni) insieme introdotto nel 1843 da W.R. Hamilton nell’intento di estendere l’insieme C dei numeri complessi. Definiti infatti i numeri complessi come coppie ordinate di numeri reali, dotate come coppie delle usuali operazioni algebriche, appariva naturale considerare insiemi di terne, quaterne, …, n-ple qualunque che contenessero al loro interno R e C. Dopo numerosi tentativi, durati per un decennio, alla ricerca di un insieme numerico generato da tre unità di cui due immaginarie (1, i, j), che avrebbe rappresentato una naturale estensione alle tre dimensioni del piano di → Argand-Gauss, Hamilton si rese conto che, affinché questo ambiente fosse coerente con le operazioni in R e C, occorreva introdurre una quarta dimensione e inoltre non poteva più essere valida la proprietà commutativa. Fu così che inventò i quaternioni, numeri del tipo a + bi + cj + dk con a, b, c, d ∈ R.

L’insieme dei quaternioni, indicato con H in onore di Hamilton, è dotato di due operazioni di addizione e di moltiplicazione che estendono le medesime operazioni definite in C; non costituisce tuttavia un campo, in quanto la moltiplicazione tra quaternioni non è commutativa. Essendo soddisfatti tutti gli altri assiomi di campo, l’insieme H dei quaternioni possiede la struttura algebrica di corpo (non commutativo). Contemporaneamente, esso è uno spazio vettoriale di dimensione 4 sul campo R dei numeri reali; essendo inoltre lineare la moltiplicazione tra quaternioni, H acquisisce anche la struttura di algebra di divisione su R.

Come algebra, H è generato dalle quattro unità (1, i, j, k), la moltiplicazione tra le quali è definita dalla seguente tabella:

Un quaternione è dunque un elemento della forma a + bi + cj + dk. La moltiplicazione definita sugli elementi della base si estende per linearità a tutto lo spazio vettoriale H: se q₁ = a₁ + b₁i + c₁j + d₁k e q₂ = a₂ + b₂i + c₂j + d₂k sono due quaternioni, allora il loro prodotto è definito dalla formula

Dotato dell’addizione definita nello spazio vettoriale e del prodotto appena definito, H acquisisce la struttura di corpo, con unità 1 + 0i + 0j + 0k = 1. Tale corpo non è commutativo in quanto, come risulta dalla tabella, per esempio, i ⋅ j ≠ j ⋅ i. Gli elementi i, j e k sono detti unità immaginarie: essi generano un gruppo non commutativo di ordine 8, indicato con il simbolo Q e detto gruppo delle unità dei quaternioni: Q = {±1, ±i, ±j, ±k}.

Un quaternione della forma a + bi + cj + dk è detto reale se b = c = d = 0, vettoriale se a = 0. Se a = b = c = d = 0, il quaternione è detto quaternione nullo ed è l’elemento neutro dell’addizione definita in H. L’insieme dei numeri reali si identifica con l’insieme dei quaternioni reali, mentre quello dei numeri complessi si identifica con l’insieme dei quaternioni per cui c = d = 0; inoltre, le operazioni di addizione e moltiplicazione ristrette a tali insiemi coincidono con le usuali operazioni definite rispettivamente tra numeri reali e numeri complessi. In questo senso, quindi, H è un’estensione sia di R sia di C. Similmente al caso dei numeri complessi, se q = a + bi + cj + dk è un quaternione, si definiscono allora il suo coniugato come il quaternione

la sua norma come il numero reale non negativo

e il suo modulo come il numero reale

Un quaternione ha norma nulla se e solo se esso stesso è nullo; come nel caso dei numeri complessi, l’inverso moltiplicativo di un quaternione q è definito dalla formula

Due quaternioni q₁ e q₂ si dicono permutabili se commutano, vale a dire se q₁ ⋅ q₂ = q₂ ⋅ q₁. Un quaternione si dice centrale se è permutabile con ogni altro quaternione: l’insieme dei centrali costituisce il centro dell’insieme dei quaternioni. Poiché ogni numero reale è commutabile con ogni altro quaternione, l’insieme dei numeri reali R è contenuto nel centro di H. Questa proprietà definisce in effetti il corpo dei quaternioni: H è l’unico corpo non commutativo di dimensione finita sul campo R dei numeri reali il cui centro contiene R (teorema di Frobenius).

Una seconda possibile rappresentazione dei quaternioni si ottiene per mezzo di matrici 2 × 2 a coefficienti complessi: secondo tale descrizione, H viene a coincidere con le matrici della forma

dove z e w sono due arbitrari numeri complessi. L’isomorfismo tra l’insieme dei quaternioni H e l’insieme delle matrici di questa forma è descritto dalla corrispondenza q ↔ h(z, w), dove, se q = a + bi + cj + dk, i numeri complessi z e w sono definiti come z = a + di e w = b + ci.

Secondo tale corrispondenza, gli elementi 1, i, j, k sono rappresentati rispettivamente dalle matrici

mentre la norma di un quaternione coincide con il determinante della matrice associata.