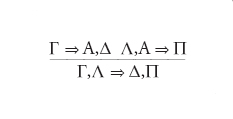Hauptsatz di Gentzen
Hauptsatz di Gentzen
Con questo nome (che significa teorema fondamentale) nella letteratura logica si indica una classe di teoremi il cui prototipo è dato dal risultato ottenuto da Gerhald Gentzen nel 1935 in base al quale – all’interno del calcolo classico dei sequenti LK per la logica elementare – ogni sequente dimostrabile Γ⇒Δ ha una dimostrazione che non utilizza la regola del taglio
Poiché la regola del taglio è l’unica del calcolo che comporta nella dimostrazione di un sequente Γ⇒Δ l’eventuale ricorso a formule che non compaiono come sottoformule di Γ⇒Δ, il teorema ha come corollario la validità del principio della sottoformula per cui ogni sequente in LK è dimostrabile utilizzando solo sottoformule delle formule che in esso compaiono. Un altro importante corollario – chiamato da Gentzen Hauptsatz esteso – afferma che ogni dimostrazione in LK si può trasformare in una dimostrazione in cui le applicazioni delle regole sui quantificatori seguono tutte le applicazioni delle regole sui connettivi. Il teorema si può estendere a logiche diverse da quella classica (per es., quella intuizionista LJ) e a teorie – non più calcoli logici – opportunamente formalizzate. La cosa è particolarmente importante nell’ambito del programma hilbertiano in quanto il principio della sottoformula ci garantisce immediatamente la coerenza e una dimostrazione finitista dell’Hauptsatz per queste teorie fornirebbe una dimostrazione finitista di coerenza. Come provato da Gentzen nel 1936 nel caso dell’aritmetica di Peano, il teorema vale ma richiede sul piano metateorico il ricorso all’induzione aperta sull’ordinale . Il discorso si può estendere a linguaggi più forti di quelli elementari e a teorie più potenti dell’aritmetica utilizzando principi metateorici – in particolare principi d’induzione o di recursione – che trascendono il punto di vista finitista ma conservano un qualche carattere costruttivo. Ricerche importanti in questo senso sono state svolte da Gaisi Takeuti, Kurt Schutte, William Tait, Jean-Yves Girard e altri. Su un altro versante, particolare interesse hanno riscosso negli ultimi decenni l’analisi di risultati come l’Hauptsatz nel contesto della teoria delle categorie.